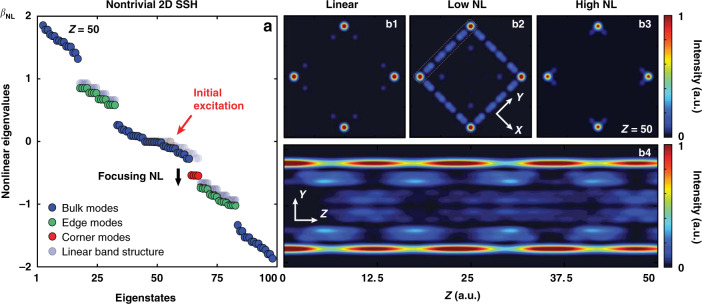
Fig. 2. Calculated nonlinear band structure and corner mode tuning under a self-focusing nonlinearity.
a Calculated nonlinear eigenvalues of the 2D SSH lattice βNL for the nontrivial lattice using the discrete model, where the transparent dots are linear modes superimposed for direct comparison. The black arrow shows that four corner states (red dots) undergo coupling and beating with lower edge states under low self-focusing nonlinearity (see also Supplementary video), and the red arrow marks the initially excited corner mode that sustains the topological feature under linear conditions as shown in b1 without any light distribution in the nearest neighboring sites. Under a low focusing nonlinearity, the corner mode couples with the edge modes (b2), and a beating oscillation occurs. This can be clearly seen from the side-view propagation of b4, taking from the upper-left edge marked by a dashed line in b2. Under a high focusing nonlinearity, a localized semi-infinite gap discrete soliton forms at the corners, with light distributing in the nearest neighboring sites (b3)