Abstract
Bayesian inference of phylogeny with Markov chain Monte Carlo plays a key role in the study of evolution. Yet, this method still suffers from a practical challenge identified more than two decades ago: designing tree topology proposals that efficiently sample tree spaces. In this article, I introduce the concept of adaptive tree proposals for unrooted topologies, that is, tree proposals adapting to the posterior distribution as it is estimated. I use this concept to elaborate two adaptive variants of existing proposals and an adaptive proposal based on a novel design philosophy in which the structure of the proposal is informed by the posterior distribution of trees. I investigate the performance of these proposals by first presenting a metric that captures the performance of each proposal within a mixture of proposals. Using this metric, I compare the performance of the adaptive proposals to the performance of standard and parsimony-guided proposals on 11 empirical data sets. Using adaptive proposals led to consistent performance gains and resulted in up to 18-fold increases in mixing efficiency and 6-fold increases in convergence rate without increasing the computational cost of these analyses. [Bayesian phylogenetic inference; Markov chain Monte Carlo; posterior probability distribution; tree proposals.]
Studies relying on Bayesian inference of phylogenies are routinely conducted with software packages designed specifically for this purpose (Yang and Rannala 1997, 2012). These packages implement the Markov chain Monte Carlo algorithm (MCMC) to estimate the posterior distribution of parameters of a model capturing the evolutionary history (phylogeny) of taxa and their mode of evolution. Despite the pervasiveness of these analyses, estimating such posterior distributions remains a computational challenge whose complexity largely stems from difficulties exploring and sampling the space of tree topologies.
The challenge of exploring tree space has been recognized since the earliest days of Bayesian phylogenetic inference (Huelsenbeck et al. 2001). Long analyses and failure to explore the region of high posterior probability was shown to be a common occurrence that increased in frequency with the number of taxa studied (Beiko et al. 2006). Data sets with large numbers of taxa frequently resulted in rugged posterior distributions where clusters of tree topologies with high posterior probabilities were separated by low-probability valleys. A decade ago, the use of the Metropolis-coupled MCMC algorithm (MC; Altekar et al. 2004) was proposed as a solution to this major issue. Although this solution is now considered as a standard practice, the settings required for this method to perform correctly remain a practical concern (Whidden and Matsen 2015; Brown and Thomson 2018). Using the MC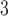 algorithm reduces the failure rate by easing the sampling of rugged posterior distributions of trees but does not significantly improve the sampling efficiency of the key actors for the exploration of the tree space: the tree proposals.
algorithm reduces the failure rate by easing the sampling of rugged posterior distributions of trees but does not significantly improve the sampling efficiency of the key actors for the exploration of the tree space: the tree proposals.
Only a limited number of studies have considered the challenge of defining efficient tree proposals. A thorough analysis of standard tree proposals was conducted by Lakner et al. (2008) who provided insight on their performance. Following this study, the concept of guided tree proposals was presented by Höhna and Drummond (2012). This important contribution suggested using scores (e.g., conditional clade probabilities or posterior probabilities) to bias the proposal toward the most promising trees among the set of trees proposed by a traditional tree proposal. However, the practicality of the resulting guided proposals remains limited due to the additional computational burden. These proposals were nonetheless implemented in MrBayes under the form of parsimony-guided proposals (Ronquist et al. 2012; Zhang et al. 2020).
Building efficient proposals for continuous parameters has been the subject of numerous studies in computational statistics (e.g., Gelman et al. 1996). These studies have led to the development of adaptive proposals. These proposals are self-tuned during an MCMC run to propose moves tailored specifically for the posterior distribution (Haario et al. 2001; Haario et al. 2005; Roberts and Rosenthal 2009). The field of computational phylogenetics has employed these approaches to improve the sampling efficiency of continuous parameters by designing novel adaptive proposals (Thawornwattana et al. 2017), developing multivariate proposals that exploit the correlation between parameters (Baele et al. 2017; Meyer et al. 2017), or by estimating distributions approximating the posterior distributions of specific parameters (e.g., branch lengths) to independently generate new parameter values (Aberer et al. 2015; Claywell et al. 2018). Most software for Bayesian inference of phylogeny takes advantage of these methods for continuous parameters (e.g., Ronquist et al. 2012; Aberer et al. 2014; Höhna et al. 2016; Baele et al. 2017). However, as no theory is readily available from the field of computational statistics regarding the sampling of tree topologies, none of this software implement adaptive proposals for tree topologies.
Software for Bayesian inference of phylogenies continues to mostly rely on tree proposals that naively explore the posterior distribution, as other alternatives are computationally expensive or impractical. The performance of these proposals hinders our ability to infer large phylogenies and to consider more complex and realistic evolutionary models. In this study, I present the theoretical foundations for the development of adaptive proposals for unrooted tree topologies and use them to develop three prototype adaptive proposals in the CoevRJ software (Meyer et al. 2019). The first two proposals are adaptive variants of commonly used proposals and the third proposal is a fully adaptive proposal based on a novel design philosophy. I investigate the computational complexity of these proposals and define a practical performance metric to assess the efficiency of each proposal within a mixture of proposals. Using this metric, I then study the practical performance of these proposals on simulated and empirical data sets, and compare it to the performance of traditional and parsimony-guided tree proposals.
Materials and Methods
Phylogenetic Tree Proposals
I consider the problem of developing efficient proposal kernels for unrooted tree topologies to conduct Bayesian inference of phylogeny. This type of analysis requires the estimation of the posterior probability distribution:
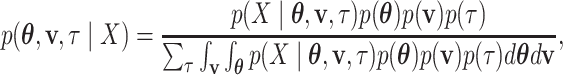 |
(1) |
with 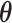 being the parameters of the evolutionary model,
being the parameters of the evolutionary model, 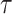 the unrooted tree topology,
the unrooted tree topology, 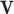 the branch lengths and
the branch lengths and 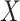 the alignment. Generally, the posterior distribution is estimated using the Metropolis–Hastings algorithm in which new parameters values are generated by a proposal kernel and accepted with probability
the alignment. Generally, the posterior distribution is estimated using the Metropolis–Hastings algorithm in which new parameters values are generated by a proposal kernel and accepted with probability
 |
(2) |
with 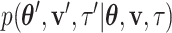 defining the probability with which the kernel proposes parameters
defining the probability with which the kernel proposes parameters 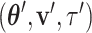 given
given 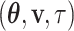 . In this study, I focus on proposal kernels modifying uniquely the tree topology and leaving the branch lengths invariant for the sake of simplicity (i.e.,
. In this study, I focus on proposal kernels modifying uniquely the tree topology and leaving the branch lengths invariant for the sake of simplicity (i.e., 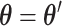 and
and 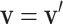 ), and on deriving their Hastings ratios having the form
), and on deriving their Hastings ratios having the form 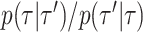 . Existing strategies to reassign branch lengths or hybrid proposals combining branch lengths and tree alterations are compatible with the tree proposals presented in this study (e.g., see Aberer et al. 2015 for mapping strategies or hybrid proposals).
. Existing strategies to reassign branch lengths or hybrid proposals combining branch lengths and tree alterations are compatible with the tree proposals presented in this study (e.g., see Aberer et al. 2015 for mapping strategies or hybrid proposals).
Common proposals employed for the inference of unrooted tree topologies include the stochastic Nearest Neighbor Interchange (stNNI), extending Subtree Pruning and Regrafting (eSPR; Swofford et al. 1996), and extending Tree Bisection and Reconnection (eTBR; Huelsenbeck et al. 2008). These proposals naively explore tree space by arbitrarily altering the current tree 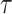 using subtree swapping or pruning operations. For instance, the stNNI proposal interchanges two subtrees separated by an internal branch, while the eSPR proposal prunes a subtree, moves it along a contiguous set of branches (a path), and finally regrafts it on the last branch of the path. Choices of branches, subtrees or paths are made randomly during these proposals and therefore frequently result in tree alterations with very low acceptance probability (e.g., removing a branch strongly supported by the data).
using subtree swapping or pruning operations. For instance, the stNNI proposal interchanges two subtrees separated by an internal branch, while the eSPR proposal prunes a subtree, moves it along a contiguous set of branches (a path), and finally regrafts it on the last branch of the path. Choices of branches, subtrees or paths are made randomly during these proposals and therefore frequently result in tree alterations with very low acceptance probability (e.g., removing a branch strongly supported by the data).
To improve the quality of the generated moves, adaptive proposals for continuous parameters use summary statistics of the posterior distribution, learned during an MCMC run, to tune the proposal mechanism (Roberts and Rosenthal 2009). Using these summary statistics, parameters of a proposal kernel (e.g., the scale of the random-walk) are adapted to target an optimal acceptance rate. While the specifics of such adaptive proposals are not directly applicable to tree topology proposals, the concept of using summary statistics of the posterior distribution can still be exploited. In this study, I use the estimated marginal posterior probabilities of splits, or split frequencies, to construct adaptive tree proposals. This strategy is based on two components: the estimation of the split frequencies and the design of adaptive proposals exploiting these estimates.
Split Frequencies
Each branch of a phylogenetic tree represents a unique bipartition of the set of taxa in the alignment. These bipartitions, better known as splits, are a useful tool to summarize the posterior distribution of trees. Using samples collected during an MCMC run, the marginal posterior probability of a split can be estimated by observing the frequency with which a given split occurs within the sampled tree topologies. Marginal split frequencies provide therefore inexpensive estimates of the support for each specific bipartition.
Adaptive tree proposals as defined in this study require the split frequencies to be learned and made available during MCMC runs. As in the post-MCMC estimation of the marginal split frequencies, this procedure is conducted by counting the occurrence of splits within the sampled tree topologies and normalizing them by the number of observed samples. This procedure guarantees that estimates of the split frequencies converge to the true posterior distribution when the MCMC algorithm is ergodic and run for an infinite amount of time. However, in practice, phylogenetic inferences are not run long enough to ensure the robustness and accuracy of the estimated split frequencies. To tackle this problem, I develop a heuristic algorithm to learn the split frequencies while overcoming several potential issues (Supplementary material available on Dryad at https://dx.doi.org/10.6078/D16D9P on learning split frequencies).
The first issue results from the bias induced by the starting parameters of the MCMC algorithm. The earliest phase of an MCMC run generally samples trees unrepresentative of the high probability region of the posterior distribution until equilibrium is reached. Therefore, in a postprocessing context, split frequencies are evaluated using samples remaining after the removal of the samples collected during the burnin phase. However, the duration of the burnin phase is unknown during an MCMC run and cannot be removed, so that estimated split frequencies might be biased by these early samples.
The second issue results from the volatility and oscillatory behavior of the estimated split frequency during the earliest phase, even after the equilibrium is reached. This oscillatory behavior depends on whether a split is present or absent in the sampled tree topology. Adaptive proposals constructed with these fluctuating estimates could induce unwanted dependencies between the proposal probabilities and the presence or absence of a split (e.g., nonreversibility of the proposals), and impact the correctness of the MCMC algorithm.
For these reasons, the heuristic learning algorithm is based on common practices used for adaptive proposals for continuous parameters (e.g., Haario et al. 1999; Andrieu and Thoms 2008). The algorithm averages the split frequencies over a fixed number of samples to reduce the volatility of the estimates, uses a relaxation mechanism that progressively reduces the impact of the earliest samples observed, and detects the convergence of the learning process when the amount of variation in split frequencies stabilizes. This convergence is further ensured by updating the estimated split frequencies using monotonic decreasing weights (i.e., strictly decreasing updates). Once convergence is reached, the learning process is terminated to ensure that the proposals preserve the ergodicity of the MCMC algorithm.
Adaptive proposals strongly rely on the estimated split frequencies. While this heuristic algorithm improves the robustness and accuracy of these estimates, it does not ensure a foolproof estimation procedure. Therefore, to further improve the robustness of adaptive proposals, these proposal mechanisms include a stochastic component 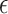 to ensure that all trees remain accessible regardless of the accuracy or correctness of the split frequency estimates (Supplementary material available on Dryad, stochastic component).
to ensure that all trees remain accessible regardless of the accuracy or correctness of the split frequency estimates (Supplementary material available on Dryad, stochastic component).
Adaptive Tree Proposals
Adaptive tree proposals rely on split frequencies to define regions of the tree that are weakly or strongly supported (i.e., having low or high split frequencies). These regions are used to define moves maintaining highly supported regions of the topology while proposing modifications to regions having weak support. For instance, applying this concept to the stNNI proposal could reduce the frequency of subtree swaps acting on splits with strong support while increasing the frequency of swaps acting on splits with weak support.
While this concept can be applied to build adaptive versions of naive proposals (e.g., stNNI or eSPR), two limitations to this approach must be accounted for. First, naive proposals generate relatively simple and specific tree alterations, and are computationally cheap. Their computational cost during an MCMC iteration is largely dominated by the cost of the resulting likelihood evaluation. To be efficient, adaptive versions of naive proposals must present a favorable trade-off between their inherent increase in computational cost and their enhanced sampling ability. However, these enhancements in sampling ability are limited by the simplicity and specificity of moves generated by naive proposals. Minimizing the increase in computational cost with respect to the cost of a likelihood evaluation is therefore key to designing competitive adaptive versions of naive tree proposals.
The second key limitation results from a more conceptual consideration: the type of moves generated by a tree proposal. In absence of native operations on the tree space, operators such as the nearest neighbor interchange (i.e., NNI), the tree bisection and reconnection (i.e., TBR), or the subtree regrafting and pruning (i.e., SPR) operators are used to manipulate tree topologies. Using these operators to define tree proposals such as the stNNI, eTBR, and eSPR proposals results in distinctive means of navigating the tree space (i.e., distinct types of moves). Since each analysis benefits differently from different types of moves, including tree proposals based on various operators in a mixture of proposals is fundamental to adequately explore the tree space (Lakner et al. 2008). Building adaptive variants of naive tree proposals limits the resulting proposals to generate distinct types of moves (e.g., NNI or TBR) and hinders their potential to adapt more broadly to different tree spaces.
To better understand why this approach might not be optimal for adaptive tree proposals, it is convenient to consider a graph-based representation of the tree space (Supplementary material available on Dryad, graph-based representation). In this representation, each vertex identifies a unique tree, and directed links (i.e., edges) represent the navigable network defined by a given operator. For instance, the NNI operator defines a network where only vertices representing trees reachable by swapping two subtrees separated by a single branch are linked. A naive tree proposal represents then a weighted version of these graphs where the network is defined by the operator and the link weights represent the probability of moving from a tree to another tree. Networks and link weights differ across naive proposals but remain fixed for each proposal during an MCMC analysis.
An adaptive version of a naive tree proposal will share the same network as its naive counterpart but will adapt the link weights (i.e., move probability) at runtime to favor moves leading to trees having high posterior probability using approximate split frequencies as a proxy score. While this adaptive-weights approach already represents an improvement over naive proposals, it fails to fully exploit the information contained in the split frequencies. This information can also be used to identify which links are more favorable out of extended networks that for instance consolidate networks of several types of moves.
Therefore, I propose here a different design philosophy where adaptive tree proposals use the split frequencies not only to adapt the link weights at runtime but also to pick which type of move is the most favorable out of an extended network. Similarly to eSPR and eTBR proposals, enumerating all outgoing links (i.e., moves) for a given vertex (i.e., tree) on such a network is impractical and expensive. Therefore, other move-building mechanisms analogous to the extension procedure of eSPR and eTBR proposals must be considered. In practice, this new concept of adaptive-network proposals uses split frequencies to identify weakly and strongly supported regions of a tree (e.g., clades or paths) that serve as building blocks for the proposed moves. This design philosophy allows adaptive tree proposals to generate tree alterations specifically tailored to fit the posterior distribution of tree topologies by tuning the link weights across an extended network including the networks of NNI, SPR, TBR operators, and more.
In this study, I consider both design philosophies for adaptive proposals. First, I define two adaptive-weights variants of existing naive proposals (stNNI and eSPR), that is proposals having a network constrained by a specific type of moves (i.e., NNI and SPR, respectively). Then, I present a novel adaptive-network proposal that uses the split frequencies to adaptively define the most favorable type of moves among those defined by an extended network.
Mathematical Notation
I use the following mathematical notation to describe adaptive proposals (summarized in Table 1): an unrooted tree topology 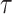 is defined by a set of vertices,
is defined by a set of vertices, 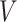 , and a set of edges, or branches,
, and a set of edges, or branches, 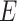 . The subset of edges,
. The subset of edges, 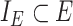 , identifies the set of internal edges. Each edge
, identifies the set of internal edges. Each edge 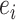 identifies a split
identifies a split 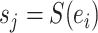 whose frequency is estimated by the function
whose frequency is estimated by the function 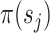 . A split
. A split 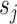 identifies a unique bipartition of the set of taxa and can therefore be identified differently in several tree topologies. For instance, two edges in different trees (e.g.,
identifies a unique bipartition of the set of taxa and can therefore be identified differently in several tree topologies. For instance, two edges in different trees (e.g., 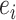 in
in 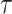 and
and 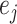 in
in 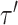 ) can identify the same split
) can identify the same split 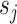 .
.
Table 1.
Mathematical notation.
| Variables | Interpretation |
|---|---|
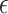
|
Stochastic component |
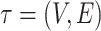
|
Unrooted tree topology with edges 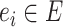 and vertices and vertices 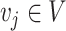
|
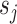
|
A unique split identified by 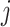 in the set of all possible splits in the set of all possible splits |
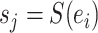
|
Operator returning the split identified by edge 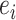
|
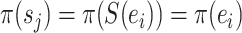
|
Operator returning the split frequency of 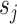
|
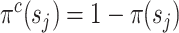
|
Complement of the split frequency |
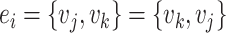
|
Undirected edges |
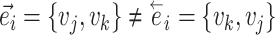
|
Directed edges |
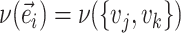
|
Internal edges contiguous to 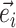 (neighboring edges) (neighboring edges) |
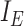
|
Set of internal edges |
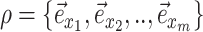
|
Contiguous path in the tree |
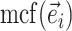
|
Min. split frequency in clade identified by edge 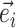
|
I use a flexible definition of splits in the sense that a split can be used to identify a bipartition and also to build new partitions. In the context of a move, a directed edge 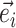 specifies the direction of operations involving this edge. For instance, the split
specifies the direction of operations involving this edge. For instance, the split 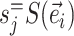 identifies the taxa in the clade subtended by edge
identifies the taxa in the clade subtended by edge 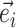 . Using this definition, a new split can then be constructed when a clade is moved by considering the union of two splits: for instance,
. Using this definition, a new split can then be constructed when a clade is moved by considering the union of two splits: for instance, 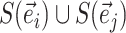 would identify a bipartition segregating the taxa in the clade subtended by edges
would identify a bipartition segregating the taxa in the clade subtended by edges 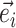 and
and 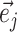 from all the other taxa.
from all the other taxa.
Edges contiguous to edge 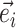 are identified by the operator
are identified by the operator 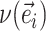 that returns the next edges according to the direction of
that returns the next edges according to the direction of 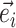 . As most of the adaptive proposals considered act on internal edges, the
. As most of the adaptive proposals considered act on internal edges, the 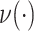 operator only returns edges contained in
operator only returns edges contained in 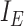 . Regions of the tree topology are identified by contiguous paths
. Regions of the tree topology are identified by contiguous paths 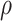 composed of a set of contiguous undirected or directed edges (e.g.,
composed of a set of contiguous undirected or directed edges (e.g., 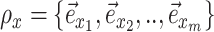 ). Lastly, the operator
). Lastly, the operator 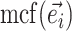 returns the smallest split frequency of the internal edges existing in the clade subtended by edge
returns the smallest split frequency of the internal edges existing in the clade subtended by edge 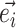 .
.
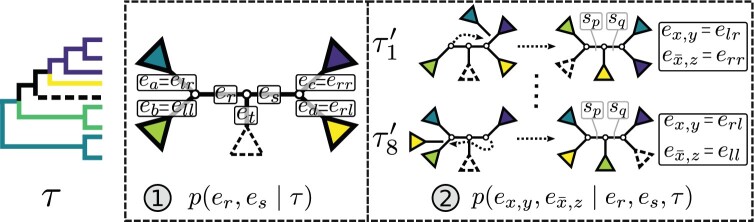
Adaptive stNNI
The adaptive stNNI (A-stNNI) proposal uses the split frequencies to guide the selection of the central edge 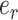 (Fig. 1). The split identified by this edge
(Fig. 1). The split identified by this edge 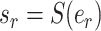 will be altered by the interchange of two subtrees located on each extremity of
will be altered by the interchange of two subtrees located on each extremity of 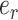 . The interchange to apply among the two possible outcomes is also guided by the split frequencies.
. The interchange to apply among the two possible outcomes is also guided by the split frequencies.
Figure 1.
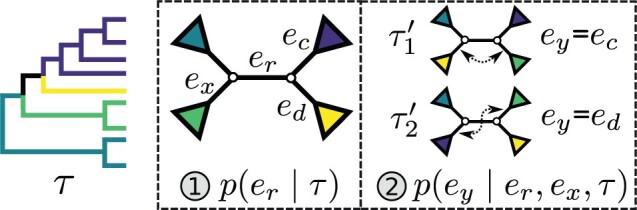
Steps of the A-stNNI proposal. In step 1, edge 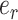 is selected according to Equation (3). Then, in step 2, the two subtrees to swap are selected according to Equation (4).
is selected according to Equation (3). Then, in step 2, the two subtrees to swap are selected according to Equation (4).
The selection of the central edge 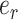 is biased toward edges identifying weakly supported splits. The central edge
is biased toward edges identifying weakly supported splits. The central edge 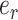 is selected with probability
is selected with probability
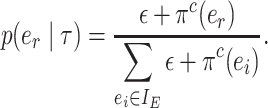 |
(3) |
The new split 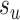 replacing
replacing 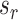 is determined by one of the two possible outcomes of subtree interchange. The edge
is determined by one of the two possible outcomes of subtree interchange. The edge 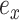 subtending the first subtree to swap is arbitrarily chosen among the four edges contiguous to edge
subtending the first subtree to swap is arbitrarily chosen among the four edges contiguous to edge 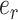 (i.e., with probability
(i.e., with probability 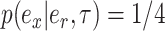 ). The second subtree is selected among the two subtrees on the opposite side of
). The second subtree is selected among the two subtrees on the opposite side of 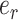 that are identified by edges
that are identified by edges 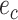 and
and 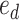 , respectively (Fig. 1). The new split
, respectively (Fig. 1). The new split 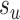 segregates the taxa identified by the edge
segregates the taxa identified by the edge 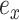 and either edge
and either edge 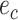 or
or 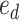 from the others, resulting in split
from the others, resulting in split 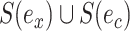 or
or 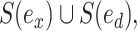 respectively. To favor the interchange leading to the tree with the strongest support, the edge
respectively. To favor the interchange leading to the tree with the strongest support, the edge 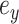 identifying the second subtree is selected with probability proportional to
identifying the second subtree is selected with probability proportional to 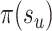 :
:
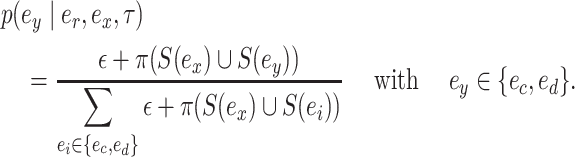 |
(4) |
An A-stNNI move is identified by the triplet of edges 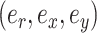 and is proposed according to probability
and is proposed according to probability
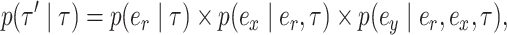 |
(5) |
and leads to the new tree topology  . The reverse move happens with probability
. The reverse move happens with probability
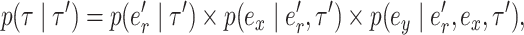 |
(6) |
where 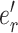 identifies the edge of the new split
identifies the edge of the new split 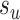 (i.e., central edge) in
(i.e., central edge) in 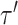 , and edges
, and edges 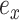 and
and 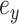 identify the same splits in
identify the same splits in 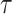 and
and 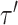 . The Hastings ratio required to evaluate the acceptance probability of a A-stNNI move (Eq. (2)) is the ratio of Equations (6) and (5).
. The Hastings ratio required to evaluate the acceptance probability of a A-stNNI move (Eq. (2)) is the ratio of Equations (6) and (5).
Adaptive 2-edges SPR
The adaptive 2-edges SPR (A-2SPR) is an adaptive version of the eSPR move. Similarly to the eSPR proposal, this adaptive proposal prunes a subtree, moves it along a path made of consecutive edges, and regrafts it (Fig. 2). The length of the path is however limited to exactly two edges, resulting in the alteration of two splits. In contrast to the usual eSPR strategy, the A-2SPR first selects the path along which the subtree will be moved and then considers all the possible pruning and regrafting moves along this path. The A-2SPR can be seen as a natural extension of the A-stNNI to two edges since the path is selected to target regions of the tree with weak support, while the move is selected to favor the resulting tree having the strongest support.
Figure 2.
Steps of the A-2SPR proposal. In step 1, the edges 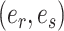 , along which a subtree will be moved, are selected according to Equation (7). Then, in step 2, a move among the 8 possible pruning and regrafting locations along edges
, along which a subtree will be moved, are selected according to Equation (7). Then, in step 2, a move among the 8 possible pruning and regrafting locations along edges 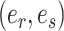 is selected according to Equation (8). Splits
is selected according to Equation (8). Splits 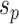 and
and 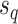 are identified on the resulting tree and correspond to terms
are identified on the resulting tree and correspond to terms 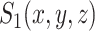 and
and 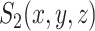 of Equation (8), respectively.
of Equation (8), respectively.
In the first step, I select a pair of contiguous edges 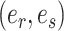 with probability inversely proportional to the product of their estimated marginal split frequencies, as defined by,
with probability inversely proportional to the product of their estimated marginal split frequencies, as defined by,
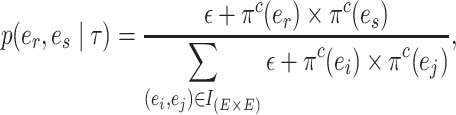 |
(7) |
where 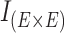 identifies the set containing all pairs of contiguous internal edges in
identifies the set containing all pairs of contiguous internal edges in 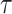 . The pair
. The pair 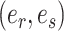 has the four edges
has the four edges 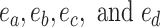 at its extremities and the edge
at its extremities and the edge 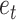 in its center, which is the edge sharing a vertex with both edges
in its center, which is the edge sharing a vertex with both edges 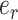 and
and 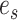 .
.
The second step enumerates all the possible moves across edges 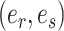 for subtrees subtended by edges
for subtrees subtended by edges 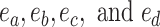 . Each of those edges can be regrafted two ways after moving along edges
. Each of those edges can be regrafted two ways after moving along edges 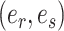 . For instance, assuming that
. For instance, assuming that 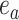 and
and 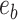 are adjacent, the subtree identified by edge
are adjacent, the subtree identified by edge 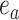 could be pruned and then regrafted on edges
could be pruned and then regrafted on edges 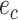 or
or 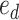 . Assuming that edge
. Assuming that edge 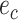 is selected as the regrafting point, the split
is selected as the regrafting point, the split 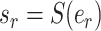 and
and 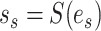 would be removed and would be replaced by splits
would be removed and would be replaced by splits  and
and  . The split
. The split 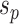 would separate taxa in subtrees identified by edges
would separate taxa in subtrees identified by edges 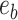 and
and 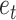 from the others (i.e.,
from the others (i.e., 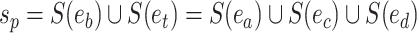 ), while the split
), while the split 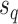 would separate taxa in the clade identified by edges
would separate taxa in the clade identified by edges 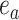 and
and 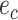 from the others (i.e.,
from the others (i.e., 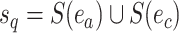 ).
).
For mathematical convenience, edges 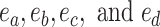 can be relabeled using their relative position using notation
can be relabeled using their relative position using notation 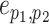 (Fig. 2). Indexes
(Fig. 2). Indexes 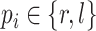 define whether the edges are at the right (
define whether the edges are at the right (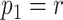 ) or left (
) or left (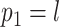 ) extremity of edges
) extremity of edges 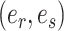 and whether the edges are the right or left one relative to each other (
and whether the edges are the right or left one relative to each other ( ). Using this notation, the subtree to prune is identified by its subtending edge
). Using this notation, the subtree to prune is identified by its subtending edge 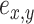 at extremity
at extremity 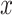 of edges
of edges 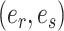 and the regrafting point is identified by edge
and the regrafting point is identified by edge 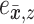 at the opposite extremity
at the opposite extremity 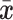 (e.g.,
(e.g., 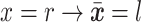 ). To propose favorable moves, the probability of selecting a pair of pruning and regrafing edges is proportional to the estimated marginal frequencies of the new resulting splits (i.e.,
). To propose favorable moves, the probability of selecting a pair of pruning and regrafing edges is proportional to the estimated marginal frequencies of the new resulting splits (i.e., 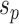 and
and 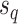 ) and is defined as
) and is defined as
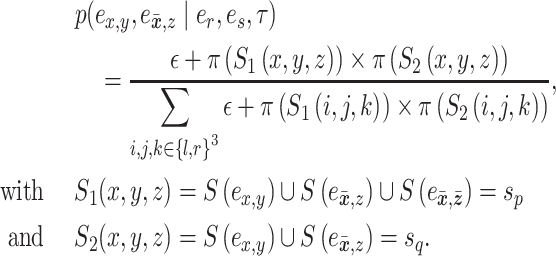 |
(8) |
The move identified by the quadruplet of edges 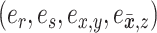 is proposed according to probability
is proposed according to probability
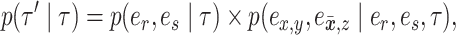 |
(9) |
and leads to the new tree topology 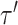 . The reverse move happens with probability
. The reverse move happens with probability
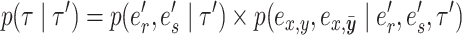 |
(10) |
where edges 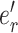 and
and 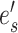 identify the new splits. Edge
identify the new splits. Edge 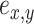 identifies the edge originally pruned and
identifies the edge originally pruned and 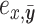 its neighbor in
its neighbor in 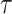 that subtend the same subtrees in
that subtend the same subtrees in 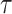 and
and 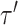 . The ratio of Equations (10) and (9) defines the Hastings ratio for the A-2SPR proposal that is used to evaluate the acceptance probability of a move (Eq. (2)).
. The ratio of Equations (10) and (9) defines the Hastings ratio for the A-2SPR proposal that is used to evaluate the acceptance probability of a move (Eq. (2)).
This strategy can be generalized to build adaptive N-edges SPR moves. However, two pitfalls are inherent to this approach. First, building proposals affecting a fixed number of edges, which includes the A-2SPR proposal, is inconvenient and can result in nonergodic proposals when used on their own. Second, the proposal’s efficiency would suffer from significant increases in computational cost. The computational complexity of the enumeration of all 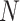 -edges paths grows as
-edges paths grows as 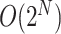 , while the one of estimating the move probabilities grows as
, while the one of estimating the move probabilities grows as 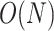 (Supplementary material available on Dryad, computational complexity).
(Supplementary material available on Dryad, computational complexity).
Adaptive Path Building and Jolting Proposal
While the A-stNNI and A-2SPR proposals generate moves constrained by the NNI and SPR move types (i.e., fixed network), the adaptive path building and jolting proposal (A-PBJ) embraces a different design philosophy that uses the estimated split frequencies to define the move type adaptively (i.e., adaptive-network proposal). This approach is achieved by using the split frequencies to identify two types of structures within a tree topology: weakly and strongly supported regions. A proposal designed under this philosophy will strive to generate moves maintaining the regions with strong support while altering other regions with weak support. Moves resulting from this strategy are specifically tailored to fit the posterior distribution of trees at hand.
The A-PBJ proposal implements this novel design philosophy by using contiguous paths within a tree to identify weakly and strongly supported regions: the unstable and stable paths, respectively (Fig. 3). The procedure used to build such paths and an A-PBJ move are first summarized here and then detailed in the next sections, and lastly illustrated with an example in the Supplementary material available on Dryad (Path building: an illustrative example).
Figure 3.
Schematic of an A-PBJ proposal. The two SPR-type moves defined by the stable path 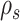 (Fig. 4) and unstable paths
(Fig. 4) and unstable paths 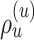 and
and 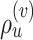 (Fig. 5) are applied on the example tree
(Fig. 5) are applied on the example tree 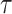 , resulting in tree
, resulting in tree 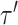 . After having defined a stable path and two unstable paths (step 1), the two SPR-type moves identified by their respective unstable paths consist of pruning the clade including the stable path (step 2) and then regrafting it at the opposite extremity of their respective unstable paths (step 3). The probability of an A-PBJ move is the joint probability of building the stable path and the two unstable paths as defined in Equations (11) and (12).
. After having defined a stable path and two unstable paths (step 1), the two SPR-type moves identified by their respective unstable paths consist of pruning the clade including the stable path (step 2) and then regrafting it at the opposite extremity of their respective unstable paths (step 3). The probability of an A-PBJ move is the joint probability of building the stable path and the two unstable paths as defined in Equations (11) and (12).
This proposal begins by selecting a stable path acting as the backbone of the move. Unstable paths are then constructed at both extremities of the backbone when possible: that is, when the stable path leads to internal edges (Fig. 3, step 1). An unstable path defines an eSPR-type move by construction. First, the edge at the extremity of the stable path and adjacent to the unstable path is pruned (Fig. 3, step 2). The subclade including the backbone is moved along the unstable path and then regrafted (Fig. 3, step 3).
The stable path and its splits remain unaltered by this move, while the splits of both unstable paths are replaced by new splits. Depending on the number of unstable paths identified and the edges forming them, move types produced by the A-PBJ proposal include, but are not limited to, stNNI, eSPR, and eTBR moves. For instance, if only one unstable path composed of one edge can be built, then the A-PBJ proposal generates a single 1-step SPR-type move or equivalently a stNNI-type move. However, if two unstable paths are built and include several edges, then the move generated by the A-PBJ proposal is equivalent to an eTBR-type move if the stable path has only one edge or a pair of independent eSPR-type moves otherwise.
The path building strategies are key to the efficiency and reliability of the A-PBJ proposal. The stable paths must capture sets of splits having high frequencies that would benefit from alterations at their extremities; constructing stable paths starting and ending at terminal nodes would not enable any moves. The unstable paths must capture sets of low-frequencies splits of variable size and, in this sense, act as a generalization of the mechanisms previously employed in the A-stNNI and A-2SPR. This generalization must, however, avoid the expensive enumeration of all possible N-edges paths to remain computationally competitive.
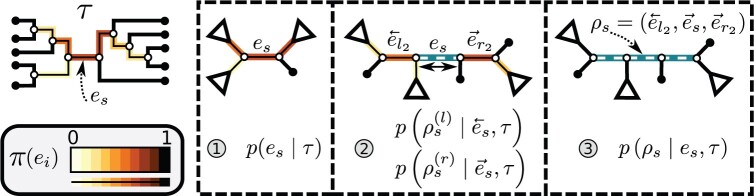
The strategies used to construct such paths and their resulting probabilities are defined in the following sections. The construction of a stable path 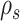 with probability
with probability 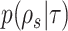 is illustrated in Figure 4. The unstable paths
is illustrated in Figure 4. The unstable paths 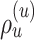 and
and 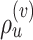 are built at each extremity of the stable path
are built at each extremity of the stable path 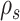 identified by edges
identified by edges 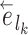 and
and 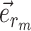 . Those unstable paths are constructed with probabilities
. Those unstable paths are constructed with probabilities 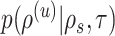 and
and 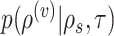 , respectively, as illustrated in Figure 5.
, respectively, as illustrated in Figure 5.
Figure 4.
Construction of a stable path 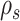 using split frequencies
using split frequencies 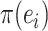 . In step 1, the edge
. In step 1, the edge 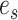 is selected according to Equation (13). Then, in step 2, the path is extended on both sides of edge
is selected according to Equation (13). Then, in step 2, the path is extended on both sides of edge 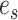 according to Eqs. (14–16). Finally, in step 3, both extensions are concatenated forming path
according to Eqs. (14–16). Finally, in step 3, both extensions are concatenated forming path 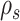 (Eqs. 17–19)). Edges of the stable path are represented with dashed white lines. Other edges are represented with solid black lines and colored in function of their split frequency.
(Eqs. 17–19)). Edges of the stable path are represented with dashed white lines. Other edges are represented with solid black lines and colored in function of their split frequency.
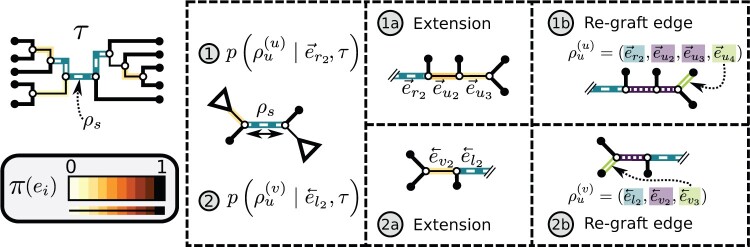
Figure 5.
Construction of the unstable paths 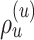 and
and 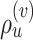 at the extremities of
at the extremities of 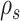 (Fig. 4). In the two separate building phase (steps 1 and 2), the paths are constructed by extension (steps 1a and 2a) according to Eqs. ((20)–(22)). Then, the last edges identifying the re-graft points (steps 1b and 2b) are selected according to Eq. (23). In steps 1b and 2b, the edges identifying the clades to prune, the paths and the regrating points are represented with dashed, dotted and solid white lines, respectively. Other edges are represented with solid black lines and colored in function of their split frequency.
(Fig. 4). In the two separate building phase (steps 1 and 2), the paths are constructed by extension (steps 1a and 2a) according to Eqs. ((20)–(22)). Then, the last edges identifying the re-graft points (steps 1b and 2b) are selected according to Eq. (23). In steps 1b and 2b, the edges identifying the clades to prune, the paths and the regrating points are represented with dashed, dotted and solid white lines, respectively. Other edges are represented with solid black lines and colored in function of their split frequency.
The probability of an A-PBJ move is defined using the joint probability of building its component paths and is given as
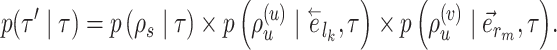 |
(11) |
The reverse move happens with probability
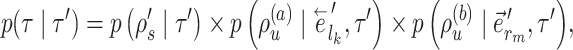 |
(12) |
where 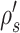 identifies the path including edges identifying the same splits as
identifies the path including edges identifying the same splits as 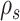 . Paths
. Paths 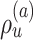 and
and 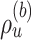 are inverse versions of path
are inverse versions of path 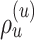 and
and 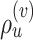 , respectively, and identify the reverse eSPR-type moves.
, respectively, and identify the reverse eSPR-type moves.
The ratio of Equations (12) and (11) defines the Hastings ratio for the A-PBJ proposal required to evaluate the acceptance proposal of a move (Eq. (2)). The different terms involved in Equations (11) and (12) are detailed in the next sections.
Stable Path
The construction of a stable path 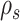 involves first selecting an edge with probability
involves first selecting an edge with probability
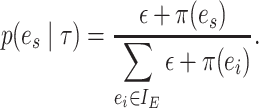 |
(13) |
This equation favors the selection of edges identifying high-frequency splits. The path  is then built by step-wise extension of its extremities. Starting from edge
is then built by step-wise extension of its extremities. Starting from edge  the path is extended in both directions, namely the
the path is extended in both directions, namely the 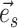 and
and 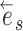 directions, respectively (Fig. 4, step 2). After including edge
directions, respectively (Fig. 4, step 2). After including edge 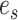 in a partial path (e.g.,
in a partial path (e.g., 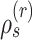 ), the extension mechanism iterates over two steps: first, the termination condition of the extension, and second (if not terminated), the extension of the path with a new edge.
), the extension mechanism iterates over two steps: first, the termination condition of the extension, and second (if not terminated), the extension of the path with a new edge.
Assuming an initial direction 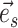 and the initial partial path
and the initial partial path 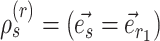 , the first iteration (
, the first iteration ( ) begins by testing the termination condition that occurs with probability
) begins by testing the termination condition that occurs with probability
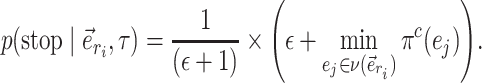 |
(14) |
This probability favors the termination of the extension mechanism whenever a split identified by a neighboring internal edge 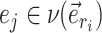 could benefit from being altered. However, when edge
could benefit from being altered. However, when edge 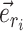 does not lead to at least one internal neighboring edge (i.e.,
does not lead to at least one internal neighboring edge (i.e., 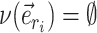 ), then the extension terminates deterministically.
), then the extension terminates deterministically.
If the termination condition is not met (which happens with probability 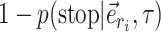 ) and the next candidate edges are not terminal, the path continues its extension by selecting the next edge to add. Internal edges identifying a split with high frequency and leading to a clade containing low-frequency structures represent good candidates for extension and are selected with probability
) and the next candidate edges are not terminal, the path continues its extension by selecting the next edge to add. Internal edges identifying a split with high frequency and leading to a clade containing low-frequency structures represent good candidates for extension and are selected with probability
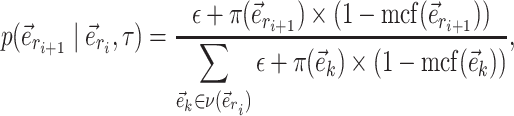 |
(15) |
where 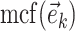 identifies the minimum split frequency in the clade identified by
identifies the minimum split frequency in the clade identified by  . The selected edge
. The selected edge  is then added to the path (e.g.,
is then added to the path (e.g., 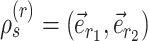 ) and a new iteration begins (
) and a new iteration begins ( ).
).
This process continues until the termination event occurs or until the path reaches an endpoint (i.e.,  ) . The probability of having extended the partial stable path
) . The probability of having extended the partial stable path 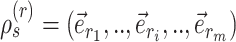 in direction
in direction 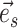 is then given as
is then given as
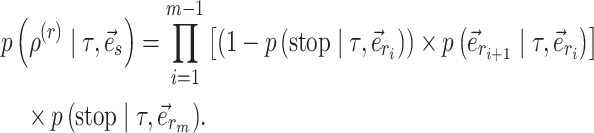 |
(16) |
The extension mechanism is repeated in the opposite direction (i.e., 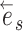 ) resulting in partial stable path
) resulting in partial stable path 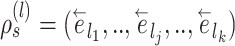 . Both partial paths
. Both partial paths 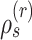 and
and 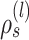 are then concatenated to form the stable path
are then concatenated to form the stable path
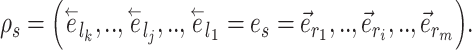 |
(17) |
The construction of this path is conditional on the selection of edge 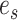 as starting point and is built with probability
as starting point and is built with probability
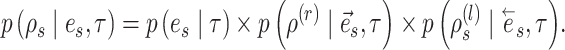 |
(18) |
Given that this exact path may be built starting from any edge 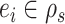 , the probability of building path
, the probability of building path 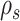 must be marginalized over all potential starting edges and is defined as
must be marginalized over all potential starting edges and is defined as
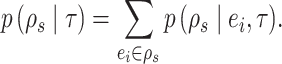 |
(19) |
Unstable Paths
The mechanism used to build unstable paths consists of extension phases starting from each of the extremities of the stable path 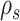 , each identified by edges
, each identified by edges 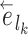 and
and 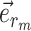 , respectively. An unstable path fully defines an eSPR-type move (Fig. 5). For instance, the unstable path
, respectively. An unstable path fully defines an eSPR-type move (Fig. 5). For instance, the unstable path 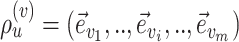 starting after edge
starting after edge 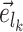 includes the edge to prune (
includes the edge to prune (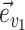 ) that subtends the moving clade
) that subtends the moving clade  (i.e., the clade containing the stable path), the edge that identifies the direction of the move (
(i.e., the clade containing the stable path), the edge that identifies the direction of the move (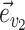 ), the edges traversed by clade
), the edges traversed by clade 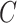 and the regrafting point of clade
and the regrafting point of clade 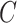 (
(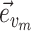 ). As in the extension of the stable path, an unstable path
). As in the extension of the stable path, an unstable path 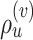 is built by iterating over two steps: the extension termination and edge selection steps.
is built by iterating over two steps: the extension termination and edge selection steps.
The extension phase is terminated with a probability proportional to the risk of extending the unstable path with an edge identifying a split with a high-frequency in the next step. The termination event occurs with probability
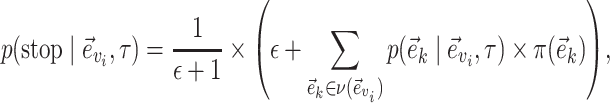 |
(20) |
where 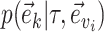 is the probability of extending path
is the probability of extending path 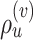 with edge
with edge 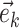 (Eqs. (21–23)). When edge
(Eqs. (21–23)). When edge 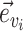 does not lead to at least one internal neighboring edge (i.e.,
does not lead to at least one internal neighboring edge (i.e., 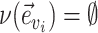 ), then the extension terminates deterministically.
), then the extension terminates deterministically.
If the termination does not occur, the next edge is selected according to probabilities defined by the edge’s role in the eSPR move (i.e., direction, traversed or regrafting edge). The first edge selected identifies the direction along which clade  will move and is selected with probability
will move and is selected with probability
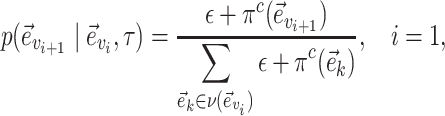 |
(21) |
that favors the removal of edges identifying low-frequency splits.
Each edge traversed by clade 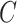 is then selected with probability
is then selected with probability
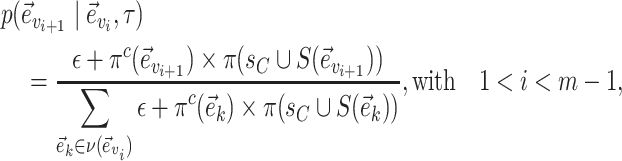 |
(22) |
where 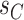 identifies the split containing the taxa of clade
identifies the split containing the taxa of clade 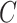 . This probability accounts for the removal of the current split
. This probability accounts for the removal of the current split 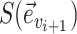 and the addition of the new split
and the addition of the new split 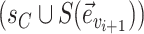 .
.
The last edge, selected after the termination of the extension phase, identifies the regrafting edge for clade 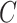 and is selected with probability
and is selected with probability
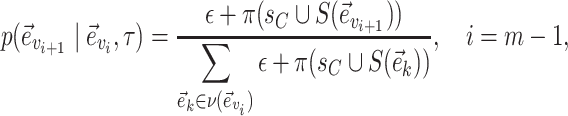 |
(23) |
that is, in proportion to the frequency of the last split added.
Building an unstable path 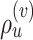 is the outcome of the selection of the direction, the extension of the traversed path and the choice of the regrafting edge. The probability of building an unstable path is therefore defined as,
is the outcome of the selection of the direction, the extension of the traversed path and the choice of the regrafting edge. The probability of building an unstable path is therefore defined as,
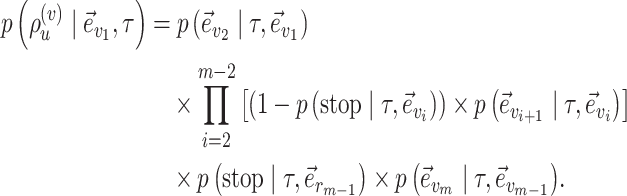 |
(24) |
The probability of an A-PBJ move (Eqs (11) and (12)) is defined as the joint probability of building a stable path (Eq (19)) and the two unstable paths starting at its extremities (Eq (24)).
Parsimony-Guided stNNI and eSPR
I implemented parsimony-guided stNNI and eSPR proposals based on the concepts presented in Höhna and Drummond (2012) to compare adaptive proposals with other strategies for guiding tree proposals (Supplementary material available on Dryad, Parsimony score transformation). Two different strategies were considered: exhaustive guided stNNI (G-stNNI) and guided N-edges eSPR (G-NSPR) proposals. The mechanism of these proposals consists of defining a set of potential moves and drawing one of them proportionally to the parsimony score of the resulting trees. Each proposal differs in the strategy used to build the set of moves. The G-stNNI proposal enumerates all possible stNNI moves for the current tree  . The G-NSPR proposal randomly choose a subtree to prune, then enumerates all eSPR moves altering at most N-edges. Using
. The G-NSPR proposal randomly choose a subtree to prune, then enumerates all eSPR moves altering at most N-edges. Using  has a similar effect to a guided stNNI that would randomly choose the central edge and then use the parsimony score to guide the subtree interchange.
has a similar effect to a guided stNNI that would randomly choose the central edge and then use the parsimony score to guide the subtree interchange.
Theoretical Computational Complexity of Proposals
The performance of an MCMC proposal is defined by its sampling efficiency and its computational cost relative to the likelihood evaluation. Understanding how the computational cost of tree proposals grows with respect to different data set sizes or model complexity is therefore important to identify potential limitations. Since, it is not practically possible to test several tree proposals on a broad range of data sets and models, I defined the theoretical computational complexity of the different proposals used in this study and compared them to the cost of a partial likelihood (Supplementary material available on Dryad, computational complexity). These complexities and the conditions under which a proposal is strictly less expensive than a partial likelihood evaluation are summarized in Table 2. This theoretical analysis indicates that parsimony-guided tree proposals have performance improvements limited by their dependencies to the number of sites 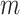 . Conversely, adaptive tree proposals should have negligible computational cost as long as the number of taxa
. Conversely, adaptive tree proposals should have negligible computational cost as long as the number of taxa 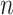 is smaller than
is smaller than 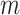 .
.
Table 2.
Computational complexity of the proposals, likelihood operations and condition under which a proposal is strictly less expensive than a likelihood evaluation (i.e., Cost condition).
| Operation | Complexity | Cost condition |
|---|---|---|
| Full lik. |
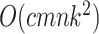
|
— |
| Partial lik. |
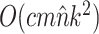
|
— |
| Partial pars. |
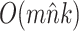
|
— |
| stNNI |
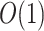
|
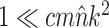
|
| eSPR |
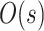
|
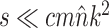
|
| eTBR |
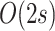
|
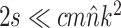
|
| G-stNNI |
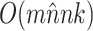
|
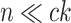
|
| G-NSPR |
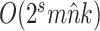
|
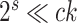
|
| A-stNNI |
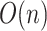
|
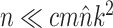
|
| A-2SPR |
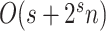
|
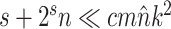
|
| A-PBJ |
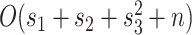
|
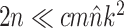
|

|
Notes: Alignments have 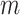 sites for
sites for 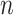 sequences defined over an alphabet of
sequences defined over an alphabet of 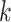 characters (e.g.,
characters (e.g., 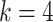 for nucleotide sequences). The Gamma model for rate heterogeneity has a number
for nucleotide sequences). The Gamma model for rate heterogeneity has a number 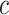 of rate categories (Yang 1994), while a partial likelihood requires
of rate categories (Yang 1994), while a partial likelihood requires 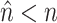 operations instead of
operations instead of 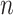 . Finally,
. Finally, 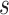 represents the number of splits altered by a move. For the A-PBJ proposal,
represents the number of splits altered by a move. For the A-PBJ proposal, 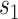 ,
, 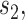 and
and 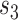 identify the number of edges in the two unstable paths and stable path, respectively.
identify the number of edges in the two unstable paths and stable path, respectively.
The parsimony-guided proposal G-stNNI could exceed the computational complexity of a partial likelihood evaluation under the condition that the number of taxa 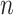 exceed the product of the number of symbols
exceed the product of the number of symbols 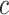 (e.g.,
(e.g., 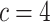 for nucleotides) and the number of rate categories
for nucleotides) and the number of rate categories 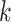 under a discrete-Gamma rate model (Yang 1994). Such scenarios would happen even when using moderately complex models as the GTR+
under a discrete-Gamma rate model (Yang 1994). Such scenarios would happen even when using moderately complex models as the GTR+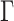 substitution model with
substitution model with 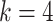 rates categories. The G-NSPR proposal seems more competitive as its efficiency condition is reached when
rates categories. The G-NSPR proposal seems more competitive as its efficiency condition is reached when 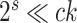 . Even if this condition is not reached, a G-NSPR can be executed at a fraction
. Even if this condition is not reached, a G-NSPR can be executed at a fraction 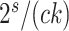 of a partial likelihood evaluation, which represents a reasonable computational overhead for small values of
of a partial likelihood evaluation, which represents a reasonable computational overhead for small values of 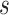 .
.
While the overhead cost of adaptive proposals is nonnegligible compared to naive proposals, their computational overhead remains negligible with respect to partial likelihood evaluations as long as 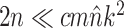 , where
, where 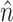 is the number of edges included in a partial likelihood evaluation. This efficiency condition is met even for the simple models (e.g., nucleotide substitutions model without rate heterogeneity,
is the number of edges included in a partial likelihood evaluation. This efficiency condition is met even for the simple models (e.g., nucleotide substitutions model without rate heterogeneity, 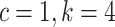 ) as long as
) as long as 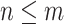 (which is a prerequisite to obtain accurate inferences of phylogeny).
(which is a prerequisite to obtain accurate inferences of phylogeny).
Assessing the Performance of Tree Proposals
Diagnosing the behavior of an MCMC algorithm is generally achieved by monitoring its sampling performance (e.g., effective sample size) on different parameters. This task is particularly difficult when monitoring the performance of MCMC algorithms to estimate the posterior distribution of trees due to the discrete nature of this parameter. Nonetheless, two different characteristics are usually monitored. The first characteristic is the time to convergence of the MCMC algorithm, that is the number of iterations required until the Markov chain reaches its equilibrium. The second characteristic is the mixing efficiency, that is, the propensity of the MCMC algorithm to mimic the process of directly drawing samples from the true posterior distribution.
Few robust and practical procedures exist to measure these two characteristics for samples of phylogenetic trees and none are able to separately monitor the behavior of tree proposals within a mixture. In the next sections, I first enumerate the existing procedures and define how I use them. Then, I present a novel metric able to isolate and assess the performance of tree proposals contained in a mixture of proposals.
Existing performance metrics
The standard metric to assess the convergence of MCMC runs estimating the posterior distribution of trees is the average standard deviation of split frequencies (ASDSF). This metric captures the variance of the posterior distribution of split frequencies among several independent MCMC runs. In previous studies, the efficiency of tree proposals was assessed using a convergence threshold based on the ASDSF (Lakner et al. 2008; Höhna and Drummond 2012). After a thorough investigation of this procedure, Whidden and Matsen (2015) suggested that the number of replicates plays a key role in the accuracy of this metric and proposed an alternative metric. This metric, the mean round trip cover time (MRT), represents the mean number of iterations required to visit each high probability tree, starting from and returning to the highest probability tree. Alas, the MRT could not be applied on diffuse tree distributions and required MCMC runs consisting of an enormous number of samples. Lastly, Lanfear et al. (2016) proposed several metrics to approximate effective sample sizes (ESS) for tree topologies by mapping tree topologies into a continuous parameter and then by applying standard approaches to estimate the ESS. In practice, this is achieved by measuring pairwise distances between tree topologies. While these approximate ESS methods are very promising to diagnose MCMC runs, they are not appropriate for a benchmark of tree proposals. Indeed, using pairwise distances between tree topologies to convert tree topologies into a continuous parameter obfuscates the ability of the proposals to visit each split or tree. This key characteristic of tree proposals is better assessed by the ASDSF and MRT metrics.
I used multiple long and independent runs with MrBayes to obtain accurate estimates of the posterior distribution of split frequencies 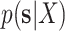 . These reference split frequencies were used to assess the convergence of each one of the runs under two scenarios: the overall convergence of the MCMC run (before burnin removal) and convergence after removal of the burnin phase. The first metric informs on the number of iterations required to reach convergence, while the second indicates the efficiency of the proposals at estimating the split frequencies. I defined these convergence criteria as satisfied when the Euclidean distance between the reference
. These reference split frequencies were used to assess the convergence of each one of the runs under two scenarios: the overall convergence of the MCMC run (before burnin removal) and convergence after removal of the burnin phase. The first metric informs on the number of iterations required to reach convergence, while the second indicates the efficiency of the proposals at estimating the split frequencies. I defined these convergence criteria as satisfied when the Euclidean distance between the reference 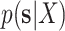 and the estimated
and the estimated 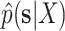 marginal distribution of split frequencies for all splits
marginal distribution of split frequencies for all splits 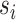 with
with 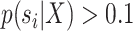 was lower than a fixed threshold. I defined these thresholds to represent an average error of
was lower than a fixed threshold. I defined these thresholds to represent an average error of 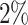 and
and 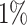 per split for the before and after-burnin removal convergence metrics, respectively.
per split for the before and after-burnin removal convergence metrics, respectively.
Assessing the Contribution of Moves in a Mixture of Proposals
The aforementioned convergence metrics (e.g., ASDSF) capture the behavior of MCMC runs without providing information on the performance of the different tree proposals composing a mixture of proposals. Except for the acceptance rate of each tree proposal, no metrics are readily available to measure the relative contribution of each proposal. The acceptance rate is informative of the proposal behavior, but fails to capture the number of trees that the proposal can access or alter: a proposal could have a high acceptance rate but only visit a small fraction of the 95% credible set. For the same reason, running MCMC analyses using a single tree proposal to measure its convergence performance (e.g., MRT) could prove impossible for some proposals due to their inability to reach some parts of the tree space. Failure to reach convergence is unrepresentative of the mixing efficiency of tree proposals and could lead us to discard proposals that efficiently sample the posterior distribution of trees once convergence is reached.
I therefore considered an alternative approach to characterize the performance of each tree proposal in a mixture of proposals. This strategy starts by defining an idealized tree proposal. This reference proposal is simply the joint posterior distribution of parameters 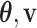 and trees
and trees 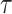 . The expected behavior of this idealized proposal is compared to the measured behavior of practical tree proposals with regard to their ability to visit splits. Focusing on the split-wise behavior of proposals rather than the generated sequences of trees has a significant advantage: the behavior of a proposal with respect to a given split can be summarized by the average number of moves it takes for the proposal to visit, and then revisit this split.
. The expected behavior of this idealized proposal is compared to the measured behavior of practical tree proposals with regard to their ability to visit splits. Focusing on the split-wise behavior of proposals rather than the generated sequences of trees has a significant advantage: the behavior of a proposal with respect to a given split can be summarized by the average number of moves it takes for the proposal to visit, and then revisit this split.
During an MCMC run, the number of moves, or number of iterations, taken by a proposal to visit and then revisit a split identifies a cycle-visit. A cycle-visit starts with the appearance of the split in the tree being sampled. It then includes the number of subsequent iterations when the split is still sampled, plus the number of iterations when the split is not sampled, until its first reappearance. When trees are drawn directly from the posterior distribution, the frequency of a cycle-visit depends entirely on the marginal posterior probability of a split and can be derived by considering the sum of two geometric random variables (Sen and Balakrishnan 1999). These variables are the number of iterations before the disappearance of the split in the trees sampled and the number of iterations before its reappearance, respectively. The probability of a period of length 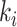 for a full visit-cycle given the split posterior probability
for a full visit-cycle given the split posterior probability 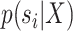 is given as,
is given as,
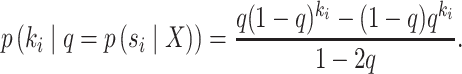 |
(25) |
and is undefined for 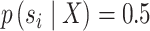 .
.
Assuming that accurate estimates of the split frequencies are available (e.g., reference runs), the characteristics of the ideal tree proposal can then be summarized on a split-wise basis by considering the expected period 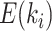 of splits
of splits 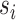 . These expected periods can be estimated numerically using Equation (25). Figure 6a,b shows examples of splits posterior probabilities
. These expected periods can be estimated numerically using Equation (25). Figure 6a,b shows examples of splits posterior probabilities 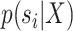 and expected cycle-visit frequencies (i.e.,
and expected cycle-visit frequencies (i.e., 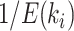 ) for the reference ideal proposal. In practice, that is during an MCMC run, the expected cycle-visit (C-V) frequencies for each proposal can be estimated under the condition that the full proposal history is tracked by logging the iteration at which they are applied and the resulting effect on the splits existing in the sampled tree. Figure 6c–e shows examples of these estimates (i.e.,
) for the reference ideal proposal. In practice, that is during an MCMC run, the expected cycle-visit (C-V) frequencies for each proposal can be estimated under the condition that the full proposal history is tracked by logging the iteration at which they are applied and the resulting effect on the splits existing in the sampled tree. Figure 6c–e shows examples of these estimates (i.e., 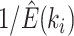 ) for three proposals used in a single MCMC run (i.e., stNNI, eSPR and A-stNNI proposals).
) for three proposals used in a single MCMC run (i.e., stNNI, eSPR and A-stNNI proposals).
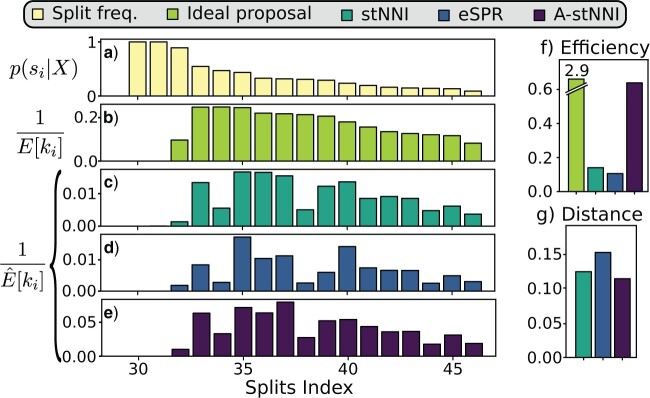
Figure 6.
Example of the cycle-visit metrics for a single analysis. Panel a) displays the reference split frequencies. b) The C-V frequencies for an idealized proposal. c)–e) The observed C-V frequencies for the stNNI, eSPR, and A-stNNI proposals, respectively. These frequencies differs in amplitude across proposals (e.g., split 34) and from the ideal behavior shown in b). f) and g) The summarized statistics for each proposal, that is the resulting C-V efficiency and C-V distance metrics.
In this study, I use the expected C-V frequencies to define two metrics characterizing the performance of a tree proposal. The first metric consists in summing the C-V frequencies estimated for a given proposal for all splits having an estimated posterior probability 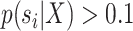 . This metric, the C-V efficiency, captures how many new splits are visited on average per proposed moves. This value integrates implicitly the acceptance rate of the proposal and the number of splits altered by the moves, but does not indicate if the splits coverage of the proposal is adequate. Indeed, a proposal could be characterized by a good C-V efficiency while being unable to visit several splits. Figure 6f provides an example of the C-V efficiency of the ideal proposal as well as the ones used during the MCMC run. In this example, the C-V efficiency indicates that the A-stNNI proposal outperformed the naive proposals while performing significantly worse than the ideal proposal. For proposals modifying a unique split per move, the C-V efficiency is directly linked to the acceptance rate of the proposals (e.g., 0.12 and 0.61 for the stNNI and A-stNNI, respectively).
. This metric, the C-V efficiency, captures how many new splits are visited on average per proposed moves. This value integrates implicitly the acceptance rate of the proposal and the number of splits altered by the moves, but does not indicate if the splits coverage of the proposal is adequate. Indeed, a proposal could be characterized by a good C-V efficiency while being unable to visit several splits. Figure 6f provides an example of the C-V efficiency of the ideal proposal as well as the ones used during the MCMC run. In this example, the C-V efficiency indicates that the A-stNNI proposal outperformed the naive proposals while performing significantly worse than the ideal proposal. For proposals modifying a unique split per move, the C-V efficiency is directly linked to the acceptance rate of the proposals (e.g., 0.12 and 0.61 for the stNNI and A-stNNI, respectively).
The second metric, the C-V distance, is complementary to the first one and represents the splits coverage of the proposals by comparing the expected C-V frequencies per split of the idealized proposal to the ones estimated for the proposal of interest. In other words, this metric, the C-V distance, represents the departure from the relative expected C-V frequencies of the ideal proposal and is therefore defined as the Euclidean distance between the normalized C-V frequencies of the ideal proposal and the one of interest,
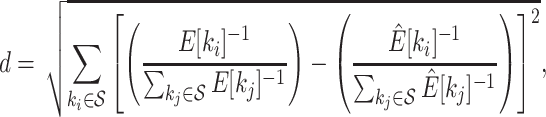 |
(26) |
where 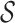 identifies all cycle-periods
identifies all cycle-periods 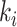 of splits
of splits 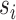 having a posterior frequency
having a posterior frequency 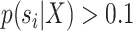 . The C-V frequencies are rescaled to remove the effect of the C-V efficiency, or amplitude of the C-V frequencies. An example of C-V distances is shown in Figure 6g. In this example, the eSPR proposal has a larger C-V distance than the two others because it struggles to visit splits 34 and 38 (Fig. 6c–e). In conclusion, the C-V efficiency and distance shown in Figure 6f,g highlight that the A-stNNI proposal is at least three times more efficient according to the C-V efficiency and covers splits as well as the stNNI proposal.
. The C-V frequencies are rescaled to remove the effect of the C-V efficiency, or amplitude of the C-V frequencies. An example of C-V distances is shown in Figure 6g. In this example, the eSPR proposal has a larger C-V distance than the two others because it struggles to visit splits 34 and 38 (Fig. 6c–e). In conclusion, the C-V efficiency and distance shown in Figure 6f,g highlight that the A-stNNI proposal is at least three times more efficient according to the C-V efficiency and covers splits as well as the stNNI proposal.
To simplify the interpretation of the C-V distance in upcoming benchmarks, I will consider the inverse of this metric (i.e., 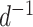 ): the C-V coverage. This transformed metric conveniently increases as the proposal behavior approaches the one of the ideal proposal.
): the C-V coverage. This transformed metric conveniently increases as the proposal behavior approaches the one of the ideal proposal.
Results
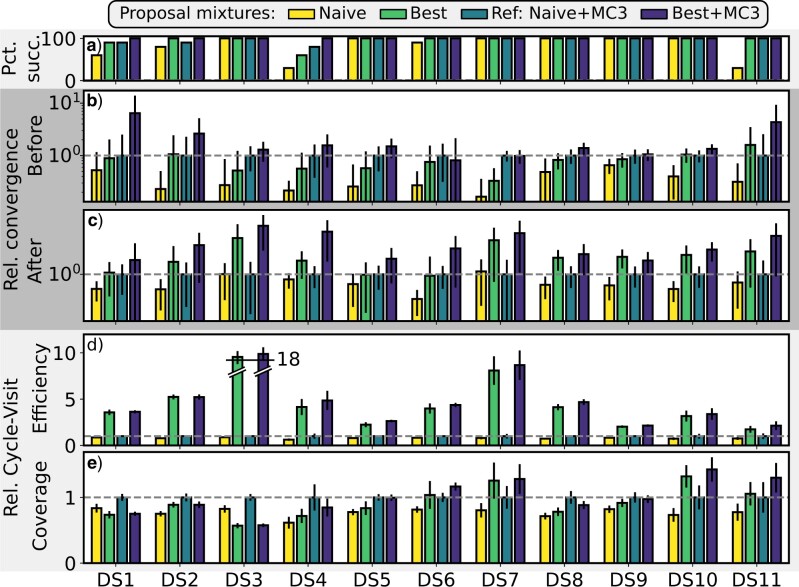
This study is decomposed in two separate experiments. First, I assessed the performance of each proposal separately and validated the new efficiency metrics on data sets (i.e., SIM1 to SIM4) simulated with the INDElible software (Fletcher and Yang 2009). Trees were simulated under a birth–death model and alignments were simulated under the GTR model (Supplementary material available on Dryad, data set simulation settings). Then, I assessed the performance of a proposal mixture containing adaptive proposals by comparing it to the traditional mixture of naive proposals. This comparison was conducted using 11 empirical data sets (i.e., DS1 to DS11) commonly used to evaluate tree proposals (Table S2 of the Supplementary material available on Dryad; Lakner et al. 2008; Höhna and Drummond 2012; Whidden and Matsen 2015).
Set-up of the Analyses
I analyzed each data set with MrBayes (Ronquist et al. 2012) to obtain accurate estimates of the tree and split posterior distributions. Simulated and empirical data sets were analyzed under the GTR model and GTR+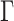 model with four categories, respectively (Supplementary material available on Dryad, Priors settings). Analyses of at least 50 million iterations with four Metropolis-coupled chains were replicated three times and used to define the reference split frequencies. Each analysis reached an ASDSF value smaller than
model with four categories, respectively (Supplementary material available on Dryad, Priors settings). Analyses of at least 50 million iterations with four Metropolis-coupled chains were replicated three times and used to define the reference split frequencies. Each analysis reached an ASDSF value smaller than 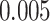 , suggesting that runs converged properly.
, suggesting that runs converged properly.
The adaptive and parsimony-guided proposals are implemented in the CoevRJ software (Meyer et al. 2019), which is designed to simultaneously infer phylogenies and molecular coevolution. This software also includes more traditional models such as the GTR+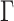 model. I therefore used the GTR+
model. I therefore used the GTR+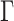 model to assess proposal performance and conducted analyses of 10 million iterations with 10 independent chains for each proposal mixture and data set with the same models and prior settings used to build the reference split frequencies. I then conducted additional runs with three Metropolis-coupled chains for the empirical data sets (using the same settings, iterations, and number of replicates as their MCMC equivalent).
model to assess proposal performance and conducted analyses of 10 million iterations with 10 independent chains for each proposal mixture and data set with the same models and prior settings used to build the reference split frequencies. I then conducted additional runs with three Metropolis-coupled chains for the empirical data sets (using the same settings, iterations, and number of replicates as their MCMC equivalent).
Mixtures of Proposals
Five different proposal mixtures were considered for these experiments (Table S1 of the Supplementary material available on Dryad). The reference mixture is the naive mixture composed of the stNNI, eSPR and eTBR proposals applied each at equal frequency (as in MrBayes), with a probability 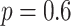 of extending a path for eSPR and eTBR. This probability was chosen based on empirical observations and according to Lakner et al. (2008). All subsequent mixtures applied stNNI and eSPR proposals at low frequency as a baseline.
of extending a path for eSPR and eTBR. This probability was chosen based on empirical observations and according to Lakner et al. (2008). All subsequent mixtures applied stNNI and eSPR proposals at low frequency as a baseline.
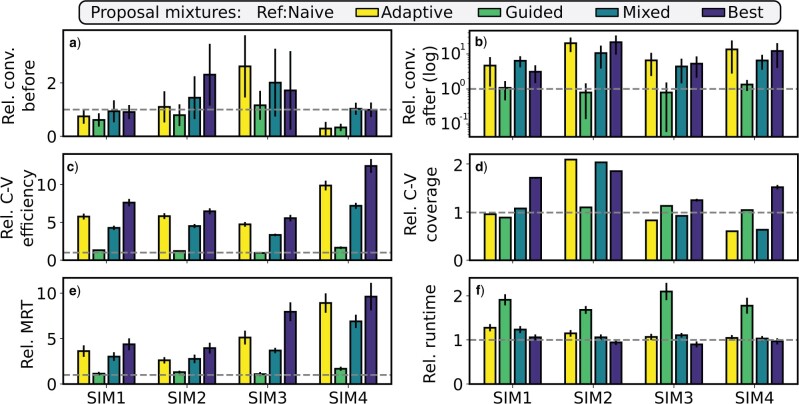
The adaptive and guided mixtures were composed of all adaptive (i.e., A-stNNI, A-2SPR, and A-PBJ) and guided (i.e., G-stNNI, G-1SPR, G-2SPR) proposals, respectively, each applied at equal frequencies. The mixed mixture applied all the adaptive and guided proposals with equal frequencies, with the exception of the G-stNNI that was removed due to its expensive computational cost. Finally, the best mixture was a version of the mixed mixture where the proposal weights were tuned for performance based on empirical observations.
Representation of the Performance Metrics
Each of the experiments presented in the following sections describes the performance of several proposals or proposal mixtures across many data sets. To homogenize the performance metrics measured across data sets, relative metrics are reported using a representative proposal or mixture involved in the experiment as reference. For instance, when individual proposals or mixtures of proposals are compared, the stNNI proposal or naive mixture are respectively chosen as reference. Reporting the C-V efficiency for the A-stNNI proposal is then achieved by presenting the ratio of the C-V efficiency measured for the A-stNNI proposal and the C-V efficiency of the reference proposal (e.g., stNNI). This metric representation highlights the magnitude of the performance improvements regardless of the data set.
Similarly, different proposals or mixtures may have significantly different computational costs. Therefore, the relative C-V efficiency and convergence metrics reported in the experiments are weighted by the relative computational time unless specified otherwise. In other words, the performance gains reported for a metric (e.g., increase in C-V efficiency) include differences in computational costs (e.g., slower proposal) to identify the effective performance gains. However, this transformation is not applied to the relative C-V coverage metric given that the time-component is already accounted for in the relative C-V efficiency. The relative C-V coverage remains then a straight comparison of the split-coverage of two proposals or mixtures.
Lastly, while these transformed metrics allow us to quickly compare the effective performance increases or decreases in a given experiment, they also obfuscate the raw measurements. Therefore, raw metrics (i.e., absolute value) are reported in the Supplementary material available on Dryad (Figs. S11 to S17 of the Supplementary material available on Dryad).
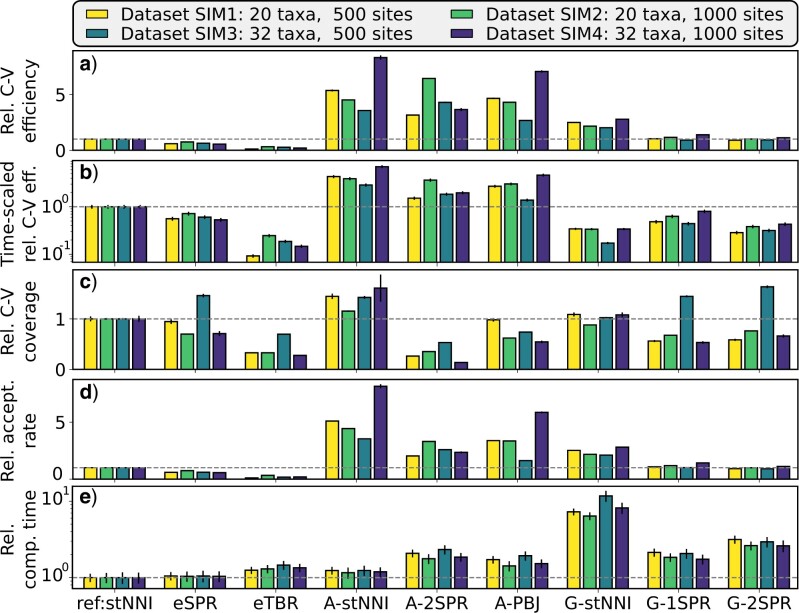
Performance of Proposal Mixtures on Simulated Data Sets
Proposal Performance
On the four simulated data sets, the adaptive proposals achieved the best mixing efficiency according to the C-V efficiency with consistent 2- to 8-fold performance improvements over the stNNI proposal (Fig. 7a). These increases in mixing efficiency for the A-stNNI proposal were not affected by its inherent increase in computational cost (Fig. 7b). Despite slight decreases in C-V efficiency gains after being rescaled from the relative computational time, the more complex adaptive proposals (i.e., A-2SPR and A-PBJ) consistently demonstrated significant performance gains in comparison to all the naive and parsimony-guided proposals. These increases in C-V efficiency were mirrored by increased acceptance rates (Fig. 7d). As shown by the relative C-V coverage (Fig. 7c), most proposals modifying several edges (e.g., eTBR, A-2SPR, or G-2SPR) were less prone to visit all splits according to the theoretical expectation than the one-edge proposals (e.g., stNNI, A-stNNI, or G-stNNI). In general, the relative C-V efficiency and coverage highlight that the proposals were either strictly better than the stNNI (i.e., A-stNNI), more efficient regarding specific splits (i.e., A-2SPR and A-PBJ) or worse (i.e., the remaining proposals, except on data set 3). Lastly, the measured computational cost for each proposal reflected the theoretical complexity, and particularly affected the G-stNNI proposal with a nearly 10-fold increase in computational cost (Fig. 7d).
Figure 7.
Relative performance improvements of proposals on four simulated data sets using the stNNI proposal as reference. a) and b) The relative C-V efficiency for each proposal without and with penalization for their computational costs, respectively. c) and d) The relative increase in C-V coverage and acceptance rate, respectively. e) The relative computational time for the whole MCMC iteration (proposal and likelihood computational time). Absolute values are available in Figures S11–S15 of the Supplementary material available on Dryad.
The performance of the naive proposals worsened proportionally to the number of splits modified by a move, as shown by the decreases in all metrics (Fig. 7). Regardless of the proposal’s performance, using moves that alter multiple splits remains a mandatory feature for the estimation of tree distributions to ensure the proper exploration of the tree space. For instance, eSPR-type moves were able to visit tree topologies containing splits hardly reachable by stNNI-type proposals on data set SIM3; this advantageous feature was captured by the C-V coverage (Fig. 7c for data set SIM3). The parsimony-guided proposals, as implemented in this study, performed poorly in term of mixing efficiency. The G-stNNI proposal was the only parsimony-guided proposal to improve the C-V efficiency by up to 2.5-fold factor, but at the cost of a 10-fold increase in computational cost. In practice, the G-stNNI remained therefore less efficient than the naive and adaptive stNNI (Fig. 7b).
The A-stNNI proposal appeared to be the best overall proposal by achieving consistent increases in C-V efficiency and C-V coverage without leading to significant increases in computational cost. The adaptive N-edges proposals, the A-2SPR and A-PBJ presented different but complementary behaviors. The A-2SPR was very efficient at visiting a subset of the splits, while the A-PBJ acted as a slightly less efficient N-edges version of the A-stNNI. These two adaptive proposals outperformed all their N-edges counterparts and therefore represent the best alternatives to the eSPR and eTBR proposals.
Mixture Performance and Metric Behaviors
The mixed and best proposal mixtures converged toward the reference split frequencies as fast, if not faster, than the naive mixture (Fig. 8a). These mixtures, containing all types of proposals, were more consistent with respect to MCMC convergence than the mixtures composed of a single proposal type (e.g., adaptive). After removing the burnin, mixtures containing adaptive proposals accurately estimated the split frequencies 3–12 times faster than the naive and guided mixtures (Fig. 8b). According to the C-V efficiency and the MRT metrics, the adaptive and best mixtures were up to 12 times more efficient at sampling the posterior distribution of trees (Fig. 8c,e). Their performance was closely followed by the mixed mixture but remained unequaled by the guided mixture. The C-V coverage metric indicated that the guided mixture behaved similarly to the reference and that the best mixture was the only one to consistently perform as well or better than the naive mixture (Fig. 8d). In summary, the adaptive, mixed and best mixtures more frequently visited splits than the other mixtures but only the best mixture was able to consistently improve the split coverage (i.e., C-V coverage).
Figure 8.
Relative performance gains of proposal mixtures on four simulated data sets (i.e., SIM1 to SIM4) using the naive mixture as reference. a) and b) The acceleration in convergence time before and after removal of the burnin phase, respectively. Convergence thresholds were fixed to a 2% and 1% average error per split. c–f) Increases in C-V efficiency, C-V coverage, MRT, and overall runtime, respectively. a), b), c) and e) are weighted by the relative runtime of f). Absolute values are available in Figure S16 of the Supplementary material available on Dryad.
Most of the mixtures of proposals took slightly more computational time to reach 10 million iterations than the reference mixture. The best mixture was the only one to have a similar computational cost (Fig. 8f). The decreases in runtime observed on data set SIM2 and SIM3 were due to a significant increase in the acceptance rate of the adaptive proposals. The rejection of a proposal by the MCMC process induces computational procedures that restore the previous MCMC state. These procedures involve costly operations (i.e., memory backups or re-evaluations of likelihoods) that are avoided whenever a move is accepted. Lastly, the only mixture that significantly underperformed in terms of runtime was the guided mixture due to the computational expense of the G-stNNI proposal.
In addition to assessing the performance of the different proposal mixtures on simulated data sets, this experiment indicated that the C-V and MRT metric were significantly more stable than the convergence metrics. Convergence metrics are more likely to be impacted by the starting tree topology and stochastic behavior of the MCMC algorithm. More importantly, this experiment highlighted that the C-V efficiency and the MRT metrics were consistently measuring improvements within the same order of magnitude for all data sets and proposals.
Proposal Mixture Performance on Empirical Data Sets
The best proposal mixture consistently outperformed the naive mixture, regardless of whether MC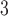 was used (Fig. 9c,d). On challenging data sets, the use of the best mixture without MC
was used (Fig. 9c,d). On challenging data sets, the use of the best mixture without MC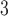 increased the amount of successful MCMC runs but did not guarantee convergence within the imposed 10 million iterations (Fig. 9a). The best mixture with MC
increased the amount of successful MCMC runs but did not guarantee convergence within the imposed 10 million iterations (Fig. 9a). The best mixture with MC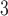 was the only setting under which convergence was consistently achieved. Overall, the best mixture without MC
was the only setting under which convergence was consistently achieved. Overall, the best mixture without MC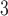 led to runs converging as fast as the naive mixture with MC
led to runs converging as fast as the naive mixture with MC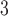 and surpassed its performance when MC
and surpassed its performance when MC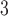 was not used (Fig. 9b). These improvements came at no significant additional computational cost: the variation in computational costs reached at most 11% of the reference cost, depending on the data sets and mixtures (Figs. S17f and S18 of the Supplementary material available on Dryad).
was not used (Fig. 9b). These improvements came at no significant additional computational cost: the variation in computational costs reached at most 11% of the reference cost, depending on the data sets and mixtures (Figs. S17f and S18 of the Supplementary material available on Dryad).
Figure 9.
Relative performance gains on empirical data sets using the naive mixture with MC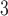 as reference. a) The percentage of runs having succeeded to converge within 10 million iterations. b) and c) The acceleration in convergence time before and after removal of the burnin phase, respectively. Convergence thresholds were fixed to a 2% and 1% average error per split. Panels d) and e) report increases in C-V efficiency and coverage. b), c) and d) are weighted by the relative runtime shown in Figure S18 of the Supplementary material available on Dryad. Absolute values are available in Figure S17 of the Supplementary material available on Dryad.
as reference. a) The percentage of runs having succeeded to converge within 10 million iterations. b) and c) The acceleration in convergence time before and after removal of the burnin phase, respectively. Convergence thresholds were fixed to a 2% and 1% average error per split. Panels d) and e) report increases in C-V efficiency and coverage. b), c) and d) are weighted by the relative runtime shown in Figure S18 of the Supplementary material available on Dryad. Absolute values are available in Figure S17 of the Supplementary material available on Dryad.
Using the best mixture led on average to a 6-fold increase in C-V efficiency (with and without MC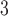 ) when compared to the reference mixture (naive plus MC
) when compared to the reference mixture (naive plus MC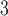 ). The magnitude of the observed improvements were different depending on the data sets analyzed: the performance of the best mixture was directly correlated with the amount of information exploitable by the adaptive proposals in the distribution of split frequencies (Text and Fig. S10 of the Supplementary material available on Dryad).
). The magnitude of the observed improvements were different depending on the data sets analyzed: the performance of the best mixture was directly correlated with the amount of information exploitable by the adaptive proposals in the distribution of split frequencies (Text and Fig. S10 of the Supplementary material available on Dryad).
Analyses on data sets with diffuse posterior tree distributions (i.e., DS5, DS9, and DS11) had only limited improvements in C-V efficiency that ranged from 2- to 2.7-fold. Removing duplicated sequences from alignments DS9 and DS11 significantly increased their relative performance (from 2.2- to 3.2- and 2- to 5.9-fold increases, respectively; Fig. S10 of the Supplementary material available on Dryad). For data sets with strong phylogenetic signal (e.g., DS3), the relative performance reached up to an 18-fold efficiency increase. These observations could not be confirmed with the MRT metric due to the difficulty of applying it to diffuse tree topology distributions (Whidden and Matsen 2015). However, the observed trends of improvements and their magnitude concurred with the improvements in convergence speed after burnin removal (Fig. 9c).
Using the MC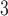 algorithm had a positive effect on the convergence of Markov chains regardless of the proposal mixture: all the runs converged with the best mixture and only a few failed with the naive mixture. These convergence failures happened on the three data sets (i.e., DS1, DS2, DS4) with the highest C-V distances (Fig. S17 of the Supplementary material available on Dryad), indicating that many of their splits were difficult to visit. Nonetheless, when MC
algorithm had a positive effect on the convergence of Markov chains regardless of the proposal mixture: all the runs converged with the best mixture and only a few failed with the naive mixture. These convergence failures happened on the three data sets (i.e., DS1, DS2, DS4) with the highest C-V distances (Fig. S17 of the Supplementary material available on Dryad), indicating that many of their splits were difficult to visit. Nonetheless, when MC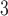 was used, convergence was reached on average 4.2 and 2 times faster before and after burnin removal, respectively. These improvements regarding the convergence were not mirrored by the C-V efficiency metric, indicating that the sampling efficiency of the cold chain remained mostly unaffected by MC
was used, convergence was reached on average 4.2 and 2 times faster before and after burnin removal, respectively. These improvements regarding the convergence were not mirrored by the C-V efficiency metric, indicating that the sampling efficiency of the cold chain remained mostly unaffected by MC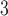 . The convergence improvements and small but systematic improvements in C-V coverage resulting from the use of MC
. The convergence improvements and small but systematic improvements in C-V coverage resulting from the use of MC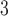 were, however, consistent with the effect of accepting bolder moves that could enable the exploration of different peaks of the posterior distribution (Fig. 9e).
were, however, consistent with the effect of accepting bolder moves that could enable the exploration of different peaks of the posterior distribution (Fig. 9e).
In several instances, the best mixture slightly increased the C-V coverage. The few instances in which the C-V coverage decreased despite increased C-V efficiency and faster convergences falls into two categories. First, this phenomenon occurred on data sets having splits that were difficult to access (i.e., DS1, DS2, DS4). Second, it occurred in instances (i.e., DS2 and DS8) where the A-2SPR proposal was only able to reach a subset of splits due to the rigid nature of its moves (i.e., 2-edges), but with high efficiency (i.e., with approximately 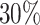 acceptance rate). In both cases, the best mixture and more precisely the adaptive tree proposals were only able to improve the visit frequency of a subset of splits. The resulting discrepancy in visit frequencies across all splits led therefore to an increase in C-V distance. These observations suggest that the dominant effect of the adaptive proposals was to increase the overall frequency at which appropriate moves were proposed, rather than to specifically allow to visit splits unreachable by naive proposals (e.g., multiple peaks).
acceptance rate). In both cases, the best mixture and more precisely the adaptive tree proposals were only able to improve the visit frequency of a subset of splits. The resulting discrepancy in visit frequencies across all splits led therefore to an increase in C-V distance. These observations suggest that the dominant effect of the adaptive proposals was to increase the overall frequency at which appropriate moves were proposed, rather than to specifically allow to visit splits unreachable by naive proposals (e.g., multiple peaks).
In summary, using the best mixture consistently improved the sampling of the posterior distribution. In practice, it improved the odds of reaching convergence on challenging data sets with and without MC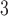 (e.g., DS1 or DS4, Fig. 9a) and had a significant impact on the computational time required to obtain accurate estimates of split frequencies (Tables S3, S4 and Fig. S19 of the Supplementary material available on Dryad). The computational time required to obtain accurate split frequencies (i.e., convergence at 1% error per split after burnin removal, Fig. 9c) reduced from 3 h on average with the naive mixture to 25 minutes with the best mixture with MC
(e.g., DS1 or DS4, Fig. 9a) and had a significant impact on the computational time required to obtain accurate estimates of split frequencies (Tables S3, S4 and Fig. S19 of the Supplementary material available on Dryad). The computational time required to obtain accurate split frequencies (i.e., convergence at 1% error per split after burnin removal, Fig. 9c) reduced from 3 h on average with the naive mixture to 25 minutes with the best mixture with MC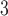 on DS11. Similar reductions in computational time were measured under the same settings, for instance, on DS2 (3 h 20 min to 45 min) or DS4 (5 h 30 min to 40 min). Even for less challenging analyses where MC
on DS11. Similar reductions in computational time were measured under the same settings, for instance, on DS2 (3 h 20 min to 45 min) or DS4 (5 h 30 min to 40 min). Even for less challenging analyses where MC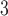 was not required to reach convergence, using the best mixture instead of the naive yielded analogous improvements on the computational time with for instance a reduction from 20 min to 4 min on DS7 or from 1 h to 10 min on DS10.
was not required to reach convergence, using the best mixture instead of the naive yielded analogous improvements on the computational time with for instance a reduction from 20 min to 4 min on DS7 or from 1 h to 10 min on DS10.
Discussion
In this study, I have presented the concept of adaptive proposals for unrooted tree topologies and developed a family of adaptive tree proposals. These adaptive tree proposals generate moves that more efficiently sample the posterior distribution of trees by exploiting an estimate of the marginal split frequencies. This concept was applied to two standard proposals (i.e., stNNI and eSPR) generating specific type of moves. Additionally, I presented a novel approach for the design of tree proposals enabled by the concept of adaptive proposals. This approach was used to design a proposal favoring the most appropriate type of moves out of several (e.g., NNI, SPR, or TBR) by identifying strongly and weakly supported region of the phylogeny using path-building mechanisms. I showed that, while being more computationally expensive than standard proposals, the theoretic computational complexity of adaptive proposals was significantly lower than the complexity of parsimony-guided proposals and likelihood evaluations regardless of the tree size, alignment length and the substitution models used.
The performance of these adaptive tree proposals was assessed on simulated and empirical data sets using the CoevRJ software. Using performance metrics designed for these experiments, I showed that adaptive proposals consistently outperformed their counterparts on simulated data sets. Using an empirically tuned proposal mixture to analyze 11 empirical data sets resulted in 2- to 18-fold improvements in mixing efficiency and up to 6 times faster convergence of MCMC and MC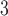 runs when compared to a standard proposal mixture composed of stNNI, eSPR, and eTBR proposals. In practice, these performance improvements were correlated with the amount of phylogenetic signal in the alignments, and resulted in significant reductions of the computational time required to accurately estimate the split frequencies (e.g., from 3 h with naive proposals to 25 min with adaptive proposals).
runs when compared to a standard proposal mixture composed of stNNI, eSPR, and eTBR proposals. In practice, these performance improvements were correlated with the amount of phylogenetic signal in the alignments, and resulted in significant reductions of the computational time required to accurately estimate the split frequencies (e.g., from 3 h with naive proposals to 25 min with adaptive proposals).
Adaptive proposals proved to be superior to naive and parsimony-guided proposals according to all metrics of performance. The first key advantage of adaptive proposals is their ability to locate regions of a tree topology subject to uncertainties that could benefit from being modified. Nonadaptive proposals always start by arbitrarily choosing a region of the tree topology to modify. After this first arbitrary choice, naive proposals continue to apply randomized topological modification, while guided proposals use a score (e.g., parsimony or posterior probability; Höhna and Drummond 2012) to select the most promising resulting tree from a finite set of trees. Even if the guiding mechanism leads to good alterations, these proposals remain limited by the arbitrary initial choice. I investigated an alternative approach for parsimony-guided proposals that involved an exhaustive exploration of all possible stNNI moves for a given tree. This proposal’s mixing efficiency was better than naive proposals but worse than adaptive proposals. Furthermore, its computational complexity exceeded the cost of a likelihood evaluation by an order of magnitude, and made the proposal generally impractical.
The second key advantage of adaptive proposals is their ability to exploit the shape of the posterior distribution of trees by cheaply approximating the split frequencies during an MCMC run. Contrary to guided proposals using proxy scores to approximate the posterior distribution (e.g., parsimony), the performance of adaptive proposals does not depend on the accuracy or the computational efficiency of the proxy score. However, this second key advantage is also a potential pitfall because the adaptive proposals strongly rely on adequate estimates of the split frequencies. Very inaccurate estimates could lead adaptive proposals to have worse performance than their naive counterparts. This outcome was not observed on the 11 empirical data sets analyzed in this study, despite the ruggedness of their posterior distribution of trees (Whidden and Matsen 2015).
The concept of adaptive proposals is not limited to the three adaptive proposals developed in this study, but opens new avenues toward the development of other tree proposals. For instance, the design approach used for the A-PBJ proposal that involves proposals adaptively defining the move type (e.g., subtree swap or pruning-and-regrafting) using the marginal split frequencies, could lead to other novel proposals by considering other path-building or structure-building strategies. Another avenue for improvements would be to estimate the joint distribution of split frequencies and exploit this information to consider bolder and more complex topological alterations. While the use of adaptive proposals could clearly benefit other types of phylogenetic inferences, these additional developments would be particularly beneficial to models having stronger constraints, such as clock-constrained trees or the inference of gene-trees within species trees (Rannala and Yang 2017).
In conclusion, the three adaptive tree topology proposals defined in this study represent a practical improvement to the existing tree proposals, regardless of the substitution model considered. The concepts developed offer a fresh perspective on the design of tree proposals that should be advantageous to more challenging types of phylogenetic inferences and could therefore bring a new outlook to a challenging limitation existing since the early days of Bayesian inference of phylogenies.
Data and Software Availability
The CoevRJ software and the empirical data used in this manuscript can be found in the CoevRJ repository: https://bitbucket.org/XavMeyer/coevrj.
Acknowledgments
I thank M. R. May for his valuable feedback on this project and manuscript, and J. H. Huelsenbeck for enlightening discussions on the subject. Finally, I am grateful for the insightful reviews from J. M. Brown and two anonymous referees that greatly improved the manuscript.
Supplementary Material
Data available from the Dryad Digital Repository: https://dx.doi.org/10.6078/D16D9P.
Funding
This work was supported by the Swiss National Science Foundation (P2GEP2_178032 and P400PB_186777).
References
- Aberer A.J., Kobert K., Stamatakis A. (2014). Exabayes: massively parallel Bayesian tree inference for the whole-genome era. Mol. Biol. Evol. 31(10):2553–2556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aberer A.J., Stamatakis A., Ronquist F. (2015). An efficient independence sampler for updating branches in Bayesian Markov chain Monte Carlo sampling of phylogenetic trees. Syst. Biol. 65(1):161–176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Altekar G., Dwarkadas S., Huelsenbeck J.P., Ronquist F. (2004). Parallel Metropolis coupled Markov chain Monte Carlo for Bayesian phylogenetic inference. Bioinformatics 20(3):407–415. [DOI] [PubMed] [Google Scholar]
- Andrieu C., Thoms J. (2008). A tutorial on adaptive MCMC. Stat. Comput. 18(4):343–373. [Google Scholar]
- Baele G., Lemey P., Rambaut A., Suchard M.A. 2017. Adaptive MCMC in Bayesian phylogenetics: an application to analyzing partitioned data in BEAST. Bioinformatics 33(12):1798–1805. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beiko R.G., Keith J.M., Harlow T.J., Ragan M.A. (2006). Searching for convergence in phylogenetic Markov chain Monte Carlo. Syst. Biol. 55(4):553–565. [DOI] [PubMed] [Google Scholar]
- Brown J.M., Thomson R.C. (2018). The behavior of Metropolis-coupled Markov chains when sampling rugged phylogenetic distributions. Syst. Biol. 67(4):729–734. [DOI] [PubMed] [Google Scholar]
- Claywell B.C., Dinh V., Fourment M., McCoy C.O., Matsen IV F.A. (2018). A surrogate function for one-dimensional phylogenetic likelihoods. Mol. Biol. Evol. 35(1):242–246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fletcher W., Yang Z. (2009). INDELible: a flexible simulator of biological sequence evolution. Mol. Biol. Evol. 26(8):1879–1888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gelman A., Roberts G.O., Gilks W.R. (1996). Efficient metropolis jumping rules. Bayesian Stat., 5(599-608):42. [Google Scholar]
- Haario H., Saksman E., Tamminen J. (1999). Adaptive proposal distribution for random walk metropolis algorithm. Comput. Stat. 14(3):375–396. [Google Scholar]
- Haario H., Saksman E., Tamminen J. (2001). An adaptive Metropolis algorithm. Bernoulli 7(2):223–242. [Google Scholar]
- Haario, H., Saksman, E., and Tamminen, J. (2005). Componentwise adaptation for high dimensional MCMC. Comput. Stat. 20(2):265–273. [Google Scholar]
- Höhna S., Drummond A.J. (2012). Guided tree topology proposals for Bayesian phylogenetic inference. Syst. Biol. 61(1):1–11. [DOI] [PubMed] [Google Scholar]
- Höhna S., Landis M.J., Heath T.A., Boussau B., Lartillot N., Moore, B.R., Huelsenbeck J.P., Ronquist F. (2016). RevBayes: Bayesian phylogenetic inference using graphical models and an interactive model-specification language. Syst. Biol. 65(4):726–736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huelsenbeck J.P., Ane C., Larget B., Ronquist F. (2008). A Bayesian perspective on a non-parsimonious parsimony model. Syst. Biol. 57(3):406–419. [DOI] [PubMed] [Google Scholar]
- Huelsenbeck J.P., Ronquist F., Nielsen R., Bollback J.P. (2001). Bayesian inference of phylogeny and its impact on evolutionary biology. Science 294(5550):2310–2314. [DOI] [PubMed] [Google Scholar]
- Lakner C., van der Mark P., Huelsenbeck J.P., Larget B., Ronquist F. (2008). Efficiency of Markov chain Monte Carlo tree proposals in Bayesian phylogenetics. Syst. Biol. 57(1):86–103. [DOI] [PubMed] [Google Scholar]
- Lanfear R., Hua X., Warren D.L. (2016). Estimating the effective sample size of tree topologies from Bayesian phylogenetic analyses. Genome Biol. Evol. 8(8):2319–2332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meyer X., Chopard B., Salamin N. (2017). Accelerating Bayesian inference for evolutionary biology models. Bioinformatics 33(5):669–676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meyer X., Dib L., Silvestro D., Salamin N. (2019). Simultaneous Bayesian inference of phylogeny and molecular coevolution. Proc. Natl. Acad. Sci. USA 201813836. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rannala B., Yang Z. (2017). Efficient Bayesian species tree inference under the multispecies coalescent. Syst. Biol. 66(5):823–842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roberts G.O., Rosenthal J.S. (2009). Examples of adaptive MCMC. J. Comput. Graph. Stat. 18(2):349–367. [Google Scholar]
- Ronquist F., Teslenko M., van der Mark P., Ayres D.L., Darling A., Höhna S., Larget B., Liu L., Suchard M.A., Huelsenbeck J.P. (2012). MrBayes 3.2: efficient Bayesian phylogenetic inference and model choice across a large model space. Syst. Biol. 61(3):539–542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sen A., Balakrishnan N. (1999). Convolution of geometrics and a reliability problem. Stat. Probab. Lett. 43(4):421–426. [Google Scholar]
- Swofford D.L., Olsen G.J., Waddell P.J. (1996). Phylogenetic inference. In: “ Hillis D.M., Moritz C., Mable B.K., editors. Molecular systematics, vol. 14. Sunderland, MA: Sinauer. p. 407. [Google Scholar]
- Thawornwattana Y., Dalquen D., Yang Z. (2017). Designing simple and efficient Markov chain Monte Carlo proposal kernels. Bayesian Anal. 13(4):1037–1063. [Google Scholar]
- Whidden C., Matsen F.A. (2015). Quantifying MCMC exploration of phylogenetic tree space. Syst. Biol. 64(3):472–491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Z. (1994). Maximum likelihood phylogenetic estimation from DNA sequences with variable rates over sites: approximate methods. J. Mol. Evol. 39(3):306–314. [DOI] [PubMed] [Google Scholar]
- Yang Z., Rannala B. (1997). Bayesian phylogenetic inference using dna sequences: a Markov chain Monte Carlo method. Mol. Biol. Evol. 14(7):717–724. [DOI] [PubMed] [Google Scholar]
- Yang Z., Rannala B. (2012). Molecular phylogenetics: principles and practice. Nat. Rev. Genet. 13(5):303. [DOI] [PubMed] [Google Scholar]
- Zhang C., Huelsenbeck J.P., Ronquist F. (2020). Using parsimony-guided tree proposals to accelerate convergence in Bayesian phylogenetic inference. Syst. Biol. 69(5):1016–1032. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The CoevRJ software and the empirical data used in this manuscript can be found in the CoevRJ repository: https://bitbucket.org/XavMeyer/coevrj.