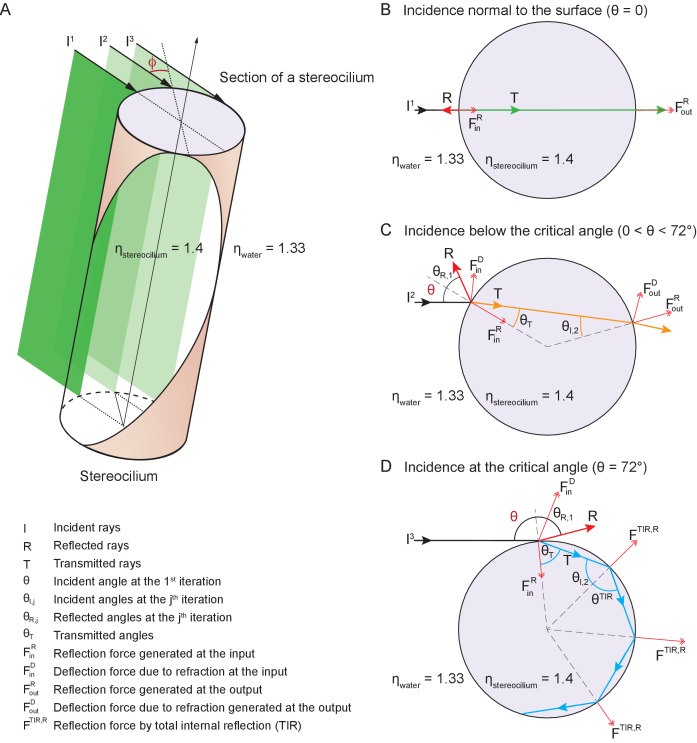
Figure 7. Potential fates of a plane wave incident on a stereocilium.
(A) Three representative rays of a light beam interact with a stereocilium; , and denote the incident, reflected, and transmitted portions of each ray. All superscripts and subscripts are defined in the figure. The rays , , (black arrows) indicate the direction of light in water (refractive index 1.33) as it strikes a stereocilium whose refractive index is 1.4 and whose section is shown in lavender. The ray is incident along the normal to the stereocilium, the axis of symmetry of the section. For parallel rays further from , the angle of incidence at which the light strikes the stereocilium's surface increases as measured with respect to the normal. These three rays of incident light impart distinct forces on the stereocilium. (B) When a ray is reflected, it forces the stereocilium in the opposite direction and the direction of this input reflection force is radially aligned with the center. (C) If the ray is deflected due to refraction, a deflection force () is generated on the stereocilium that is perpendicular to the direction of the ray as it propagates within the stereocilium. The incident angle is equal to the reflection angle, as is the case for the ray as it first strikes the stereocilium (). The light that is refracted propagates along (orange line) once inside the stereocilium until it reaches the boundary with water. At this second collision the incident angle is equal to the refractive angle , which is too small to cause another reflection; as a result, the ray exits into water and no deflection force is generated. (D) A third kind of force arises if total internal reflection (TIR) occurs, as happens when the angle of the incident light beam is such that a ray remains trapped inside the stereocilium as it is repeatedly reflected at the boundary with water. In the case of ray , the incident angle is equal to the critical angle for total internal reflection—72° in this case—and the light remains within the stereocilium as (blue arrow) and is reflected repeatedly each time it reaches the boundary with water. Three successive total internal reflections are shown; each generates a reflection force .