Dynamic spatiotemporal coordination of neural stem cell fate decisions occurs through local feedback in the adult vertebrate brain

Summary

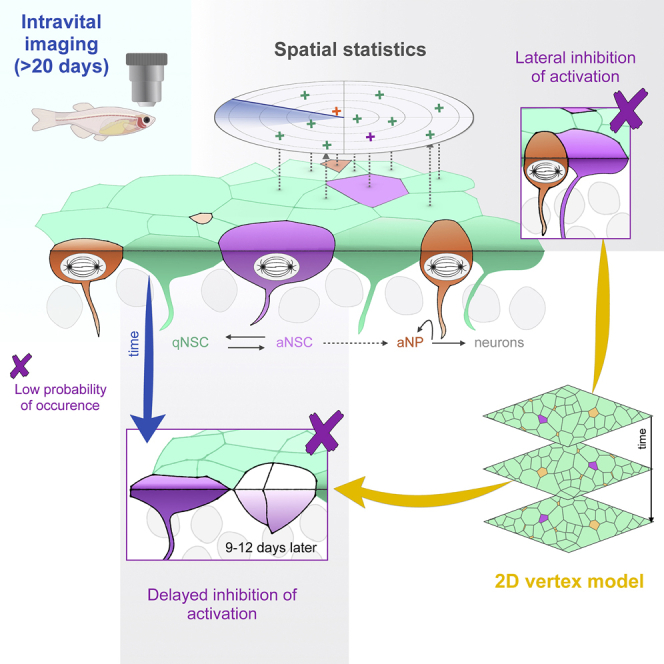
Neural stem cell (NSC) populations persist in the adult vertebrate brain over a lifetime, and their homeostasis is controlled at the population level through unknown mechanisms. Here, we combine dynamic imaging of entire NSC populations in their in vivo niche over several weeks with pharmacological manipulations, mathematical modeling, and spatial statistics and demonstrate that NSCs use spatiotemporally resolved local feedback signals to coordinate their decision to divide in adult zebrafish brains. These involve Notch-mediated short-range inhibition from transient neural progenitors and a dispersion effect from the dividing NSCs themselves exerted with a delay of 9–12 days. Simulations from a stochastic NSC lattice model capturing these interactions demonstrate that these signals are linked by lineage progression and control the spatiotemporal distribution of output neurons. These results highlight how local and temporally delayed interactions occurring between brain germinal cells generate self-propagating dynamics that maintain NSC population homeostasis and coordinate specific spatiotemporal correlations.

Graphical abstract

Highlights

• •NSC activation events are spatiotemporally coordinated within adult NSC populations
• •This involves inhibition by neural progenitors (relying on Notch) and by dividing NSCs
• •A dynamic lattice model shows that these interactions are linked by lineage progression
• •NSCs dynamics generate an intrinsic niche that maintains the NSC population long-term

Using intravital imaging in the zebrafish adult pallium, Dray et al. analyze the endogenous spatiotemporal activation pattern of NSCs in relation with their neighbors. They demonstrate that transient inhibitory interactions involving NSCs and progenitors along lineage progression generate an intrinsic niche that coordinates NSC recruitment at large scale and long term.

Introduction

The maintenance of organ physiology over a lifetime is permitted by the activity of resident stem cells (SCs). Adult SCs locally generate differentiated progeny for functional plasticity, cell replacement, or organ growth. Adult SCs also self-renew, to ensure their own maintenance. Because differentiation and self-renewal occur concomitantly, the perdurance of SC populations (referred to as homeostasis) is a dynamic process. It remains, however, poorly understood how adult SCs achieve this long-term, dynamic, and spatiotemporal equilibrium.

In adult epithelial systems, SC clonal behavior fits stochastic decisions of gain or loss made among equipotent SCs; thus, SC numbers are maintained at the population level (Greulich and Simons, 2016; Klein and Simons, 2011; Rulands and Simons, 2016). In addition, SC fate choices are controlled in space. the positioning of SC recruitment events will affect the location of progeny cells—hence, organ growth and function. Such population-based homeostasis suggests the existence of feedback control mechanisms coordinating stemness-related fate choices over time (Lander, 2009; Rué and Martinez Arias, 2015) and in space. From the spatial perspective, a prevalent example of coordination was illustrated in mouse interfollicular epithelial SCs, in which the delamination of differentiating SCs triggers the division of neighboring SCs (Mesa et al., 2018). It remains, however, unknown whether these findings can be generalized, in particular to other SC systems with slower turnover than epithelia and where SCs may not be prone to immediate division.

Along these lines, a particularly relevant case is the vertebrate adult brain, in which neural stem cells (NSCs) are mostly quiescent, with an average of one recruitment event every few weeks or months (Basak et al., 2018; Than-Trong et al., 2020; Urbán et al., 2019). In addition to a generally deep location inside the brain, this makes NSC pools very difficult to study dynamically in situ (Pilz et al., 2018). In niches of the adult pallium in zebrafish and mouse (sub-ependymal zone of the lateral ventricle [SEZ], sub-granular zone of the dendate gyrus [SGZ]), NSCs are apico-basally polarized astroglial cells, arranged in neuroepithelium-like assemblies from which their neuronal progeny emigrates (Gonçalves et al., 2016; Obernier et al., 2018; Than-Trong and Bally-Cuif, 2015). NSCs can stochastically choose distinct fates, whose equilibrium is maintained through population asymmetry (Basak et al., 2018; Than-Trong et al., 2020). However, we lack an integrated spatiotemporal understanding of NSC population behavior and of how their homeostasis can be dynamically maintained in time and space long term.

To address this issue, we made use of the everted organization of the adult zebrafish pallium, in which NSCs are organized as a dorsally located ventricular monolayer (Adolf et al., 2006; Grandel et al., 2006). Using transparent adult mutants and transgenic backgrounds reporting NSCs or cell states, it is possible to image NSCs in their niche and reconstruct their behavior over weeks (Barbosa et al., 2015; Dray et al., 2015). We applied it here to reconstruct the tracks of all NSCs within entire portions of the dorsal pallium and study, at the population level, the spatiotemporal regulation of the most upstream NSC fate decision: activation. Activation is the transition from the quiescent to the proliferating state, and signals NSC recruitment. In the zebrafish adult pallium at any given time, NSC activation events are broadly distributed across the entire NSC pool (Dray et al., 2015). Using long-term intravital imaging of the dorso-medial pallium (Dm), we reveal that NSC activation events are not randomly positioned but respond to cell-cell inhibitory cues that operate over space and time within the NSC pool. From quantitative experimental parameters, we develop a mathematical modeling platform that faithfully recapitulates NSC population behavior and demonstrate that the spatiotemporal dynamics and propagation pattern of NSC recruitment events is an emergent property of lineage cues. These analyses provide the first quantitative understanding of spatiotemporal homeostasis in adult vertebrate NSC pools.

Results

NSC activation events are randomly positioned relative to each other across the NSC population at any given time

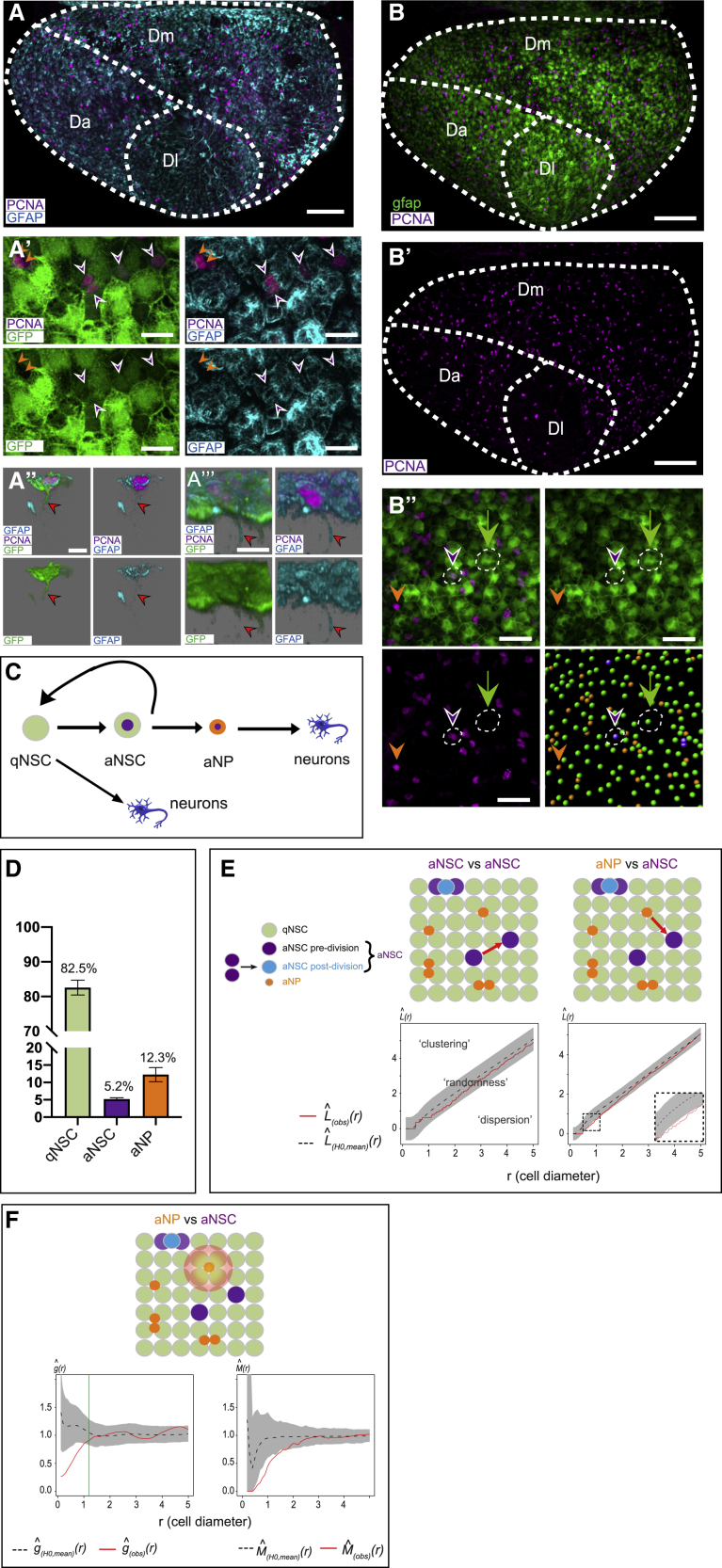
Adult pallial NSCs in zebrafish and rodents are radial glial cells expressing glial fibrillary acidic protein (Gfap) (Ganz et al., 2010; März et al., 2010). Whole-mount immunostaining for GFP in Tg(gfap:gfp) transgenic adults (Bernardos and Raymond, 2006) (3 months post-fertilization, mpf) is a faithful reporter of Gfap expression, as demonstrated by the strict co-labeling of GFP and Gfap proteins (Figures 1A–1A’’). Together with the proliferating cell nuclear antigen (PCNA) and the progenitor marker Sox2, it reveals the distribution of proliferating cells at large scale within the pallial NSC pool (Figures 1B–1B’’ and S1), and three essential ventricular cell states/types (referred to as “states”): quiescent NSCs (qNSCs) in the G0 state (GFAP⁺;Sox2⁺;PCNA⁻), activated NSCs (aNSCs) in G1-S-G2-M (GFAP⁺;Sox2⁺;PCNA⁺), and activated neural progenitors (aNPs) (GFAP⁻;Sox2⁺;PCNA⁺). These cells are lineage related (Figure 1C). qNSCs activate periodically and can return to quiescence, while aNPs are generated by symmetric or asymmetric neurogenic divisions of aNSCs, and will delaminate from the germinal sheet to generate neurons (Rothenaigner et al., 2011; Than-Trong et al., 2020). At any time, aNSCs make up 5.2% of the entire progenitor population in Dm (NSCs + aNPs), against 82.5% qNSCs and 12.3% aNPs (Figures 1D and S1A–S1A’’; Table S1).

Figure 1.

Inhibitory interactions between progenitor cells bias the distribution of NSC activation events

(A–A’’') Confocal dorsal views of a whole-mount adult telencephalon showing the germinal layer of the pallium in a 3mpf Tg(gfap:GFP) fish immunostained for GFP (green, NSCs), PCNA (magenta, proliferating cells), and Gfap (Zrf1 antibody, cyan). Anterior left, pallial subdivisions (Dl: lateral, Dm: medial, Da: anterior) indicated by dotted lines.

(A and A’) Dorsal (apical) view and high magnification of the NSC layer, showing merged and single channels (color-coded). Arrowheads: purple to aNSCs, orange to aNPs. aNSCs are GFP⁺,Gfap⁺, aNPs are negative for both markers.

(A’’ and A’’’) Examples of aNSCs with a process (red arrows) visible using the GFP or the Zrf1 markers, respectively (left and right panels: different backgrounds to ease observation).

(B–B’’) Similar sample stained for GFP (green, NSCs) and PCNA (magenta, proliferating cells).

(B and B’) Merged and single-channel views (color-coded).

(B’’) Close-up in Dm showing progenitor cell states (merged image, individual channels and segmentation): quiescent NSCs (qNSCs; GFP⁺ only; green), activated NSCs (aNSCs; GFP⁺,PCNA⁺; magenta), and proliferating neural progenitors (aNPs; PCNA⁺ only; orange) (see also Figures S1A–A”).

(A, B, and B') Stitches of 4 tiles with 10% overlap.

(C) Main pallial NSC lineage (arrows: lineage transitions).

(D) Proportions of qNSCs, aNSCs, and aNPs relative to each other in Dm (see also Figures S1B–B’’’).

(E) Besag’s L function assessing spatial correlations for the same fish between aNSCs (left) and between aNSCs and aNPs (right) (aNSCs include pre-division aNSCs—singlets—and immediately post-division NSCs—doublets, scheme on left). L_(obs)(r) (red line): experimental value, L_{(H0, mean)}(r) (black dotted line): mean under the random labeling null hypothesis (the state of any cell is independent of other cells and of its position), r: mean cell diameter in this brain (r = 0: cell of reference, r = 1: immediate neighbor), gray regions: 95% confidence envelopes. High magnification shows significant dispersion (see also Figures S2A–S2E).

(F) Range and strength of this interaction determined with functions g (left) and M (right). Green bar: 95^th centile of the distance to the furthest direct neighbor of aNPs.

Scale: (A), (B), and (B’) 100 μm; (A’) 10 μm; (A’’), (A’’’) 7 μm; (B’’) 30 μm.

The detection of every individual cell based on the position of its nucleus, located apically, generates an array of spatial coordinates that captures the position and state of each cell (Figures 1A–1A’’’). Full-scale maps plotting local cell densities, cell states, and their ratio highlighted strong differences between pallial subdivisions but similarities between hemispheres in individual fish (Figures S1B–S1B’’’), as well as between fish. This argues for the reliability of our whole-mount detection approach and stresses the need to focus on individual pallial subdivisions to avoid statistical flaws due to spatial heterogeneities. In the remainder, we analyzed Dm, in one hemisphere per animal.

To determine whether NSC activation events respond to specific spatial rules, as opposed to uniquely cell-autonomous decisions, we described their distribution within the NSC population. Because the PCNA protein is detected throughout the cell cycle in this system, including shortly post-M phase, some PCNA⁺ signals mark post-cytokinesis pairs of sister cells, which are to be considered as a single recent NSC activation event. We found that sister NSC pairs, labeled by a bromodeoxyuridine (BrdU) pulse, accounted for virtually all of the aNSC doublets (GFAP⁺;PCNA⁺) after a 18- to 24-h chase (Figure S1C–S1C’’). Morphologically, NSC sisters appeared tightly juxtaposed and symmetrical Figures S1C’ and S1D). Such aNSC doublets were segmented as a single activation event (Figure S1E). We next used spatial point pattern analyses (Baddeley et al., 2016) to test for spatial interactions between NSC activation events (Figure S1A; Method details). We tested whether aNSCs were randomly distributed relative to one another at the same time point. To detect spatial correlations, we used Besag’s L functions (Besag, 1977), a variance-stabilized version of Ripley’s K function (Ripley, 1977) with an isotropic edge correction. If a spatial interaction was detected, then we turned to two second-order functions, g and M (Figure S2A). The pair correlation function g is a rescaled derivative of the K function, necessary to determine the interaction range. The M function (Marcon and Puech, 2010; Marcon et al., 2012) is an extension of the K function adjusted for cell frequencies across the Dm domain, offering easily interpretable values to quantify interactions. The locations of aNSCs were compared with a random distribution under the random labeling null hypothesis, obtained by permuting the same number of aNSCs among the experimental number of NSCs (qNSCs + aNSCs) for each fish (Figure 1E). In each case, the 95% confidence envelopes delimit a pattern in which the distribution of aNSCs is considered random, as opposed to clustered or dispersed (Figure S2A). In all of the cases, the distribution of aNSCs relative to one another was found within the random interval (Figures 1E, S2B, and S2C). The same was obtained when pre-cytokinesis activation events (aNSC singlets) were positioned relative to post-cytokinetic aNSCs (doublets) (Figure S2D). Thus, at any given time, NSC activation events are spatially independent from one another.

NSC activation events are locally inhibited by committed progenitors

Because aNPs could also provide positional cues, we assessed aNSCs relative to aNPs, using Besag’s L function, after segmenting aNPs in each specimen. This experimental distribution was challenged against simulations in which the same number of aNSCs is randomly permuted among all of the NSCs, while aNPs are maintained at their endogenous position. In this case, we observed a deviation from the random pattern, aNSCs being further away from aNPs than expected by chance (Figures 1E and S2E).

To further characterize the range and strength of this effect, we used Ripley’s g and M functions, respectively (Marcon and Puech, 2010; Marcon et al., 2012). Ripley’s g function revealed a statistically significant shift of aNSC positioning relative to aNPs for radiuses within 1 cell diameter (Figure 1F), indicative of short-range interaction. It fell within the random chance boundaries for distances beyond the furthest direct neighbor. Within a 1-cell diameter distance, Ripley’s M function revealed an interaction strength of 0.25–0.5 between aNSCs and aNPs, showing that aNSCs are found next to aNPs 2–4 times less frequently than expected by chance (Figure 1F). All four animals studied showed the same interactions (Figure S2E). Thus, at any given time, NSC activation events tended to avoid the immediate neighborhood of aNPs.

The lower number of NSC activation events close to aNPs is Notch signaling dependent

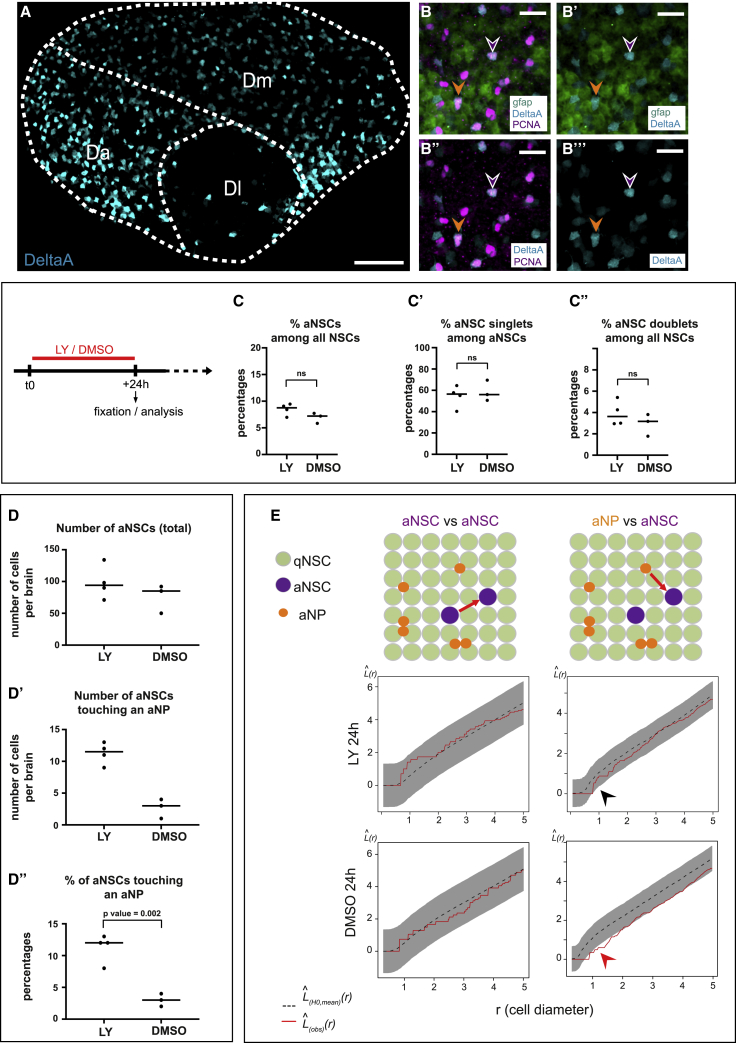
Several hypotheses could account for aNSCs being less frequent next to aNPs: an accelerated delamination of aNPs next to aNSCs, a tangential displacement of aNSCs and aNPs away from each other, and/or an inhibition of NSC activation by aNPs. The z distance of aNP nuclei from the ventricular surface—an indication of their delamination—showed no relation to their proximity to aNSCs (Figure S3A). To evaluate aNP tangential migration, we clonally labeled individual NSCs in 3mpf adults, followed by a short chase. Focusing on clones containing one or a few aNPs and a single NSC, we found no tangential displacement of aNPs from their NSC of origin (Figures S3B–S3B”). NSCs themselves are stable relative to one another (Dray et al., 2015). These results rule out the frequent occurrence of tangential rearrangements. Finally, we focused on NSC activation. In the adult zebrafish pallium and mouse SGZ, Notch3 signaling promotes NSC quiescence (Alunni et al., 2013; Kawai et al., 2017), and aNPs express the Notch ligand DeltaA (Chapouton et al., 2010). Here, we quantified that 99% of aNPs (and 86% of aNSCs) express the deltaA:egfp transgene at any time (Figures 2A and 2B). DeltaA:egfp⁺ cells also display horizontal extensions over a few cell diameters (Figure S3C) (Obermann et al., 2019). Thus, aNPs may locally affect aNSCs via Notch signaling.

Figure 2.

The lower incidence of activated NSCs close to aNPs is Notch signaling dependent

(A) Confocal whole-mount view of the pallial germinal layer in a 3mpf Tg(gfap:tdTomato);Tg(delta:GFP) fish stained for tdTomato (NSCs, green), GFP (deltaA expression, cyan) and PCNA (magenta) (DeltaA channel only). Anterior, left. (A) Stitch of 4 tiles with 15% overlap.

(B–B’’’) Close-ups in Dm, all channels. Arrowheads: magenta, aNSC; orange, aNP; expressing deltaA.

(C–C’’) Percentages of aNSCs (all, pre-, or post-division) among all NSCs (C and C”) or aNSCs (C’) upon 24-h LY treatment (DMSO: control). ns, non-significant; unpaired t test (see also Figures S2F, S3A–S3C, and S4A–S4B’’).

(D–D”) Number (D and D’) and proportion (D’’) of aNSCs, in total (D) or touching aNPs upon 24-h LY treatment (DMSO: control) (D’’, p = 0.002, t test) (see also Figure S3C).

(E) Spatial distribution (Besag’s L function) of aNSC singlets relative to each other (left) and to aNPs (right) upon 24-h LY treatment (DMSO: control). L_(obs)(r) (red lines): experimental values; L_(H0,mean)(r) (black dotted lines): means under the random labeling null hypothesis; r: mean NSC diameter; gray regions: 95% confidence envelopes. Arrowheads: red, aNP inhibitory effect; black, disappearance upon LY (see also Figures S4C–S4F).

Scale: (A) 40 μm, (B)–(B’’’) 20 μm.

To conditionally decrease Notch signaling, we subjected 3mpf adults to a 24-h treatment with the gamma-secretase inhibitor LY411575 (LY) (Alunni et al., 2013). This short treatment strongly downregulates the expression of the Notch target gene her4 (Figures S4A and S4B), validating its efficiency. However, it minimally affects cell fate/state; it only partially reactivates NSCs (6.9% aNSCs among all NSCs in DMSO-treated versus 8.5% in LY-treated animals, and comparable proportions of singlets and doublets) (Figure 2C) and is too short for most aNPs to differentiate (9.1% aNPs in DMSO-treated versus 10.8% in LY-treated animals) (Table S1). To further control that LY did not affect aNP fate/state and distribution, we compared the position of aNPs relative to one another in LY-treated versus DMSO-treated animals (Figures S4C and S4F). In all of the cases, aNPs appeared clustered at short range, with 2–5 times more aNPs within a 1-cell diameter range than expected by chance. This result reflects rapid amplifying divisions by a fraction of aNPs, generating small clusters before differentiation (Figure S1D). Neither this pattern nor its range and strength were affected by LY.

The chosen LY treatment length is also typically shorter than the NSC cell-cycle duration (Figures S1C–S1C’’); thus, to focus on activation events initiated during treatment, we considered in this case only aNSC singlets. We observed that the number and proportion of aNSCs in contact with an aNP was increased upon LY treatment (Figure 2D). Next, Besag’s L, Ripley’s g, and Marcon and colleagues’ M functions confirmed the short-range inhibition exerted by aNPs in all DMSO-treated controls (Figures 2E, bottom right, and S4E, bottom), but this inhibition was abolished upon LY treatment (Figures 2D and 2E, top right, and Figure S4E, top). Notch blockade was, in contrast, without effect on the random pattern of aNSCs relative to one another (Figures 2E, left panels, and S4D). This is compatible with a model in which, at any given time, the spatial positioning of NSC activation events responds, directly or indirectly, to short-range Notch-dependent inhibitory cues exerted by aNPs.

NSC activation events are spatially controlled over time by preceding spatial activation patterns

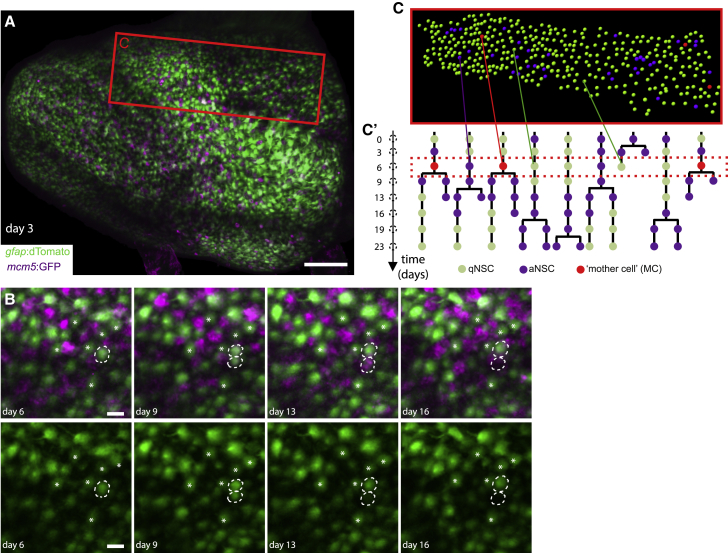
We next addressed whether the spatial pattern of NSC activation events incorporates temporal information. Previous results indicate that the majority of aNSCs return to quiescence after division (Than-Trong et al., 2020). Thus, aNSCs observed at a few days’ interval reflect the successive activation of different qNSCs (Alunni et al., 2013). Using intravital imaging (Dray et al., 2015), we recorded NSCs in 3mpf transparent double-mutant casper adults, double transgenic for gfap:mTomato (NSCs) and mcm5:egfp (activation events), in their endogenous pallial niche over a minimum of 23 days at 3–4 days’ interval (Figures 3A and 3B). In each animal (n = 3), the position of every NSC of a complete ensemble of 370–500 neighboring NSCs was detected, and videos were assembled to reconstruct the behavior of every cell (Figures 3C and 3C’; Video S1). Hence, lineage trees (referred to as “tracks”) could be produced for each NSC (Figures 3C’, S5A, and S5B; Table S2). As expected, given the slow dynamic of the system, most cell tracks were silent during the 3–4 weeks of recording: on average, 117 over 1,203 tracks captured (9.7% ± 0.8%) led to at least a division event (Figure S5C). Most important, because we recorded every NSC of the population, these events were spatiotemporally resolved relative to neighboring cells (Figures 3C and 3C’), providing a complete 4D dataset of NSC population behavior in situ. Due to relatively weak mcm5:egfp staining, we could not efficiently resolve aNPs, which were therefore not considered in the dynamic analysis.

Figure 3.

Intravital imaging resolves adult NSC lineage trees in time and space

(A) Whole pallial hemisphere imaged intravitally in a 3mpf casper;Tg(gfap:dTomato);Tg(mcm5:GFP) fish (named Mimi) (anterior left, tile of 4 images with 10% overlap, taken at day 3 from a 35-day session of recordings every 3–4 days, 8 time points). Colors of the live reporters were adjusted (green: NSCs, magenta: proliferating cells).

(B) Close-ups from the same video showing an asymmetric NSC division (dotted circles) between days 3 and 9: 1 daughter differentiates over the next 7 days (bottom dotted circle, loss of the gfap:dTomato signal). White asterisks: random qNSCs close to the division, used for alignment.

(C and C’) Segmentation and NSC tracking over 23 days in Dm in Mimi. (C) Segmentation of ~390 cells per time point (area boxed in A, at day 6). (C’) Example of dividing tracks, with cell states (color-coded) and the spatial position of each tree (see also Figure S5A). Scale bars: (A), 100 μm; (B), 20 μm.

Video S1. 3D animated rendering of the intravital imaging, related to Figures 3, 4, and 5

Whole pallial hemisphere of Titi (casper;Tg(gfap:dTomato);Tg(mcm5:GFP)) (anterior left), with blow-up of the tracked region (white dots: tracked cells; green -qNSC- and magenta -aNSC- spots: 4 tracks with divisions) and 8 successive time points (-d0 to d23-, white arrowheads: division events).

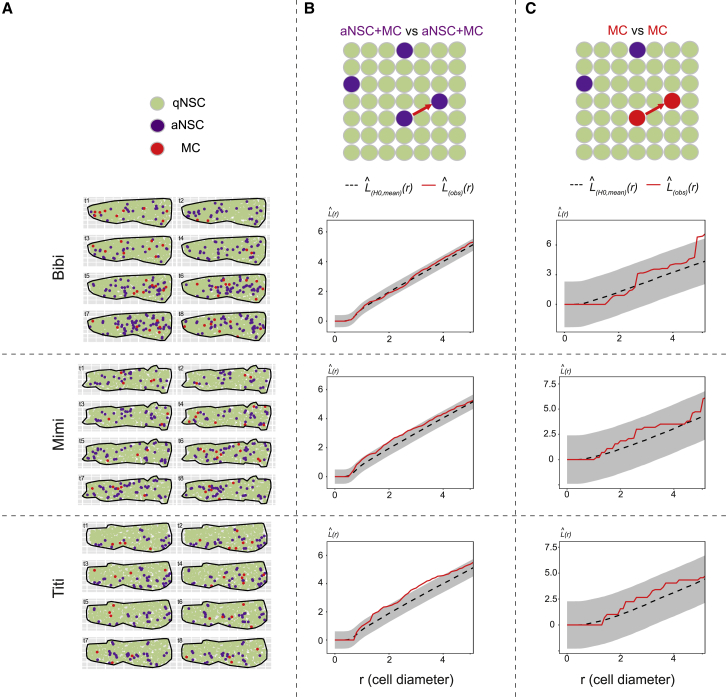
We tested whether this approach could recapitulate the results obtained on the static pattern of aNSC placement. We focused on de novo activations (first division of a track) and the Mcm5⁺ period preceding and during division (Figures S5D–S5F; Table S2), and applied a point pattern analysis at every individual time point to address the relative position of activation events within the whole NSC population. These events were found randomly positioned relative to each other (Figures 4A and 4B). This analysis further revealed that the NSC activation phase can span several consecutive time points before division. The NSC-activated phase fits an exponential decreasing function with a decay rate of 0.22 day⁻¹, corresponding to a mean aNSC half-life of 3.2 days (Figure S5G). Thus, in the following, we focused on the more temporally restricted event of cell division proper, reflecting the NSC recruitment event affecting cell fate (“mother cell” state [MC], defined as the imaged time point immediately preceding cell division) (Figures 3C, 3C’, 4, and S5A, red cells). MC events also appeared randomly positioned relative to one another at any time (Figure 4C).

Figure 4.

Static spatial analysis of NSC activation from dynamic datasets

(A) Dm surfaces segmented for the 3 fish analyzed (Bibi, Mimi, Titi) at all time points, cell states color-coded (see also Figures S5B–S5F).

(B and C) L functions comparing the positions of aNSCs+MCs with one another (B), and MCs with one another (C) for each fish (see also Figures S5A–S5F). L_(obs)(r) (red lines): experimental values, L functions for all time points pooled using a weighted average; L_{(H0, mean)}(r) (black dotted lines): means under the random labeling null hypothesis; r: mean NSC diameter for each Dm surface; gray regions: 95% confidence envelopes. Pooled p > 0.01 in (B) and (C) for the [0–2] (r) interval.

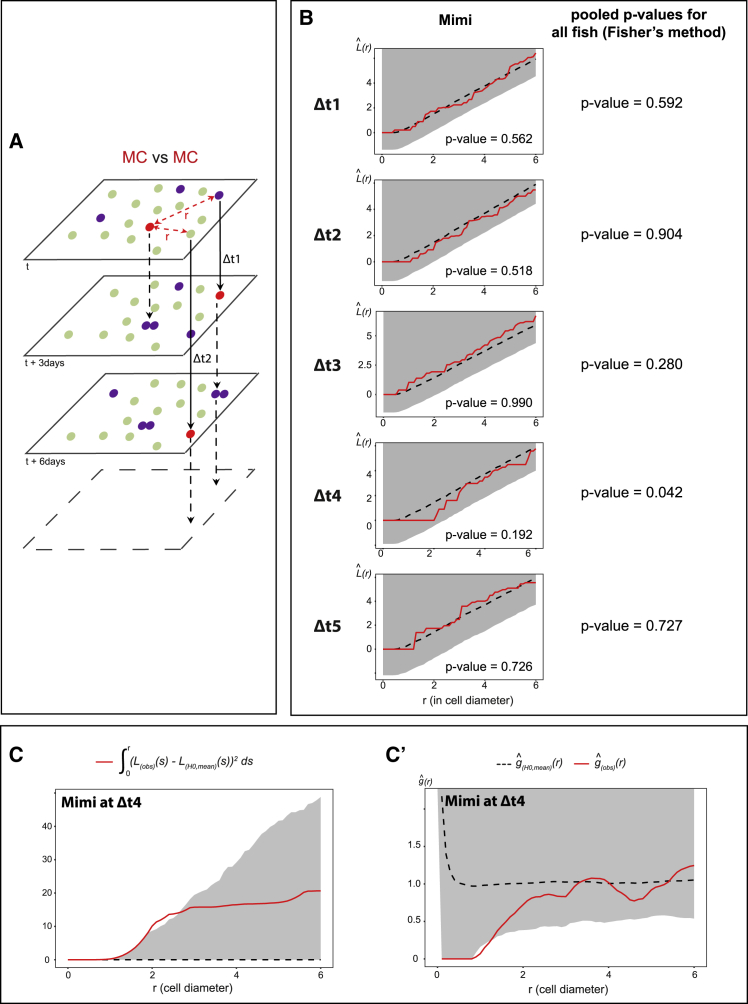
To probe for temporal correlations, we tested whether MC positioning was influenced by the distribution of MCs at previous time points. In a point pattern analysis across time, we measured the position of MCs relative to MCs at earlier imaging days at all possible time intervals (e.g., Δt1: 1 imaging time point = 3 days, Δt2: 2 time points = 6 days), and compared this to a scenario in which the distribution of MCs at time t is random within all NSCs (Figure 5A). This revealed a trend dispersion from the random distribution at Δt4 (9–12 days) (Figure 5B). This trend is visible in all fish, is not observed at any other time interval, and reaches significance when pooling the 3 fish analyzed (>1,200 cells per time point in total) (Figure 5B). Besag’s L integrated squared deviation and Ripley’s g function further indicate an effect exerted at a 1- to 2-cell diameter range (Figures 5C and 5C’). Thus, the positioning of NSC division events incorporates spatiotemporal information with a delay, being less frequent within a radius of 1- to 2-cell diameter from the position occupied by dividing NSCs 9–12 days before.

Figure 5.

NSC division events are spatiotemporally coordinated

(A) MC positions at time point t are compared, using point pattern statistics, with MC positions at other time points after fixed intervals (t+Δt), for each possible Δt (3, 6, 9, and 15 days).

(B) Left: Besag’s L functions comparing MCs with one another for all Δt intervals in Mimi (see also Figures S5A–S5E). L_(obs)(r) (red lines): experimental values; L_(H0,mean)(r) (black dotted lines): means under the random labeling null hypothesis; r: mean NSC cell diameter for each Dm surface: gray regions: 1-sided 95% confidence envelopes. Each fish shows a trend dispersion at Δt4. Right: combined p values for Mimi, Bibi, and Titi (Fisher’s method) (significant at Δt4).

(C and C’) Illustrations for Mimi. (C) Integrated square of the negative deviation between L_(obs)(r) and L_{(H0, mean)}(r) (surface under L_{(H0, mean)}(r)) at Δt4. (C’) Ripley’s g function indicating an effect at the nearest neighbor’s range.

A mathematical model of NSC behavior reveals the influence of population feedback in the spatiotemporal control of NSC activation and division events

The results above show that de novo NSC activation and division events follow spatiotemporal correlation rules encoded by the NSC/NP population. They are disfavored in the immediate vicinity of aNPs at all times, and, with a temporal delay of 9–12 days, in territories neighboring the position of previous NSC division events.

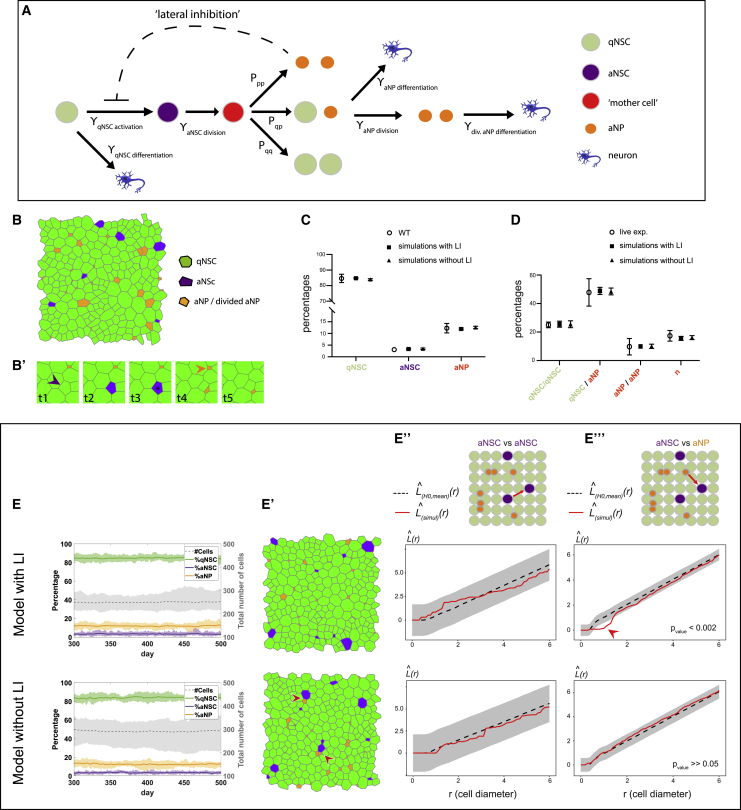
To gain insight into whether these events were linked and whether they reflected bona fide instructive cues as opposed to emergent cues from the NSC ensemble, we developed a stochastic spatiotemporal model of NSC behavior (NSC lattice model). The model is constructed in two layers to faithfully incorporate experimental data. The first layer enables analytical estimation of the system’s dynamic parameters to be used in the second layer, itself enabling stochastic simulations and spatiotemporal analysis of the system over time (Methods Figure S1A; Method details). Because NSC numbers are constant within a tracked NSC population (Than-Trong et al., 2020)—a finding verified here (Figure S5E)—the first layer is an analytical steady-state mean field analysis of dynamic rate equations describing the transitions between the different progenitor cell states and differentiated neurons (Figure 6A and Methods Figure S1A, left). This analysis identifies the transition rates (γ parameters) based on quantitative experimental data, which include (Figures S5G–S5K’’) the proportions of qNSCs, aNSCs, and aNPs at steady state; the duration of the NSC activation phase; division frequencies; and spatial information on the number of qNSCs in contact with aNPs. These rates are used as input for the second layer (Methods Figure S1A, right), which uses spatial stochastic simulations to obtain insight into the spatiotemporal correlations between the different cell states. It uses a 2-dimensional (2D) vertex modeling platform to simulate the transition between cell states, cell divisions, and cellular differentiation in a disordered cell lattice (Figures 6B and Methods Figures S1B–S1D). Cellular morphologies are determined by minimizing mechanical energy following these events (Methods Figures S1E–S1G).

Figure 6.

An NSC lattice model captures NSC population dynamics

(A) Model lineage flowchart. γ: transition rates; P_qq, P_qp, and P_pp: probabilities for (as)symmetric aNSC divisions; dashed line: lateral inhibition (LI) of aNPs on NSC activation (see also Figures S5G–S5K’’ and Methods Figure S1).

(B and B’) Snapshot of the lattice (B) and (B’) examples of activation (purple arrowhead), division (black star), and differentiation (orange arrowhead) (Video S2).

(C and D) Average cell proportions (C) and (D) percentages of cell fates following cell division in sets of 18 simulations with and without LI versus in vivo.

(E–E’’’) Dynamics and spatial correlations from the NSC lattice model with (top) and without (bottom) aNP-driven LI.

(E) Stable cell numbers and proportions over time, matching experimental data. Bold line: mean; shaded area: range; n = 18 simulations..

(E’) Snapshots of the lattice at 1 time step from a simulation of 500 time steps. Red arrowheads: aNSCs neighboring aNPs.

(E’’ and E’’’) Besag’s L function of aNSCs relative to one another (E’’) and to aNPs (E’’’). Results of a representative simulation are shown (1 from each model). L_(simul)(r) (red lines): simulated values; L_(H0,mean)(r) (black dotted lines): means under the random labeling null hypothesis; r: mean cell diameter (distance is measured from cell’s center); gray regions: 95% confidence envelopes. Red arrowhead to the dispersion of aNSCs from aNPs at a range of 1- to 2-cell diameter with LI. Cutoff for p values in E’’’ = 0.05.

The stochastic simulations also incorporate the aNP-mediated feedback inhibition on aNSCs. We considered an inhibition of NSC activation (referred to as lateral inhibition [LI]) and encoded it by suppressing the transition from qNSC to aNSC when the qNSC is in direct contact with an aNP (dashed line in Figure 6A). To be able to compare the spatiotemporal distributions between models with and without LI, we adjusted the two models so that their average cell populations are the same (i.e., same qNSC, aNSC, and aNP proportions) by introducing a constant factor, I ≤ 1, multiplying the qNSC activation rate (I = 1 without LI and I < 1 with LI). This factor compensates for the overall mean field effect of LI so that the effective qNSC activation rate is similar in both models. I with LI is estimated from the average fraction of qNSCs that are not in contact with any aNP (Figures S5K–S5K’’). Long-term simulations with and without LI showed that stability is reached within tens of days when starting from random initial distributions. Simulations analyzed between days 300 and 500 showed the maintenance of steady-state proportions of cell states and total cell numbers (Figure 6E), as well as average cell sizes and number of neighbors (Video S2). The qNSCs, aNCs, and aNPs fractions at steady state, and the percentages of cell divisions or direct differentiation, match experimental measures (Figures 6C–6E). These simulations also recapitulated the spatial bias in aNSC distribution relative to aNPs at any time, with similar range and strength as observed in vivo, in the model run with but not without LI (Figures 6E, 6E’, and 6E’’’). All of the other static spatial correlations uncovered in vivo were also observed. aNSCs appear randomly positioned relative to one another at any time, and aNPs appear locally clustered due to their rapid divisions (Figure 6E”; data not shown).

Video S2. NSC lattice model simulations with and without LI over 200 time steps, related to Figures 6 and 7

One representative simulation out of 18 for each model, showing state and morphological changes.

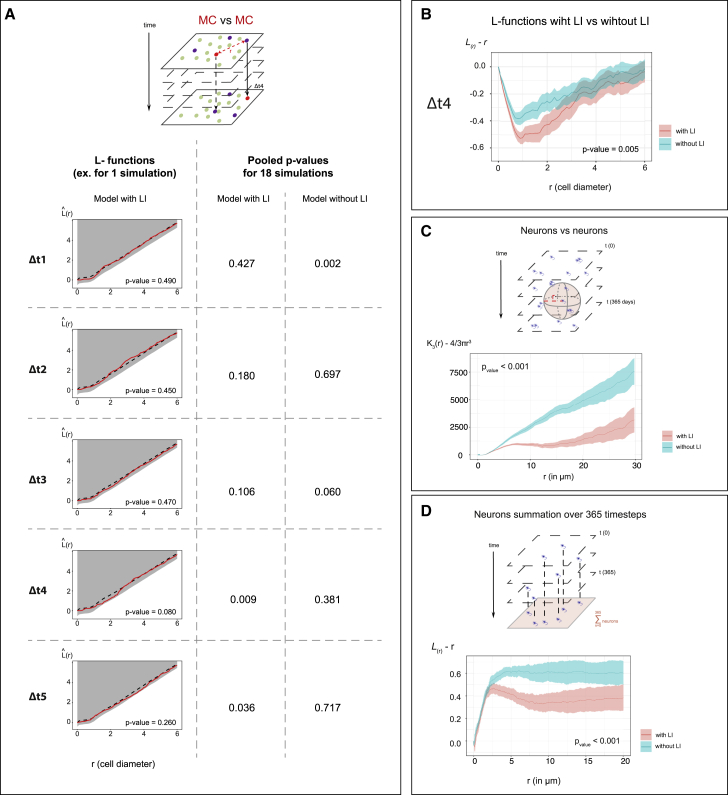
Next, we used the NSC lattice model to shed light on the origin and determinant parameters of the delayed effect of MCs on future MC events. This could reflect an active action of MCs or emerge from the spatiotemporal characteristics encoded in the NSC lattice model. We estimated Besag’s L function in multiple simulations with and without LI and quantified the correlation between the position of MCs relative to one another across a range of Δt intervals similar to the in vivo analysis (Figure 7A). We found a statistically significant dispersion of MCs relative to one another with time intervals of Δt4 = 9–12 days in the model with LI compared to a random distribution (Figure 7A). We next showed that this effect at Δt4 statistically differed from the model without LI, by comparing the L functions for all pairs of MCs separated by an interval of Δt4, with versus without LI, using a permutation test (Hahn, 2012) (Figure 7B). Thus, the parameters encoded into the lattice model, and in particular the aNP-driven LI, are sufficient to generate spatiotemporal interactions between MC events that resemble, in their delayed effect and inhibitory output, those detected in vivo. To further support a conclusion linking the generation of aNPs with MC interactions over time, we ran additional simulations after modifying the aNP half-life to accelerate their progression along lineage commitment (specifically, we reduced the aNP lifetime by 25%; Figure S6A). This model also showed stability in cell type proportions and correctly captured the aNP-mediated inhibitory effect on aNSCs at any time (Figures S6A’ and S6A”), but predicted spatiotemporal MC interactions at a time interval of Δt3 (6–9 days) rather than Δt4 (Figure S6A’’’). Thus, the temporal delay in MC-MC interactions is linked to the speed of lineage progression.

Figure 7.

The NSC lattice model reproduces the spatiotemporal correlations of NSC fate decisions and shows their impact on long-term neuronal distribution

(A) Top: MC positions at any time t in the lattice model are compared using point pattern statistics with MC positions at t+Δt. Bottom left: Besag’s L functions assessing the spatial interaction of MCs relative to one another at all Δt intervals in 1 representative simulation with aNP-driven LI. L_(simul)(r) (red lines): simulated values; L_(H0,mean)(r) (black dotted lines): means under the random labeling null hypothesis; r: mean NSC cell diameter (distance measured from cell’s center); gray regions: 1-sided 95% confidence envelopes. Bottom right: combined p values (Fisher’s method) of Besag’s L functions for a model with (left) versus without (right) LI (18 simulations each). A significant p = 0.009 is obtained with Δt4. Cutoff for pooled p = 0.01.

(B) Compared L functions (lines) and their 95% confidence intervals (shaded) testing for dispersion between MCs at Δt4 in a model with (pink) and without (blue) LI (18 simulations each). Cutoff for pooled p = 0.01 (see also Figures S6 and S7).

(C) Compared spatial interaction between output neurons in a model with (pink) and without (blue) LI, using a 3D Ripley’s K function on 18 simulations in each model, analyzed during 365 time steps (shaded area: confidence intervals). The positions were evaluated in microns by comparing between the simulated and experimental cell’s mean diameter (lattice plane) and using a neuron’s layer generation rate 30 μm/2 months (time axis) (Than-Trong et al., 2020).

(D) Similar comparison (to C) in 2D, using the L function. At each time step, the neurons are projected on a 2D plane parallel to the lattice surface and accumulated from 365 time steps.

(B)–(D) show centered summary functions, K₃(r) − (4/3)πr³ and L(r) − r, rather than raw functions, to highlight differences. p < 0.001: Studentized permutation tests comparing the values of the K and L functions. Cutoff for p values in (C) and (D) = 0.01.

As an alternative mechanism that could lower aNSCs near aNPs, we also considered that aNPs may increase the aNSC division rate. We encoded an alternative model in which aNPs trigger neighboring aNSCs to divide at the immediate next time step (Figure S6B). Such a feedback could also recapitulate the local decrease of aNSCs close to aNPs at any time (Figures S6B’ and S6B”), but, within the limit of our current simulations, it appeared sub-optimal to recapitulate the delayed MC-MC inhibition (Figure S6B’’’). Thus, a local inhibitory effect of aNPs on NSC activation appears to better fit the experimental observations.

The spatiotemporal dynamics of NSC recruitment support more homogeneous neurogenesis output

Finally, we probed the long-term physiological relevance of the uncovered spatiotemporal coordination of NSC dynamics. In the adult pallium, neurons are regularly produced along the medio-lateral and antero-posterior axes and progressively stack in age-related layers ventro-dorsally, generating a homogeneous distribution in 4D (Furlan et al., 2017). To assess the relevance of NSC coordination mechanisms in the long-term generation of this pattern, we ran simulations over 365 days (1 year), and extracted the predicted positions of neurons at all time points. Using a studentized permutation test (Hahn, 2012), the comparison of 3D Ripley’s K functions between simulations showed that the positions of neurons were significantly less clustered in the presence versus absence of LI (Figure 7C) (p < 0.001), most notably between 5 and 20 μm. Thus, coordinating NSC activation strongly affects the spatiotemporal distribution of pallial neurons in 3D.

The pallium, including Dm, is also composed of distinct neuroanatomical units along the medio-lateral and antero-posterior axes (Ganz et al., 2014). To address the role of the spatiotemporal coordination of NSC activation in relation to these units, we reduced the dataset to 2D by projecting neuronal layers into a monolayer parallel to the dorsal pallial surface. Again, neurons were significantly less clustered under conditions with versus without aNP-driven LI (Figure 7D). Thus, an important output of the spatiotemporal control of NSC recruitment by population-derived cues is to spatially homogenize neuronal production long-term across all pallial dimensions.

Discussion

This work addresses the key issue of long-term NSC population homeostasis from the perspective of space and time. We show that the spatiotemporal pattern of NSC activation events is coordinated by local interactions inherent to the NSC pool and identify the qualitative, quantitative, molecular, and functional attributes of the feedback process involved. We also reveal how the transient nature of signaling cells, their downstream position in the NSC lineage, and their effect on adjacent cells generate a dynamic and propagating process ensuring NSC population homeostasis long term and at large scale.

An “in vivo to modeling” cross-talk to study the spatiotemporal control of adult NSC decisions

Analyzing the spatiotemporal dynamics of adult NSC populations is challenging because (1) it requires the preservation of NSC arrangements in their physiological niche, (2) it involves recording the behavior of each individual NSC and its neighbors, and (3) it faces the extremely slow dynamics of NSC fate decisions, with quiescence times over months. To date, intravital imaging was applied to record temporal fate choices in some individual cells (Barbosa et al., 2015; Dray et al., 2015; Pilz et al., 2018; Than-Trong et al., 2020). Here, we tracked an entire NSC population and spatially resolved the state of all NSC states and lineage trees over time. The Dm germinal zone encompasses domains homologous to the SEZ and SGZ (Labusch et al., 2020). Both species also share lifespans, astroglial NSCs organized in tight pools (März et al., 2010; Mirzadeh et al., 2008; Moss et al., 2016; Seri et al., 2004), similar durations of NSC quiescence, and compatible NSC clonal dynamics (Basak et al., 2018; Than-Trong et al., 2020; Urbán et al., 2016), stressing the general scope of our findings. We further exploited this experimental tool to develop a modeling platform based on stochastic simulations on a cell lattice. This model captures the cellular and regulatory processes underlying the adult NSC population dynamics, elucidates experimental observations, and enables quantitative testing of the origin and output of coordinated NSC behaviors long term. This in vivo to modeling combination offers unprecedented resolution to unravel NSC population rules and their impact.

The initial NSC activation event is a determinant checkpoint affecting NSC maintenance and output

Our study focuses on two related NSC decisions: activation and division. We used PCNA expression as the best account of NSC activation in fixed preparations. In contrast, we focused on cytokinesis to refine the temporal window of dynamic analyses, which also read the “activation to division” duration. The distribution rules of NSC division events at each time point in live imaging (Figure 4) are identical to those describing NSC activation in fixed samples (Figures 1 and 2). Furthermore, by tracking a total of 1,203 lineages, the large majority (80%) of activation events were followed by cell division (Figure S5), indicating that the two events are largely slaves to each other. Thus, our conclusions more generally apply to NSC recruitment via division. This decision accounts for 80% of fate choices in the adult zebrafish pallium under physiological conditions (Barbosa et al., 2015; Than-Trong et al., 2020) and is also a relevant determinant of long-term NSC maintenance (Urbán et al., 2019).

We exclusively considered de novo activation/division events from quiescence, disregarding the second or third division events of NSCs that rapidly divide repeatedly, for two reasons. First, rapid consecutive NSC divisions without intervening quiescence phases generate transiently clustered aNSCs (Lupperger et al., 2020), but these events are rare (14 tracks in a total of 117 dividing tracks followed, 12% of NSCs) (Figure S5). Second, the initial NSC activation decision conditions both neurogenesis and the maintenance of NSC numbers. In both zebrafish and mice, NSC fates at division are unbalanced, with a bias toward NSC amplification (Rothenaigner et al., 2011; Than-Trong et al., 2020) or neurogenic fate and loss (Calzolari et al., 2015; Encinas et al., 2011; Fuentealba et al., 2012; Pilz et al., 2018). Thus, NSC activation indirectly affects the quantitative distribution of fates. Our findings therefore also provide insight into the processes that balance the maintenance and output of adult NSC niches over time.

Lineage-derived inhibitory feedbacks generate an “intrinsic niche” for NSC coordination

The spatiotemporal distribution of NSC activation events appears controlled by cell-cell interactions operating between progenitors, putting forward the concept of an intrinsic niche. This contrasts with situations in which SC properties depend on local extrinsic niches, as in the adult intestine, stomach, colon, or hair follicle: there, SC identity or fate is also flexible but spatially biased relative to local external cues such as geometry or non-progenitor cell types (Gehart and Clevers, 2019; Ritsma et al., 2014; Rompolas et al., 2012). In an intrinsic niche, SC population homeostasis is both the consequence and the origin of an internal systems dynamics. While the two principles are not mutually exclusive, an intrinsic niche is perhaps particularly suitable in the context of large SC populations that need to homogeneously generate progeny cells over extended distances, such as NSC niches or the interfollicular SC population in the adult mammalian skin (Belokhvostova et al., 2018; Blanpain and Fuchs, 2009). Interestingly, in the latter case, a recent study using intravital imaging showed that neighboring SCs coordinate their fate decisions to differentiate and divide (Mesa et al., 2018).

Major cellular actors of the pallial intrinsic niche are aNPs and dividing NSCs (MCs). It remains to be precisely identified what is read as the effect of MCs: cytokinesis per se or associated changes of cell morphology, activation, or any other obligatory associated event such as lineage progression and the generation of aNPs. Our modeling results point to aNPs as important components of the regulation exerted by MCs. Encoding the inhibitory effect of aNPs in the model appears sufficient for MCs to affect future neighboring MCs with a temporal delay similar to that measured in vivo, and modifying the half-life of aNPs directly affects this delay. Thus, a biological interpretation of the delay-coordinating MC behavior may be lineage progression and aNP generation.

The lineage relationship existing between receiving (NSCs) and signaling cells (MCs and aNPs) indicates that one coordination rule of the intrinsic niche is akin to a retroactive control. Such a process, gated via its own output, was theoretically modeled to instruct balanced cell fate choices within homeostatic cell populations (Lander et al., 2009), although without a spatial component. Different regulatory steps (self-renewal or division rate, in addition to SC activation rate) could be targets of the feedback (Lander et al., 2009). Here, an effect of aNPs on NSC self-renewal would not decrease the local number of aNSCs, but rather change cell fate post-division (i.e., affect NSC division mode). A feedback-increasing aNSC division rate, when modeled, was sub-optimal to predict the delayed MC effect (Figure S6B); importantly, such feedback is also at odds with the experimental data on Notch signaling effects. NSCs that activate under Notch blockade divide within 3 days (Alunni et al., 2013), while here, under physiological conditions, only ~50% of aNSCs have divided 3 days after entering the activated state (Figure S5G). Thus, if anything, Notch signaling decreases, rather than activates, the aNSC division rate in situ. In contrast, feedback from aNPs on qNSC activation rate (1) spatiotemporally captures the experimental data when encoded in the lattice model and (2) is in fitting with the quiescence-promoting role of Notch signaling in vivo (Alunni et al., 2013; Chapouton et al., 2010; Ehm et al., 2010; Engler et al., 2018; Imayoshi et al., 2010; Kawai et al., 2017). Thus, NSC activation is a major regulatory step in the spatiotemporal NSC coordination uncovered here. This step was also predicted to control NSC numbers in the aging mouse telencephalon (Kalamakis et al., 2019; Ziebell et al., 2018), although the feedback nature and spatial impact of this regulation remain to be studied.

The mechanism unraveled here is akin to lateral inhibition, well known in developmental systems, where it also frequently involves Notch signaling (Moore and Alexandre, 2020; Sjöqvist and Andersson, 2019). Previous work also described Delta-like 1 (DLL1)-mediated feedback from aNSCs and/or aNP equivalents in the SEZ (Ables et al., 2010; Kawaguchi et al., 2013), and we extend these findings by highlighting the spatiotemporal relevance of this mechanism in adult NSC niches. We also quantify its properties and dynamics and show its spatiotemporal impact on neurogenesis output. Only 64% of NSC divisions (asymmetric and neurogenic) lead to the production of aNPs (Than-Trong et al., 2020), and the majority of NSCs are not in contact with aNPs (Figures S5K–S5K’’). This is even more prominent in other pallial subdivisions, for example Dl (Figure S1B). Thus, in addition to being dependent on aNP regulation, the NSC activation rate likely also follows an overriding internal clock that accounts for NSC quiescence in the absence of an aNP neighbor. Dm likely meets a balance in which the combined NSC internal clock and aNPs effect become visible on a global scale on NSC activation events.

The adult pallial intrinsic niche permits the dynamic, self-sustained, and self-propagating coordination of NSC activation events in time and space

Our work identifies several of the fundamental systems properties of the adult pallium intrinsic niche, with respect to NSC activation control.

First, the interactions coordinating NSC state are transient. This is due to the short half-life of signaling cells and to the labile state that they encode, quiescence. Our NSC lattice model shows that these interactions are sufficient to generate balanced dynamics and maintain systems equilibrium and spatiotemporal correlations over durations equivalent to a lifetime. The fact that the process never becomes fixed stands in contrast to a number of lateral inhibition-mediated processes during embryogenesis, where final cellular states are encoded (Brown and Groves, 2020; Schweisguth and Corson, 2019). In the case of adult SC ensembles, homeostasis must be maintained over a lifetime while accommodating lineage generation.

Second, these interactions operate with a temporal delay. This delay is likely due to lineage progression, but may additionally involve other mechanisms yet to be discovered. Typically, when a quiescence-promoting signal such as Notch3 signaling is abolished or when NSC activation is triggered for repair, NSCs do not activate immediately (Alunni et al., 2013; Baumgart et al., 2012; März et al., 2011). Physiologically, the duration or depth of G0 or the different checkpoints needed for activation may thus introduce a delayed output from the moment when an inhibitory signal (e.g., exerted by a neighboring MC) is released.

Third, the inhibitory interactions are exerted on neighbors, hence, they control the spatial distribution of cell states. This is a fundamental point, as in the zebrafish pallium the absence of extensive cell migration implies that NSC activity determines neuronal location (Furlan et al., 2017). The modeled coordination of NSC states via aNP-driven LI decreases neuronal clustering over a lifetime; this is important for pallial architecture, and presumably function. Likewise, SGZ neurons remain local, and NSC distribution within the SEZ biases neuronal identity (Fiorelli et al., 2015; Gonçalves et al., 2016; Obernier and Alvarez-Buylla, 2019).

In line with these properties, the NSC lattice model is unique. First, unlike mathematical models of embryonic lateral inhibition (Binshtok and Sprinzak, 2018), it captures the spatiotemporal properties of a dynamic homeostatic system rather than a fixed final pattern. Second, it describes a system in which cell morphology is coupled with cell state, a feature that is important for proper spatial organization. Thus, it provides a new set of tools allowing theoretical analyses particularly suited for spatiotemporally coordinated and dynamic SC populations.

Interactions between SCs are being identified as important components of SC fate in several systems, revealing other intrinsic niches. In the interfollicular epidermis of the adult mouse, SC differentiation and division events are spatiotemporally coupled (Mesa et al., 2018). Likewise, SC loss triggers neighboring SC division in the Drosophila gut (Liang et al., 2017; de Navascués et al., 2012). Together with adult vertebrate NSC niches, these systems illustrate a common principle in which SC states and spatial organization are maintained as stable on a local scale through spatiotemporal interactions that then gradually propagate through the whole germinal tissue. Such mechanisms may more generally define the principles of intrinsic niches in adult SC systems.

Limitations of study

The long-term impact of the inhibitory interactions controlling NSC activation, and the link between aNP- and MC-mediated inhibitions, are inferred from modeling. At present, the slow dynamics of NSC behavior in vivo and the pleiotropic effects of Notch preclude intravital imaging analyses over the necessary time frame and under conditions of Notch blockade. The large-scale effects of the observed local interactions also remain to be studied and understood.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Antibodies
Mouse monoclonal (IgG1) anti- ZO1	Thermo Fisher	Cat#33-9100, RRID: AB_2533147
Mouse monoclonal (IgG1) anti- SOX2	Abcam	Cat#ab171380, RRID: AB_2732072
Mouse monoclonal (IgG2a) anti-GS	Millipore	Cat# MAB302, RRID:AB_2110656
Rabbit anti-DsRed	Takara	Cat# 632496, RRID:AB_10013483
Mouse monoclonal (IgG1) anti-Zrf-1 (target antigen, zebrafish GFAP)	ZIRC	Cat#zrf-1; RRID: AB_10013806
Chicken anti-mCherry	EnCor Biotechnology	Cat# CPCA-mCherry, RRID:AB_2572308
Rat monoclonal anti-BrdU	Abcam	Cat#ab6326; RRID: AB_305426
Chicken anti-GFP Antibody	Aves lab	Cat#GFP-1020; RRID: AB_10000240
Rabbit Polyclonal anti-PCNA	GeneTex	Cat#GTX124496; RRID: AB_11161916
Mouse anti-PCNA IgG2a (PC10)	Santa Cruz Biotechnology	Cat# sc-56, RRID:AB_628110)
Goat anti-Mouse IgG2a Alexa633 conjugated	Thermo Fisher Scientific	Cat# A-21136, RRID:AB_2535775
Goat anti-Mouse IgG1 Alexa546 conjugated	Thermo Fisher Scientific	Cat# A-21123, RRID:AB_141592)
Goat Anti-Chicken IgG(H+L) Alexa488 Conjugated	Thermo Fisher Scientific	Cat# A-11039, RRID:AB_142924
Goat Anti-Rabbit IgG(H+L) Alexa405 Conjugated	Thermo Fisher Scientific	Cat# A-31556, RRID:AB_221605
Goat anti-Rat IgG-488 IgG(H+L) Alexa488 Conjugated	Thermo Fisher Scientific	Cat#A-11006, RRID:AB_2534074
Chemicals, peptides, and recombinant proteins
LY-411575	Sigma-Aldrich	Cat#SML0506
5-Bromo-2-deoxyuridine (BrdU)	Sigma-Aldrich	Cat#B5002
Antigen Retrieval (HistoVT One)	Nacalai Tesque	Cat#06380-05
4-hydroxytamoxifen	Sigma-Aldrich	Cat# T176
Experimental models: Organisms/strains
Zebrafish: AB WT strain	N/A	ZFIN: ZDB-GENO-960809-7
Zebrafish: Tg(gfap:GFP)mi2001	Zebrafish International ResourceCenter, Eugene, OR	ZDB-TGCONSTRCT-070117-154
Zebrafish Tg(mcm5:EGFP)	Zebrafish International ResourceCenter, Eugene, OR	ZFIN ID: ZDB-TGCONSTRCT-160126-1
Casper (roy−/−;nacre−/−) (mitfaw2/w2; mpv17a9/a9)	Zebrafish International ResourceCenter, Eugene, OR	ZDB-FISH-150901-6638
Zebrafish Tg(deltaA:GFP)	Zebrafish International ResourceCenter, Eugene, OR	ZFIN ID: ZDB-TGCONSTRCT-100823-1
Software and algorithms
Black Zen software	Carl Zeiss	RRID:SCR_018163
Imaris	Bitplane	http://www.imaris.oxinst.com/packages, RRID: SCR_007370
Fiji	Fiji	https://fiji.sc, RRID: SCR_002285
MATLAB 2017a	MATLAB	MATLAB, RRID:SCR_001622
R Project for Statistical Computing	R Project for Statistical Computing	http://www.r-project.org/, RRID:SCR_001905
Prism 8	GraphPad	https://www.graphpad.com/, RRID:SCR_002798
Illustrator CS6	Adobe	Adobe Illustrator, RRID:SCR_010279

Resource availability

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, Laure Bally-Cuif (laure.bally-cuif@pasteur.fr).

Materials availability

This study did not generate any unique reagents.

Data and code availability

Raw data on cell positioning used for the spatial statistics are available at: https://github.com/fcheysson/zebrafish-project Codes to generate simulations with the NSC lattice model and curve fitting for ${\gamma }_a$ estimation are available at: https://github.com/Udi-Binshtok/NSC_Lattice_model_2020

Experimental model and subject details

Fish husbandry and lines

All animal experiments were carried out in accordance to the official regulatory standards of the department of Essonne (agreement number A 91-577 to L.B.-C.) and department of Paris (agreement number A 75-1522 to L.B.-C. and N.D.) and conformed to French and European ethical and animal welfare directives (project authorization from the Ministère de l’Enseignement Supérieur, de la Recherche et de l’Innovation to L.B.-C.). Zebrafish were kept in 3.5-l tanks at a maximal density of five per litter, in 28.5°C and pH 7.4 water. Three- to four-month-old adult zebrafish were used; Tg(gfap:eGFP) (Bernardos and Raymond, 2006), Tg(gfap:dTomato) (Satou et al., 2012), Tg(mcm5:eGFP)^gy2 (Dray et al., 2015) and Tg(deltaA:GFP) (Madelaine and Blader, 2011). For live imaging Tg(gfap:dTomato)/+;Tg(mcm5:eGFP)^gy2/+ in the casper double mutant background (roy^−/−;nacre^−/−) (White et al., 2008) were used. The Tg(her4:VenusPEST) line was obtained by injecting 1 nL of a mix containing the her4:VenusPEST plasmid at 60 ng/μl together with 40 ng/μl transposase capped RNA into 1-cell stage AB embryos. F0 adults were then screened for fluorescence transmission in order to generate a stable line. The her4:VenusPEST construct was obtained using the multisite Gateway technology (Fisher Scientific) and the Tol2kit system (Kwan et al., 2007). This construct is designed to express a destabilized Venus protein using the Notch protein PEST domain fused to Venus (Ninov et al., 2012). A PCR fragment encoding the N-terminal of the zebrafish Her4 protein (first exon of 19 aa, first intron and 11 aa of the second exon) was fused to the construct encoding VenusPEST with the Phusion polymerase (Fisher Scientific) and the NEBuilder® HiFi DNA Assembly Cloning Kit (NEB). This insert was PCR amplifidr (forward primer KpnI-her4: gatcGGTACCatgactcctacaatcactggatc, reverse primer SacII-VenusPEST: atcCCGCGGctacacattgatcctagcagaag) then inserted into pME-MCS (Tol2kit #237) and recombined with p5E-her4 (Furlan et al., 2017) and p3E-polyA (Tol2kit # 302) in pDestTol2CG2 (Tol2kit #395).

Method details

BrdU pulse labeling

BrdU was applied in the fish swimming water for 6h at a final concentration of 1 mM for BrdU. After the pulse, fish were transferred to a tank with fresh fish water during chase period of 2 to 24h.

LY411575 treatment

Stock solutions of LY411575 (LY) at 10 mM were prepared by disolving 5 mg of LY in 1.05 mL DMSO and stored at −80°C until use. To block Notch signaling, LY was applied in the fish swimming water at a final concentration of 10 mM (Alunni et al., 2013). The solution was refreshed every 24 h. Control fish were treated with the same final concentration (0.1%) of DMSO carrier.

Clonal analysis of aNP migration

We used the same fish as produced in Than-Trong et al. (2020). Briefly, 3mpf Tg(her4.1:ERT2CreERT2);Tg(ubi:switch) double transgenic fish were immersed for ten minutes in fish water containing 0.5 μM 4-hydroxytamoxifen (4-OHT - Sigma-Aldrich, T176), then rinsed at least 3 times with fresh water over 48 hours before being chased. Clones were analyzed by whole-mount immunohistochemistry against mCherry, and the analysis here was restricted to clones containing a single NSC and one or several NPs. Nearest-neighbor distances (NNDs) between the NSC and NPs were extracted with Imaris and MATLAB. When several NPs were present in a clone, NNDs were first averaged. NNDs were then normalized by the average cell size for each brain in order to provide an estimation of NNDs in cell diameters. Box and whisker plots display the mean, median, first and third quartiles as well as the minimum and the maximum of NNDs for the analyzed brains.

Whole-mount immunohistochemistry

Brains were dissected in PBS, transferred to a 4% paraformaldehyde solution in PBS for fixation (2 hours at room temperature or overnight at 4°C) dehydrated and kept in 100% methanol at −20°C.

Brains stored in 100% MeOH were rehydrated and washed 3 times with PBST (0.1% Tween-20 in PBS).

For BrdU an antigen retrieval step was performed with an incubation in 2 M HCl (Sigma-Aldrich, 258148) at room temperature for 30 min. For proliferating cell nuclear antigen (PCNA) immunolabeling, an antigen retrieval step was performed with an incubation in HistoVT One (Nacalai Tesque) for an hour at 65°C. Brains were then washed three times for 5 min each with PBST, incubated into Blocking Solution (5% Normal Goat Serum, 0.1% DMSO, 0.1% Triton X-100 in PBS) (Sigma Life Science, 1002135493) for 1 h at RT. Primary antibodies were diluted in blocking Solution and incubated for 24 h at 4°C. The following primary antibodies were used: anti-ZO1 (Mouse, 1:200, Thermo Fisher Scientific), anti-SOX2 (Mouse, 1:200, Abcam), anti-GFAP (zrf1), anti-GS (Mouse, 1:1000, Millipore), anti-mCherry (Chicken, 1:1000, EnCor Biotechnology), anti-Zrf1 (mouse, 1:500, ZIRC), anti-DsRed (Rabbit, 1:250, Takara), anti-GFP (Chicken, 1:500, Aves Labs), anti-BrdU (Rat, 1:150, Abcam), anti-PCNA (Rabbit, 1:500, GeneTex), anti-PCNA (Mouse, 1:500, Santa Cruz Biotechnology). Brains were subsequently washed six times for 15 min with PBST and incubated for 24h at 4°C with secondary antibodies diluted 1:1000 in Blocking Solution.

The following secondary antibodies were used: anti-IgG2a conjugated to Alexa633 (Thermo Fisher Scientific), anti-IgG1 conjugated to Alexa546 (Thermo Fisher Scientific), anti-Chicken IgG(H+L) conjugated to Alexa488 (Thermo Fisher Scientific), anti-Rabbit IgG(H+L) conjugated to Alexa405 (Thermo Fisher Scientific), anti-Rat IgG conjugated to Alexa488 (Thermo Fisher Scientific). Brains were then washed six times for 15 min with PBST.

Confocal imaging whole-mounted immunohistochemistry

Fluorescent images of whole-mount telencephali were acquired on confocal microscopes (LSM700 and LSM710, Zeiss), using a 40X oil objective (Plan-Apochromat 40x/1.3 Oil M27) with an optical sectioning in Z every 0.5 μm and a tile scan of 4 to 8 Z stacks. Stitching was done with the ZEN software after imaging.

Fish anesthesia and mounting for intravital imaging

Anesthesia and mounting for imaging were conducted as in previous studies (Dray et al., 2015; Than-Trong et al., 2020). Briefly, anesthesia was initiated by soaking the fish for approximatively 90 s in water containing 0.01% MS222 (Sigma-Aldrich). They were then transferred into a water solution of 0.005% (v/v) MS222 and 0.005% (v/v) isoflurane to maintain the anesthesia during the whole duration of the imaging session and mounted in a home-made plastic dish between pieces of sponge. Overall, fish were anesthetized for about 30 min per session.

Multiphoton intravital imaging and analysis

The intravital imaging was performed on a customized commercial multiphoton microscope (TriM Scope II, LaVision BioTec) equipped with an ultrafast oscillator (λ = 690 to 1300 nm; InSight DS+ from Spectra-Physics Newport) and a MaiTai laser (TI:Sapphire, λ = 690–1040 nm Spectra-Physics). dTomato was excited at 1120 nm and GFP at 950nm. The fluorescent signal was collected with GaAsP detector (H7422-40, Hamamatsu). To image the entire volume of interest, spanning typically 800 μm by 800 μm by 250 μm (i.e., a single brain hemisphere), we recorded mosaics consisting of four z stacks with an overlap of 10%. For each z stack, the lateral field of view was 405 μm by 405 μm, the depth of imaging varied from 250 to 290 μm (starting about 250 μm below the skin), the voxel size was 0.8 μm by 0.8 μm by 2 μm, and the pixel dwell time was 4.9 μs.

Quantification and statistical analysis

Image analysis of immunohistochemistry

3D renderings were generated using the Imaris® software (versions 8 and 9, Bitplane). The 3D image was cropped to feature only the pallium as our region of interest and histograms was adjusted for each channel. The images were segmented manually using semi-automatic detection with the Imaris spots function followed by manual curation in the dorsomedial part (Dm) of the pallium (Dray et al., 2015; Than-Trong et al., 2020). Except for the BrdU experiment, at least 3 brains were analyzed per condition (WT, LY, DMSO), n represent the number of brains analyzed (one hemisphere per brain with 700 to 1919 cells counted per hemisphere), SEM and SD are presented. For the BrdU experiment 2 fish were analyzed and n represents the total number of cells. Mean cell diameters (r = 1) are the mean distances between qNSCs, aNSCs and aNPs (Figures 1E and 1F: 9.92 μm; Figure 2E: LY: 11.21 μm, DMSO: 9.71 μm; Figure S2: mean 10.07 μm, SD 0.35 μm; Figure S4: mean LY: 11.02 μm, SD 0.30 μm, mean DMSO: 11.06 μm, SD 1.2 μm), qNSCs and aNSCs or qNSCs, aNSCs and MCs (Figures 4 and 5, respectively) (Bibi: 12.88 μm, Mimi: 13.19 μm, Titi: 13.79 μm), measured with the Imaris® software. In all spatial analyses of simulations, mean cell diameters (r = 1) are mean distances between qNSCs, aNSCs and aNPs (Figures 6E,” 6E’’’, and 7B: average cell diameter over all the simulations and time-steps, 10 μm; Figures 7C and 7D: we converted the simulated units into microns by comparing the average cell diameter from the simulation to the one from the experiments [10 μm for the x-y plane, see Figure S2] and by using the experimental stacking rate of neurons (this is 30 μm over 2 months for the z axis)(Than-Trong et al., 2020).

Statistical analyses (except the spatial statistics) were carried out using Prism and Microsoft Excel. All the statistical tests performed were two-tailed, and their significance level was set at 5%.

Image analysis of intravital imaging

Image were combined and analyzed as in previous studies (Dray et al., 2015). Briefly, Z stacks acquired on successive imaging were first converted into a single file after cropping two files in the three dimensions using Imaris® (Bitplane) or Fiji. The alignment was done at the cellular level using landmark-based registration for which a few cells are detected and manually tracked over time and their average drift was corrected using Imaris. The histograms of fluorescence intensity were adjusted ‘by eye’ (linear stretch of the histograms) to correct the minor fluctuations in intensity from one day to another. After alignment, all cells were manually detected using Imaris® and their position where exported for further analysis via MATLAB®. Three fish were analyzed (mimi, titi and bibi), n represent the number of brains analyzed (one hemisphere per brain) with 300 to 500 cells tracked over eight time points every 3 to 4 days over 23 days total (one to two more time points were acquired after these 23 days but not analyzed because the interval between time points was longer). Statistical analyses (except the spatial statistics) were carried out using Prism and Microsoft Excel.

Spatial statistics (point pattern analysis)

Summary statistics

To determine whether there exists an interaction between two specific states of cells $i$ and $j$ ($i,j=$ aNSC or aNP), we analyze their relative positions using three multitype second-order summary statistics (Figure S3):

• •Besag’s $L$-function (Besag, 1977) is a variance-stabilized version of Ripley’s $K$-function (Ripley, 1977) which averages the number of cells of state $j$ within a distance $r$ of a typical cell of state $i$. It is a popular technique for analyzing spatial correlation in point patterns, usually by visually inspecting the empirical $\hat{L}$-function, calculated from the data, and comparing it to the theoretical $L$-function of the homogeneous Poisson process $L_{pois}\left(r\right)=r$, which serves as a benchmark for ‘no correlation’: for example, if $\hat{L}\left(r\right)<L_{pois}\left(r\right)$, this indicates that there are fewer neighbors than would be expected for a completely random pattern, consistent with some type of inhibition or repulsion between cells. While the $L$-function is good at detecting spatial correlation, it is not adapted to measure the range of said interaction, as it is of cumulative nature: for example, with patterns exhibiting inhibition at small spatial scales, the cumulative effect could still be visible at larger spatial scales.
• •The pair correlation function $g$ counts contributions from cells of state $j$ at a distance equal to $r$ of a typical cell of state $i$: it is the derivative of the $K$-function, rescaled such that, for a typical random process, $g_{pois}\left(r\right)=1$. As a complementary tool to the $L$-function, the $g$-function helps detect the range of interaction between cells: an empirical value $\hat{g}\left(r\right)\ne 1$ suggests that there is a spatial correlation between cells distant of $r$.

Both the $L$- and $g$-functions must be corrected for edge effects to avoid the bias that occurs when counting the number of neighbors for cells close to the border of the observed area. In this paper, we use an isotropic correction to account for edge effects. Details on the theoretical properties, statistical estimation, computation and edge corrections of the $L$- and $g$-functions be found in Baddeley et al. (2016).

• •The $M$-function has been introduced recently in Marcon and Puech (2010) and Marcon et al. (2012), as an extension of the $K$-function. It is of cumulative nature and measures the frequency of cells ot state $j$ within a distance $r$ of cells of state $i$, relative to that over the whole observed area. One of its advantages is that it is easily interpreted: for example, $\hat{M}\left(r\right)=2$ would indicate that the relative density is double that in the observed area.

Hypothesis testing and simulation envelopes

To assess whether the interaction between cells of states $i$ and $j$ is statistically significant, we perform Monte Carlo tests based on simulation envelopes of the summary functions. These envelopes are constructed by generating simulated patterns and their summary statistics from the “random labelling” null hypothesis ${\mathcal{H}}_0$, which assumes that the state of any cell is random with fixed probabilities and independent of other cells’ positions. The simulated patterns are generated by randomly permuting cells of state $j$ among all cells while keeping those of state $i$ fixed. The simulation envelopes provide acceptance intervals (or non-rejection intervals) for the null hypothesis: if the empirical function lies outside the simulation envelopes, then ${\mathcal{H}}_0$ may be rejected at a significance level that is inversely proportional to the number of patterns simulated (Figure S2A). Note that ${\mathcal{H}}_0$ is different from the usual “complete spatial randomness and independence” null hypothesis, that assumes that the underlying processes for cells of state $i$ and $j$ are independent Poisson patterns, which is not a good model for cell patterns, as cells are subject to the hardcore constraint (no two cells can be too close to each other). In particular, the aforementioned empirical summary functions should not be compared to the theoretical value for the Poisson pattern.

We consider two types of envelopes, depending on whether the interaction is tested at a specific distance $r$ or over a range $[0,R]$ of distances:

• •Simultaneous envelopes are constructed by measuring, for each simulated pattern, the most extreme deviation between the empirical and expected values of the summary statistic, where the maximum deviation is taken over the range $[0,R]$. They correspond to a global test of spatial correlation, indicating that an interaction exists for cells within a distance $R$ if the observed curve ever lies, at any distance $r<R$, outside the simulation envelopes. We consider simultaneous envelopes for the $L$-function only, as it is the only function considered that has a stable variance with respect to $r$.

A second strategy for detecting spatial correlation with the $L$-function is the Diggle-Cressie-Loosmore-Ford (DCLF) test, as proposed by Cressie (1991), Diggle (1986), and Loosmore and Ford (2006). Instead of the most extreme deviation, the test uses the integrated squared deviation between the empirical and expected values of the summary statistic over the range $[0,R]$. It is complementary to the maximum deviation envelopes to detect spatial interaction between cells.

• •Pointwise envelopes are constructed by measuring, for each simulated pattern and each distance $r$, the most extreme deviation between the empirical and expected values of the summary statistic. Their interpretation requires the distance $r$ to be set in advance of the analysis. We consider pointwise envelopes for the $g$-function only, as a way to detect the range of spatial interaction if it exists (i.e., if the global test on the $L$-function has rejected ${\mathcal{H}}_0$). Ranges considered are $r=\mathrm{1,2}$ and $3$ average cell diameters.

Details on hypothesis tests and simulation envelopes for point patterns can be found in Baddeley et al. (2016).

Statistical approach

In view of the preceding methods, we consider the following statistical approach for the analysis of interaction between cells of states $i$ and $j$ on a homogeneous part of the brain (the Dm domain): (i) first, we consider global tests (both maximum deviation and DCLF) for the $L$-function: this indicates whether an interaction exists (Figures 1E and 2E); (ii) then, if an interaction exists, we consider pointwise tests for the $g$-function at distances $r=\mathrm{1,2}$ and $3$ average cell diameters: this indicates the exact range of the interaction (Figure 1F); (iii) finally, we measure the strength of the interaction with the $M$-function (Figure 1F). The mean cell diameter was estimated by calculating the mean area of a cell in the pattern, and assuming it had a circular area.

In order to determine whether the interaction between aNP and aNSC cells exists beyond the first-order neighbors (those cells that share a membrane), we calculate the distance between a typical aNP cell and its furthest first-order neighbor (which, for aNP cells, is in average the fourth nearest neighbor, since they have four direct neighboring cells). aNP cells too close to edges were excluded from this calculation, to avoid evident bias. We then report the ninety-fifth ${\hat{q}}_{0.95}$ centiles for this distance on the graph of the $g$-function (vertical green line) (Figure 1F). If the empirical $\hat{g}$-function does not lie outside the pointwise envelopes beyond this range, then it is unlikely that the interaction goes beyond direct neighboring cells.

Dynamic patterns

To determine whether some inhibition also occurs between division events, we consider the patterns at time steps t and t+Δt and note state i the mother cells of the former pattern and j those of the latter. In order to include the whole observation period, the L-, g- and M-functions for each pair of patterns t and t+Δt (t = 1,…,T-Δt) are pooled using a weighted average (Baddeley et al., 2016). Then, the same statistical approach as above can be employed to determine whether an interaction exists between mother cells (Figures 5 and 7).

Note that one-sided rather than two-sided statistical tests are used, assessing only whether dispersion between division events exists, but not clustering, as this analysis was motivated by the previous which found a statistically significant dispersion exerted by aNPs on aNSCs. Consequently, simulation envelopes are one-sided, and the DCLF test only considers the negative part of the deviation, i.e., only focuses on the ranges where the empirical summary function is below the expected one.

Some inhomogeneity in the density of cells of dynamic patterns was present due to the curvature of the germinal layer, manifesting as a gradient along the length of the live samples. To account for this inhomogeneity, the position of cells along this dimension was first rescaled according to a smoothing estimate of the density, before running the aforementioned spatial analysis.

Finally, to combine the results from the three fish, we use Fisher’s method (Fisher, 1954; Mosteller and Fisher, 1948) to pool the p-values $p_i$ from each hypothesis test into one test statistic:

$$X_{2k}^2=-2\sum _{i=1}^k\text{ln}\left(p_i\right).$$

Under the null hypothesis, these p-values follow a uniform distribution on the interval $\left[\mathrm{0,1}\right]$, and hence $X_{2k}^2$ follows a chi-square distribution with $2k$ degrees of freedom (Figures 5 and 7).

Analysis of simulations from the NSC lattice model

To ascertain whether the model correctly mimics the live patterns, we performed a similar spatial analysis of the model simulations, with and without LI. For the comparison of NSCs, summary functions were computed on days 300, 333, 367, 400, 433, 467, and 500, then pooled for each simulation (Figure 6). For the comparison of MCs, since in live patterns time steps were observed three days apart, with MCs in a time step corresponding to all the division events since the previous time step, the analysis of the model simulations was similarly set up: the MCs in every three consecutive days were grouped into one pattern, then each pair of these patterns t and t+Δt was analyzed then pooled in the same way as live patterns. Finally, for any given Δt, the results from the simulations were combined using Fisher’s method to pool their p values (Figure 7).

The comparisons between the situations under different modeling schemes (with versus without LI, with LI of different strength, with LI versus lateral induction and wild-type) of the interactions between aNSCs and aNPs at any time (Figures S6A”, S6B,” and S7C), between MCs (Figures 7B and S7D) and between neurons (Figures 7C and 7D) were carried out using permutation tests proposed by Hahn (2012), which consist in comparing the expected summary statistics for each situation. Formally, the test statistic is the integrated squared normalized difference between the expected L-functions with and without LI. The Monte-Carlo p value of the test is then evaluated by comparing the observed data with random permutations of the L-functions among the groups. Neurons were both analyzed in 3D (Figure 7C), and in 2D (Figure 7D) by projecting their positions to the plane parallel to the pallial surface. For the three-dimensional analysis of neurons, the summary function used is instead Ripley’s K-function, since the three-dimensional analog to the L-function is not variance-stabilized (Baddeley et al., 2016).

Justification of spatial statistics methods

The M-function: While the use of Ripley’s K-, Besag’s L- and pair correlation functions is widespread in spatial statistics, the development of the M-function is relatively recent, and its use has almost exclusively been circumscribed to economic applications, with only few applications to biology (Fernandez-Gonzalez et al., 2005). However, it presents some improvements to existing measures, mainly that it is a relative, rather than a topographic, measure of spatial concentration. As a consequence, measures of the M-function can be interpreted immediately as the relative density of points and give an estimate of the interaction strength exerted by NSCs.

Nevertheless, the L- and g-functions must not be discarded, as they are complimentary rather than rival to the M-function, and they have their advantages for hypothesis testing. First, the L-function has approximately stable variance with respect to the range $r$, which makes it a prime candidate for global tests based on simultaneous envelopes, which we used to determine whether an interaction was present. Second, the g-function was used to determine the range of the correlation, though other non-cumulative measures (the Kd-function (Duranton and Overman, 2005) or the m-function (Lang et al., 2019)) could have been used as well. Overall, the measures we used highlight the large statistical toolbox available to the study of spatial patterns in biology.

Multiple testing: Care must be taken when interpreting p-values resulting from the spatio-temporal analysis of division events (Figure 7). Since testing for each $\text{Δ}t$ time intervals is done on the same samples, the threshold for significance should be adjusted to account for multiple tests and avoid too many false positives. The most common approach is the Bonferroni correction, which adjusts the threshold by dividing it by the number of tests done. Five $\text{Δ}t$ time intervals were considered, so the Bonferroni-adjusted threshold for significance was 0.01 for a desired overall significance level of 0.05. This led, when testing the experimental samples, to the null hypothesis for $\text{Δ}t4$, i.e., non-correlation between division events, not being rejected in spite of the low p-value (0.026).

However, testing of 18 simulations from the NSC lattice model in the presence of aNP-driven LI reveals that the correlation is statistically significant at $\text{Δ}t4$ time interval, even at this adjusted threshold (p-value = 0.009) (Figure 7). Since there was no specific behavior in the model accounting for temporal delay between division events, this behavior must stem from the locally spatial aNP-driven LI. Indeed, the same test applied to 18 simulations in the absence of LI did not recover the interaction at $\text{Δ}t4$ time interval (p-value = 0.256) (not shown).

Finally, note the difference between Bonferroni correction and Fisher’s method. The former is used in the case of repeated tests on the same samples to avoid too many false positives, while the latter is adapted for replications of the same test on independent samples, to increase the statistical power of the test. While the Bonferroni correction could also be used in the second case to account for repeated tests, it would instead slightly decrease the statistical power (Moran, 2003).

Statistical interpretation of the delayed MC-MC inhibition

The variability measured experimentally in the duration of the aNSC phase (Figure S5G), and the fact that not all activation-prone qNSCs will be neighbored by an aNP (Figures S5K–S5K’’), suggests that the delay of the MC-MC interaction itself will be variable. The question in its detection is therefore also that of statistical power. The spatial analysis of 18 simulations showed that the delay was recovered at time interval $\text{Δ}t4$, while analysis of the simulations without LI did not find any statistical evidence for an interaction between division events (Figure 7). We further explored whether this delay appeared at interval $\text{Δ}t4$ or existed throughout the whole time period by analyzing another set of 16 simulations, for a total of 34 simulations. $p$-values obtained by pooling the results from these simulations show that the interaction is statistically significant at intervals $\text{Δ}t2$ through $\text{Δ}t5$, with a trend at $\text{Δ}t1$ (pooled p values at $\text{Δ}t1:$ 0.031, Δt2: 0.004, Δt3: 0.001, Δt4: 0.000, Δt5: 0.003). This is indicative of an interaction which would begin right after the division event, and persist through the whole time period, consistent with aNP-driven LI. That the interaction is only recovered at interval $\text{Δ}t4$ for small samples suggests that it is at this time interval that it is strongest, wherein statistical testing has more power.

Code reproducibility

We used R (R Development Core Team 2020) software, and packages spatstats (Baddeley and Turner, 2005) and dbmss (Marcon et al., 2015) to do the spatial and spatiotemporal analyses of NSCs, division events and neurons. The code and the datasets used in the publication are publicly available at https://github.com/fcheysson/zebrafish-project.

Generation of the NSC lattice model: mathematical approach

To gain insight into the dynamics of NSC activation, division, and differentiation, we developed a statistical spatiotemporal model of NSC behavior (workflow in Methods Figure S1). The model contains two layers: (i) A steady state mean field analysis of dynamic rate equations describing the transitions between the different progenitor cell states - qNSCs, aNSCs, aNPs, and differentiated neurons. The objective of this layer is to extract the dynamic parameters of the system that will be used in the second layer. (ii) The ‘NSC lattice model’ which contains stochastic simulations based on a 2D vertex modeling platform that simulate transition between cell states, cell divisions, and cellular differentiation in a disordered cell lattice (Figure 6B). The NSC lattice model captures two fundamental aspects of the system: (1) The stochastic nature of the processes and (2) the ability to capture spatial and spatiotemporal correlations.

Analytical model

In order to extract the system’s parameters, we first developed an analytical model that captures the NSC cell fate transitions (Figure 1C), with the experimentally observed cell fate proportions (Figures 1D and S1A”), transition rates (Figure S5G), and inhibition of qNSC activation by neighboring aNPs (Figures 1E and 1F). The possible transitions considered in the model are shown in Figure 6A.

Dynamic equations

The variables in our model correspond to the four different cell states:

$$q\equiv qNSCa\equiv aNSCp\equiv aNPP\equiv dividedaNP$$

We define ‘divided aNP’ as a different cell state since we have made a simplifying assumption that aNP can divide only once before differentiating into neurons, namely $p$ can divide to two$P$. This is based on the experimental observation that clusters of three or more aNPs are rare, compared to singlets or doublets (Figure S5J).

We also denote the transition rates and the differentiation probabilities following cell divisions in the following way:

$${\gamma }_{q\to a}=rat{e}_{qNSC\to aNSC}{\gamma }_{q\to N}=rat{e}_{qNSC\to Neuron}{\gamma }_a=rat{e}_{aNSC\to division}$$

$${\gamma }_{p\to N}=rat{e}_{aNP\to Neuron}{\gamma }_{p\to P}=rat{e}_{aNP\to division}$$

$${\gamma }_{P\to N}=rat{e}_{dividedaNP\to Neuron}$$

$$P_{qq}=ProbabilityforaNSCsymetricdivisioninto2qNSCs$$

$$P_{qp}=ProbabilityforaNSCasymmetricdivisioninto1qNSC+1aNP$$

$$P_{pp}=ProbabilityforaNSCsymmetricdivisioninto2aNPs$$

The differential equations corresponding to the 4 cell states are (Figure 6A):

$$\frac{dq}{dt}=\left(P_{qp}+2P_{qq}\right){\gamma }_{a}a-{\gamma }_{q\to a}I\left(q,p,P\right)q-{\gamma }_{q\to N}q$$ (Equation 1)

$$\frac{da}{dt}={\gamma }_{q\to a}I\left(q,p,P\right)q-{\gamma }_{a}a$$ (Equation 2)

$$\frac{dp}{dt}=\left(P_{qp}+2P_{pp}\right){\gamma }_{a}a-{\gamma }_{p\to N}p-{\gamma }_{p\to P}p$$ (Equation 3)

$$\frac{dP}{dt}=2{\gamma }_{p\to P}p-{\gamma }_{P\to N}P$$ (Equation 4)

Here, the lateral inhibition (LI) on qNSC transition rate into aNSC, by a neighbor aNP, is written as a multiplication between the parameter ${\gamma }_{q\to a}$ and a function$I\left(q,p,P\right)$ which depends on $q,p$ and $P$, and satisfies $I\in \left[\mathrm{0,1}\right]$. Depending on neighboring qNSC and aNP, $I=1$ in case a qNSC does not neighbor an aNP, otherwise$I<1$. Thus, ${\gamma }_{q\to a}$ is the rate for $qNSC\to aNSC$ in case a qNSC does not neighbor an aNP and therefore it is not inhibited. We note that our model does not consider a situation where aNSC transitions back to a qNSC state without dividing since these are rarely observed experimentally.

Steady-state and mean field analyses

It is understood that different qNSCs will have a different transition rate due to LI that depends on time and space (e.g., on the presence or absence of aNP neighboring cells). In the following steady state analysis we replace the many possible interactions between $qNSCs$ and $aNPs$ by an approximated mean value for $I$. Thus, at steady state, we get a roughly constant number of cells that are inhibited and therefore a constant average reduction factor denoted$I^{\star }$:

$$I^{\star }\approx constant$$ (Equation 5)

Accordingly,${\gamma }_{q\to a}{I}^{\star }$ is an effective average transition rate between qNSC and aNSC. For example, if on average half the qNSCs are completely inhibited from making a q- > a transition, then $I^{\star }=\left(1/2\right)$ and the effective average transition rate is $\left(1/2\right){\gamma }_{q\to a}$. Such approximation is known as a mean field approximation where in the above described system the LI effect is treated as an effective external field rather than multi-cell-to-cell interactions. We ultimately use this approximation, along with measured experimental values, to extract the dynamic parameters from the model.

At steady state, Equations 1, 2, 3, and 4 equal to zero and we get the following relations:

$$\left({\gamma }_{q\to a}{I}^{\star }+{\gamma }_{q\to N}\right)q=\left(P_{qp}+2P_{qq}\right){\gamma }_{a}a$$ (Equation 6)

$${\gamma }_{a}a={\gamma }_{q\to a}{I}^{\star }q$$ (Equation 7)

$$\left({\gamma }_{p\to N}+{\gamma }_{p\to P}\right)p=\left(P_{qp}+2P_{pp}\right){\gamma }_{a}a$$ (Equation 8)

$${\gamma }_{P\to N}P=2{\gamma }_{p\to P}p$$ (Equation 9)

Which leads to a condition for a steady state:

$$\frac{{\gamma }_{q\to N}}{{\gamma }_{q\to a}{I}^{\star }}=P_{qp}+2P_{qq}-1$$ (Equation 10)

From Equation 10 one can see that $qNSC$ direct differentiation rate is zero in the case where per unit time the amount of qNSCs that divides is equal to the amount of qNSCs that are produced from divisions (symmetric + asymmetric divisions).

Parameters extraction and evaluation from measured quantities

We define $f_q,f_a,f_p$ and $f_P$ as the fractions of the variables:

$$f_q=\frac{q}{q+a+p+P}{f}_a=\frac{a}{q+a+p+P}{f}_p=\frac{p}{q+a+p+P}{f}_P=\frac{P}{q+a+p+P}$$ (Equation 11)

From the fractions in Equation 11 we substitute the variables$q$, $p$ and $P$ with$a$, in order to get the following relations:

From Equation 7 we get

$${\gamma }_a{f}_a=I^{\star }{\gamma }_{q\to a}{f}_q$$ (Equation 12)

From Equations 8 and 9 we get

$${\gamma }_{p\to N}+{\gamma }_{p\to P}=\left(P_{qp}+2P_{pp}\right)\frac{f_a}{f_p}{\gamma }_a$$ (Equation 13)

$${\gamma }_{p\to P}=\frac{f_P}{2f_p}{\gamma }_{P\to N}$$ (Equation 14)

For simplicity we assume that the differentiation rates for aNP and divided aNP are the same. We denote:

$${\gamma }_{P\to N}={\gamma }_{p\to N}$$ (Equation 15)

From the relations in Equations 10, 12, 13, 14, and 15, the dynamic parameters are all given by${\gamma }_a$:

$${\gamma }_{q\to a}=\frac{1}{I^{\star }}\frac{f_a}{f_q}{\gamma }_a$$ (Equation 16)

$${\gamma }_{q\to N}=\left(P_{qp}+2P_{qq}-1\right)\frac{f_a}{f_q}{\gamma }_a$$ (Equation 17)

$${\gamma }_{p\to N}=\left(P_{qp}+2P_{pp}\right)\frac{2f_a}{2f_p+f_P}{\gamma }_a$$ (Equation 18)

$${\gamma }_{p\to P}=\left(P_{qp}+2P_{pp}\right)\frac{f_P}{f_p}\frac{f_a}{2f_p+f_P}{\gamma }_a$$ (Equation 19)

$${\gamma }_{P\to N}=\left(P_{qp}+2P_{pp}\right)\frac{2f_a}{2f_p+f_P}{\gamma }_a$$ (Equation 20)

We will next estimate the constants:${\gamma }_a$, $P_{qq}$, $P_{qp}$, $P_{pp}$, $f_q$, $f_a$, $f_p$, $f_P$, and$I^{\star }$.

Parameter estimation

Estimation of${\gamma }_a$: From the experimental live tracks (Figure S5A) we estimated the duration of the aNSC phase before division. For each fish (Titi, Mimi and Bibi) we counted the number of tracks in which the aNSC phase duration before division was between 0-2, 3-5, 6-8, 9-11, 12-14 and 16 or more days. We then estimated the number of tracks that has not divided by a specified time, t. We then fitted fractions of tracks that has not divided with a decaying exponent of the form$y=A{e}^{-{\gamma }_{a}t}$ (Figure S5G), where $A$ is set to $1$ (normalized), $t$ is the time in days, and $y$ is the average fraction of aNSCs tracks that has not divided by time t. Fitting was performed by non-linear least mean square fitting procedure, with $\left(1/ST{D}^2\right)$ as weights for each data point (at 0 and 16 days the weight was set to${10}^4$). The best fit for the aNSC decay rate is ${\gamma }_a=0.22da{y}^{-1}$ with 95% confidence interval of $\left(0.2,0.25\right)$. The code for the curve fitting is available in the github link provided below.

Estimation of probabilities and fractions: From the experimental part (Figures S5G–S5I), we use the following measured values:

$$P_{qq}=0.30P_{qp}=0.58P_{pp}=0.12$$

$$f_a=0.031f_p=0.059f_{p+P}=0.12where{f}_{p+P}=f_p+f_P$$

We can then calculate the remaining of the fractions (from the definition in Equation 11):

$$f_q=0.849f_P=0.061$$

Estimation of $I^{\star }$: To simplify the estimation of the mean reduction in qNSC transition rate we assume that if a qNSC is neighbor with one or more aNPs then it is completely inhibited (i.e., it has no chance at all to become aNSC while inhibited. See also alterntive assumptions in the LI section below). Under the complete inhibition assumption, the function $I\left(q,p,P\right)$ gets the form:

$$I\left(q,p,P\right)=\{\begin{array}{ll}0\hfill & ifqNSC\text{is in direct contact with an immediate neighbor }aNP\hfill \\ 1\hfill & otherwise\hfill \end{array}$$ (Equation 21)

Then, the estimation of $I^{\star }$ is the average fraction of qNSC that are not neighboring aNP and therefore are not inhibited. From cell detection of the DM static images from the 4 fish (Figure 1B) we were able to count the fraction of cells that have one or more aNP neighbors (Figures S5K–S5K’’). The fraction of qNSCs that do not neighbor aNP comes out $0.594\pm 0.084$ ($4fishaverage\pm STD)$. We therefore used the following value $I^{\star }=0.59$.

From Equations 16, 17, 18, 19, and 20, with the estimations and assumptions above, we obtain all the model parameters (Methods Figure S1A). These parameters are used in a computer simulation as described below.

Generation of the NSC lattice model: lattice construction

Stochastic simulations on a cell lattice

To test our model, we developed a stochastic simulation platform that simulates the NSC behavior in the DM over 500 days (Video S2). We used a 2D vertex model, similar to the ones defined in Chiou et al. (2012), Farhadifar et al. (2007), and Staple et al. (2010), to generate a dynamic disordered lattice with about 260 cells (Figure 6B). We used periodic boundary conditions to avoid edge effects. To compare the model to the experiments, statistical analysis was done over a set of simulations such that the total number of cells from the set is in the order of the total number of cells tested experimentally. Each computer simulation is performed in two levels:

• 1.Tracking cell states and carrying out transitions and events using a probabilistic progression method (Methods Figures S1A, right, and S1B).
• 2.Applying changes in morphology according to the events and cell state (Methods Figures S1C–S1E).

Lineage events and LI

The simulations progress with time by calculating the probability for each cell at a certain time step to go through an event in the next time step. The specific event will take place if its probability exceeds a random number generated from a continuous uniform distribution from 0 to 1. The possible cell states and events are as described in the model flowchart (Figure 6A and Methods Figure S1B). The probability for each event,$P_{event}$, to take place at the next time step is calculated using the cumulative distribution function (CDF) of an exponential distribution, with ${\text{λ}}_{event}$ (the rate for that event) as the distribution rate parameter and $t=1timestep$:

$$P_{event}=1-e^{-{\lambda }_{event}t}$$ (Equation 22)

The simulation time interval (i.e., 1 time step) is defined as$1day$, and the parameters are used accordingly with the same dimensions (Methods Figure S1A). Therefore, the probabilities for each event are:

$$P_{q\to a}=1-e^{-{\gamma }_{q\to a}}$$ (Equation 23)

$$P_{q\to N}=1-e^{-{\gamma }_{q\to N}}$$ (Equation 24)

$$P_{a\to div.}=1-e^{-{\gamma }_a}$$ (Equation 25)

$$P_{p\to N}=1-e^{-{\gamma }_{p\to N}}$$ (Equation 26)

$$P_{p\to div.}=1-e^{-{\gamma }_{p\to P}}$$ (Equation 27)

$$P_{P\to N}=1-e^{-{\gamma }_{P\to N}}$$ (Equation 28)

The LI of $qNSC\to aNSC$ by neighboring$aNP$ is introduced in the simulation by a modification in the probability of $qNSC\to aNSC$ event (Equation (23)) with a term similar to the model function $I\left(q,p,P\right)$, as seen in Equations 1 and 2:

$$P_{qNSC\to aNSC}=\left(1-e^{-{\gamma }_{q\to a}}\right)h\left(q,p,P\right)$$ (Equation 29)

Here $h\left(q,p,P\right)$ is a function of $q,p$ and $P$ that reduce the probability of $qNSC$ activation in case of LI. In general, $h$ can be a dynamic and continuous function that might depend non-linearly on local parameters (e.g., identity of neighboring cells) and global parameters (e.g., cell density). Consistent with the simplification of $I$ (Equation 21) we simplify $h$ to be a step function that is 0 if the $qNSC$ in question is in direct contact with an immediate neighbor $aNP$ or 1 otherwise (see also below a case where this assumption is relaxed):

$$h\left(q,p,P\right)=\{\begin{array}{ll}0\hfill & ifq\text{is in direct contact with an immediate neighbor }porP\hfill \\ 1\hfill & otherwise\hfill \end{array}$$ (Equation 30)

In addition to the model that considers LI, we also consider a model that does not include lateral inhibition. In order to be able to compare between the two models we have to adjust the value of $I^{\star }$ to compensate for the overall effect of lack of inhibition. Based on the estimation we set $I^{\star }=0.59$ for the model with LI, and $I^{\star }=1$ for the model without LI. This compensation makes sure the fractions of cells in the different states and the percentages following symmetric/asymmetric cell divisions or direct differentiation are the same in both models (Figures 6C and 6D). We note that without this compensation, a model where LI is simply removed ($h=1$, ${\gamma }_{q\to a}$ stays the same) results in an increase in the fractions of aNSCs and aNPs beyond those observed experimentally (not shown).

We note that for simplicity we assumed that the inhibition functions, $I$ and $h$ in Equations 21 and 30 are binary. Other assumptions on the inhibition function can be considered, for example, the effect of aNPs on neighboring qNSCs may not induce a complete inhibition (i.e., qNSC activation rate is reduced to a finite number rather than to zero). Simulations with incomplete reduction of qNSC transition rate (for example 70% and 90% reduction) result in weaker spatial correlation between aNSCs and aNPs and weaker spatiotemporal correlations between MCs Figure S10(Figure S7), yet the effect still exists.

Changes in morphology

There are three main morphology changes in the lattice model:

• 1.Cell division.
• 2.Cell delamination.
• 3.Minimization of mechanical energy where each cell state has its own preferred area.

Because there are many events of division and delamination at a single time step, a standard 2D vertex model (such as in Staple et al., 2010) have a weakness where too many bonds are lost in the process and cells end up having only two bonds (with zero area). The simulation is therefore optimized to reduce the number of bonds lost during cell division and cell delamination (and even sometimes add bonds). The following rules are imposed on the simulations:

Cell division

Cell division is done differently for different cell geometries (Methods Figure S1C):

• •If the cell consists of 4 bonds then a new bond is added from the middle of the cell’s longest bond to the middle of the opposing bond.
• •If the cell consists of 5 bonds then a new bond is add from the middle of the cell’s longest bond to the farthest vertex opposing it.
• •If the cell consists of 6 or more bonds then a new bond is added from a random vertex to a vertex which is clockwise far away from it by this formula:

$$\#bondsbetweenthe2chosenvertices=\#vertices/2$$

Cell delamination

Cell delamination is done in two steps (Methods Figure S1D):

• 1.If the number of bonds is higher than 4, a T1 transition (intercalation) is applied (Staple et al., 2010).
• 2.If the number of bonds is 4 the cell is delaminated from the lattice.

The delamination process attempts to remove the cell from the lattice with a minimum reduction in the number of bonds from neighboring cells. Furthermore, the algorithm chooses to reduce the number of bonds from the neighbor/s [of the delaminated cell] with the maximum number of bonds. If a cell is surrounded only by cells that each has 4 bonds, the simulation then stops (rarely happens).

Mechanical energy minimization

At each time step, as division, delamination and transitions events occur, the lattice relaxes into a new morphological state while minimizing its mechanical energy (Methods Figure S1E). The mechanical energy, $E$, of the 2D lattice at time step $t$ is given by Farhadifar et al. (2007):

$$E\left(t\right)=\alpha \sum _{i\in cells}{\left(A_i-{\hat{A}}_i\frac{\#cell{s}_0}{\#cells(t)}\right)}^2+\beta \sum _{i\in cells}{L}_i^2+\gamma \sum _{i\in bonds}{l}_i$$ (Equation 31)

Where $\alpha ,\beta$ and$\gamma$ are constant coefficients. The first and second summations over the cells are the contribution to energy given by the area,$A_i$ and perimeter,$L_i$, respectively. The term ${\hat{A}}_i$ is the preferred area for cell$i$. Note that for each cell state - qNSC, aNSC and aNP, there is a different preferred area${\hat{A}}_{qNSC}$, ${\hat{A}}_{aNSC}$ and${\hat{A}}_{aNP}$, respectively (Estimated from experimental data, not shown). The parameters’ values for the energy function are given in Methods Figure S1E. Our simulations are presented on a fixed size image (Figure 6B), yet the number of cells can vary over time. For that reason the preferred area of cell $i$ is scaled by the factor$(\#cell{s}_0/\#cells\left(t\right))$, where $\#cell{s}_0$ is the number of cells in the lattice at the initial time step and $\#cells\left(t\right)$ is the number of cells in the lattice at time step$t$. The third summation over the bonds is the energy given by the bond’s tension, associated with its length, $l_i$ (we assume no difference in properties between bonds).

The minimization of Equation 31 is done after each cell division and cell delamination and after all transitions in the current time step took place (for example, after all activation events occurred at the time step). Note that the way the energy is minimized is by rearranging all of the vertices in a position which is in the direction that favors the reduction in energy. In our simulation we can control two parameters: the amount of movement in the vertices position (resolution) and the number of iterations in each time the minimization runs. If the resolution is too low (the movement is too large) then the lattice suffers from distortions. If the resolution is high then many iterations are needed in order to make a significance change. Parameters were optimized for highest resolution given the running time constraints. The values of these parameters are available within the code (See Simulation code and parameters below).

Morphology change due to geometry corrections

We note that our simulation keeps the lattice of cells under the following two restrictions:

• 1.Any vertex should share 3 cells exactly (no more, no less). If there exist a situation where a vertex is shared more than 3 cells, then a bond is added to the lattice (with a new vertex as well) which makes sure the vertex has only 3 cells sharing it (Methods Figure S1F). The bond is added in the following way: one of the cells that share the vertex is chosen randomly (with preference to choose an aNSC or aNP). Then a new vertex is added on the connecting axis between the original vertex and the center of the chosen cell. A new bond is then constructed between the original vertex and the new vertex, while the cells that originally shared the original vertex are rearranged with respect to the new created bond.
• 2.Any cell should have at least 4 bonds. If there exist a situation where a cell has 3 bonds, then the algorithm works out to add a bond to this cell (Methods Figure S1G) without causing a different cell to reduce its number of bonds to 3. Note that the creation of 3 bonds cells is avoided during the simulation.

Lattice generation and initial conditions

The cell lattices were generated by starting from an initial 18 by 18 regular hexagonal lattice with periodic boundary conditions. Then, random T1 transitions are performed to break the symmetry of the lattice and small cells are removed from the lattice. For initial conditions we generated a disordered lattice of about 260 cells and set all of the cells to be qNSC, then randomly choose 3.5% of them to be aNSC and different 12% of them to be aNP (where aNPs do not neighbor aNSCs). Afterward we minimized the lattice mechanical energy in order for the lattice to relax into a morphology that fits better the cells’ state.

Alternative models

In addition to the model described above, we also tested two alternative models:

A model with higher aNP division and differentiation rates (Figures S6A–S6A’’’):

In order to test the effect of aNP half-life on the time delay of the spatiotemporal correlation between division events, we performed a set of simulations where we increased the aNP division and differentiation rate by a factor 4/3, while keeping all of the other dynamic parameters the same. This is done by changing the fractions $f_q$, $f_a$, $f_p$ and $f_P$ but keeping the same ratio for$\left(f_a/f_q\right)$ and$\left(f_P/f_p\right)$. The parameters used in this model, different from our default model in Methods Figure S1A, are:

$$f_q=0.875f_a=0.032f_p=0.046f_P=0.047$$

$${\gamma }_{p\to N}=0.082da{y}^{-1}{\gamma }_{p\to P}=0.042da{y}^{-1}{\gamma }_{P\to N}=0.082da{y}^{-1}$$

We predicted that multiplying the aNP division and differentiation rates by a factor of 4/3 will result in a delay time of $\text{Δ}t3=6to9days$ (instead of $\text{Δ}t4=9to12days$ as observed experimentally and as in our original model). We confirmed this prediction in our analysis (Figure S6A–S6A’’’).

A model where aNPs act on the division rate of neighbor aNSCs (Figure S6B–S6B’’’):

To test the effect of enhancing the aNSC division rate, ${\gamma }_a$, when an aNSC is in contact with aNP, we performed a set of simulations, similar to the stochastic simulations described above but with the following assumptions:

• (i)There is no lateral inhibition of aNPs on the qNSC activation rate, ${\gamma }_{q\to a}$ (equivalent to $h=1$ all the time; see Equation 30).
• (ii)If an aNSC is found in contact with an aNP then its probability to divide at the immediate next time step, i.e., after 1 day, is set at 100%. Otherwise, it divides with a probability that depends on the division rate (as described in Equation 25).

All of the parameters are set to be as in our original model as if it was a model without LI (Methods Figure S1A).

Simulation code and parameters

We used MATLAB software to run the simulations. The code generating the simulations, as well as the code and data for the curve fitting of ${\gamma }_a$ estimation, are given in:

• https://github.com/Udi-Binshtok/NSC_Lattice_model_2020.

All of the parameters that were used in the simulations are found in Methods Figures S1A and S1E, as well as in the alternative models section above. These parameters are easily adjustable in the computer simulation code file named defaultparams.m.

Published: April 5, 2021