Predicting COVID-19 incidence in French hospitals using human contact network analytics

Abstract

Background  COVID-19 was first detected in Wuhan, China, in 2019 and spread worldwide within a few weeks. The COVID-19 epidemic started to gain traction in France in March 2020. Subnational hospital admissions and deaths were then recorded daily and served as the main policy indicators. Concurrently, mobile phone positioning data have been curated to determine the frequency of users being colocalized within a given distance. Contrarily to individual tracking data, these can be a proxy for human contact networks between subnational administrative units.

Methods  Motivated by numerous studies correlating human mobility data and disease incidence, we developed predictive time series models of hospital incidence between July 2020 and April 2021. We added human contact network analytics, such as clustering coefficients, contact network strength, null links or curvature, as regressors.

Findings  We found that predictions can be improved substantially (by more than $50\%$) at both the national level and the subnational level for up to 2 weeks. Our subnational analysis also revealed the importance of spatial structure, as incidence in colocalized administrative units improved predictions. This original application of network analytics from colocalization data to epidemic spread opens new perspectives for epidemic forecasting and public health.

1. Introduction

The COVID-19 pandemic revealed the importance of identifying early predictors of epidemic dynamics. Indeed, for this infectious disease, hospital admission data are usually the most reliable indicator but suffer from a 2-week delay with the current state of the epidemic (Salje, Kiem, Lefrancq, Courtejoie, Bosetti, Paireau, Andronico, Hozé, Richet, Dubost, Strat, Lessler, Levy-Bruhl, Fontanet, Opatowski, Boelle, Cauchemez, 2020, Sofonea, Reyné, Elie, Djidjou-Demasse, Selinger, Michalakis, Alizon, 2021). Screening test results can provide closer monitoring but they often suffer from strong sampling biases.

Mobility data gathered daily by telephone providers and Internet services can help to understand epidemic spread, as shown early in the pandemic using individual mobility (Kraemer et al., 2020). More recently, it was observed that epidemic growth ratios and effective reproduction numbers correlated with human mobility (Badr, Du, Marshall, Dong, Squire, Gardner, 2020, Cazelles, Comiskey, Nguyen-Van-Yen, Champagne, Roche, 2021, Fan, Lee, Yang, Oztekin, Li, Mostafavi, 2021), whereas other studies have used mobility data as early predictors of disease incidence (Funk, Abbott, Atkins, Baguelin, Baillie, Birrell, Blake, Bosse, Burton, Carruthers, Davies, De Angelis, Dyson, Edmunds, Eggo, Ferguson, Gaythorpe, Gorsich, Guyver-Fletcher, Hellewell, Hill, Holmes, House, Jewell, Jit, Jombart, Joshi, Keeling, Kendall, Knock, Kucharski, Lythgoe, Meakin, Munday, Openshaw, Overton, Pagani, Pearson, Perez-Guzman, Pellis, Scarabel, Semple, Sherratt, Tang, Tildesley, Van Leeuwen, Whittles, 2020, Paireau, Andronico, Hozé, Layan, Crepey, Roumagnac, Lavielle, Boëlle, Cauchemez, Zebrowski, Rundle, Pei, Yaman, Yang, Carr, Sims, Doorley, Schluger, Quinn, Shaman, Branas, 2021). For instance, mobile phone location data provided by Google Mobility Trends were used to calibrate individual movements (Pullano et al., 2020). However, a limitation of such data is that they involve only individual movement but disease transmission requires at least two people. Here we use data from Facebook Inc. that inform us on colocation (or colocalization); that is, not just the position of a single individual but also possible interactions of individuals with respect to their administrative unit of residence (see ‘Materials and methods’ for details). Similar data were used to simulate metapopulation models and investigate the effect of interventions on the resulting network (Chang, Kahn, Li, Lee, Buckee, Chang, 2021a, Chang, Pierson, Koh, Gerardin, Redbird, Grusky, Leskovec, 2021b). However, to our knowledge, these data have not yet been used to predict key features of the epidemic, such as hospital admissions or deaths.

The body of literature for COVID-19 time series analyses linking epidemiological data to public health measures or environmental factors is already widespread, ranging from cross-correlation analysis to complex predictive machine learning tasks (Ayinde, Lukman, Rauf, Alabi, Okon, Ayinde, 2020, Ballı, 2021, Gecili, Ziady, Szczesniak, 2021, Kumar, Susan, 2020, Satrio, Darmawan, Nadia, Hanafiah, 2021, Shahid, Zameer, Muneeb, 2020, de Souza, da Cunha, dos Santos, Correia, da Silva, de Lima Filho, Albuquerque, Santos, 2020). Some methods, such as neural networks, provide powerful predictions, but the interpretation of the results is offset by the method’s convolutive nature. Here we choose a middle ground and a more straightforward approach by combining standard autoregressive integrated moving average (ARIMA) models with original regressors of human contact derived from colocation data.

2. Materials and methods

Facebook Inc. recorded the position of mobile app users who agreed to turn location tracking on. Every week, users were assigned resident administrative regions based on consistent overnight stays. Given two administrative regions (the ‘departments’) $A$ and $B$, we denote by $N_A\left(w\right)$ and $N_B\left(w\right)$ the number of users assigned to each department in week $w$. The colocation probability between $A$ and $B$ for week $w$ is calculated as follows. The week $w$ is partitioned into 5-minute time bins $t_1^w,\cdots ,t_{2016}^w$. We denote by $f_{AB}\left(t_i^w\right)$ the number of users assigned to $A$ and $B$ located in the same 600 m${}^2$ grid cell within time bin $t_i^w$ during week $w$. If the total number of colocation events for a given week $w$ is denoted by $f_{AB}^w={\sum }_i{f}_{AB}\left(t_i^w\right)$, the (symmetric) colocation probability between $A$ and $B$ for week $w$ is then defined by

$$p_{AB}\left(w\right)=\{\begin{array}{cc}\frac{f_{AB}^w}{2016N_A\left(w\right)N_B\left(w\right)2}\hfill & \text{if}A\ne B,\hfill \\ \frac{f_{AA}^w}{2016N_A\left(w\right)(N_A\left(w\right)-1)2}\hfill & \text{otherwise.}\hfill \end{array}$$

In other words, the colocation probability is the quotient of the number of colocated user pairs divided by the number of all possible user pairs during a week (with 2016 slots of 5 minutes per week). Importantly, the colocation probability cannot distinguish between events where the same pair of users are colocalized for all 2016 time bins during a week or where a user was colocalized at each time bin with a different user.

For continental France, department-level colocation probabilities were directly provided by Facebook Inc. via the Web portal https://dataforgood.fb.com, with a total of $d=94$ departments covered. Therefore, we constructed $94\times 94$ matrices that capture the weekly colocation probabilities between users depending on their department of residence. These can readily be used to construct weighted contact networks. We also investigated the coverage of Facebook users with an assigned department of residence among the French population from the 2019 census data provided by the French National Institute of Statistics and Economic Studies (Insee; https://www.insee.fr).

To summarize temporal changes in the resulting weighted contact networks between French departments, we calculated for each week three node-based graph descriptors (clustering, strength and null links) and one edge-based graph descriptor (curvature). The node-based descriptors were calculated by constructing undirected, weighted graphs from colocation data. For clustering, we used the local clustering coefficient (‘transitivity’ function in the R package igraph), which calculates for a given node all edge weights between the node neighbours relative to the maximum neighbourhood clique size. This clustering coefficient is 1 if the node is contained in a clique (i.e. the node and all its neighbours are connected to each other). The strength of a node is calculated by summing the edge weights incident on the node (‘strength’ function in igraph). The number of null links represents the number of incident edges with zero weight and is bounded from above by $d-1$. Curvature was calculated in the sense of discrete Ollivier–Ricci curvature Ollivier (2007) with a Python code freely available at https://github.com/saibalmars/GraphRicciCurvature. The Ollivier–Ricci curvature of an edge $\overline{xy}$ compares the distance between two nodes $x$ and $y$ with the optimal transport cost $\mathcal{W}$ between uniform measures on unit balls centred at $x$ and $y$:

$$\text{curvature}(x,y)=1-\frac{\mathcal{W}(B_1\left(x\right),B_1\left(y\right))}{d(x,y)}.$$

Numerical studies showed that edges with positive curvature tend to be part of a cluster, whereas edges with negative curvature tend to act as bridges between clusters (Jost, Liu, 2013, Ni, Lin, Gao, Gu, Saucan, 2015, Ni, Lin, Luo, Gao, 2019). Therefore, a decrease in curvature can be seen as an indicator for connectivity breakdown.

For comparison, we also incorporated Google Community Mobility Report data (www.google.com/covid19/mobility/), from which we obtained the daily change as a percentage with respect to a pre-pandemic baseline in visits to grocery stores, parks, workplaces, residential areas, transit stations and retail stores. We calculated cumulative weekly changes matching the dates of the weekly recorded colocation data. Since Google Community Mobility Reports were not available at the department level, we used these data only for national-level analyses.

We downloaded the positive testing rate (i.e. the ratio of positive tests to all tests) from https://ourworldindata.org. To remove reporting bias, we calculated the rolling average with a right-aligned 7-day window and calculated the weekly positive test rate matching the dates of the weekly recorded colocation data.

We downloaded daily minimum, maximum and average temperature data at department level provided by Open Data Réseaux Énergies via the Web portal https://www.data.gouv.fr ; see also Table 1 . The data were aggregated into weekly minimum, maximum and average temperature. For the same data, we also calculated quantiles for national analysis.

Table 1.

Regressor name, description and source

Name	Description	Source
Null links	Colocation graph	Facebook Inc.
Strength	Colocation graph	Facebook Inc.
Clustering	Colocation graph	Facebook Inc.
Curvature	Colocation graph	Facebook Inc.
Between-department colocation	Colocation data	Facebook Inc.
Incidence in colocation graph neighbourhood	Colocation and incidence data	Facebook Inc.
Within-department colocation	Colocation data	Facebook Inc.
Facebook coverage	Colocation and census data	Facebook Inc., Insee
Retail and recreation percentage change from the baseline	Average weekly change	Google Community Mobility Report
Grocery and pharmacy percentage change from the baseline	Average weekly change	Google Community Mobility Report
Parks percentage change from the baseline	Average weekly change	Google Community Mobility Report
Transit stations percentage change from the baseline	Average weekly change	Google Community Mobility Report
Workplaces percentage change from the baseline	Average weekly change	Google Community Mobility Report
Residential percentage change from the baseline	Average weekly change	Google Community Mobility Report
Temperature	Weekly temperature by department	Open Data Réseaux Énergies
Positive test rate	Average weekly positive test rate	Our World in Data

COVID-19 hospital data for France were downloaded from https://www.data.gouv.fr. The data comprised daily hospital admissions, ICU admissions and deaths in hospitals by department. To match the Facebook Inc. colocation data, we considered only departments in continental France spanning the period from 24 March 2020 to 30 March 2021. For the country-wide analysis, we summed the daily incidence in all departments and calculated right-aligned 7-day rolling averages to remove reporting bias. Finally, we calculated the cumulative weekly incidence matching the dates of the weekly recorded colocation data. The weekly incidence data were log-transformed before the time series analysis.

The time series analysis was performed with the R package forecast. For each week, we trained and tuned ARIMA models on historical data starting from 24 March 2020 and performed forecasting for 1-week and 2-week horizons. Model parsimony during tuning was determined by the Akaike information criterion. The first 4 weeks were used for training only, and we started prediction at the fifth week of our records. For any particular week, starting from June 2020, the prediction accuracy was evaluated in terms of the mean average error between incidence data and predictions for the following 2 weeks. More precisely, given log-transformed incidence data $y$ from week $t$, with exogenous regressors $x^i$, the regression model with ARIMA error (Hyndman and Khandakar, 2008) is defined by

$$\begin{array}{ccc}\hfill y_t& =& \sum _i{\beta }_i{x}_t^i+n_t,\hfill \\ \hfill n_t& =& \sum _{i=1}^p{\alpha }_i{n}_{t-i}+{ϵ}_k-\sum _i^q{\theta }_i{ϵ}_{t-i},\hfill \end{array}$$

where the regression error $n_t$ is an ARIMA error, $p$ is the order of the autoregressive part, $q$ is the order of the moving average part and ${ϵ}_k$ are Gaussian errors. Note that $y$ and $x$ can undergo differencing up to order $d$ to ensure stationarity.

We used exogenous regressors based on quantiles of network descriptors, Facebook Inc. colocation data, Google Community Mobility Reports and positive testing rates to tune parameters $p$, $d$ and $q$ and to train each model. We then compared the prediction results from models using regressor data with those using historical incidence data alone.

The predictive power of combinations of regressors was assessed following a stepwise method. For each week, we started using a single regressor and incremented the set of regressors as long as the mean average error of the prediction decreased, thereby yielding a linear combination of regressors with minimum prediction error per week.

For the department-level models, we also applied regression models with ARIMA error. Node-based regressors (e.g. node strength and null links) were based on the actual values, whereas the edge-based curvature regressors consisted of quantiles relative to the department of interest. In addition, for each department, we also used incidence data for hospital admissions and deaths in departments with the 10 strongest colocation links to the department of interest (denoted by incid$\_$1, incid$\_$2, etc.).

3. Results

3.1. Network descriptors

The analysis of network descriptors showed a highly dynamic range for the clustering coefficients in relation to the hospital incidence data and underlying non-pharmaceutical interventions (Fig. 1 ). For instance, in the midst of the first national lockdown in April 2020, the minimum clustering coefficient was 0.6, but by July 2020 it had returned almost to the maximum level (close to 1). The number of null links, which offers a more discrete measure of decreasing connections between departments, reached 72 out of 93 possible null links (77%) for several departments in April 2020. In contrast, several departments exhibited small changes in null links, suggesting that the mobility restrictions impacted the colocation probabilities unevenly across the country. The network strength more than tripled during the same period in the departments, reaching the strongest colocation probability; a high level which was maintained throughout October 2020, while hospitalization increased again in September. The curvature trends followed those of the network strength but were more sensitive to perturbations, for instance around 1 January 2021.

Fig. 1.

Disease incidence data and network metric quantiles in France, aggregated by week.

We also investigated spatial snapshots of the network descriptors before and during the second lockdown period at the beginning of November 2020. Figure 2 shows, for these 2 weeks, the 50 strongest colocation weights per week between two departments (red edges) and the number of null links in the departments involved at the end of these links. These results point to spatial clusters of departments which maintained high colocation weights between each other (e.g. in the Paris region or in Eastern France) while shutting down connections to many other departments.

Fig. 2.

Fifty strongest between-department colocation links and null links from those departments in France at weeks beginning 3 November 2020 (left panel) and 10 November 2020 (right panel). The thickness of the red edges corresponds to the colocation weights in terms of pre-pandemic quantiles, and the size of the black dots shows the number of missing links to other departments in the particular week.

Correlation plots (Fig. S1) across all recorded weeks indicated a strong positive correlation between network strength, curvature and Google Community Mobility Report data (retail stores, grocery stores, parks and transit stations), but negative correlations between these quantities and null links. Interestingly, within-department colocation was only weakly correlated with Google Community Mobility Report data, supporting the hypothesis that colocation data could yield signals qualitatively different from more classical individual movement data.

3.2. Predicting national-level hospital incidence

The time series analysis showed that predictions made using only incidence data from past time points led to an average mean error of 1632 hospitalizations per week and 238 deaths per week (regressor group ‘none’ in Fig. 3 ). Including a single exogenous regressor across all time points clearly reduced the prediction error by about $13\%$ for hospital admissions and by $50\%$ for hospital deaths (Fig. 3). Quantiles from Facebook Inc. colocation data, such as network strength, clustering or null links, were among regressors that reduced prediction errors most. Google Community Mobility Report data related to recreation and residential movement also greatly improved predictions regarding deaths but not hospital admissions. Positive testing rate appeared to improve predictions only with 2-week horizons. Finally, temperature did not belong to the best predictors for hospital admissions or deaths.

Fig. 3.

Top-five predictive models for new hospital deaths (top) and admissions (bottom). The models with the lowest mean average error using network analytics as regressors for 1-week (left) and 2-week (right) horizons are shown. The error made in the model without an exogenous variable is shown in all panels. The colour code refers to the group of regressors used.

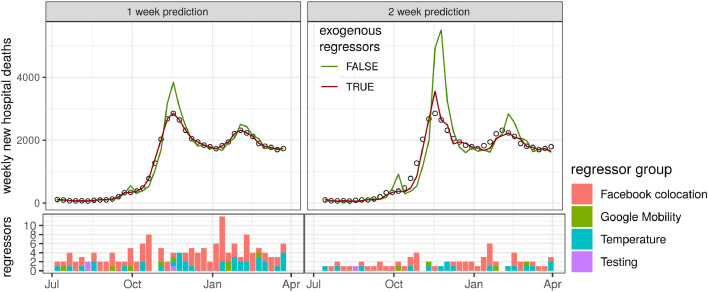
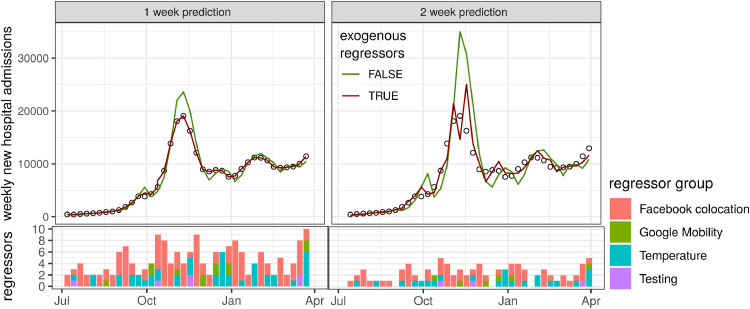
To further our understanding of temporal dynamics of hospital admissions, in particular at epidemic turning points, we determined for each week combinations of regressors that reduced the error the most. For the 1-week prediction horizon, we obtained almost perfect fits using regressor combinations mostly related to colocation networks (e.g. clustering and curvature quantiles) and, to a lesser extent, temperature (Fig. 4 ). Although combining regressors improved the model fit at the 2-week horizon compared with the model without exogenous regressors (the red curve), the model was not capable of reproducing the precision seen at the 1-week prediction horizon. Similarly, combining regressors to predict hospital deaths resulted in almost perfect fits for the 1-week horizon, and greatly improved fits for the 2-week horizon, albeit slightly overestimating peak deaths (Fig. 5 ).

Fig. 4.

Model fits to hospital admission incidence data (circles) with the lowest mean average error among all models using combinations of regressors (red line) compared with autoregressive models without exogenous regressors (green line). The bottom panels show the number of regressors used to obtain the best fits, colour-coded by the regressor group.

Fig. 5.

Model fits to hospital death incidence data (circles) with the lowest mean average error among all models using combinations of regressors (red line) compared with autoregressive models without exogenous regressors (green line). The bottom panels show the number of regressors used to obtain the best fits, colour-coded by the regressor group.

3.3. Predicting department-level hospital incidence

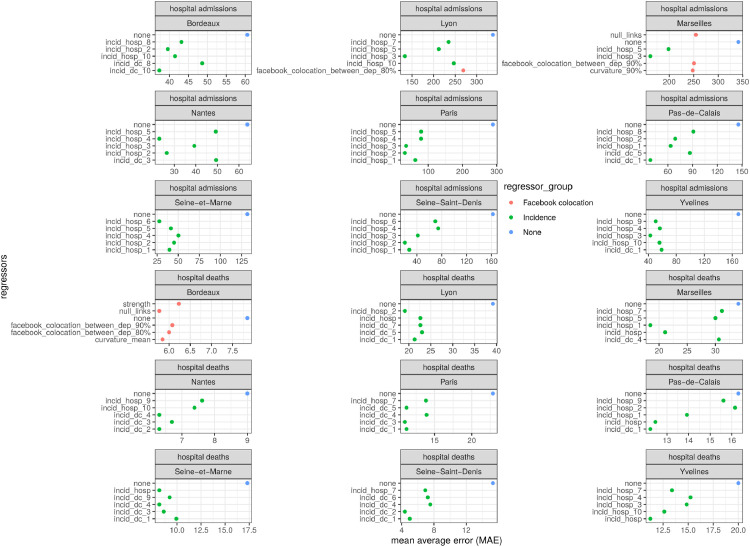
Performing the same analysis at the department level revealed the importance of spatial structure. In particular, for Paris region departments (Paris, Yvelines, Seine-Saint-Denis and Seine-et-Marne) and Nantes, the predictors that decreased the mean prediction error the most when compared with models without regressors were those related to the incidence in highly colocalized departments (Fig. 6 ). Conversely, for the metropolitan areas of Lyon, Bordeaux and Marseilles, network descriptors (in red) such as curvature and null links but also overall between-department colocation weights were among the best predictors of hospital admissions and deaths. This was also the case for 2-week predictions of local hospital deaths, and to a lesser extent for 2-week predictions of hospital admissions (Fig. 7 ).

Fig. 6.

Top-five 1-week predictive models for new department-level hospital admissions and deaths with the lowest mean average error using network analytics or incidence (’dc’ for death and ’hosp’ for hospital admission) of the top-10 colocated departments as regressors (numbers in subscripts). The colour code refers to the group of regressors used and the panels refer to the nine most populated departments used in the analysis.

Fig. 7.

Top-five 2-week predictive models for new department-level hospital admissions and deaths with the lowest mean average error using network analytics or incidence (’dc’ for death and ’hosp’ for hospital admission) of the top-10 colocated departments as regressors (numbers in subscripts). The colour code refers to the group of regressors used and the panels refer to the nine most populated departments used in the analysis.

4. Discussion

Numerous studies have reported potential insights that can be gained from mobile phone usage data so as to understand the spread of infectious diseases. However, these data are usually analysed from an individual perspective, by following where the users are and how they move. The Facebook Inc. data differ in that they contain colocation data. We hypothesized that such data could be particularly suited to understanding the transmission of respiratory infections, which involves close contact between individuals. To address this question, we developed an explicit network-based analysis of relevant summary statistics regarding colocation data.

Our analysis indicates that human mobility and contact data improve time series prediction of French COVID-19 hospital admissions and deaths by up to 50%. Determining a posteriori the optimal combination of regressors shows that human contact network analytics augmented with temperature and positive testing rate data yields perfect fits at the 1-week horizon. Although these combinations are not of a predictive nature, they highlight the impact of global network properties, which are a proxy for the extent of human contact in contrast to human mobility alone. Spatial disparities in disease incidence have motivated subnational policy decisions to manage the pandemic (Karatayev et al., 2020), and our subnational time series analysis confirms the predictive power of spatial structure since incidence from colocalized administrative units improved most incidence predictions. Notably, we find that human contact network analytics, such as curvature, null links and network strength, are prominent predictors for the metropolitan areas of Lyon, Bordeaux and Marseilles. Further investigations using a metapopulation point of view could yield additional insights.

Another asset of our study is that even though our 2-week prediction horizon is relatively long compared with the prediction horizons of other studies, it remains quite robust for predictions of hospital deaths when compared with 1-week predictions, even for a posteriori fits. This is also slightly the case for hospital admissions. The fact that peak incidence was systematically overestimated points to the weakness of using only linear models, especially in situations where the susceptible populations are rapidly depleted.

Our results reveal the contrasting importance of temperature fluctuations, since temperature was not included in the top univariate regressors, but improved a posteriori fits when combined with other regressors. One possible explanation could be that national and subnational policy changes over the period considered led to human contact mobility regressors being favoured over temperature in terms of explanatory power.

Our study has several limitations. First, by focusing on the elaboration of contact network analytics, we have used rather elementary statistical models. These have the advantage of being easy to interpret, but, given the number of features, more sophisticated machine learning techniques, such as long short-term memory neural networks or random forests, could allow more information to be extracted from the data. Second, the interpretation of colocation data as a proxy for infectious contacts remains to be validated in the field (e.g. in community transmission studies (Riley et al., 2021)). The validation would also require the importance of hospital catchment areas to be concurrently taken into account when disease incidence is recorded (Massonnaud et al., 2020). Furthermore, assortativity between users and user coverage might introduce biases that do not reflect the extent of human contacts pertaining to disease transmission. Although user coverage for colocation data showed important variations over time and between departments (Fig. S2), it remained constant during the period of resurging hospital incidence (i.e. between October 2020 and January 2021). It has been shown that combining census and survey data may help remove user bias related to sex, ethnicity and age (Ribeiro et al., 2020), but this would require access to individual-level information for colocation data.

Collectively, our time series analysis shows the potential of human contact network analytics to improve both predictions and a posteriori model fits of disease incidence as recorded during the COVID-19 pandemic in France. Combining network analytics with mechanistic models of disease transmission opens promising novel avenues for real-time disease control.

Funding source

The authors thank the CNRS, the IRD, the ANR and the Région Occitanie (PHYEPI project) for funding.

Ethical approval

Ethical approval or individual consent was not applicable.

CRediT authorship contribution statement

Christian Selinger: Conceptualization, Data curation, Formal analysis, Writing – original draft, Writing – review & editing, Validation. Marc Choisy: Conceptualization, Writing – review & editing, Validation. Samuel Alizon: Conceptualization, Writing – review & editing, Validation.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this article.

Appendix A. Supplementary materials

Supplementary Data S1

Supplementary Raw Research Data. This is open data under the CC BY license http://creativecommons.org/licenses/by/4.0/