Evolution reverses the effect of network structure on metapopulation persistence

Abstract

Global environmental change is challenging species with novel conditions, such that demographic and evolutionary trajectories of populations are often shaped by the exchange of organisms and alleles across landscapes. Current ecological theory predicts that random networks with dispersal shortcuts connecting distant sites can promote persistence when there is no capacity for evolution. Here, we show with an eco‐evolutionary model that dispersal shortcuts across environmental gradients instead hinder persistence for populations that can evolve because long‐distance migrants bring extreme trait values that are often maladaptive, short‐circuiting the adaptive response of populations to directional change. Our results demonstrate that incorporating evolution and environmental heterogeneity fundamentally alters theoretical predictions regarding persistence in ecological networks.

Introduction

The adaptive capacity of a species underlies its ability to persist in novel or actively changing environments. At a particular location, population‐level responses to new conditions are determined by ecological and evolutionary processes that are often tightly coupled through feedback loops (reviewed in Hanski [2012]). The eco‐evolutionary dynamics in spatially distinct subpopulations may also be linked within a regional‐scale metapopulation by individuals that disperse among sites. These subpopulations can occupy patches with biophysical characteristics that vary significantly, potentially favoring a wide array of optimal traits or trait values across the system (García‐Ramos and Kirkpatrick 1997, Kawecki 2004, Hereford 2009, Hanski et al. 2011). The dispersal network comprises demographic linkages among discrete sites, therefore dictating both demographic and genetic connectivity among subpopulations and shaping both their demographic and evolutionary trajectories. In light of rapid environmental change and mounting evidence that evolution occurs on ecological timescales (Reznick et al. 2004), it is critical to understand the influence of dispersal network characteristics on eco‐evolutionary processes.

Dispersal is a key mechanism determining population responses to environmental change (Hanski and Ovaskainen 2000, Hastings and Botsford 2006, Norberg et al. 2012, Urban et al. 2016). The pattern of dispersal among patches can control whether connectivity improves or degrades the ability of a metapopulation or network to persist. For example, a key feature of dispersal network structure is whether the connections among subpopulations are regular or random. In contrast with regular networks where connections are limited to nearest neighbors, random networks have shortcuts that reduce the average number of intermediary patches that connect any two subpopulations (Watts and Strogatz 1998). Subpopulations or patches within random networks exhibit asynchronous population dynamics that increase the overall stability of the metapopulation compared to regular networks without long‐distance connections (Holland and Hastings 2008). Furthermore, current ecological theory predicts that random networks lead to more complex connectivity loops that support greater persistence than regular networks (Holland and Hastings 2008, Artzy‐Randrup and Stone 2010, Grilli et al. 2015). However, the influence of evolution on metapopulation dynamics remains underexplored since most studies that link dispersal network structure to population persistence typically ignore evolutionary processes (but see Hanski and Mononen 2011, Thompson and Fronhofer 2019).

From an evolutionary perspective, the ability of a population to locally adapt is governed by the balance between gene flow and selection (Barton and Whitlock 1997, Hendry et al. 2001, Garant et al. 2007). Environmental heterogeneity also plays a role in local persistence: across a species range, populations in different environments may maintain significantly different trait values or genotypes (Kirkpatrick and Barton 1997) and populations can receive both advantageous and disadvantageous traits from immigrants adapted to different local conditions (Holt 1996, Holt and Gomulkiewicz 1997, Lenormand 2002, Holt et al. 2003, Kleypas et al. 2016). To that end, previous theoretical work in continuous space has shown that species range expansion can be prevented by maladaptive gene flow from larger, centrally located populations to smaller, peripheral populations (Haldane 1956, García‐Ramos and Kirkpatrick 1997, Kirkpatrick and Barton 1997) and that range boundary formation is largely mediated by the steepness of the environmental gradient (Barton 2001, Polechová and Barton 2015, Polechová 2018). However, these studies assume that movement along the species range is governed by diffusive migration, which is unsuitable for describing the dynamics of metapopulations with complex dispersal networks (Hanski 1998).

In this study, we explored the effects of dispersal network configuration on metapopulation persistence in a changing environment by incorporating directed dispersal among discrete habitat patches within an eco‐evolutionary model (Pease et al. 1989, Kirkpatrick and Barton 1997, Norberg et al. 2012). We tracked the abundance within subpopulations as a fraction of the local carrying capacity (i.e., “relative abundance”) as well as a quantitative trait, the mean thermal optimum, that determined fitness in the local environment and that could evolve based on selection (sensu Walsworth et al. 2019).

Model and Methods

Eco‐evolutionary metapopulation dynamics were computed on 20 habitat patches across a thermal gradient that spans 10°C (all simulated data and code are available; see Open Research statement). This framework is intended to simulate systems that span temperature gradients such as networks of coral reefs that are linked by ocean currents, or trees in forest fragments connected by seed dispersal. In the regular network, each subpopulation or patch was connected to itself and its four nearest neighbors. To produce random networks, we assigned connections between patches at random (Watts and Strogatz 1998, Holland and Hastings 2008); these links were fixed for the duration of the simulation and represented the demographic connections that occurred at each time step (Fig. 1A). As in the regular network, each patch in a random network was connected to exactly four other patches (i.e., degree = 4). Dispersal was symmetric, such that each connection defined both incoming and outgoing propagule contributions. We note that our full framework models connectivity, which includes both dispersal and survival to reproduction (in contrast with solely modeling dispersal). A summary of key parameters is presented in Table 1.

Fig. 1.

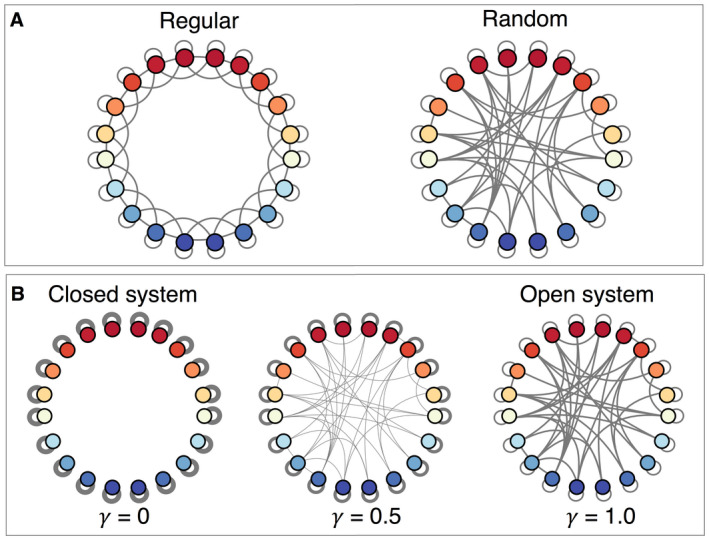
Schematic of regular and random dispersal networks. Warmer and cooler colors represent patches with higher and lower temperatures, respectively. (A) In the regular network, each patch is connected to its four nearest neighbors, while in the random network, connections are possible between any nodes, creating shortcuts. (B) A closed system (γ = 0) has isolated patches with only self‐connections while a fully open system (γ = 1) has equal dispersal probability among all connections, shown here for the random network from panel A.

Table 1.

Parameter definitions and values used in simulations.

Parameter	Value or range	Definition
ro	1.0	scaling factor for growth rate; note that maximum growth rate is $\frac{r_0}{\sqrt{2\mathrm{\pi }{w}^2}}$
w	1.5	thermal tolerance breadth
β	0.05	effective fecundity rate
V	0–0.2	additive genetic variance
γ	0–1.0	network openness

Eco‐evolutionary metapopulation model

We incorporated dispersal among discrete patches within a framework that tracked the eco‐evolutionary dynamics of a metapopulation experiencing temperature increase (Norberg et al. 2012, Walsworth et al. 2019). The equation governing the change in relative abundance (e.g., abundance as a fraction of carrying capacity) at each patch i is

$$\frac{d{N}_i}{\mathit{dt}}=g_i{N}_i+l_i\left(1‐N_i\right)+\frac{1}{2}V\frac{{\partial }^2{g}_i}{\partial z^2}{|}_{z=z_i}{N}_i,$$ (1)

where N_i is the relative abundance of the subpopulation. The first term on the right‐hand side of Eq. 1 dictates population dynamics, which are governed by the overall fitness of the species at patch i, g_i . The second term quantifies immigration into the patch through the immigration rate l_i , which is determined by reproductive output from the source patches and the dispersal network configuration (Hanski et al. 2011; see Appendix S1: Section S2 for derivation). The establishment of new individuals also slows as relative abundance approaches 1. The last term represents the genetic load, which depends on the mean trait value of the subpopulation, z_i , and the additive genetic variance, V. Higher V makes rapid evolution possible (Lande 1976) but also leads to a greater genetic load (Kirkpatrick and Barton 1997). Due to the concavity of the fitness curve with respect to the average trait value and local temperature, genetic load is either negative or zero.

The change in trait value (z_i ), here the optimum growth temperature, for the subpopulation at patch i is

$$\frac{d{z}_i}{\mathit{dt}}=\left(z_i^c‐z_i\right)\left(\frac{l_i}{N_i}\right)(1‐N_i)+q_{i}V\frac{\partial g_i}{\partial z}{|}_{z=z_i},$$ (2)

where the first term on the right‐hand side represents the effect of gene flow and the second term quantifies the effect of stabilizing selection. Here, the current trait is subtracted from $z_i^c$, the population‐weighted mean trait of immigrating individuals based on the migrant pool model of colonization (Hanski et al. 2011). This trait difference is then scaled by the fraction of relative abundance represented by new immigrants (l_i /N_i ) (i.e., density dependence). In the second term, the effects of stabilizing selection are reduced by q_i at low abundance.

The overall fitness of the species at patch i (g_i ) is

$$g_i=r_i\left(1‐N_i\right)‐m_i,$$ (3)

where r_i is the population's intrinsic growth rate and m_i is the mortality rate. Population growth is density dependent and slows as relative abundance approaches 1. The maximum growth and mortality rates are given by

$$r_i=\frac{r_0}{\sqrt{2\mathrm{\pi }{w}^2}}\exp \left(\frac{‐\left(T_i‐z_i\right)}{w^2}\right)\text{and}$$ (4)

$$m_i=\left\{\begin{array}{cc}0,& T_i\le z_i\\ 1‐\exp \left(\frac{‐\left(T_i‐z_i\right)}{w^2}\right),& T_i>z_i\end{array}\right..$$ (5)

The maximum growth rate is modeled as a Gaussian tolerance function (Norberg et al. 2012, Kremer and Klausmeier 2017) where maximum subpopulation growth occurs when the local average trait value, z_i , perfectly matches the local temperature T_i . The width of thermal tolerance is denoted as w, and r ₀ is a growth scaling factor such that $r_0/\sqrt{2\mathrm{\pi }{w}^2}$ is the maximum growth rate. Following Walsworth et al. (2019), we impose additional mortality when the current local temperature exceeds the optimum growth temperature, T_i  > z_i . The additional mortality imposes higher costs for temperatures hotter than the optimum, as compared to temperatures colder than the optimum, consistent with the skewed thermal performance curves observed in most species (Deutsch et al. 2008).

In addition to this skew Gaussian function, another common approach to modeling fitness (analogous to combined growth and mortality in our model) is to use a quadratic formulation since this leads to simple and exact equations under strong selection as long as the population’s mean trait is close to the optimal value (e.g., Lande 1976, Kirkpatrick and Barton 1997). To test the sensitivity of our results, we also implemented this alternative quadratic formulation for growth (see Appendix S1: Section S3). In general, trait‐based eco‐evolutionary models typically assume that maximum growth is a unimodal function of trait, which is satisfied by both Gaussian and quadratic functions. We note that while the exact shapes of fitness functions remain largely unknown (Klausmeier et al. 2020, Osmond and Klausmeier 2017), both types explored here can locally approximate any smooth, general fitness function (Shaw and Geyer 2010).

The change in abundance through time is also affected by the dispersal of individuals across the network. Our model differs from previous frameworks (Norberg et al. 2012, Walsworth et al. 2019) since we incorporate spatially explicit dispersal among patches instead of a diffusion approximation. Immigration or propagule input (l_i ) is calculated from the abundance on other patches, the effective fecundity rate β, and the connectivity matrix D in which element D _ij is the probability of reaching patch i from patch j

$$l_i=\mathrm{\beta }\sum _j{\mathrm{D}}_{\mathit{ij}}{N}_j.$$ (6)

Local evolution is governed in part by gene flow (first term in Eq. 2). The population‐weighted mean trait value of immigrants is given by $z_i^c$

$$z_i^c=\frac{\mathrm{\beta }\sum _j{\mathrm{D}}_{\mathit{ij}}{N}_j{z}_j}{l_i}.$$ (7)

Finally, at very low abundance, (N _min = 1 × 10⁻⁶), q_i reduces the effect of stabilizing selection:

$$q_i=max\left(0,1‐\frac{N_{min}}{max\left(N_{min},2N_i\right)}\right).$$ (8)

Temperature increase experiments

To test the effects of directed environmental change on the metapopulation, we simulated increasing temperatures that plateaued after approximately 200 yr, though we solved for the dynamics through 500 yr. Initial conditions for these experiments were generated by burn‐in runs of 1,500 yr at constant temperatures; burn‐ins were initialized with N = 0.25 across all patches. For each run, we incorporated stochastic temperature anomalies that were equivalent across the network.

We explored different levels of openness γ, here defined as the potential contribution of individuals from outside the patch vs. from within the patch. We modified openness with D′ = γD + (γ−1)I, where D′ is the modified connectivity matrix and I is the identity matrix. The fully open system (γ = 1.0) represents the baseline network where self‐connection and external connection strength are equal (i.e., each of the five connections has a strength of 0.2). In the fully closed system (γ = 0), self‐recruitment strength is 1.0 and no external connections exist; this represents a network of isolated patches (Fig. 1B). In addition to openness, we also explored different levels of additive genetic variance V. For every parameter combination of γ and V, we simulated 20 runs each for the regular and random networks; results shown are average values. Note that we used a total of 20 random network configurations and a single regular network, although temperature anomalies were uniquely generated for each run. Finally, to test the effects of environmental steepness, we completed simulations for systems that spanned different thermal gradients: 0°, 5°, and 20°C (see Appendix S1: Section S1). Results shown are for the 10°C thermal gradient.

Trait mismatch

A key complexity introduced by evolutionary dynamics is that dispersal can affect local trait values in networks (Lenormand 2002). Some immigrants, for example, may have traits that are maladapted to a new patch. An informative summary of network structure, therefore, is the difference between the locally optimal trait value and the average trait values of immigrants, which we term ‘trait mismatch’ (Eq. 9). Here, n is the total number of patches that are connected to patch i (in our case, n = 4)

$${\text{trait mismatch}}_i=\frac{\sum _j|T_i‐z_j|{\widehat{\mathrm{D}}}_{\mathit{ij}}}{n},$$ (9)

where the scaled connectivity matrix, $\widehat{\mathbf{D}}$, is calculated by dividing the connectivity matrix by the element with the largest value, max(D) such that the maximally strongest connection in $\widehat{\mathbf{D}}$ is 1

$$\widehat{\mathbf{D}}=\frac{\mathbf{D}}{max(\mathbf{D})}.$$ (10)

Results

At the network scale, we found that the genetic variance (V), which sets evolutionary potential, strongly interacted with dispersal structure to influence population persistence. With no evolutionary capacity (V = 0), random networks had greater abundance than regular networks (Figs. 2A and 2B). In contrast, higher genetic variance flipped these effects: when evolutionary potential was high, regular networks led to consistently higher abundance under systems with high and low openness (V ≥ 0.06, Figs. 2A, B). Evolutionary capacity also influenced abundance under increasing temperature scenarios: while random networks performed better with no evolutionary potential (V = 0; Figs. 2C, D), regular networks performed better with both strong (V = 0.2) and weak (V = 0.06) evolutionary capacity and low openness (Figs. 2C, D). In both network types, final relative abundance was higher with increased V (Fig. 3). During constant temperature experiments, increasing steepness of the environmental gradient (i.e., increasing the temperature range across the network) led to lower abundance across all levels of genetic variance, although this effect was less pronounced in the regular network (Appendix S1: Fig. S1). Under increasing temperatures and no evolution, however, metapopulations with gradients of 10° and 20°C maintained abundance while systems with a 0° and 5°C thermal range experienced extinction (Appendix S1: Fig. S1).

Fig. 2.

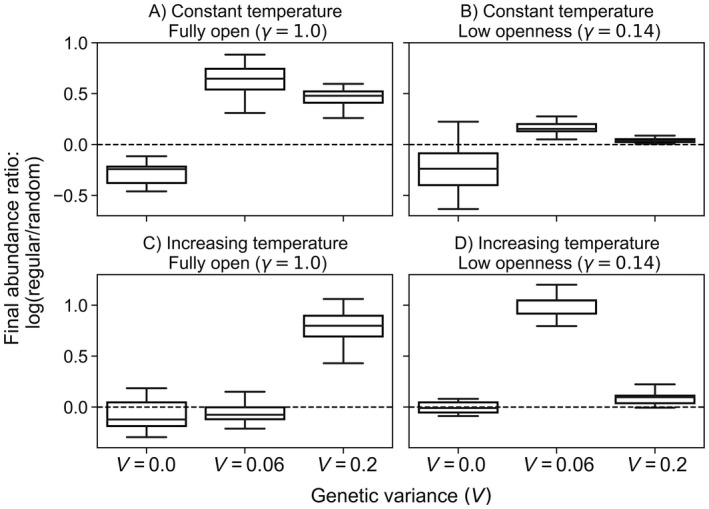
Influence of genetic variance on network‐wide mean abundance at different levels of system openness. Results above the dashed horizontal line indicate that final abundance is higher in regular than random networks while results below the line indicate the opposite. Note the change in scale between top and bottom rows.

Fig. 3.

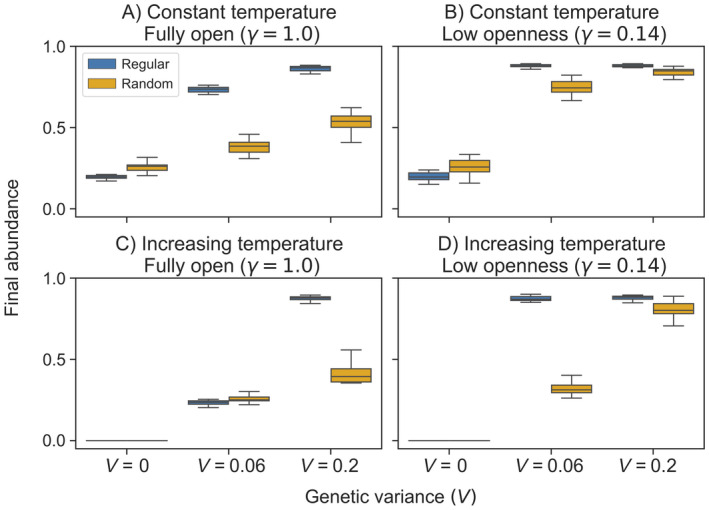
Final mean abundance across regular and random networks under (A, B) constant and (C, D) increasing temperature scenarios. Results are shown for two levels of openness under three levels of additive genetic variance.

Initially cold patches either maintained greater abundance during temperature increase or recovered faster once temperature stabilized relative to the rest of the network. Overall patterns of abundance were largely associated with differences in the local dynamics in relatively warm patches; these subpopulations were more likely to maintain abundance in regular than in random networks (Figs. 4A and 4B, Appendix S1: Figs. S2 and S3). In general, subpopulations in systems with regular dispersal networks were better able to match mean optimal temperature to local environmental values (Figs. 4C and 4D).

Fig. 4.

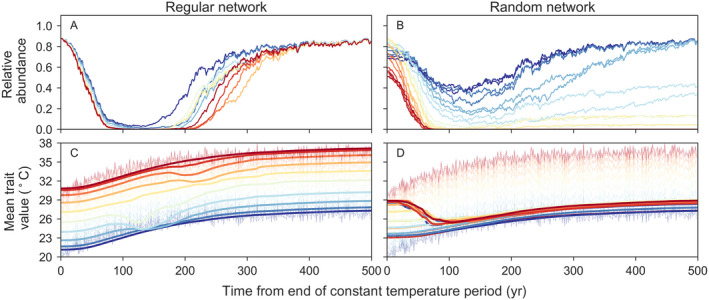
Illustrative trajectories of (A, B) relative abundance and (C, D) mean trait value (optimum growth temperature) by patch for regular and random networks. Simulations during the temperature increase period are for a system with low openness (γ = 0.14) and low additive genetic variance (V = 0.06). Trajectories are colored by relative patch temperature, where warmer and cooler colors represent higher and lower temperatures, respectively. Lines are mean trajectories averaged across 20 runs. Translucent lines in the bottom row are the temperature time series.

We found that these results were robust to the choice of fitness functional form. Under the assumption of quadratic fitness, random networks led to greater abundance at low V, but regular networks led to greater abundance at higher V (Appendix S1: Figs. S4 and S5). In addition, regular networks promoted local adaptation while random networks were susceptible to gene swamping from sites with the highest abundance. This was evident in the maintenance of a wide set of trait values in the regular network and a narrowing of values in the random networks (Appendix S1: Fig. S6).

At a given patch, trait mismatch depended on source patch conditions and openness; on average, random networks experienced higher trait mismatch at a given openness, and this discrepancy was largest in fully open systems (Fig. 5). High trait mismatch values signified that patches received larvae that were relatively maladapted to current local conditions (i.e., temperature), inhibiting local adaptation. In the eco‐evolutionary simulations, low trait mismatch at the start of the simulation was associated with higher levels of relative abundance and more local adaptation (measured as trait standard deviation across the network) at the end of the simulation for both network types (Fig. 5). High trait standard deviations, in particular, signaled low gene swamping and strong local adaptation (Fig 5A).

Fig. 5.

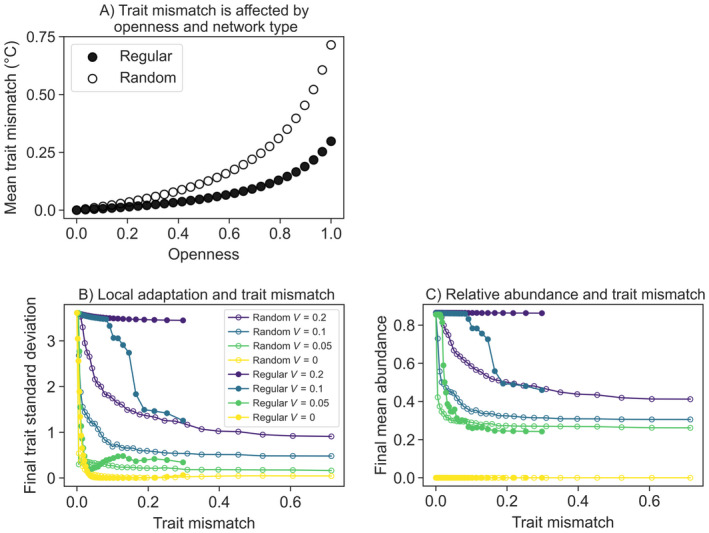
Relationship between trait mismatch and eco‐evolutionary dynamics. (A) Trait mismatch is the difference between optimal and average potential incoming trait values, and is affected by network type and openness. Results are shown for initial temperature conditions in the regular (filled circle) and random (open circle) dispersal networks. (B) Greater degrees of local adaptation (measured as final trait standard deviation across the network) and (C) higher mean abundance were associated with lower levels of trait mismatch. Filled and open circles are results from regular and random network configurations, respectively. Line colors are different values of genetic variance (V): V = 0 (red), V = 0.07 (orange), V = 0.1 (green), and V = 0.2 (blue).

Discussion

We find that the relative performance of populations in the two dispersal network configurations ultimately depends on evolutionary capacity, openness, and the strength of environmental change. From a purely demographic perspective, random dispersal is beneficial since abundant subpopulations can rescue depleted subpopulations through connectivity shortcuts across the network. In contrast, regular networks (and relatively closed networks, in general) are beneficial from an adaptation perspective because they reduce gene swamping. In support of this conclusion, there is empirical evidence that genetic connectivity among populations with similar environments is relatively common in nature (Sexton et al. 2014). Furthermore, in a flowering plant species, connectivity between geographically distant locations with equivalent climatic conditions are more likely to increase reproductive success than gene flow between environmentally distinct habitats within the same transect (Sexton et al. 2011).

Most studies that relate connectivity to persistence focus on metrics of system‐wide demographic effects such as centrality and degree‐distribution (i.e., number of incoming or outgoing links) (Ovaskainen and Hanski 2003, Jacobi and Jonsson 2011, Watson et al. 2011, Kininmonth et al. 2019). Our work underscores the importance of focusing not only on network structure, but also on the interaction of the network with environmental heterogeneity. For example, while steeper environmental gradients generally led to lower abundance, a wider thermal range facilitated persistence in populations with low evolutionary capacity under increasing temperatures. With these conditions, a narrow environmental gradient led to extinction. Solely accounting for the distribution and number of dispersal links therefore leads to an incomplete understanding of persistence. In other words, the genetic or phenotypic characteristics of connected subpopulations must be taken into account when assessing adaptive capacity, particularly under changing environmental conditions.

The opposing effects of genetic variance and network structure on overall population abundance arise from eco‐evolutionary feedbacks. Initially cold patches typically fared better relative to warmer patches, in part because the influx of warm‐adapted propagules facilitated local adaptation (Fig. 4 and Appendix S1: Fig. S2). Asymmetries among subpopulations can also constrain local adaptation at marginal sites because of gene flow (Dias and Blondel 1996, García‐Ramos and Kirkpatrick 1997). As populations in initially cold habitats became disproportionately abundant, they also exported more cold‐adapted propagules. In regular networks, migration across the environmental gradient required more steps: the hottest patches did not directly receive propagules from the coldest patches, which allowed for selection to act (Holt and Gaines 1992, Holt and Gomulkiewicz 1997, Kawecki 2004), facilitated local adaptation at hot sites, and increased overall abundance and persistence.

Initially hot patches faced an adaptive disadvantage in random networks because a substantial fraction of incoming propagules had genetic traits unsuited to these habitats; the influx of propagules from cold‐adapted populations reduced the adaptive capacity in warm habitats, leading to local extinction (Appendix S1: Fig. S3; Ronce and Kirkpatrick 2001). This eco‐evolutionary feedback between dynamic population abundance and local selection further strengthened the role of cold patches as sources and warm patches as sinks, reflecting dynamics driven by asymmetries and that adaptation tends to favor the environment experienced by the greatest number of individuals (Holt and Gaines 1992).

The primary driver of these patch‐level differences (i.e., warm vs. cold) was the directionality of environmental change; under increasing temperatures, cold and warm patches were effectively the leading and trailing edges of the species' distribution, respectively. As warming occurred, pre‐adapted propagules from warmer subpopulations in the network supported the growth of subpopulations in colder patches. However, at the warmest patches, no pre‐adapted propagules existed, while colder, maladapted immigrants were detrimental to population growth. Instead, hot patches solely relied on in situ evolution to select for traits that could persist in novel warming conditions. These dynamics support previous results showing that selection dominates the response to warming at already warm sites due to the lack of pre‐existing adaptive traits in the system (Norberg et al. 2012).

Our results underscore that the extent to which individuals disperse across environmental gradients is critical to the adaptive capacity of populations. This characterization requires an understanding of life history within the context of environmental conditions. For example, in corals, broadcast spawner larvae can travel tens to thousands of kilometers before settlement (Richmond 1997, Connolly and Baird 2010, Wood et al. 2014) while brooder larvae typically settle near the parent colony (Richmond 1997). In plants, seeds that are ingested and transported by large vertebrates generally travel distances that are orders of magnitude greater than those that are wind‐dispersed (Vittoz and Engler 2007). If dissimilarities in habitat conditions increase with geographic distance, connectivity patterns for these organisms characterized by short‐ and long‐distance dispersal could approximate regular and random networks, respectively. However, in both terrestrial and marine systems, habitat types are often patchily distributed; adjacent sites can be vastly different and environmentally similar sites can be separated by thousands of kilometers. In general, adaptive capacity at the network and patch scales will depend on the focal landscape and the levels of trait mismatch that result from connectivity patterns. By extension, our work suggests that the success of conservation efforts such as assisted migration depends on the matching of trait values between source populations and recipient environments.

Our modeling approach included some necessary and important simplifying assumptions. First, because we modeled dispersal as a static probability, the model is particularly applicable to organisms that disperse early in their life history and remain in their settlement patch for the rest of their lifetimes. While sessile populations such as corals and plants are obvious examples, this framework should also be applicable to reef fishes, insects, non‐migratory birds, freshwater crustaceans, and microbes. Second, we assumed that local subpopulation dynamics were identical across patches except for the source patch identities of immigrants and the temperatures experienced. While this assumption facilitated our exploration of evolutionary and environmental effects, real systems are far more heterogeneous. Patches could differ along several axes including habitat quality and community composition, both of which would affect the local carrying capacity. Third, we did not consider the effects of genetic drift, which can determine species range limits (Polechová and Barton 2015) and as such, we implicitly assume that local populations are sufficiently large (Kirkpatrick and Barton 1997). Finally, some dispersing individuals select their destination habitats based on phenotype‐habitat matching (Marshall et al. 2010, Hanski et al. 2011). Such settlement bias leads to a higher match between the environment and optimal phenotype than would be otherwise expected (Hanski et al. 2011), and is a dispersal behavior that effectively results in more regular networks in nature. While not examined here, similar approaches can also be used to examine multiple species and assess the adaptive response of entire communities (Norberg et al. 2012, Urban et al. 2016).

To better understand the consequences of ongoing global environmental change on ecosystems, it is important that we consider processes that promote or constrain adaptive capacities of metapopulations. While dispersal shortcuts across environmental gradients benefit populations when evolution is weak, such connections reduce adaptive capacity when populations can evolve more rapidly. A coherent framework incorporating ecology, evolution, and network features is essential to understand how species respond to anthropogenic stressors and conservation efforts.

Supporting information

Appendix S1

McManus, L. C., Tekwa E. W., Schindler D. E., Walsworth T. E., Colton M. A., Webster M. M., Essington T. E., Forrest D. L., Palumbi S. R., Mumby P. J., and Pinsky M. L.. 2021. Evolution reverses the effect of network structure on metapopulation persistence. Ecology 102(7):e03381. 10.1002/ecy.3381

Open Research

All simulated data and code are available on Zenodo: https://doi.org/10.5281/zenodo.4620329.