Abstract
The inference of cortical sulcal labels often focuses on deep (primary and secondary) sulcal regions, whereas shallow (tertiary) sulcal regions are largely overlooked in the literature due to the scarcity of manual/well-defined annotations and their large neuroanatomical variability. In this paper, we present an automated framework for regional labeling of both primary/secondary and tertiary sulci of the dorsal portion of lateral prefrontal cortex (LPFC) using spherical convolutional neural networks. We propose two core components that enhance the inference of sulcal labels to overcome such large neuroanatomical variability: (1) surface data augmentation and (2) context-aware training. (1) To take into account neuroanatomical variability, we synthesize training data from the proposed feature space that embeds intermediate deformation trajectories of spherical data in a rigid to non-rigid fashion, which bridges an augmentation gap in conventional rotation data augmentation. (2) Moreover, we design a two-stage training process to improve labeling accuracy of tertiary sulci by informing the biological associations in neuroanatomy: inference of primary/secondary sulci and then their spatial likelihood to guide the definition of tertiary sulci. In the experiments, we evaluate our method on 13 deep and shallow sulci of human LPFC in two independent data sets with different age ranges: pediatric (N = 60) and adult (N = 36) cohorts. We compare the proposed method with a conventional multi-atlas approach and spherical convolutional neural networks without/with rotation data augmentation. In both cohorts, the proposed data augmentation improves labeling accuracy of deep and shallow sulci over the baselines, and the proposed context-aware training offers further improvement in the labeling of shallow sulci over the proposed data augmentation. We share our tools with the field and discuss applications of our results for understanding neuroanatomical-functional organization of LPFC and the rest of cortex (https://github.com/ilwoolyu/SphericalLabeling).
Keywords: Context encoder, Cortical surface, Frontal cortex, Spherical data augmentation, Sulcal labeling
1. Introduction
Indentations in the outer surface of the cerebrum, known as sulci, are key phenotypical biomarkers for linking brain structure and function (Armstrong et al., 1995; Cachia et al., 2008; De Winter et al., 2015; Huang et al., 2020; Le Goualher et al., 1999; Lyu et al., 2018a; 2018b; Mangin et al., 2004; Miller et al., 2020b; Weiner et al., 2014; Welker, 1990; Zilles et al., 1988). It is well known that deep sulci, which emerge early in gestation, are key landmarks linking structure, function, and behavior in primary sensory cortices (Armstrong et al., 1995; Ono et al., 1990; Sanides, 1964; Schwarzkopf and Rees, 2013; Welker, 1990). By contrast, studies have recently begun to show that shallow, tertiary sulci, which emerge late in gestation (Chi et al., 1977; Welker, 1990), are key landmarks in association cortices (Amiez et al., 2020; Lopez-Persem et al., 2019; Miller et al., 2020b; Voorhies et al., 2020a; Weiner, 2019; Weiner et al., 2014)1. These latter studies manually defined hundreds to thousands of tertiary sulci as a majority of present tools do not fully support labeling of fine-grained tertiary sulci in all association cortices yet. Nevertheless, steady improvements of previous tools are bringing us closer to achieving this goal (Borne et al., 2020; Cointepas et al., 2001; Joshi et al., 2012; Le Goualher et al., 1999; Lyu et al., 2010; Mangin et al., 1995; Parvathaneni et al., 2019b; Perrot et al., 2008; Rettmann et al., 2002; Riviere et al., 2002; Sandor and Leahy, 1997; Shattuck et al., 2009; Shi et al., 2009; Tao et al., 2002; Tu et al., 2007; Yun et al., 2019). Importantly, quantifying the precise morphology of tertiary sulci also has translational applications. For instance, recent studies show that morphological features of a tertiary sulcus in anterior cingulate cortex predicts whether an individual with schizophrenia will hallucinate or not (Garrison et al., 2015). Additionally, features of a tertiary sulcus in inferior frontal cortex are distinct in individuals with autism spectrum disorder (ASD) compared to individuals without ASD (Brun et al., 2016). Finally, ongoing work shows that the morphology of a tertiary sulcus in ventral temporal cortex is different in those who cannot perceive faces (developmental prosopagnosiacs) compared to those with typical face processing ability (Parker et al., 2020). Thus, developing tools to automatically identify tertiary sulci is critical for expediting the rate of progress in understanding how features of tertiary sulci relate to the functional organization of association cortices and cognition especially because tertiary sulci are hominoid-specific structures and associated with human-specific aspects of cognition (Armstrong et al., 1995; Borne et al., 2020; Miller and Cohen, 2001; Petrides, 2018; Voorhies et al., 2020a; Weiner, 2019; Welker, 1990).
A promising way forward to achieve this goal is convolutional neural networks (CNNs) that have recently shown remarkable achievement in image segmentation over traditional machine learning techniques. Despite their success, a majority of CNN architectures are restricted in their capability to be only optimized for Euclidean image grids. Such approaches cannot fully encode cortical surface data (2-manifold equivalent to a genus-zero topology) represented by a non-uniform grid without arbitrary cut of the original surface (i.e., topological change; broken neighborhood associations). In this context, spherical CNNs have become more popular to handle spherical data (Cohen et al., 2018; Esteves et al., 2018; Jiang et al., 2019; Kondor et al., 2018; Kondor and Trivedi, 2018; Perraudin et al., 2019; Seong et al., 2018). These architectures can learn spherical convolutional filters as a part of their training with valid spherical parametrization.
CNNs generally tend to improve performance as training samples increase (Hauberg et al., 2016; Nalepa et al., 2019; Shorten and Khoshgoftaar, 2019; Uzunova et al., 2017; Wilms et al., 2017; Zhao et al., 2019). Data augmentation also helps address the scarcity of training samples through geometric transformations (e.g., rotation, translation, etc.) that generate extra (free) samples (Shorten and Khoshgoftaar, 2019). However, geometric transformations may not be fully utilized for spherical data mainly due to the nature of the spherical space, in which geometric transformations are restricted; rotation and flipping are the only available options that enable limited variations of the training samples (i.e., global positional changes). Recent advances in volumetric data augmentation offer reasonable approximation of sampling (feature) space via statistical shape modeling (Uzunova et al., 2017; Wilms et al., 2017) or local transformation/diffeomorphism (Hauberg et al., 2016; Nalepa et al., 2019; Zhao et al., 2019), over which new training samples are generated. To the best of our knowledge, little advanced work is present yet in surface (spherical) data augmentation as this further requires the encoding of spherical deformation into a tractable feature space as well as efficient computation to draw samples from that space, which we aim to efficiently address here through decomposable deformation.
In addition to data augmentation, context-aware training may also help improve the automatic definition of small, variable cortical folds like tertiary sulci. Specifically, recent research shows that context encoders offer localized information for context-aware training and this approach is actively adaptive in image segmentation, as well as image reconstruction (Gu et al., 2019; Kim et al., 2013; Salehi et al., 2017; Tu and Bai, 2009; Xiang et al., 2017). Consequently, modelling the biological relationship between deep, primary/secondary sulci and shallow, tertiary sulci with context encoders has the potential to improve the inference of tertiary sulci that are also more variable in size and location than primary/secondary sulci as shown in Fig. 1. For example, a key neuroanatomical observation is that the hierarchical emergence of sulci (primary: first; secondary: intermediate; tertiary: last) reflects their prominence (primary: large and deep; secondary: intermediate in both depth and surface area; tertiary: small and shallow). Thus, it could be natural to infer sulci in a top-down manner as proposed in earlier work for volumetric cortical segmentation (Asman and Landman, 2014). In this way, primary/secondary sulci could act like spatial markers and serve as a series of priors to guide annotation of tertiary sulci (Barkovich, 2005; Ono et al., 1990; Sanides, 1964).
Fig. 1.
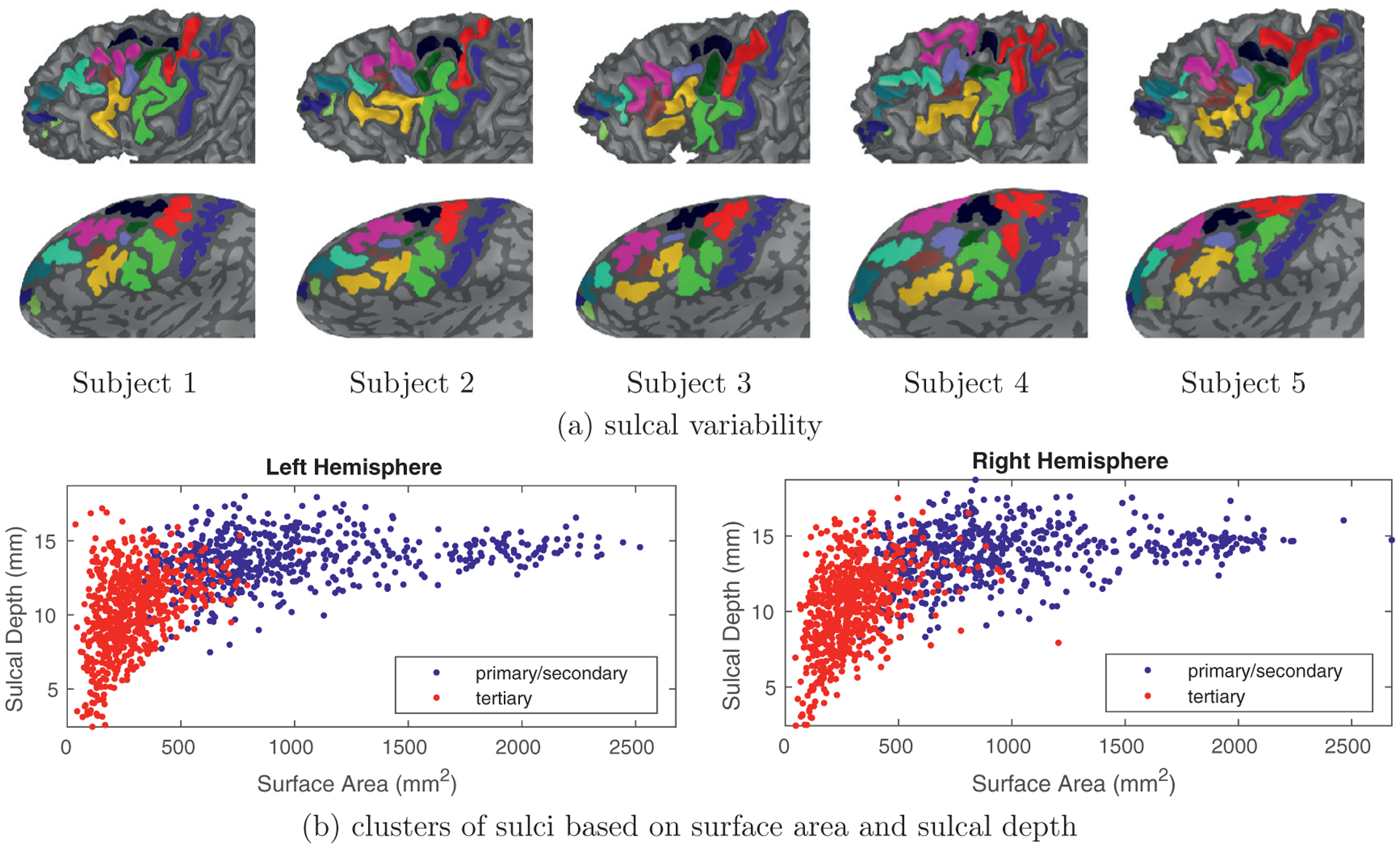
Primary, secondary, and tertiary sulci in LPFC emerge at different timepoints in gestation and are related to morphological variability in surface area and sulcal depth. (a) white matter (top) and inflated cortical surfaces (bottom) from five individual subjects zoomed in on LPFC in the left hemisphere. Light gray vertices are sulci, dark gray vertices are gyri, and colors indicate manually identified primary/secondary and tertiary sulci. Sulci in LPFC, especially tertiary sulci, have high spatial variability as well as various branches that differ across individuals as well as between hemispheres in the same individual. This variability makes it challenging to manually label sulci in LPFC, as well as generate automated tools that accurately define LPFC tertiary sulci. (b) sulci in LPFC can be clustered into different categories based on the point in which they emerge in gestation: primary sulci emerge first, while tertiary sulci emerge last and secondary sulci emerge in between. Interestingly, these gestational timepoint differences are also related to morphological differences: primary sulci are largest (in terms of surface area) and deepest, while tertiary sulci are typically smallest, and also shallowest, while secondary sulci are in between. We consider two groups in the present work: primary/secondary sulci (blue) and tertiary sulci (red) as determined by modern and classic neuroanatomy studies (Armstrong et al., 1995; Chi et al., 1977; Connolly, 1950; Cunningham, 1892; Miller et al., 2020b; 2020c; Retzius, 1896; Sanides, 1962; 1964; Weiner, 2019; Weiner et al., 2014; Weiner and Zilles, 2016; Welker, 1990). Each data point indicates total surface area and average sulcal depth per sulcus in LPFC. A total of 13 sulci from 96 subjects are used for this visualization. See Table 1 for details of the labeling protocol and Section 3.1 for the data collection.
In this paper, we focus on sulci in lateral prefrontal cortex (LPFC) for two main reasons. First, previous studies indicate extensive individual differences in the structural and functional organization of LPFC (see Fig. 1). This variability makes LPFC a good target to develop methodological tools because if the tools are effective in LPFC, they will likely generalize to other cortical areas that exhibit less variability. Second, ongoing work shows that LPFC tertiary sulci (a) serve as mesoscale links between microstructural anatomical properties and functional networks (Miller et al., 2020b) and (b) predict reasoning skills and working memory in children (Voorhies et al., 2020b; Yao et al., 2020). Hence, we extend our earlier work (Hao et al., 2020) to the labeling of primary/secondary and tertiary sulci in LPFC to address the following questions:
Does spherical deformation enhance spherical data augmentation to improve labeling accuracy of both primary/secondary and tertiary sulci in LPFC?
Does the inclusion of context-aware training improve performance when defining tertiary sulci in LPFC over spherical data augmentation?
To address both of these main questions, we adapt spherical CNNs designed for generic semantic segmentation tasks. Two key modifications are needed because generic spherical CNNs lack hierarchical neuroanatomical association and do not adequately capture anatomical variability with limited training samples. To adapt the generic networks, we propose spherical data augmentation as well as context-aware training to efficiently utilize existing training samples and to accept a wide range of individual variability by considering training data synthesis and contextual information. Additionally, we apply our method to identify 7 tertiary sulci in LPFC for the first time. As these sulci vary considerably across individuals and even between hemispheres in the same individual (Miller et al., 2020b; 2020c; Voorhies et al., 2020b), our method has the potential to allow researchers to make sense of this variability through automated definitions. The main contributions of this paper can be summarized as follows: (a) spherical data augmentation with detailed methodology, (b) context-aware training with spatial prior information of primary/secondary sulci, and (c) extensive evaluation of deep (primary/secondary) and shallow (tertiary) sulci in LPFC in both pediatric and adult cohorts.
2. Methods
2.1. Problem statement
The goal of the present study is to develop decomposable deformation-based spherical data augmentation as well as context-aware training informed by biological associations in neuroanatomy. More formally, for a cortical surface , we can extract N distinct feature maps with meaningful geometry (e.g., mean curvature) denoted by {F1, ⋯, FN} from a feature space such that . Given a collection Z of sulcal labels on Ω, consider a functional . Then, likelihoods that belong to each sulcal label can be written by
| (1) |
Once fN is optimized, the cortical labels can be determined by finding maximum likelihoods of . Here, fN (model) is a realization of machine learning techniques that infer Z from a part of ; a full collection of is implausible in practice. In general, the inference becomes more robust by controlling the model complexity (or domain-specific design) of fN and/or generalizing by increasing the sample size.
In this work, we use spherical CNNs designed for vertex-wise inference (so-called spherical U-Net) (Jiang et al., 2019) to solve fN. Our approach focuses on data augmentation (i.e., approximation of ) and retrieval of a priori to enhance generalizability in a trained instance of the existing architectures rather than structural development over existing ones. In particular, the proposed data augmentation offers a generic process that does not necessarily depend on a specific spherical CNN architecture. In the remainder of this section, we describe three main steps of sulcal labeling: (a) generation of augmented samples (pre-processing), (b) a priori computation of primary/secondary sulci (training strategy), and (c) spatial coherence improvement (post-processing). Fig. 2 illustrates a schematic overview of the proposed method.
Fig. 2.
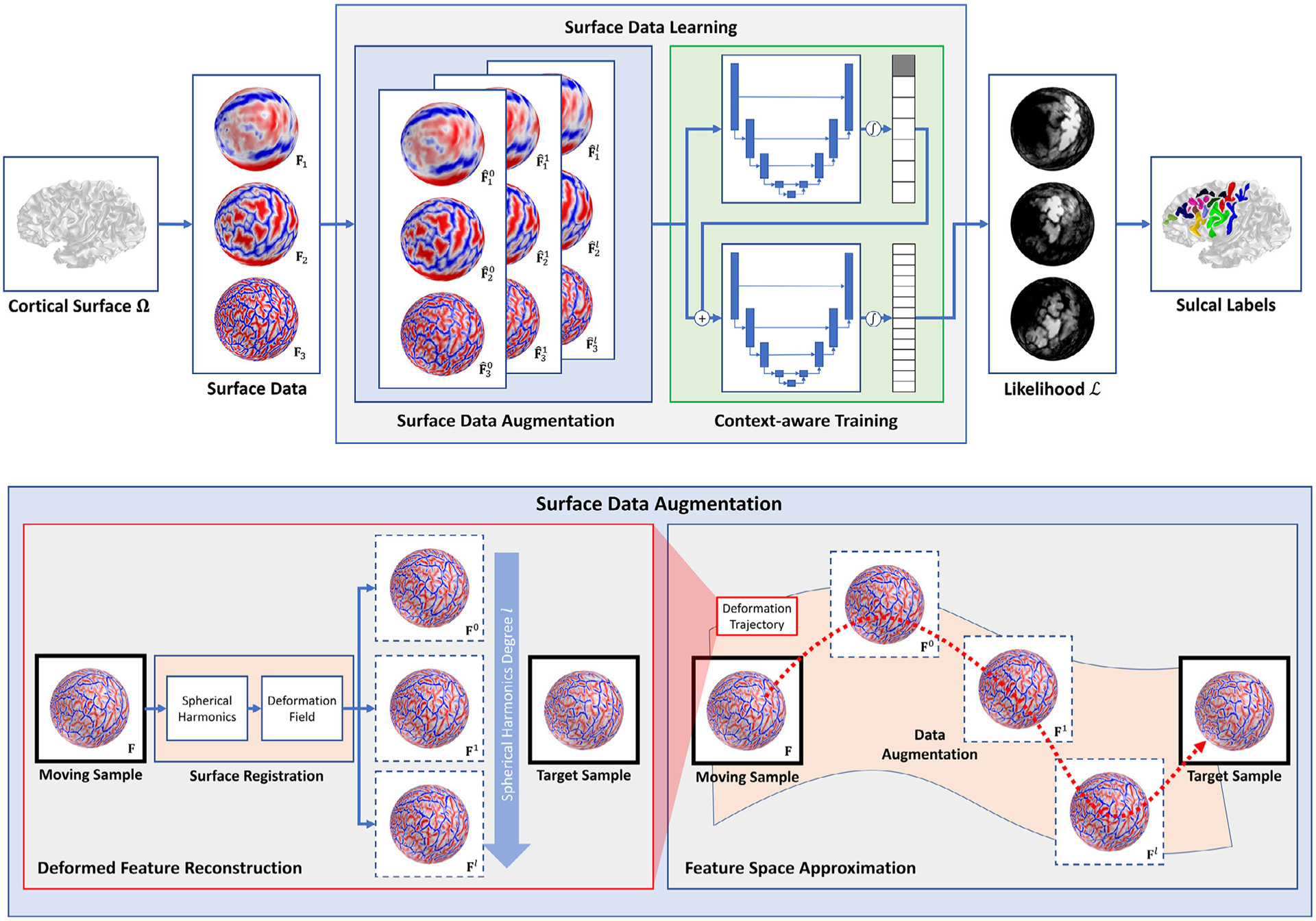
A schematic overview of the proposed method. Our method consists of two main components in the learning phase: surface data augmentation (blue box) and context-aware training (green box). During data augmentation, we augment training samples (dotted box) by deforming surface data over the sphere via surface registration to every possible pair of training samples. We decompose spherical deformation via the spherical harmonics and reconstruct its intermediate deformation by controlling the basis functions. In this way, a gap can be filled between moving and target samples in the feature space along their deformation trajectory (red). In the context-aware training, spatial information of primary/secondary sulci are inferred to guide labels of tertiary sulci. The information except for the background label (gray node in the output likelihoods) is then fed into the second training stage to offer spatial clues to guide the labeling of tertiary sulci. Note that the sulcal labeling in the test phase does not use registered (deformed) surface data, which allows fast annotation.
2.2. Surface data augmentation
2.2.1. Decomposable spherical deformation
We focus on deformation trajectories encoded by spherical harmonics that can model a smooth transition from rigid to non-rigid deformation. In general, cortical surfaces are enforced to be equivalent to a genus-zero in modern cortical surface reconstruction pipelines (Cointepas et al., 2001; Dale et al., 1999; Kim et al., 2005). As our focus is on the use of spherical data, we assume that the surface data is mapped onto the unit sphere via an invertible spherical mapping of its associated cortical surface . We then use a hierarchical spherical registration (Lyu et al., 2019) as a core component of the proposed data augmentation. We extend this theory to a trajectory encoding. To update a spherical location, its spherical displacement is modeled by two successive rotations, and the composite rotation is encoded via spherical harmonics decomposition (Lyu et al., 2019). More formally, given an arbitrary global axis z, we define the tangent plane at z with two orthonormal bases u1 and u2. Let [·]× denote a 3-by-3 skew-symmetric matrix to represent a cross product. The two respective rotations R1 and R2 about and of z can be written as a matrix exponential
| (2) |
| (3) |
such that for , , ,
| (4) |
where expz(·) is the exponential map at . From Eqs. (2) and (3), the composite rotation is given by R = R2 · R1 as a function of (, , ω). For , a new location is determined by
| (5) |
This encodes any rotation of the special orthogonal group with the three parameters. As these parameters are global, the resulting rotation is rigid. The idea can be extended to spatially varying rotation (parameters). At for (θ, ϕ) ∈ [0, π] × [−π, π], let Yl,m (θ, ϕ) denote a real-valued spherical harmonics basis at degree l and order m, where and |m| ≤ l. By letting , spatially varying rotation (or its associated parameters) can be obtained by plugging a set of spherical harmonics coefficients and into Eq. (4):
| (6) |
Similarly, ω can be written as a function of spherical harmonics coefficients .
| (7) |
By finding optimal spherical harmonics coefficients, we can register two (or multiple) surfaces, and this can be efficiently solved via a gradient decent using the second order approximation (Lyu et al., 2019).
Key advantages of such encoding can be summarized as follows: (a) decomposable deformation trajectory: a local spherical displacement can be decomposed via spherical harmonics, and (b) single-run registration: extra registration steps are unnecessary to generate intermediate deformation at lower degrees thanks to orthonormality of spherical harmonics basis functions, which accelerates computation of the intermediate deformation. Using these characteristics, we can generate intermediate deformation of a given sample efficiently.
2.2.2. Feature deformation
To deform cortical folds for spherical data augmentation, we adapt the idea of spherical registration that locally alters spherical locations (Lyu et al., 2019). Specifically, we compute spherical harmonics coefficients after co-registration of spherical data (e.g., mean curvature). Cortical surfaces generally do not hold the same number of vertices, which hinders consistent handling of spherical data. To address this issue, many applications including Jiang et al. (2019) have re-tessellated input spheres via icosahedral subdivisions (Baumgardner and Frederickson, 1985) in a semi-uniform way. We re-tessellate spherical data in this manner to feed the deformed spheres to the networks (Jiang et al., 2019).
Formally, the deformed sphere at degree l is considered as a collection of new spherical locations . For , the updated location can be written by
| (8) |
where
| (9) |
We denote a cortical feature map (spherical data) at degree l by such that . Given a point q(θ, ϕ) of the icosahedral mesh, we determine a unique location (θ, ϕ) on . Therefore, a new feature map can be generated by
| (10) |
Thus, has the same number of vertices with a deformed feature map. In practice, the generation of new features is involved with an extensive triangle search over the triangular mesh. For computational efficiency, we use a customized axis-aligned bounding box (AABB) hierarchy, in which spherical locations are represented by spherical polar coordinates as proposed in Lyu et al. (2019).
2.2.3. Feature space approximation
We decompose deformation trajectories and collect all the deformed samples driven by their intermediate deformation to approximate the feature space from the deformed samples (i.e., per trajectory). Intuitively speaking, is a feature map that is rigidly aligned to that of a target surface (or template), i.e., global rotation. becomes non-rigid and closer to the target surface data as l increases. Specifically, we co-register every possible pair within training samples. Once again, our approach does not require multiple registration steps for every degree of spherical harmonics by using their orthonormality. Hence, we compute spherical harmonics coefficients once at the highest degree and reconstruct local displacements by controlling the number of basis functions. Note that the augmented samples do not change the original neuroanatomy (i.e., sulcal intersection/addition/removal) but instead enable local displacements (i.e., local translation/scaling constrained by ) via spherical registration without violating the spherical topology such as a sign change in surface normal (or triangle flip). Fig. 3 shows an example of pair-wise registration and their intermediate deformation that captures a deformation trajectory. We emphasize that spherical registration drives spherical data to be matched to that of a target sphere, whereas deformed annotation does not necessarily match that of the target; the use of just a singe training sample can insufficiently cover sulcal variability.
Fig. 3.
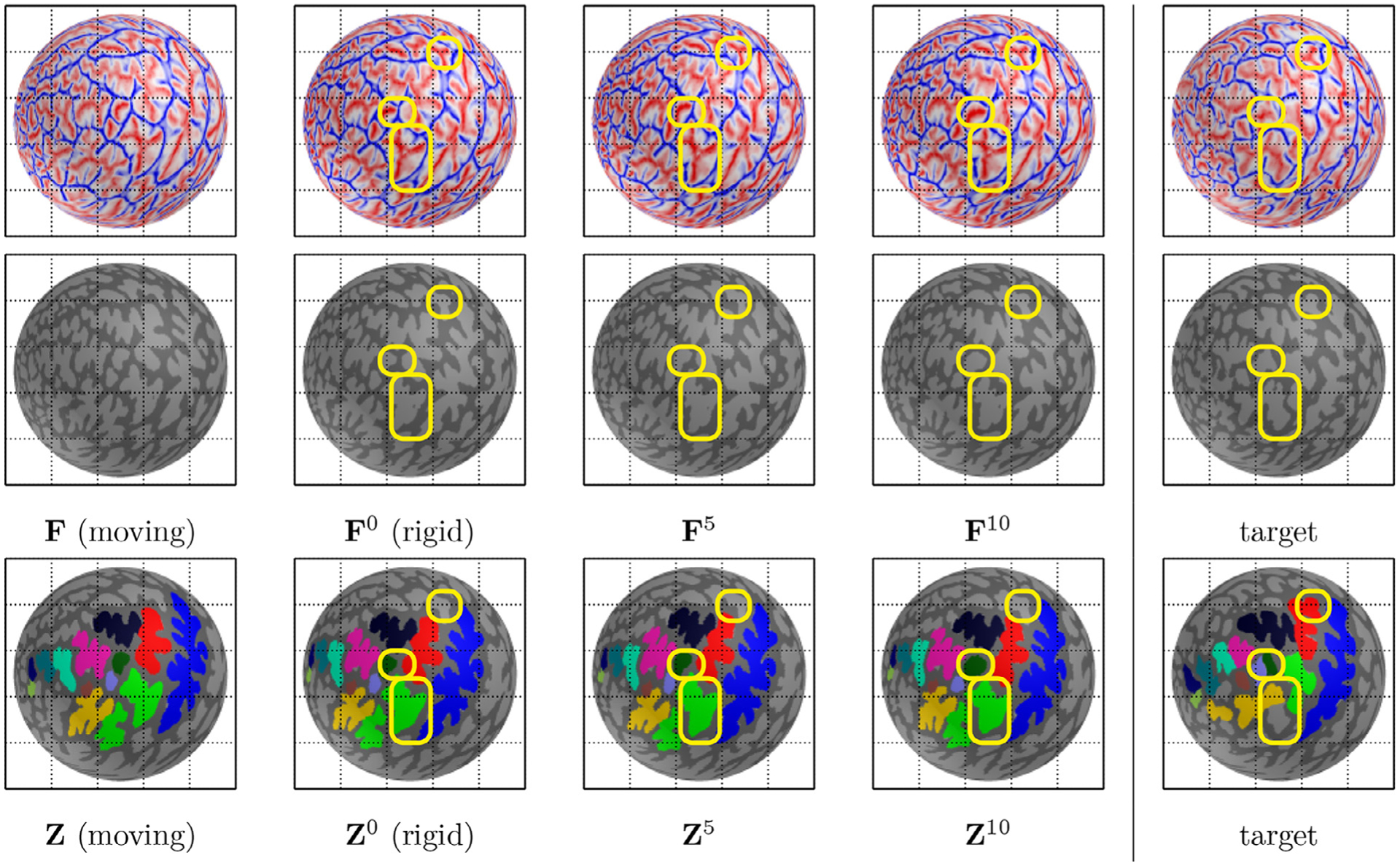
The proposed data augmentation. Top/Middle: input (binarized) spherical data (geometric feature) F is deformed to that of a target sphere. After rigid rotation (F0), the deformed spherical data become closer as a degree of spherical harmonics increases. Bottom: the manual annotation Z is driven by the intermediate deformation. Even with the improved geometric feature matching, manual annotation does not necessarily match due to spatial inconsistency and various sulcal branches (yellow box). This implies that a single training sample is insufficient to capture variability of sulci in LPFC. For data augmentation, the proposed method utilizes intermediate deformation of the combinatorial registration, by which sulcal variability can be better captured than a single training sample. Thus, model training is generalized by learning neuroanatomical variations provided by manual annotation for a set of similar spherical data (geometric features), to which the enhanced inference of unseen data belongs.
2.3. Context-aware training
As discussed earlier, the gestational timepoint, during which a sulcus emerges is directly related to their morphological prominence: primary sulci appear first and are largest/deepest, while tertiary sulci appear last and are smallest/shallowest (besides dimples; Armstrong et al. (1995); Chi et al. (1977); Sanides (1962, 1964); Welker (1990)). As we used these facts to help guide the order, in which we manually defined sulci in LPFC, we also use these facts to guide the context-aware training. We hence propose hierarchical training to mirror these associations rather than one-time learning of both primary/secondary and tertiary sulci together. As the true labels of primary and secondary sulci are unknown in unseen data, we infer spatial information of primary and secondary sulci from a trained model with only these labels as they are relatively stable as indicated in our LPFC work (Hao et al., 2020) and as motivated by context encoders for CNNs (Salehi et al., 2017; Xiang et al., 2017). We then feed the prior information (extra input channels) to the networks, which requires a two-stage training process. In particular, we tweak Eq. (1) to enable two-stage training. We formulate likelihoods of the 6 primary/secondary sulci and background as follows:
| (11) |
There must be overlap with the background label in the second stage of training for tertiary sulci. Thus, we let be a sub-collection of likelihoods that exclude . Note that we do not re-normalize as it can significantly boost a likelihood of one of the 6 sulci. The final likelihoods for a full set of the labels have the following form:
| (12) |
In the first training stage, we find optimal parameters of Eq. (11). Once trained, we draw likelihoods from fN to feed the second training of Eq. (12). We successively solve the respective likelihood functions of Eqs. (11) and (12) via the spherical CNNs proposed by Jiang et al. (2019). The readers are referred to the original methodology (theory, implementation, software, etc.) in Jiang et al. (2019) for details.
Since the likelihood map is computed over the icosahedral mesh, this needs to be mapped back to its associated cortical surface Ω to determine vertex-wise sulcal labels. For ∀v ∈ Ω at degree l, there exists a unique triangle of the icosahedral mesh that contains a spherical location of . By finding a barycentric coordinate from the closest triangle in the icosahedral mesh, we interpolate to assign a likelihood to v, say . We use the same AABB hierarchy as used in the icosahedral re-tessellation for an efficient triangle search.
2.4. Spatial coherence
CNN architectures tend to offer spatial coherence reasonably well (albeit, not perfectly) as convolutional layers cover local to global regions. In our application, maximum likelihood-based sulcal labeling often suffers from spatial incoherence although spatial coherence is implicitly encouraged in the spherical CNNs as shown in Fig. 4. Moreover, the boundaries of the sulcal regions are variable, which can yield several isolated connected components per sulcal label. To remove tiny isolated regions, we use a graph-cut technique proposed by Boykov and Kolmogorov (2004). The technique utilizes a min-cut/max-flow algorithm that minimizes an energy function encoded by the within- and between-cluster similarity. Thus, the resulting sulcal labels become smoother and more spatially coherent. Specifically, we construct a graph of Ω from its adjacent matrix M that defines neighborhood relationships of Ω. For ∀v ∈ Ω, we assign a negative log-likelihood given by
| (13) |
Cortical sulci tend to have a relatively small triangle size in the pial surface (Dale et al., 1999) as shown in Fig. 4. From this observation, we penalize spatial incoherence if two vertices are spatially close. Formally, the pair-wise relationship between neighborhood nodes is thus written by
| (14) |
where and M(v, v′) = 1. For v ∈ Ω, we can assign its initial label by finding the maximum likelihood from . We formulate the following energy function as a linear combination of the two terms in Eqs. (13) and (14) that can be optimized via a standard graph-cut technique (Boykov and Kolmogorov, 2004).
| (15) |
where , is a scaling factor, and I is an indicator function
| (16) |
The solution determines sulcal labels with their improved spatial coherence.
Fig. 4.

Improved spatial coherence. (a) cortical sulci tend to have a relatively small triangle size in the pial surface. (b) the maximum likelihood-based inference often yields isolated regions (yellow). (c) a standard graph-cut technique is used to refine spatial coherence. From the observation of adaptive triangle size in the pial surface, neighborhood relationship is encoded by the edge length. (d) the resulting labels become more spatially coherent to the manual annotation.
3. Experimentaldesign
3.1. Imaging data
3.1.1. Pediatriccohort
We randomly chose 60 individuals (27 female, 33 male, age range 6–18 years) from the Neurodevelopment of Reasoning Ability (NORA) study (Ferrer et al., 2013; Wendelken et al., 2017). All participants and their parents gave their informed assent or consent to participate in the study approved by the Committee for the Protection of Human Subjects at the University of California, Berkeley. Brain imaging data were collected on a Siemens 3T Trio system at the University of California Berkeley Brain Imaging Center. High-resolution T1-weighted MPRAGE anatomical scans (TR = 2,300 ms, TE = 2.98 ms, 1 × 1 × 1 mm3 voxel spacing) were acquired. All T1-weighted images were visually inspected for scanner artifacts. We used a standard FreeSurfer pipeline (v6.0) (Dale et al., 1999) to generate cortical surfaces, and each reconstruction was visually inspected for segmentation errors and subsequently corrected if any were found.
3.1.2. Adult cohort
We analyzed a subset of the multi-modal imaging data available for individual subjects from the Human Connectome Project (HCP) (Van Essen et al., 2012). We began with the first 5 numerically listed HCP subjects and then randomly selected 31 additional human subjects from the HCP for a total of 36 individuals (17 female, 19 male, age range 22–36 years). T1-weighted anatomical scans (. 8 ×. 8 ×. 8 mm3 voxel spacing) were acquired in native space from the HCP database, along with outputs from the HCP modified FreeSurfer pipeline (Glasser et al., 2013). The details on image acquisition parameters and image processing can be found in Glasser et al. (2013).
3.2. Manual sulcal labeling
Guided by a recent comprehensive proposal for labeling sulci in LPFC (Petrides, 2018; Petrides and Pandya, 2012), each sulcus was manually defined within each individual hemisphere on the inflated mesh. The curvature metric distinguished the boundaries between sulcal and gyral components, and manual lines were drawn to separate sulcal components based on the proposal by Petrides and colleagues (Petrides, 2018; Petrides and Pandya, 2012), as well as the appearance of sulci across the inflated, pial, and smoothed white matter surfaces (standard outputs of the FreeSurfer pipeline). We maintained the number of components for all sulci (e.g., the three components of the posterior middle frontal sulcus) based on the proposal. Manually labeling thousands of sulci is an arduous and time-consuming process. Considering the novel proposal of tertiary sulci in LPFC, and to prevent researchers from having to manually define sulci multiple times, we implemented a four-tiered, coarse-to-fine procedure motivated by our previous work (K.S.W) in ventral temporal cortex (Weiner, 2019; Weiner et al., 2014). First, screenshots of pial and inflated surfaces were taken for each subject and hemisphere. Second, independent raters (J.A.M., J.Y., and W.V.) coarsely labeled these sulci using text and drawing tools in the screenshots. Third, definitions were modified by a neuroanatomist (K.S.W.) and finalized among the four of us through discussions regarding any contentious definitions (the fine portion of the coarse-to-fine procedure). J.A.M., J.Y., and W.V. then defined the finalized versions of these sulci as further described in Miller et al. (2020b); Voorhies et al. (2020b). Thus, while inter-rater reliability is widely used to assess the consistency of neuroanatomical structures manually defined by experts, to expedite the labeling process, finalized manual definitions of sulci were conducted only once during the last stage of our four-tiered procedure. Consequently, we are unable to assess inter-rater reliability quantitatively at this time as label files were generated only once after the definitions of sulci were already agreed upon among the experts involved in the labeling procedure.
The following 13 sulci in LPFC were examined in this study: (1) the central sulcus, (2) the superior precentral sulcus, (3) the inferior precentral sulcus, (4) the anterior component of the superior frontal sulcus (sfs), (5) the posterior component of the sfs, (6) the inferior frontal sulcus, (7) the posterior component of the posterior middle frontal sulcus (pmfs), (8) the intermediate component of the pmfs, (9) the anterior component of the pmfs (Miller et al., 2020b; Petrides, 2018), (10) the horizontal component of the intermediate frontal sulcus (imfs), (11) the vertical component of the imfs, (12) the medial frontomarginal sulcus, and (13) the intermediate frontomarginal sulcus. Table 1 summarizes the sulci with their acronyms. We emphasize that while tertiary sulci are often not identifiable in every hemisphere in LPFC (Amiez et al., 2020; Garrison et al., 2015; Lopez-Persem et al., 2019; Petrides, 2018), the tertiary sulci examined here are identified in all 192 hemispheres that are included in the present study and in previous studies (Miller et al., 2020b; Voorhies et al., 2020b).
Table 1.
6 primary/secondary and 7 tertiary sulci.
| Acronym | Region | Acronym | Region | Acronym | Region |
|---|---|---|---|---|---|
| cs | central sulcus | sprs | superior precentral sulcus | iprs | inferior precentral sulcus |
| sfs_p | posterior component of the superior frontal sulcus | sfs_a | anterior component of the superior frontal sulcus | ifs | inferior frontal sulcus |
| pmfs_p | posterior component of the posterior middle frontal sulcus | pmfs_i | intermediate component of the posterior middle frontal sulcus | pmfs_a | anterior component of the posterior middle frontal sulcus |
| imfs_h | horizontal component of the intermediate frontal sulcus | imfs_v | vertical component of the intermediate frontal sulcus | ||
| mfms | medial frontomarginal sulcus | ifms | intermediate frontomarginal sulcus |
The labeling approach was the same between the two hemispheres. The labeling process started with the most stable sulci in the LPFC area of interest in the order in which they emerge in gestation according to previous work (Chi et al., 1977): (1) central sulcus (20–23 weeks) and precentral sulcus (sprs and iprs; 24 −27 weeks) posteriorly, (2) superior frontal sulci (sfs_a and sfs_p; 24–27 weeks) superiorly, and (3) inferior frontal sulcus inferiorly (28–31weeks). We then defined the two intermediate frontal sulci (imfs_h and imfs_v) followed by the medial (mfms) and intermediate (ifms) components of the frontomarginal sulcus. Finally, we defined the three components (pmfs_a, pmfs_p, and pmfs_i) of the posterior middle frontal sulcus. To our knowledge, exact gestational timestamps are unknown for these latter 7 sulci. For example, while Chi et al. (1977) documented that “tertiary superior, middle, and inferior frontal ” sulci emerge between 36–39 weeks in gestation, the explicit labeling of these 7 tertiary sulci in LPFC was not available during that time period and was proposed very recently by Petrides (2018); Petrides and Pandya (2012). Thus, due to the fact that the main morphological feature discriminating tertiary from primary/secondary sulci is depth and the morphology of tertiary sulci in LPFC are significantly more variable than primary/secondary sulci in LPFC (Miller and Cohen, 2001; Miller et al., 2020c; Voorhies et al., 2020b), we use (a) the timepoint in which the sulci emerge in gestation and (b) the variability in depth and surface area to discriminate tertiary from primary/secondary sulci in the present work. As illustrated in Fig. 1, primary/secondary sulci (cs, sfs_a, sfs_p, ifs, sprs, iprs) are in blue and what we consider as tertiary sulci for the present work are in red due to their extensive variability in depth and smaller surface area compared to the primary/secondary sulci.
While classic and modern (a handful of examples: Armstrong et al. (1995); Chi et al. (1977); Sanides (1962, 1964); Turner (1948); Vogt et al. (1995); Welker (1990)) and modern (a handful of examples: Amiez et al. (2020); Lopez-Persem et al. (2019); Mangin et al. (2004); Weiner (2019); Weiner and Zilles (2016)) studies acknowledge shallow “dimples ” on the cortical surface, these dimples are in addition to tertiary sulci and were often ascribed numbers or letters instead of an actual name in classic neuroanatomical work (Bonin and Bailey, 1951) because they were not identifiable consistently enough to warrant a name. In some cases, there was contention if a cortical indentation was a dimple or a tertiary sulcus. For example, while Retzius (1896) referred to the sulcus sagitallis gyri fusiformis, Bonin and Bailey (1951) more than 50 years later referred to this same indentation as dimple y (Weiner and Zilles, 2016). Thus, it remains an open question what the quantitative cutoff are for differentiating a tertiary sulcus from a dimple. Additionally, recent work (Amiez et al., 2020; Schall et al., 2020) proposes that consistent dimples in non-human primates deepen throughout evolution and become tertiary sulci in humans. For these reasons and because tertiary sulci in LPFC are quite prominent (~1.2 cm in depth and ~500 mm2 in surface area; Miller et al. (2020b)), we use the term tertiary sulci rather than dimples in this paper.
Altogether, the definitions of primary, secondary, and tertiary sulci are based on the timepoint in gestation during which the sulci emerge as recognized by classic and modern anatomists (Armstrong et al., 1995; Chi et al., 1977; Connolly, 1950; Cunningham, 1892; Miller et al., 2020b; 2020c; Retzius, 1896; Sanides, 1962; 1964; Turner, 1948; Weiner, 2019; Weiner et al., 2014; Weiner and Zilles, 2016; Welker, 1990). That is, primary sulci emerge first in gestation, are largest (in terms of surface area) and deepest, while tertiary sulci emerge last in gestation, are typically smallest, and also the shallowest, while secondary sulci are in between – historical details that we have discussed at length in a recent review of LPFC (Miller et al., 2020c). Nevertheless, we also acknowledge that determining which sulci are primary, secondary, or tertiary can be contentious. As such, we are not fully tied to these definitions and only emphasize that this is the first study to use surface data augmentation and context-aware training for spherical CNNs to define (i) subcomponents of the fms (mfms, ifms), (ii) subcomponents of the imfs (imfs_h, imfs_v), and (iii) subcomponents of the pmfs (pmfs_p, pmfs_i, and pmfs_a; Table 1). Despite contentions regarding sulcal definitions, we emphasize that the latter pmfs subcomponents are most assuredly tertiary sulci as they emerge last in gestation among sulci in LPFC (Chi et al., 1977; Cunningham, 1892; Miller et al., 2020a; Retzius, 1896; Turner, 1948) as well as are small and shallow compared to other sulci in LPFC (Miller et al., 2020b; 2020c; Petrides, 2018; Voorhies et al., 2020b) as also shown in Fig. 1.
3.3. Dataaugmentation
For surface data, we used three geometric features (N = 3): mean curvature of the inflated cortical surface, average convexity (Dale et al., 1999), and mean curvature of the smoothed white matter surface. Note that we did not alter the original cortical surfaces (mesh) for the data augmentation. The geometric features were generated from the exact same surfaces as used for the manual labeling. In spherical registration (Fischl et al., 1999a; Lyu et al., 2019; Yeo et al., 2010), these three features have shown to effectively capture details of cortical geometry in a multi-resolution manner. As feature deformation was marginal after a degree of 10 in our data, we used a degree of 10 in the spherical harmonics decomposition. After co-registration, we incrementally added the estimated spherical harmonics coefficients up to l = 10 to augment samples along the deformation trajectories. Note that we excluded any pair of co-registration that belonged to a validation/test set. In the surface registration, it took about 2 mins on a single CPU thread to estimate spherical harmonics coefficients at an icosahedral level of 6 (40,962 vertices) and 5 sec to generate 11 deformed features via spherical harmonics reconstruction (on average) on a single thread.
3.4. Training and label refinement
To train the spherical CNNs, we used 10,242 vertices via icosahedral subdivision at level of 5 with an entry feature layer with size of 32. A standard Adam optimizer (Kingma and Ba, 2014) was employed over categorical cross-entropy loss with a learning rate of .01. We employed temperature scaling (Guo et al., 2017) to alleviate over-confident inference during the optimization. For all the experiments, we used 5-fold cross validation with 60% for training and 20% each for validation and test by rotating the partitions. For each fold, we fixed the weights of the trained model when the validation set reached the lowest validation loss. We then summarized labeling performance on each test set after the cross validation. The training at each fold is therefore not necessarily optimized for the test set. We trained each hemisphere with the same experimental configurations on both pediatric and adult cohorts. The overall computation was performed on an Intel Xeon Silver 4114 processor and an NVIDIA Titan Xp with 12Gb memory. Finally, we used λ = 1 in the graph-cut technique.
Note that the improvement of Dice overlap was marginal (less than .01 for all methods) between before and after the graph-cut technique as shown in Table 2, while qualitatively improved spatial coherence is observed in both primary/secondary and tertiary sulci by removing tiny isolated regions as shown in Fig. 4. For a learning rate in training of the neural networks, there is no systematic adjustment proposed yet in present studies to the best of our knowledge, so tuning of such a hyperparameter (learning rate) still remains challenging in deep neural networks. From our observations, learning rate of .01 offers balanced training between computational speed and stability in its convergence compared to .1 or .001.
Table 2.
Average improved Dice overlap between before and after the graph-cut technique. Quantitatively, the overall performance gain in Dice overlap after the graph-cut technique is marginal, while qualitatively, small isolated clusters are removed as shown in Fig. 4, which improves spatial coherence.
| Pediatric | Adult | |||
|---|---|---|---|---|
| Left | Right | Left | Right | |
| Multi-atlas | .0097 | .0007 | .0066 | .0007 |
| Naive | .0076 | .0008 | .0008 | .0076 |
| Rotation | .0015 | .0017 | .0011 | .0046 |
| Non-rigid | .0016 | .0057 | .0004 | .0046 |
| Non-rigid+Context | .0030 | .0037 | .0002 | .0049 |
3.5. Baseline methods
Due to the absence of existing methods that support the annotation protocol of tertiary sulci defined in this work, we used three generic baseline methods for comparison: a conventional multi-atlas approach using majority voting (Hansen and Salamon, 1990; Kittler, 1998) and the original spherical CNNs (Jiang et al., 2019) with/without rotation data augmentation, in which we computed an optimal rigid alignment for every pair within the training samples to allow (rigid) positional variations of each individual sample. In the multi-atlas approach, we employed leave-one-out cross validation to maximize its performance, where all subjects (template) are registered to a target subject and the most frequent inferences are used to determine the final labels (majority voting). For the spherical CNNs, we preserved the same parameters for training configurations including the (i) hyperparameter settings, (ii) model architectures, (iii) exact partitions of cross-fold validation, and (iv) spatial coherence for post-processing except for the number of input channels. For all methods, we rigidly aligned each individual subject to a single target to avoid potential performance degeneration by data misalignment.
4. Results
4.1. Surface data augmentation
In the pediatric cohort, we performed a single paired t-test on the average Dice overlap (60 left (right) hemispheres) and 13 multiple paired t-tests for all sulci (60 left (right) hemispheres per region) over each baseline method. For the average Dice overlap evaluation (single paired t-test), the proposed data augmentation achieves significantly higher Dice overlap for both primary/secondary and tertiary sulci than multi-atlas and conventional training without rotation data augmentation as summarized in Table 3. Although no significant improvement is observed in primary/secondary sulci compared to rotation data augmentation, the proposed data augmentation shows improved Dice overlap for tertiary sulci (see Table 3). In region-wise analysis (13 multiple paired t-tests), the proposed augmentation yields significantly improved Dice overlap in the left (right) hemisphere for 12 (12) and 9 (10) out of 13 sulci compared to the multi-atlas approach and the conventional training without rotation data augmentation after multi-comparison correction for the 13 sulci by false discovery rate (FDR; Benjamini and Hochberg (1995)) at q = .05 (see Table 3). Note that a full set of subjects except for one to be labeled was used in the multi-atlas approach, which may already have an advantage over other methods in terms of capturing sample variations despite its moderate performance. We did not find regional differences (based on statistical significance) compared to the conventional training with rotation data augmentation except for the central sulcus in the right hemisphere (Fig. 6). Importantly, performance (in terms of Dice overlap) is not worse with the proposed data augmentation than the other methods (Fig. 6).
Table 3.
Summary of average Dice overlap (mean ± stdev.) for the pediatric and adult cohorts. Legend: significant improvement (p < .05) for Non-rigid+Context* (blue) compared to the baseline methods; significant improvement for Non-rigid or Non-rigid+Context* (black) compared to the baseline methods.
| Cohort | Hemisphere | Approach | Overall | Primary/secondary | Tertiary |
|---|---|---|---|---|---|
| Pediatric | Left | Multi-atlas | .4528±.0585* | .6610±.0614* | .2744±.0871* |
| Naive | .5296±.0921* | .6989±.0832* | .3844±.1327* | ||
| Rotation | .5718±.1054* | .7595±.0820 | .4110±.1611* | ||
| Non-rigid | .5944±.1117 | .7649±.0816 | .4482±.1733 | ||
| Non-rigid+Context | .6159±.0956 | .7650±.0810 | .4880±.1529 | ||
| Right | Multi-atlas | .4348±.0674* | .6375±.1041* | .2611±.0783* | |
| Naive | .5156±.0916* | .6895±.1019* | .3665±.1312* | ||
| Rotation | .5742±.1102* | .7355±.1267* | .4360±.1565* | ||
| Non-rigid | .5908±.1241 | .7478±.1319 | .4562±.1667 | ||
| Non-rigid+Context | .6076±.1189 | .7574±.1256 | .4791±.1672 | ||
| Adult | Left | Multi-atlas | .4843±.0647* | .6521±.0679* | .3404±.0890* |
| Naive | .4227±.1012* | .5778±.1206* | .2897±.1051* | ||
| Rotation | .5712±.0968* | .7185±.0798* | .4450±.1387* | ||
| Non-rigid | .6046±.1131 | .7449±.0930 | .4843±.1588 | ||
| Non-rigid+Context | .6333±.0928 | .7471±.0922 | .5357±.1351 | ||
| Right | Multi-atlas | .4703±.0695* | .6450±.0738* | .3205±.1113* | |
| Naive | .4136±.1141* | .6034±.1559* | .2508±.1165* | ||
| Rotation | .5544±.1049* | .7460±.0808* | .3901±.1696* | ||
| Non-rigid | .5893±.1033 | .7508±.0973 | .4508±.1808 | ||
| Non-rigid+Context | .6067±.0984 | .7654±.0879 | .4707±.1566 |
Fig. 6.
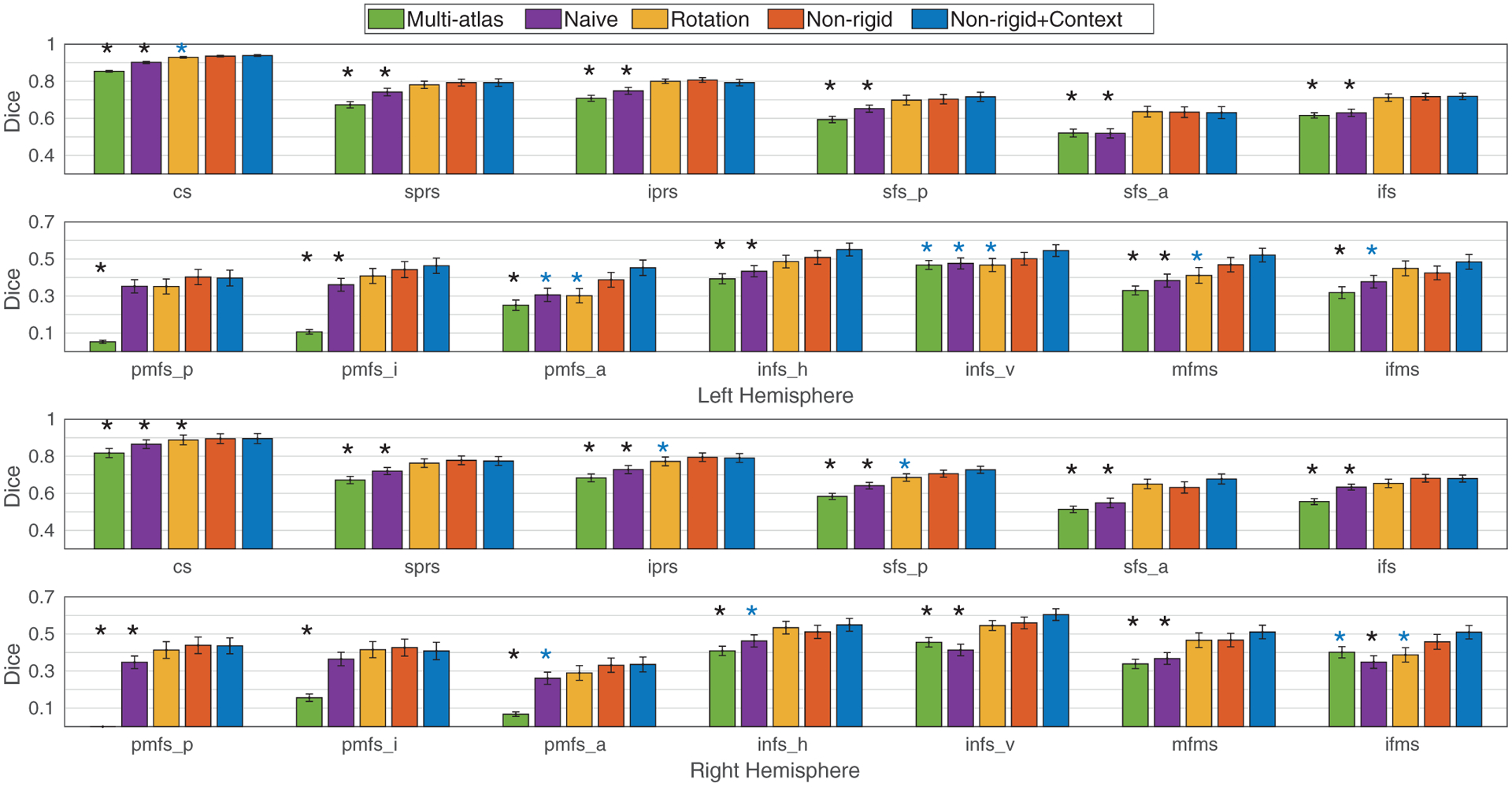
Dice overlap per sulcus in the pediatric cohort in LPFC. The statistical significance is reported after multi-comparison correction among the 13 sulci (FDR at q= .05). The proposed data augmentation (Non-rigid) shows higher accuracy (Dice overlap) than the baseline methods. After the context-aware training, the Dice overlap is further improved in primary/secondary (cs (left hemisphere); iprs and sfs_p (right hemisphere)) and tertiary (pmfs_a, imfs_v, and mfms (left hemisphere); ifms (right hemisphere)) sulci compared to the conventional training with rotation data augmentation. Importantly, the proposed method does not perform worse than the baseline methods for any sulcus. Legend: standard errors (hat); significant improvement compared to the baseline methods for Non-rigid+Context* (blue); for Non-rigid or Non-rigid+Context* (black).
Similar to the pediatric cohort, we performed a single paired t-test on the average Dice overlap (36 left (right) hemispheres) and 13 multiple paired t-tests for all sulci (36 left (right) hemispheres per region) compared to the baseline methods in the adult cohort. In the average Dice overlap (single paired t-test), the proposed data augmentation offers higher Dice overlap for both primary/secondary and tertiary sulci in the adult cohort than multi-atlas and conventional training without rotation data augmentation as summarized in Table 3. The proposed data augmentation also offers improved Dice overlap for tertiary sulci compared to rotation data augmentation (Fig. 7). Despite this improvement in the definition of tertiary sulci, no improvement is observed in either hemisphere for the definition of primary/secondary sulci using the proposed data augmentation (Table 3). Importantly, in region-wise analysis (13 multiple paired t-tests), we found that the proposed method yields significantly improved Dice overlap in the left (right) hemisphere in 10 (10) and 13 (13) out of 13 sulci compared to the multi-atlas approach and the conventional training without rotation data augmentation (FDR at q = .05; Fig. 7). We did not find significant region-wise differences in both primary/secondary and tertiary sulci from the conventional training with rotation data augmentation in the region-wise analysis (Fig. 7) despite overall improvement across all of the tertiary sulci in the average Dice overlap evaluation (Table 3).
Fig. 7.
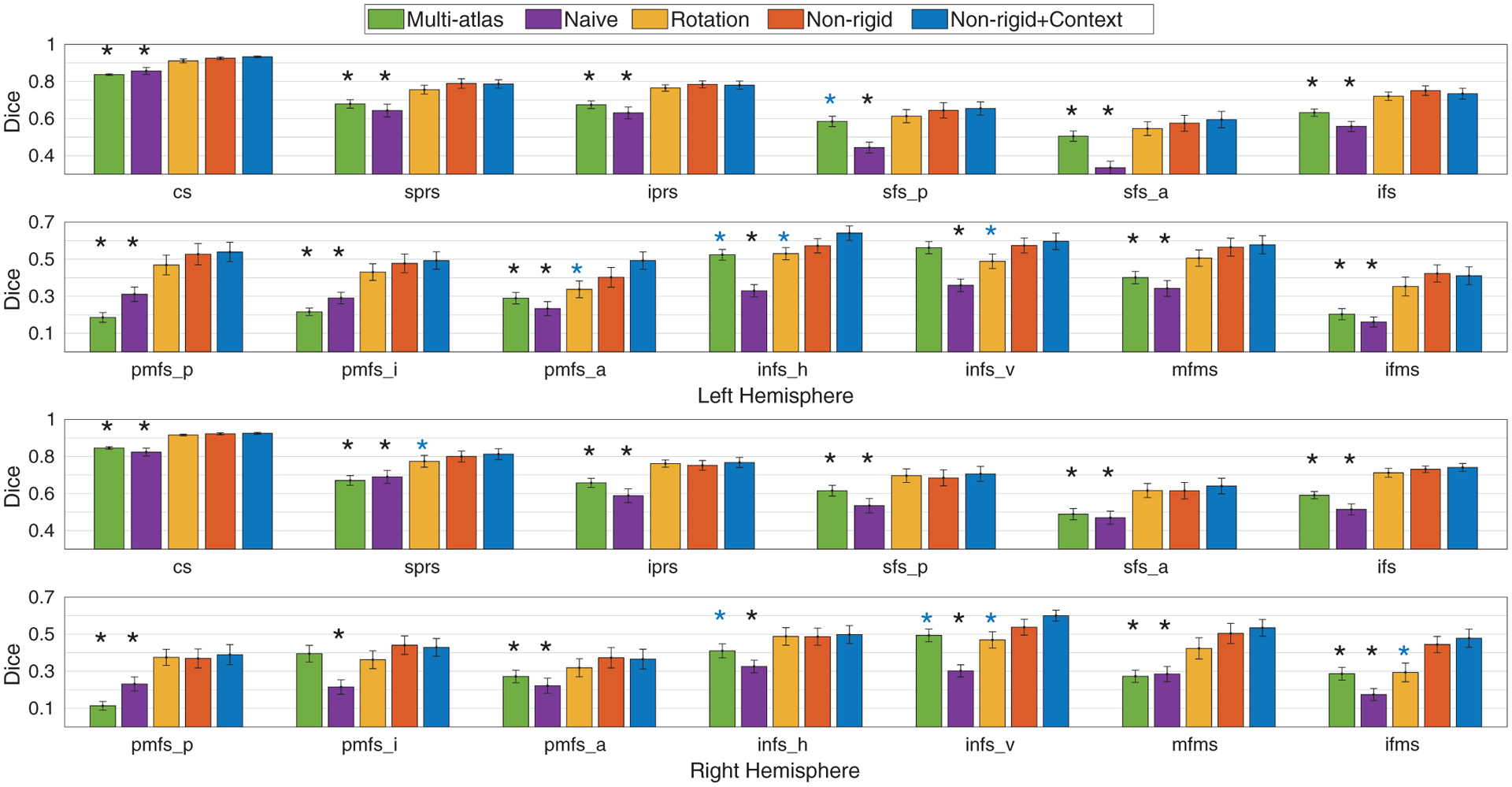
Dice overlap per sulcus in the adult cohort in LPFC. The statistical significance is reported after multi-comparison correction among the 13 sulci (FDR at q= .05). The proposed data augmentation shows higher accuracy (Dice overlap) than the baseline methods. After the context-aware training, the Dice overlap is further improved in primary/secondary (sprs (right hemisphere)) and tertiary (pmfs_a, imfs_h, and imfs_v (left hemisphere); imfs_v and ifms (right hemisphere)) sulci compared to the conventional training with rotation data augmentation. Importantly, the proposed method does not perform worse compared to the baseline methods for any sulcus. Legend: standard errors (hat); significant improvement than the baseline methods for Non-rigid+Context* (blue); for Non-rigid or Non-rigid+Context* (black).
4.2. Context-awaresulcal labeling
We trained the spherical CNNs with 6 primary/secondary sulci with the same configurations as used in other baseline methods (Hansen and Salamon, 1990; Jiang et al., 2019; Kittler, 1998). In average Dice overlap evaluations (single paired t-test), the proposed context-aware training provides significantly improved Dice overlap particularly for tertiary sulci over the baselines on both pediatric and adult cohorts (see Table 3). In region-wise analysis (13 multiple t-tests), as the spherical CNNs were trained with 6 primary/secondary sulci in the first place, a handful of these sulci show significant improvement in both hemispheres after the context-aware training, while we observed significant improvement in Dice overlap in several tertiary sulci (see Figs. 6 and 7) in both pediatric and adult cohorts after multi-comparison correction over the 13 sulci by FDR at q = .05.
When considering the average Dice overlap, two-sample t-tests (60 versus 36 hemispheres) reveal comparable Dice overlap in both hemispheres between the pediatric and adult cohorts in the proposed method and the baseline methods including multi-atlas and rotation data augmentation (p >. 05). Additionally, the spherical CNNs without data augmentation achieve significantly different accuracy between the two cohorts; i.e., Table 3 shows absolute difference of about.1 in Dice overlap for overall, primary/secondary sulci, and tertiary sulci (p < .005). Notably, the context-aware training even with a small sample size (adult cohort) still offers a high Dice overlap comparable to that in the pediatric cohort.
To investigate the effect of the context-aware training over the proposed data augmentation, we compared the proposed data augmentation without and with the context-aware training. In the average Dice evaluation, one-sample t-tests reveal improved performance overall and for tertiary sulcal labels in the left (right) hemisphere in the pediatric cohort (p = .0244 (.0444) and p = .0103 (.0761)) and in the adult cohort (p = .0128 (.0397) and p = .0035 (.1277)). In the region-wise analysis, however, there are no significant differences without and with the context-aware training in either cohort after multi-comparison correction across the 13 sulci (FDR at q = .05).
5. Discussion
Here, we tested if spherical data augmentation methods and context-aware training improved the automatic identification of deep primary and secondary sulci as well as shallow tertiary sulci in LPFC. Leveraging a rich dataset of 13 manually defined sulci in LPFC in children, adolescents, and adults spanning in age between 5 and 35, our present findings show that spherical data augmentation and context-aware training successfully label sulci in LPFC (even shallow tertiary sulci) automatically with improved performances beyond the leave-one-out multi-atlas approach and spherical CNNs without/with conventional rotation data augmentation. The proposed context-aware training further improved the identification of tertiary sulci while achieving comparable overall accuracy in both pediatric and adult cohorts (Figs. 6 and 7). As the proposed data augmentation is generic, our method can be utilized in genus-zero surface-based studies that suffer from the scarcity of the training samples in addition to sulcal labeling. In the remainder of this section, we discuss these findings (i) in the context of surface data augmentation, (ii) relative to context-aware training, and (iii) the automatic labeling of tertiary sulci, which together aim to provide structural and functional understanding of LPFC.
5.1. Surface data augmentation
Our results indicate that data augmentation is key to improve labeling performance of sulci in LPFC, particularly with small sample sizes. Even with simple rotation data augmentation, there was noticeable improvement in both pediatric and adult cohorts included in the present study (Table 3; Figs. 5–7). By extending simple rotation to non-rigid deformation trajectories, the proposed data augmentation further improved overall performance compared to the conventional data augmentation. This suggests that the intermediate non-rigid deformation is likely to fill a gap of augmented features generated by simple rotation data augmentation, which consequently improves the model generalizability. Meanwhile, the proposed data augmentation yielded comparable Dice overlap between the pediatric and adult cohorts despite a relatively small size of data in the adult cohort (N = 36). In addition to the brain maturation in the adult cohort, it is likely that even small training samples already have sufficient variations after the proposed data augmentation to capture primary sulci, which might not be fully captured in rotation data augmentation. By contrast, the conventional spherical CNNs without data augmentation show significant performance degeneration (Figs. 5–7). This implies that the conventional training without data augmentation is limited to account for sulcal variability.
Fig. 5.
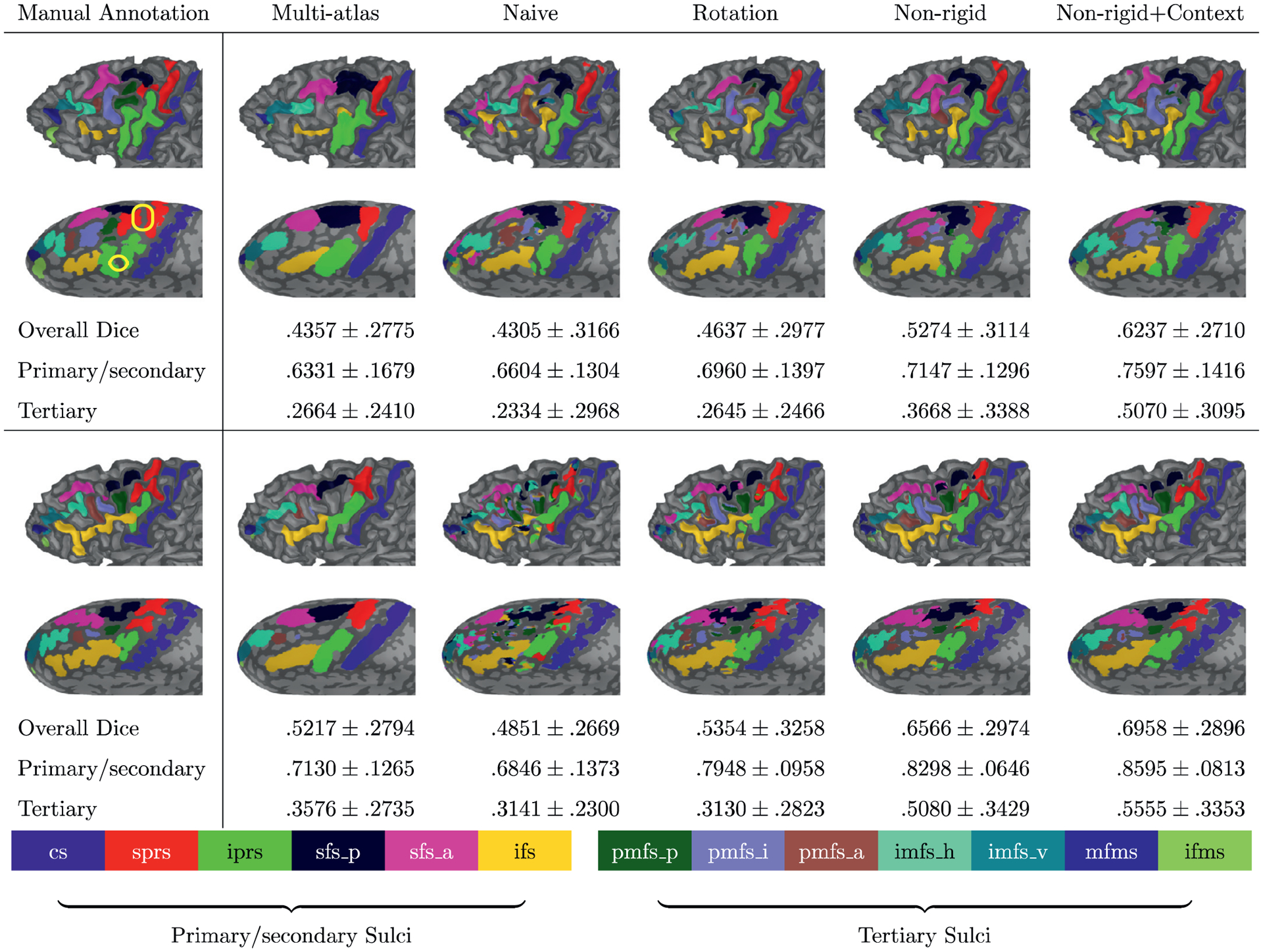
Visual inspection of label inference on example subjects around the average performance (top: pediatric sample, bottom: adult sample). The multi-atlas approach (second column from left) lacks geometric details of labeled regions along cortical folds as indicated by the rather low dice coefficient compared to the rightmost column. The conventional training without data augmentation (third column from left: Naive) shows poor performance that generates small isolated segments even after improving spatial coherence due to limited generalizability particularly with a small sample size. Although rotation data augmentation (fourth column from left) offers higher accuracy than the conventional training, the inference is more improved (generalized) with the proposed data augmentation, and the labeling accuracy of tertiary sulci can be further improved by introducing context information (two rightmost columns: Non-rigid and Non-rigid+Context). Note that there is even considerable variability in sulci that emerge relatively early in gestation such as sprs and iprs. In the pediatric example (top left), the reader can appreciate the annectant gyral components (plis de passage; Gratiolet (1854); Mangin et al. (2019); Parent (2014); yellow box) between both iprs and sprs.
From a technical perspective, there could be multiple choices in implementing a feature space that embeds surface deformation trajectories. In our earlier work (Hao et al., 2020; Parvathaneni et al., 2019a), we co-registered all training samples together in a group-wise manner, in which the training samples were registered to their group mean while the mean is refined during the registration. Since the augmented samples become closer to their group mean, it is likely that the labeling accuracy increases if unseen data is similar to the group mean; i.e., this strategy can improve the variability of the group mean. This approach is beneficial with computational efficiency and compact representation for relatively consistent samples. In the present work, we instead co-registered every possible pair of training samples. Although it is hard to determine what is best among these approaches depending on data variations, the group mean could be less effective in general unless unseen data is registered to it, and the trained models could be consequently biased toward common sulcal patterns estimated from the registration. On the other hand, despite the computational demand of the co-registration and model training, the combinatorial co-registration covers a smooth transition across samples, which can thus enhance the model generalizability.
The proposed data augmentation may not sufficiently cover certain samples that contain cortical patterns too far from those of the training set. This is a general issue in modern deep neural networks regardless of data augmentation. Our work rather focuses on how training performance can be improved from a fixed (limited) set of training samples. We hypothesized that unseen data will be likely covered by the proposed data augmentation if their (partial) folding patterns are a subset of generated intermediate patterns guided by surface registration. In our experiments, we showed that non-rigid deformation offers better performance in terms of Dice overlap than the baseline methods. Yet, the proposed data augmentation is based on the decomposable deformation driven by surface geometry, which may not necessarily enforce neuroanatomical alignment as shown in Fig. 3. A potential direction to address such an issue would be explicit matching of labeled sulcal regions (e.g., sulcal curves) used in previous work such as Auzias et al. (2013); Choi et al. (2015); Datar et al. (2013); Glaunès et al. (2004); Lyu et al. (2015); Van Essen (2005). To utilize these methods, however, a tractable feature space (e.g., decomposable deformation) needs to be carefully designed for efficient augmentation of surface data.
The surface registration used in this work offers a diffeomorphic mapping in a discrete domain as discussed in Lyu et al. (2019). Briefly, the method uses spatially varying rotation based on spherical harmonics, so it is differentiable (spherical harmonics consist of trigonometric functions) and invertible (a transpose of the rotation matrix). It also holds a one-to-one correspondence on a discretized surface (triangular mesh) by preventing triangle flips (self-intersection) at every optimization step that adjusts the update step size associated with spherical harmonics coefficients. The augmented data samples hold diffeomorphism (invertible deformation without self-intersection). In this way, anatomical deformation obeys a smooth transition between training samples, which guarantees that the augmented data is uniquely determined on a re-tessellated surface mesh; i.e., no changes of the original neuroanatomy and thus, a preservation of spatial coherence of the sulcal labels. Although random local deformation may more efficiently generalize the trained models in terms of a wider data variation, diffeomorphism is not guaranteed by random perturbation on spherical harmonics coefficients in the current approach, which, in turn, may not produce valid deformation of the cortical surfaces. Further investigation into more generalized data augmentation will likely increase the model generalizability.
Modern surface reconstruction pipelines (Cointepas et al., 2001; Dale et al., 1999; Kim et al., 2005) enforce a reconstructed cortical surface to be genus-zero, by which a cortical surface can be simplified while preserving its topology. Hence, a spherical mapping offers a common parametric space that allows easy manipulation of highly convoluted cortical surface data. Although mapping distortions always exist, the influence of these distortions can be reduced via conformal or area-preserving mappings (Fischl et al., 1999a; Gu et al., 2004; Haker et al., 2000; Quicken et al., 2000; Tosun et al., 2004). We also found that the spherical mapping (Fischl et al., 1999b) used in this work preserves surface areas well; the average absolute difference of the whole sulci across the 96 subjects is 112.17 ± 20.40 mm2 (116. 81 ± 19. 92 mm2), which is equivalent to. 1202 ± .0180 % (.1247 ± .0183 %) of the total surface area in the left (right) hemisphere (see supplementary information for the region-wise differences). As discussed previously, little work is present in surface data augmentation as this requires the encoding of surface deformation into a tractable feature space as well as efficient computation to draw samples from that space. Although non-parametrization-based surface registration is appealing such as particle shape correspondence (Datar et al., 2013; Oguz et al., 2009) or spectral alignment (Gahm et al., 2018; Lombaert et al., 2013; Wright et al., 2015), these methods would need explicit encoding of deformation trajectories in the context of surface data augmentation, which can be explored in future work.
5.2. Context-aware training
The proposed context-aware training offers improved Dice overlap even above and beyond the proposed data augmentation. In particular, we observed significantly improved performance on several tertiary sulci in both cohorts over rotation data augmentation (see Figs. 6 and 7), whereas the spherical CNNs with only the proposed data augmentation do not outperform rotation data augmentation on these individual sulci despite overall improved Dice overlap. In the proposed context-aware training, the variability in tertiary sulci is taken into account by including primary/secondary sulci as a priori, which improves the Dice overlap of tertiary sulci. This suggests that the relatively consistent spatial information of primary/secondary sulci can improve the automatic definition of tertiary sulci with surface data augmentation and context-aware training. We note that this improvement is specific to tertiary sulci as primary/secondary sulci are less variable than tertiary sulci and as such, context-aware training provided no significant improvement over data augmentation (see Figs. 6 and 7). Future studies can test if these findings are specific to LPFC or also extend to primary/secondary and tertiary sulci in other portions of cortex.
Despite the improved average Dice overlap for tertiary sulci both without and with the proposed context-aware training, no region-wise statistical difference was observed. As reported in previous studies (Barkovich, 2005; Blanton et al., 2001; Chi et al., 1977; Miller et al., 2020b; Sanides, 1962; 1964), tertiary sulci in LPFC appear last in gestation and continue to develop after birth, while primary sulcal regions are largely developed prenatally (Encha-Razavi and Sonigo, 2003; Raybaud et al., 2003; Rodriguez-Carranza et al., 2008). Hence, a small sample size might be sufficient to capture neuroanatomical variability in primary/secondary sulci. On the other hand, the high neuroanatomical variability in LPFC tertiary sulci might not be fully learned by the proposed context-aware training given the relatively limited training samples in the present study despite the improved global performance. We expect that increasing the sample size will improve the model generalizability as well as boost performance in the ability to predict tertiary sulci, which can be tested in future research.
Based on our previous (Hao et al., 2020) and present findings, there are likely remaining inaccuracies in the automated definition of primary and secondary sulci. Nevertheless, these inaccuracies will be regularized through the introduction of a priori information as additional input channels together with tertiary sulci as well as their geometry. As such, the proposed training approach does not solely depend on the prior information from the first stage of the training (i.e., the inference of primary/secondary sulci). We also acknowledge that the proposed method can be biased toward more heavily weighting the larger, more prominent sulci. Such an imbalanced issue has been studied in Lin et al. (2017), in which CNNs are likely to pay more attention to larger sulci. This imbalance could be alleviated in future studies by incorporating other features such as focal loss (Lin et al., 2017) to avoid over-emphasizing large, prominent sulci during training. Adjustments based on sulcal variability (or prediction accuracy) would also be a suitable alternative to address imbalances in the present sulcal labeling protocol.
We used mean curvature and average convexity for input channels. Mean curvature of the inflated surfaces captures global folding patterns of their associated cortical surfaces with simplified neuroanatomical details as shown in Fig. 2. This measure guides a global alignment of the cortical surfaces, and each individual measure provides a different level of details that can support a global-to-local representation of the cortical surfaces as shown in several surface registration methods (Fischl et al., 1999a; Lyu et al., 2019; Yeo et al., 2010). The learning process could be further improved with other cortical measures such as shape index (Koenderink, 1990) or various metrics (Batchelor et al., 2002; Kim et al., 2016) because they are capable of offering complementary measures of local geometry from different perspectives.
Finally, a small portion of cortical surface area was labeled and used to train the spherical CNNs. Nevertheless, this does not suggest that training is based only on geometry within these labeled regions. The unlabeled regions are capable of informing how neuroanatomical structures are positioned as convolutional layers cover local to global regions. In turn, the networks are likely to attend to their neighborhood as well as other cortical lobes rather than only labeled regions. Future studies can come closer to determining which neuroanatomical information (e.g. individual sulci/gyri, lobes, etc.) contribute most to the automated definition of sulci in LPFC.
5.3. Labeling performance
The present approach advances recent work aiming to develop machine learning techniques to define sulci throughout cortex (Borne et al., 2020; Cointepas et al., 2001; Joshi et al., 2012; Lyu et al., 2010; Mangin et al., 1995; Parvathaneni et al., 2019b; Perrot et al., 2008; Rettmann et al., 2002; Riviere et al., 2002; Sandor and Leahy, 1997; Shattuck et al., 2009; Shi et al., 2009; Tao et al., 2002; Tu et al., 2007; Yun et al., 2019). Specifically, by focusing on fine-grained, manual sulcal definitions in LPFC, the present study included additional sulcal regions in LPFC that were combined together as one sulcus in previous studies (Borne et al., 2020; Cointepas et al., 2001). For example, while the previous work considered one intermediate frontal sulcus (imfs), the present approach broke this down into five distinct sulcal components (imfs_v, imfs_h, pmfs_a, pmfs_i, and pmfs_p) as recently proposed in post-mortem brains by Petrides (2018) akin to component-wise sulcal pattern analysis (Régis et al., 2005), which was recently verified in-vivo in pediatric (Voorhies et al., 2020b; Yao et al., 2020) and adult cohorts (Miller et al., 2020b). These previous studies can use the present approach to guide the definition of tertiary sulci in LPFC.
As a given sulcus often intersects, or shares a sulcal bed, with other nearby sulci due to extensive individual differences in these intersections, there are often unclear regional boundaries. Since tertiary sulci are small in their surface area and shallow in their depth as shown in Fig. 1, these intersections often make it particularly difficult to determine regional boundaries. In turn, unclear boundaries are likely to interchangeably improve/degenerate Dice overlap in a cortical expanse with intersecting tertiary sulci. A component-wise analysis (or graphical representation) of individual sulci would be promising to handle such heterogeneous anatomical structures (Le Goualher et al., 1999; Mangin et al., 1995; Shi et al., 2009). Yet, this approach needs a careful design of sub-structures that encode fine-grained tertiary sulci defined in the present sulcal labeling protocol. In our study, although such a problem is handled by relying solely on cortical geometry including likelihood estimation and spatial coherence refinement, this could be more effectively addressed by incorporating detailed anatomical associations in future work. Our proposed data augmentation with context-aware training did not improve the automated identification of all sulci, and performance was lower for tertiary than primary/secondary sulci. Nevertheless, performance for tertiary sulci can be significantly improved by considering combined tertiary sulcal complexes: i) posterior middle frontal sulcus (a combination of the pmfs_p, pmfs_i, and pmfs_a), the intermediate frontal sulcus (a combination of the imfs_h and imfs_v), and the frontomarginal sulcus (a combination of mfms and ifms); see Figs. 6 and 7 for performance of individual sulci and supplementary information for combined tertiary sulci. For example, when considering all 3 pmfs components together, performance approaches a Dice overlap of.7 in the left hemisphere for both cohorts (Fig. S.1 in supplementary information). Thus, future studies could use these tools to accurately identify these tertiary sulcal “complexes ” automatically and then manually define each component from these automated definitions.
Finally, automatically identifying tertiary sulci in future studies will also likely reveal novel neuroanatomical-functional links in LPFC and in other cortical expanses. For instance, recent findings indicate that tertiary sulci serve as mesoscale links between microstructural and functional properties in LPFC (Miller et al., 2020b) and also predict reasoning skills in children (Voorhies et al., 2020b). The main limitation of this previous work is that tertiary sulci must be manually defined in order to uncover these links, which requires neuroanatomical expertise that most human brain mappers do not have. The present tools will now allow neuroimaging researchers to identify tertiary sulci with much less manual intervention. Nevertheless, manual intervention will still be necessary as labeling performance is much lower for tertiary than primary/secondary sulci (Figs. 6 and 7). A main goal of future studies will be to improve labeling performance in order to minimize the manual intervention in labeling tertiary sulci. As recent studies also show local morphological differences in tertiary sulci between typical controls and different clinical populations (Brun et al., 2016; Garrison et al., 2015; Parker et al., 2020), these future improvements will be especially critical for uncovering the role of tertiary sulcal morphology in health and disease. Finally, as previous studies also show that tertiary sulci in other parts of cortex are also functionally (Lopez-Persem et al., 2019; Weiner et al., 2014) and behaviorally (Amiez et al., 2018; Garrison et al., 2015) meaningful, these tools will also improve understanding regarding the relationship among neuroanatomical structure, functional representations, and behavior in other portions of cortex in future studies.
6. Conclusion
We presented registration-based spherical data augmentation with context-aware training for the automated labeling of sulci in LPFC in pediatric and adult cohorts. To augment training samples, we defined a feature space represented by surface deformation trajectories, over which augmented features were drawn along their trajectories. Specifically, we decomposed the trajectories via spherical harmonics for smooth feature sampling as well as computational efficiency. Motivated by context encoders, we also employed biological associations of sulci in the proposed two-stage training. The experimental results in both pediatric and adult cohorts showed that our approach improved the Dice overlap particularly in 7 tertiary sulci in LPFC over the leave-one-out multi-atlas approach and the spherical CNNs without/with conventional rotation data augmentation. The proposed context-aware training further improved inference in tertiary sulci while achieving comparable overall accuracy in both cohorts. Finally, as the proposed data augmentation is generic, our method can be utilized in genus-zero surface-based studies that suffer from a scarcity of training samples in addition to sulcal labeling in future studies.
Supplementary Material
Funding
This work was supported in part by the National Institute of Health (NIH) under Grant R01EB017230, R01MH102246, R21HD100858, and K24MH110598, NCRR Grant UL1 RR024975-01, and NCATS Grant 2 UL1 TR000445-06, in part by the National Science Foundation (NSF) under CAREER IIS1452485 in part by VISE/VICTR under VR3029, in part by the Vanderbilt Data Science Institute Summer Research Program, and in part by the NVIDIA GPU Grant Program.
Data used in this paper were partly provided by the Neurodevelopment of Reasoning Ability study funded by NIH under NINDS R01NS057156 and NSF under BCS1558585.
Data used in this paper were partly provided by the Human Connectome Project, WU-Minn Consortium (Principal Investigators: David Van Essen and Kamil Ugurbil; 1U54MH091657) funded by the 16 NIH Institutes and Centers that support the NIH Blueprint for Neuroscience Research; and by the McDonnell Center for Systems Neuroscience at Washington University.
Footnotes
Declaration of competing interest
The authors declare no conflict of interest.
Supplementary material
Supplementary material associated with this article can be found, in the online version, at 10.1016/j.neuroimage.2021.117758.
Association cortices are considered portions of the cerebral cortex that develop late in gestation (compared to primary sensory cortices) and that also show a protracted development after birth (Armstrong et al., 1995; Chi et al., 1977; Miller et al., 2020b; 2020c; Voorhies et al., 2020b; Weiner, 2019; Welker, 1990). It is widely accepted that association cortices are more structurally and functionally variable than primary sensory cortices. As shallow, tertiary sulci are more likely to be located in association cortices (Armstrong et al., 1995; Chi et al., 1977; Welker, 1990), their identification and morphology also reflect this increased variability (Fig. 1).
References
- Amiez C, Sallet J, Hopkins WD, Meguerditchian A, Hadj-Bouziane F, Hamed SB, Wilson CR, Procyk E, Petrides M, 2020. Author correction: Sulcal organization in the medial frontal cortex provides insights into primate brain evolution. Nat. Commun 11 (1), 1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amiez C, Wilson CR, Procyk E, 2018. Variations of cingulate sulcal organization and link with cognitive performance. Sci. Rep 8 (1), 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Armstrong E, Schleicher A, Omran H, Curtis M, Zilles K, 1995. The ontogeny of human gyrification. Cereb. Cortex 5 (1), 56–63. [DOI] [PubMed] [Google Scholar]
- Asman AJ, Landman BA, 2014. Hierarchical performance estimation in the statistical label fusion framework. Med. Image Anal 18 (7), 1070–1081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Auzias G, Lefevre J, Le Troter A, Fischer C, Perrot M, Régis J, Coulon O, 2013. Model-driven harmonic parameterization of the cortical surface: Hip-hop. IEEE Trans. Med. Imaging 32 (5), 873–887. [DOI] [PubMed] [Google Scholar]
- Barkovich AJ, 2005. Pediatric Neuroimaging Lippincott Williams & Wilkins. [Google Scholar]
- Batchelor PG, Smith AC, Hill DLG, Hawkes DJ, Cox TCS, Dean A, 2002. Measures of folding applied to the development of the human fetal brain. IEEE Trans. Med. Imaging 21 (8), 953–965. [DOI] [PubMed] [Google Scholar]
- Baumgardner JR, Frederickson PO, 1985. Icosahedral discretization of the two-sphere. SIAM J. Numer. Anal 22 (6), 1107–1115. [Google Scholar]
- Benjamini Y, Hochberg Y, 1995. Controlling the false discovery rate: a practical and powerful approach to multiple testing. J. R. Stat. Soc. Ser. B (Methodological) 289–300. [Google Scholar]
- Blanton RE, Levitt JG, Thompson PM, Narr KL, Capetillo-Cunliffe L, Nobel A, Singerman JD, McCracken JT, Toga AW, 2001. Mapping cortical asymmetry and complexity patterns in normal children. Psychiatry Res. Neuroimaging 107 (1), 29–43. [DOI] [PubMed] [Google Scholar]
- Bonin G. v., Bailey P, 1951. The isocortex of man
- Borne L, Rivière D, Mancip M, Mangin J-F, 2020. Automatic labeling of cortical sulci using patch-or cnn-based segmentation techniques combined with bottom-up geometric constraints. Med. Image Anal 101651. [DOI] [PubMed] [Google Scholar]
- Boykov Y, Kolmogorov V, 2004. An experimental comparison of min-cut/max-flow algorithms for energy minimization in vision. IEEE Trans. Pattern Anal. Mach. Intell 26 (9), 1124–1137. [DOI] [PubMed] [Google Scholar]
- Brun L, Auzias G, Viellard M, Villeneuve N, Girard N, Poinso F, Da Fonseca D, Deruelle C, 2016. Localized misfolding within brocas area as a distinctive feature of autistic disorder. Biol. Psychiatry: Cognit. Neurosci. Neuroimaging 1 (2), 160–168. [DOI] [PubMed] [Google Scholar]
- Cachia A, Paillère-Martinot M-L, Galinowski A, Januel D, de Beaurepaire R, Bellivier F, Artiges E, Andoh J, Bartrés-Faz D, Duchesnay E, et al. , 2008. Cortical folding abnormalities in schizophrenia patients with resistant auditory hallucinations. Neuroimage 39 (3), 927–935. [DOI] [PubMed] [Google Scholar]
- Chi JG, Dooling EC, Gilles FH, 1977. Gyral development of the human brain. Ann. Neurol 1 (1), 86–93. [DOI] [PubMed] [Google Scholar]
- Choi PT, Lam KC, Lui LM, 2015. Flash: Fast landmark aligned spherical harmonic parameterization for genus-0 closed brain surfaces. SIAM J. Imaging Sci 8 (1), 67–94. [Google Scholar]
- Cohen TS, Geiger M, Köhler J, Welling M, 2018. Spherical cnns. In: Proceedings og the International Conference on Learning Representations. [Google Scholar]
- Cointepas Y, Mangin J-F, Garnero L, Poline J-B, Benali H, 2001. Brainvisa: software platform for visualization and analysis of multi-modality brain data. Neuroimage 13 (6), 98. [Google Scholar]
- Connolly CJ, 1950. External Morphology of the Primate Brain CC Thomas. [Google Scholar]
- Cunningham DJ, 1892. Contribution to the Surface Anatomy of the Cerebral Hemispheres Academy House. [Google Scholar]
- Dale AM, Fischl B, Sereno MI, 1999. Cortical surface-based analysis: I. segmentation and surface reconstruction. Neuroimage 9 (2), 179–194. [DOI] [PubMed] [Google Scholar]
- Datar M, Lyu I, Kim S, Cates J, Styner MA, Whitaker R, 2013. Geodesic distances to landmarks for dense correspondence on ensembles of complex shapes. In: Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer, pp. 19–26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Winter F-L, Zhu Q, Van den Stock J, Nelissen K, Peeters R, de Gelder B, Vanduffel W, Vandenbulcke M, 2015. Lateralization for dynamic facial expressions in human superior temporal sulcus. NeuroImage 106, 340–352. [DOI] [PubMed] [Google Scholar]
- Encha-Razavi F, Sonigo P, 2003. Features of the developing brain. Child’s Nervous Syst 19 (7–8), 426–428. [DOI] [PubMed] [Google Scholar]
- Esteves C, Allen-Blanchette C, Makadia A, Daniilidis K, 2018. Learning so(3) equivariant representations with spherical cnns. In: Proceedings of the European Conference on Computer Vision. [Google Scholar]
- Ferrer E, Whitaker KJ, Steele JS, Green CT, Wendelken C, Bunge SA, 2013. White matter maturation supports the development of reasoning ability through its influence on processing speed. Dev. Sci 16 (6), 941–951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl B, Sereno M, Tootell R, Dale A, 1999. High-resolution intersubject averaging and a coordinate system for the cortical surface. Hum. Brain Mapp 8 (4), 272–284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl B, Sereno MI, Dale AM, 1999. Cortical surface-based analysis: Ii: inflation, flattening, and a surface-based coordinate system. Neuroimage 9 (2), 195–207. [DOI] [PubMed] [Google Scholar]
- Gahm JK, Shi Y, Initiative ADN, et al. , 2018. Riemannian metric optimization on surfaces (rmos) for intrinsic brain mapping in the laplace–beltrami embedding space. Med. Image Anal 46, 189–201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garrison JR, Fernyhough C, McCarthy-Jones S, Haggard M, Simons JS, 2015. Paracingulate sulcus morphology is associated with hallucinations in the human brain. Nat. Commun 6 (1), 1–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glasser MF, Sotiropoulos SN, Wilson JA, Coalson TS, Fischl B, Andersson JL, Xu J, Jbabdi S, Webster M, Polimeni JR, et al. , 2013. The minimal preprocessing pipelines for the human connectome project. Neuroimage 80, 105–124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glaunès J, Vaillant M, Miller MI, 2004. Landmark matching via large deformation diffeomorphisms on the sphere. J. Math. Imaging Vis 20 (1–2), 179–200. [Google Scholar]
- Gratiolet L, 1854. On the folding of cortical folding of the human and primates brain Paris: Bertrand (Fre). [Google Scholar]
- Gu X, Wang Y, Chan TF, Thompson PM, Yau S-T, 2004. Genus zero surface conformal mapping and its application to brain surface mapping. IEEE Trans. Med. Imaging 23 (8), 949–958. [DOI] [PubMed] [Google Scholar]
- Gu Z, Cheng J, Fu H, Zhou K, Hao H, Zhao Y, Zhang T, Gao S, Liu J, 2019. Ce-net: Context encoder network for 2d medical image segmentation. IEEE Trans. Med. Imaging 38 (10), 2281–2292. [DOI] [PubMed] [Google Scholar]
- Guo C, Pleiss G, Sun Y, Weinberger KQ, 2017. On calibration of modern neural networks. In: Proceedings of the 34th International Conference on Machine Learning-Volume 70, pp. 1321–1330. [Google Scholar]
- Haker S, Angenent S, Tannenbaum A, Kikinis R, Sapiro G, Halle M, 2000. Conformal surface parameterization for texture mapping. IEEE Trans. Visual. Comput. Graphics 6 (2), 181–189. [Google Scholar]
- Hansen LK, Salamon P, 1990. Neural network ensembles. IEEE Trans. Pattern Anal. Mach. Intell 12 (10), 993–1001. [Google Scholar]
- Hao L, Bao S, Tang Y, Gao R, Parvathaneni P, Miller JA, Voorhies W, Yao J, Bunge SA, Weiner KS, Landman BA, Lyu I, 2020. Automatic labeling of cortical sulci using spherical convolutional neural networks in a developmental cohort. In: Proceedings of the IEEE 17th International Symposium on Biomedical Imaging (ISBI), pp. 412–415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hauberg S, Freifeld O, Larsen ABL, Fisher J, Hansen L, 2016. Dreaming more data: Class-dependent distributions over diffeomorphisms for learned data augmentation. In: Proceedings of the Artificial Intelligence and Statistics, pp. 342–350. [Google Scholar]
- Huang S-G, Lyu I, Qiu A, Chung MK, 2020. Fast polynomial approximation of heat kernel convolution on manifolds and its application to brain sulcal and gyral graph pattern analysis. IEEE Trans. Med. Imaging 39 (6), 2201–2212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang CM, Huang J, Kashinath K, Prabhat, Marcus P, Niessner M, 2019. Spherical CNNs on unstructured grids. In: Proceedings of the International Conference on Learning Representations. [Google Scholar]
- Joshi AA, Shattuck DW, Leahy RM, 2012. A method for automated cortical surface registration and labeling. In: Proceedings of the International Workshop on Biomedical Image Registration. Springer, pp. 180–189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim J, Singh V, Lee J, Lerch J, Ad-Dab’bagh Y, MacDonald D, Lee J, Kim S, Evans A, 2005. Automated 3-d extraction and evaluation of the inner and outer cortical surfaces using a Laplacian map and partial volume effect classification. NeuroImage 27 (1), 210–221. [DOI] [PubMed] [Google Scholar]
- Kim M, Wu G, Li W, Wang L, Son Y-D, Cho Z-H, Shen D, 2013. Automatic hippocampus segmentation of 7.0 tesla mr images by combining multiple atlases and auto-context models. NeuroImage 83, 335–345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim SH, Lyu I, Fonov VS, Vachet C, Hazlett HC, Smith RG, Piven J, Dager SR, Mckinstry RC, Pruett JR, et al. , 2016. Development of cortical shape in the human brain from 6 to 24months of age via a novel measure of shape complexity. NeuroImage 135, 163–176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kingma DP, Ba J, 2014. Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980 [Google Scholar]
- Kittler J, 1998. Combining classifiers: A theoretical framework. Pattern Anal. Appl 1 (1), 18–27. [Google Scholar]
- Koenderink JJ, 1990. Solid Shape MIT Press, Cambridge, MA, USA. [Google Scholar]
- Kondor R, Lin Z, Trivedi S, 2018. Clebsch–gordan nets: a fully fourier space spherical convolutional neural network. In: Proceedings of the Advances in Neural Information Processing Systems, pp. 10117–10126. [Google Scholar]
- Kondor R, Trivedi S, 2018. On the generalization of equivariance and convolution in neural networks to the action of compact groups. In: Proceedings of the International Conference on Machine Learning, pp. 2747–2755. [Google Scholar]
- Le Goualher G, Procyk E, Collins DL, Venugopal R, Barillot C, Evans AC, 1999. Automated extraction and variability analysis of sulcal neuroanatomy. IEEE Trans. Med. Imaging 18 (3), 206–217. [DOI] [PubMed] [Google Scholar]
- Lin T-Y, Goyal P, Girshick R, He K, Dollár P, 2017. Focal loss for dense object detection. In: Proceedings of the IEEE International Conference on Computer Vision, pp. 2980–2988. [Google Scholar]
- Lombaert H, Sporring J, Siddiqi K, 2013. Diffeomorphic spectral matching of cortical surfaces. In: Proceedings of the Information Processing in Medical Imaging. Springer, pp. 376–389. [DOI] [PubMed] [Google Scholar]
- Lopez-Persem A, Verhagen L, Amiez C, Petrides M, Sallet J, 2019. The human ventromedial prefrontal cortex: sulcal morphology and its influence on functional organization. J. Neurosci 39 (19), 3627–3639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lyu I, Kang H, Woodward ND, Styner MA, Landman BA, 2019. Hierarchical spherical deformation for cortical surface registration. Med. Image Anal 57, 72–88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lyu I, Kim S, Seong J, Yoo S, Evans A, Shi Y, Sanchez M, Niethammer M, Styner M, 2015. Robust estimation of group-wise cortical correspondence with an application to macaque and human neuroimaging studies. Front. Neurosci 9, 210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lyu I, Kim SH, Girault JB, Gilmore JH, Styner MA, 2018. A cortical shape-adaptive approach to local gyrification index. Med. Image Anal 48, 244–258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lyu I, Kim SH, Woodward ND, Styner MA, Landman BA, 2018. TRACE: A topological graph representation for automatic sulcal curve extraction. IEEE Trans. Med. Imaging 37 (7), 1653–1663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lyu I, Seong J, Shin S, Im K, Roh J, Kim M, Kim G, Kim J, Evans A, Na D, Lee J, 2010. Spectral-based automatic labeling and refining of human cortical sulcal curves using expert-provided examples. NeuroImage 52 (1), 142–157. [DOI] [PubMed] [Google Scholar]
- Mangin J, Riviere D, Cachia A, Duchesnay E, Cointepas Y, Papadopoulos-Orfanos D, Scifo P, Ochiai T, Brunelle F, Régis J, 2004. A framework to study the cortical folding patterns. NeuroImage 23, S129–S138. [DOI] [PubMed] [Google Scholar]
- Mangin J-F, Le Guen Y, Labra N, Grigis A, Frouin V, Guevara M, Fischer C, Rivière D, Hopkins WD, Régis J, et al. , 2019. plis de passage deserve a role in models of the cortical folding process. Brain Topogr 1–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mangin J-F, Régis J, Bloch I, Frouin V, Samson Y, López-Krahe J, 1995. A mrf based random graph modelling the human cortical topography. In: Proceedings of the Computer Vision, Virtual Reality and Robotics in Medicine. Springer, pp. 177–183. [Google Scholar]
- Miller EK, Cohen JD, 2001. An integrative theory of prefrontal cortex function. Annu. Rev. Neurosci 24 (1), 167–202. [DOI] [PubMed] [Google Scholar]
- Miller J, D’Esposito M, Weiner K, 2020a. Using tertiary sulci to map the cognitive globe of prefrontal cortex. PsyArXiv preprint doi: 10.31234/osf.io/y8f4b.. [DOI] [PubMed] [Google Scholar]
- Miller JA, Voorhies WI, Lurie DJ, D’Esposito M, Weiner KS, 2020b. A new sulcal landmark identifying anatomical and functional gradients in human lateral prefrontal cortex. bioRxiv 10.1101/2020.03.24.006577 [DOI] [Google Scholar]
- Miller JA, Voorhies WI, Lurie DJ, DEsposito M, Weiner KS, 2020c. Overlooked tertiary sulci serve as a meso-scale link between microstructural and functional properties of human lateral prefrontal cortex. bioRxiv [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nalepa J, Mrukwa G, Piechaczek S, Lorenzo PR, Marcinkiewicz M, Bobek–Billewicz B, Wawrzyniak P, Ulrych P, Szymanek J, Cwiek M, et al. , 2019. Data augmentation via image registration. In: Proceedings of the IEEE International Conference on Image Processing (ICIP). IEEE, pp. 4250–4254. [Google Scholar]
- Oguz I, Niethammer M, Cates J, Whitaker R, Fletcher T, Vachet C, Styner M, 2009. Cortical correspondence with probabilistic fiber connectivity. In: Prince J, Pham D, Myers K (Eds.), Information Processing in Medical Imaging 2009 Springer, Heidelberg, pp. 651–663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ono M, Kubik S, Abernathey CD, 1990. Atlas of the cerebral sulci Tps. [Google Scholar]
- Parent A, 2014. Louis pierre gratiolet (1815–1865) and his contribution to the study of cerebral convolutions in primates. Neurosci. Med 2014. [Google Scholar]
- Parker BJ, Voorhies W, Gomez J, Jiahui G, Furl N, Garrido L, Duchaine B, Weiner KS, 2020. On the role of tertiary sulci in developmental prosopagnosia. The FASEB J 34 (S1), 1. [Google Scholar]
- Parvathaneni P, Bao S, Nath V, Woodward ND, Claassen DO, Cascio CJ, Zald DH, Huo Y, Landman BA, Lyu I, 2019. Cortical surface parcellation using spherical convolutional neural networks. In: Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer, pp. 501–509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parvathaneni P, Nath V, McHugo M, Huo Y, Resnick SM, Woodward ND, Landman BA, Lyu I, 2019. Improving human cortical sulcal curve labeling in large scale cross-sectional mri using deep neural networks. J. Neurosci. Methods 324, 108311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perraudin N, Defferrard M, Kacprzak T, Sgier R, 2019. Deepsphere: Efficient spherical convolutional neural network with healpix sampling for cosmological applications. Astron. Comput 27, 130–146. [Google Scholar]
- Perrot M, Riviere D, Mangin J-F, 2008. Identifying cortical sulci from localization, shape and local organization. In: Proceedings of the 5th IEEE International Symposium on Biomedical Imaging: From Nano to Macro. IEEE, pp. 420–423. [Google Scholar]
- Petrides M, 2018. Atlas of the Morphology of the Human Cerebral Cortex on the Average MNI Brain Academic Press. [Google Scholar]
- Petrides M, Pandya DN, 2012. The frontal cortex. In: The Human Nervous System Elsevier, pp. 988–1011. [Google Scholar]
- Quicken M, Brechbuhler C, Hug J, Blattmann H, Székely G, 2000. Parameterization of closed surfaces for parametric surface description. In: Proceedings IEEE Conference on Computer Vision and Pattern Recognition. CVPR 2000 (Cat. No. PR00662), 1. IEEE, pp. 354–360. [Google Scholar]
- Raybaud C, Levrier O, Brunel H, Girard N, Farnarier P, 2003. Mr imaging of fetal brain malformations. Child’s Nervous Syst 19 (7–8), 455–470. [DOI] [PubMed] [Google Scholar]
- Régis J, Mangin J-F, Ochiai T, Frouin V, Riviére D, Cachia A, Tamura M, Samson Y, 2005. sulcal root generic model: a hypothesis to overcome the variability of the human cortex folding patterns. Neurologia medico-chirurgica 45 (1), 1–17. [DOI] [PubMed] [Google Scholar]
- Rettmann ME, Han X, Xu C, Prince JL, 2002. Automated sulcal segmentation using watersheds on the cortical surface. NeuroImage 15 (2), 329–344. [DOI] [PubMed] [Google Scholar]
- Retzius G, 1896. Das Menschenhirn: Studien in der Makroskopischen Morphologie Königlich Buchdruckerei. [Google Scholar]
- Riviere D, Mangin J-F, Papadopoulos-Orfanos D, Martinez J-M, Frouin V, Régis J, 2002. Automatic recognition of cortical sulci of the human brain using a congregation of neural networks. Med. Image Anal 6 (2), 77–92. [DOI] [PubMed] [Google Scholar]
- Rodriguez-Carranza CE, Mukherjee P, Vigneron D, Barkovich J, Studholme C, 2008. A framework for in vivo quantification of regional brain folding in premature neonates. Neuroimage 41 (2), 462–478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salehi SSM, Erdogmus D, Gholipour A, 2017. Auto-context convolutional neural network (auto-net) for brain extraction in magnetic resonance imaging. IEEE Trans. Med. Imaging 36 (11), 2319–2330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sandor S, Leahy R, 1997. Surface-based labeling of cortical anatomy using a deformable atlas. IEEE Trans. Med. Imaging 16 (1), 41–54. [DOI] [PubMed] [Google Scholar]
- Sanides F, 1962. Architectonics of the human frontal lobe of the brain. with a demonstration of the principles of its formation as a reflection of phylogenetic differentiation of the cerebral cortex. Monographien aus dem Gesamtgebiete der Neurologie und Psychiatrie 98, 1. [PubMed] [Google Scholar]
- Sanides F, 1964. Structure and function of the human frontal lobe. Neuropsychologia 2 (3), 209–219. [Google Scholar]
- Schall JD, Zinke W, Cosman J, Schall M, Paré M, Pouget P, 2020. On the evolution of the frontal eye field: Comparisons of monkeys, apes, and humans. In: Evolutionary Neuroscience Elsevier, pp. 861–890. [Google Scholar]
- Schwarzkopf DS, Rees G, 2013. Subjective size perception depends on central visual cortical magnification in human v1. PloS one 8 (3), e60550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seong S-B, Pae C, Park H-J, 2018. Geometric convolutional neural network for analyzing surface-based neuroimaging data. Front. Neuroinform 12, 42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shattuck DW, Joshi AA, Pantazis D, Kan E, Dutton RA, Sowell ER, Thompson PM, Toga AW, Leahy RM, 2009. Semi-automated method for delineation of landmarks on models of the cerebral cortex. J. Neurosci. Methods 178 (2), 385–392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi Y, Tu Z, Reiss AL, Dutton RA, Lee AD, Galaburda AM, Dinov I, Thompson PM, Toga AW, 2009. Joint sulcal detection on cortical surfaces with graphical models and boosted priors. IEEE Trans. Med. Imaging 28 (3), 361–373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shorten C, Khoshgoftaar TM, 2019. A survey on image data augmentation for deep learning. J. Big Data 6 (1), 60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tao X, Prince JL, Davatzikos C, 2002. Using a statistical shape model to extract sulcal curves on the outer cortex of the human brain. IEEE Trans. Med. Imaging 21 (5), 513–524. [DOI] [PubMed] [Google Scholar]
- Tosun D, Rettmann ME, Prince JL, 2004. Mapping techniques for aligning sulci across multiple brains. Med. Image Anal 8 (3), 295–309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tu Z, Bai X, 2009. Auto-context and its application to high-level vision tasks and 3d brain image segmentation. IEEE Trans. Pattern Anal. Mach. intelligence 32 (10), 1744–1757. [DOI] [PubMed] [Google Scholar]
- Tu Z, Zheng S, Yuille AL, Reiss AL, Dutton RA, Lee AD, Galaburda AM, Dinov I, Thompson PM, Toga AW, 2007. Automated extraction of the cortical sulci based on a supervised learning approach. IEEE Trans. Med. Imaging 26 (4), 541–552. [DOI] [PubMed] [Google Scholar]
- Turner OA, 1948. Growth and development of the cerebral cortical pattern in man. Archives of Neurology & Psychiatry 59 (1), 1–12. [DOI] [PubMed] [Google Scholar]
- Uzunova H, Wilms M, Handels H, Ehrhardt J, 2017. Training cnns for image registration from few samples with model-based data augmentation. In: Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer, pp. 223–231. [Google Scholar]
- Van Essen DC, 2005. A population-average, landmark-and surface-based (pals) atlas of human cerebral cortex. Neuroimage 28 (3), 635–662. [DOI] [PubMed] [Google Scholar]
- Van Essen DC, Ugurbil K, Auerbach E, Barch D, Behrens T, Bucholz R, Chang A, Chen L, Corbetta M, Curtiss SW, et al. , 2012. The human connectome project: a data acquisition perspective. Neuroimage 62 (4), 2222–2231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vogt BA, Nimchinsky EA, Vogt LJ, Hof PR, 1995. Human cingulate cortex: surface features, flat maps, and cytoarchitecture. J. Compar. Neurol 359 (3), 490–506. [DOI] [PubMed] [Google Scholar]
- Voorhies WI, Miller JA, Yao J, Bunge SA, Weiner KS, 2020. Cognitive insights from evolutionarily new brain structures in prefrontal cortex. bioRxiv [Google Scholar]
- Voorhies WI, Miller JA, Yao J, Raghuram I, Bunge SA, Weiner KS, 2020. Sulcal morphology of the lateral prefrontal cortex predicts individual differences in cognitive development. The FASEB J 34 (S1), 1. doi: 10.1096/fasebj.2020.34.s1.02670. [DOI] [Google Scholar]
- Weiner KS, 2019. The mid-fusiform sulcus (sulcus sagittalis gyri fusiformis). The Anatomical Record 302 (9), 1491–1503. [DOI] [PubMed] [Google Scholar]
- Weiner KS, Golarai G, Caspers J, Chuapoco MR, Mohlberg H, Zilles K, Amunts K, Grill-Spector K, 2014. The mid-fusiform sulcus: a landmark identifying both cytoarchitectonic and functional divisions of human ventral temporal cortex. Neuroimage 84, 453–465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weiner KS, Zilles K, 2016. The anatomical and functional specialization of the fusiform gyrus. Neuropsychologia 83, 48–62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Welker W, 1990. Why does cerebral cortex fissure and fold? In: Cerebral Cortex Springer, pp. 3–136. [Google Scholar]
- Wendelken C, Ferrer E, Ghetti S, Bailey SK, Cutting L, Bunge SA, 2017. Frontoparietal structural connectivity in childhood predicts development of functional connectivity and reasoning ability: A large-scale longitudinal investigation. J. Neurosci 37 (35), 8549–8558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilms M, Handels H, Ehrhardt J, 2017. Multi-resolution multi-object statistical shape models based on the locality assumption. Med. Image Anal 38, 17–29. [DOI] [PubMed] [Google Scholar]
- Wright R, Makropoulos A, Kyriakopoulou V, Patkee PA, Koch LM, Ruther-ford MA, Hajnal JV, Rueckert D, Aljabar P, 2015. Construction of a fetal spatio-temporal cortical surface atlas from in utero mri: Application of spectral surface matching. NeuroImage 120, 467–480. [DOI] [PubMed] [Google Scholar]
- Xiang L, Qiao Y, Nie D, An L, Lin W, Wang Q, Shen D, 2017. Deep auto-context convolutional neural networks for standard-dose pet image estimation from low-dose pet/mri. Neurocomputing 267, 406–416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yao J, Voorhies W, Miller J, Bunge S, Weiner K, 2020. Sulcal depth in lateral prefrontal cortex predicts working memory in childhood. The FASEB J 34 (S1), 1. doi: 10.1096/fasebj.2020.34.s1.04640. [DOI] [Google Scholar]
- Yeo B, Sabuncu M, Vercauteren T, Ayache N, Fischl B, Golland P, 2010. Spherical demons: Fast diffeomorphic landmark-free surface registration. IEEE Trans. Med. Imaging 29 (3), 650–668. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yun HJ, Chung AW, Vasung L, Yang E, Tarui T, Rollins CK, Ortinau CM, Grant PE, Im K, 2019. Automatic labeling of cortical sulci for the human fetal brain based on spatio-temporal information of gyrification. NeuroImage 188, 473–482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao A, Balakrishnan G, Durand F, Guttag JV, Dalca AV, 2019. Data augmentation using learned transformations for one-shot medical image segmentation. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 8543–8553. [Google Scholar]
- Zilles K, Armstrong E, Schleicher A, Kretschmann H-J, 1988. The human pattern of gyrification in the cerebral cortex. Anatomy Embryol 179 (2), 173–179. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


