A seasonal model to assess intervention strategies for preventing periodic recurrence of Lassa fever

Abstract

Lassa haemorrhagic fever is listed in WHO's Blueprint priority list of diseases and pathogens prioritized for research and development, affecting several hundreds of thousands of people each year. Lassa fever is spread via infected Natal multimammate mice and also through human-to-human contacts and it is a particular threat to pregnant women. Despite its importance, relatively few mathematical models have been established for modelling Lassa fever transmission up to now. We establish and study a new compartmental model for Lassa fever transmission including asymptomatic carriers, quarantine and periodic coefficients to model annual weather changes. We determine parameter values providing the best fit to data from Nigerian states Edo and Ondo from 2018–20. We perform uncertainty analysis and PRCC analysis to assess the importance of different parameters and numerical simulations to estimate the possible effects of control measures in eradicating the disease. The results suggest that the most important parameter which might be subject of control measures is death rate of mice, while mouse-to-human and human-to-human transmission rates also significantly influence the number of infected. However, decreasing the latter two parameters seems insufficient to eradicate the disease, while a parallel application of decreasing transmission rates and increasing mouse death rate might be able to stop the epidemic.

Lassa haemorrhagic fever; Periodic compartmental model; Data fitting; Disease eradication

1. Background

1.1. Lassa haemorrhagic fever

The first descriptions of Lassa haemorrhagic fever (LHF) or Lassa fever for short date back to the 1950s, though the virus causing LHF was identified later, in 1969 [1]. The disease got its name after the town Lassa in Northeast Nigeria, where the first cases happened. Lassa fever is an acute viral hemorrhagic fever caused by the Lassa virus belonging to the Arenaviridae family. The Natal multimammate rat (Mastomys natalensis), the African wood mouse (Hylomyscus pamfi) and the Guinea multimammate mouse (Mastomys erythroleucus) are hosts of Lassa virus (LASV) in Nigeria [2], [3], [4], [5]. LASV prevalence in the rodent population was two to three times higher in the rainy season, which could be the aftermath of an improved survival of the virus outside the host under wet and relatively cold conditions [6], [7]. Infected Natal multimammate mice shed the virus in urine and droppings. Infection might occur through touching contaminated materials, eating contaminated food, exposure to open cuts. Human-to-human transmission is uncommon and mainly occurs in hospitals and households [8]. Sexual transmission has also been reported [9]. Even after recovery, the virus remains for a long time in bodily fluids: for 3–9 weeks in urine and 3 months in semen. According to the WHO report, Lassa fever is endemic in Nigeria and during the dry season (December–April) following the reproduction cycle of the mice in the wet season (May–June), the annual peak of human cases is usually observed [9]. Virus is more stable when humidity in the atmosphere relatively declines. Transmission from infected rodents to humans mostly occurs inside houses in the dry season when the abundance of rodents is significantly increased [10], [11]. Virus in the urine of rodents might also be a source of infectious airborne droplets. In the dry season, sweeping the floors might generate infectious microaerosols, which may be transmitted to humans, by inhalation of aerosols or inoculation to the mucous membranes [6], [11], [12]. Lassa fever is also endemic in humans in Benin, Ghana, Guinea, Liberia, Mali, Sierra Leone and presumably further countries in West Africa. Here the number of infections per year is estimated between 100,000 and 300,000 with 5,000–10,000 deaths [13], [14]. Lassa menaces mostly those who live in rural areas where multimammate rats are present, especially where poor sanitation and crowded living conditions are typical.

Four out of five people infected with Lassa fever do not show any symptoms or have only mild symptoms, these include fever, tiredness, weakness, and headache. One out of five infected develop a severe multisystem disease. Symptoms of the severe form of the disease include bleeding gums, breathing problems, vomiting, pain in chest, back and abdomen, low blood pressure, facial swelling, hear loss, tremors, encephalitis. The disease has a lethality of approximately 1%, however, it is especially dangerous for women in late pregnancy. For this group, around 29% of the cases results in maternal death, while an 80–95% fetal and neonatal mortality is reported [15], [16], [17]. Lower attack rates have been reported for children than for adults [18].

There are no vaccines for Lassa virus licensed for use in humans yet, and no vaccine candidate has shown enough potency in animal models to have entered phase-I human studies. In the treatment of Lassa fever, mortality rate reduced from 55% to 5% if antiviral ribavirin was applied within the first 6 days of illness. However, only one published trial of ribavirin was seen in treating Lassa fever in humans, which had limited testing of dose [13]. Fluid replacement and the use of blood transfusion required to be monitored carefully [19]. For women in late pregnancy, inducing delivery is necessary.

1.2. Mathematical models for Lassa fever transmission dynamics

Lassa fever was included in the Blueprint list of priority diseases to be prioritized for research and development [20] published by the World Health Organization in 2018. In spite of this, relatively few mathematical modelling studies have been published till now in comparison with other infectious diseases. Bawa et al. [21] established a model with vital dynamics, disease-induced death and infection due to humans, reservoirs and airborne transmissions. James et al. [22] divided infected humans into quarantined and unquarantined compartments and using Lyapunov functions, they showed that the disease is eradicated when the basic reproduction number is less than 1. Onuorah et al. [23] separated male and female human compartments and observed that the basic reproduction number is most sensitive to human birth rate, followed by the condom efficacy and compliance. An age-structured model was proposed by Obabiyi et al. [24] for susceptible, exposed, infected and recovered humans. Recovered human population was viewed as permanently immunized in the model of James et al. [22], Onah et al. [25] and Obabiyi et al. [24]. Recently, Musa et al. [26] included quarantined and non-quarantined states both for exposed and infected and introduced a new compartment for hospitalized people. They also proved a forward bifurcation occurring with a stability switch between the disease-free and the endemic equilibrium. The interaction between human and rodent populations suggests that the initial susceptibility likely increased across the three outbreaks from 2016–2019. Akhmetzhanov et al. [27] quantified the seasonal properties of Lassa fever transmission, showing that migration of rats induced by annual change of weather has a substantial effect in controlling the periodicity of Lassa epidemics. According to this work, rainfall pattern does not affect the transmissibility of the virus directly but negatively and highly correlated with LHF incidence that means seasonal migratory dynamics of rodents play a vital role. Saez et al. [28] suggested a realistic approach including rodent trapping and poisoning, environmental and personal hygiene, house repairs and rodent-proof storage and developing a research-based project for rodent management. Zhao et al. [29] reported direct rainfall impact on LHF epidemics and quantified this impact. Davies et al. [30] used a mathematical model capturing seasonal transmission between rodents and humans, assessing the potential outcomes of an introduction of a vaccination program in affected areas. In [31], a model was established with humans differentiated according to the severity of the disease and with time-periodic parameters for rodent birth rate and carrying capacity of the environment with respect to rodents. The basic reproduction number was introduced as the spectral radius of a linear integral operator and it was shown to serve as a threshold parameter concerning the global dynamics: the disease-free periodic solution is globally asymptotically stable in the case of ${\mathcal{R}}_0<1$, while the disease persists if ${\mathcal{R}}_0>1$.

2. Compartmental model with periodic parameters

We have developed a compartmental model based on earlier models for LHF transmission, at the same time extending those models from several points of view. We follow [26] in introducing quarantine and considering logistic population growth for rodents. In our model, the total human population at time t, denoted by $N_h(t)$, is split into the population of those in quarantine (denoted by $N_q(t)$) and those not in quarantine (denoted by $N_u(t)$), so that

$$N_h(t)=N_u(t)+N_q(t).$$

The total population of individuals in quarantine at time t is divided into those that are susceptible ($S_q(t)$), exposed ($E_q(t)$), that is, infected but not yet infectious and symptomatic ($I_q(t)$). Hence,

$$N_q(t)=S_q(t)+E_q(t)+I_q(t).$$

Similarly, the total population of individuals not in quarantine at time t is subdivided into the sub-populations of susceptible ($S_u(t)$), exposed ($E_u(t)$), infected who do not show any symptoms or have only mild symptoms ($I_u^m(t)$), symptomatic ($I_u^s(t)$), treated ($I_T(t)$), recovered ($R_h(t)$), so that

$$N_u(t)=S_u(t)+E_u(t)+I_u^m(t)+I_u^s(t)+I_T(t)+R_h(t).$$

The total rodent (reservoir) population at time t, represented by $N_r(t)$, is split into two compartments of susceptible ($S_r(t)$) and infected ($I_r(t)$) rodents. Hence, we have

$$N_r(t)=S_r(t)+I_r(t).$$

We denote by Λ and $d_h$ the birth and death rates of humans, respectively. There is also an additional disease-induced death rate, denoted by ${\delta }_s,{\delta }_q$ and ${\delta }_T$ for those in the compartments $I_u^s$, $I_q$ and $I_T$, respectively. Unlike most models where quarantine is included, we follow Lipsitch et al. [32] in the introduction of quarantine. Namely, in most models, quarantine is described in a way that is rather suitable to model isolation, i.e., the removal of individuals who already have been infected, instead of quarantine, meaning the temporary separation of susceptibles who are feared to have been exposed to the disease via contact with an infectious individual or having visited infected areas. Accordingly, in our model, the human-to-human transmission rate is split to the product of the average number of contacts (κ) and the probability of transmission per contact (b), while q stands for the fraction of those of susceptible individuals who are feared exposed and hence moved to quarantine. Unquarantined susceptibles may leave their compartment following a contact with an infectious individual (i.e. someone from the compartments $I_u^m,I_u^s,I_q$ or $I_T$). A fraction b of those contacting an infectious human will contract the disease and hence move to one of the two exposed classes, depending on whether they are moved to quarantine: a fraction q of them arrive in the quarantined exposed compartment $E_q$, while the remaining fraction $1-q$ arrive in the unquarantined exposed compartment $E_u$. A fraction $1-b$ of those susceptible humans contacting an infectious individual will not be infected, however, a fraction q of them will be moved to quarantine because of their previous contact with an infected person, hence, these people will move to the $S_q$ compartment. Individuals in quarantine who turn out to be healthy will move back to the $S_u$ class at a rate $r_q$ at the end of their quarantine period. Those exposed who are not moved to quarantine will arrive in the compartment $E_u$. A fraction θ of these will have only moderate symptoms or no symptoms at all, these move to the compartment $I_u^m$ by rate ${\nu }_u$, those who develop more severe symptoms move to $I_s^m$. We assume that no quarantined infected remain undetected, so all quarantined exposed will move to the compartment $I_q$ by rate ${\nu }_q$. We also introduce a compartment for the most severely infected, who need hospital treatment, denoted by $I_T$. Infected individuals from both $I_u^s$ and $I_q$ may move to this compartment. Recovered patients arrive at the compartment $R_h$.

We assume a logistic growth for the mouse population, however, in our model, a logistic term is included both in the equations for $S_r^{\prime }$ and for $I_r^{\prime }$ assuming that the fraction of infected among newborn mice is proportional to the fraction of infected among the whole rodent population. On one hand, this way we include vertical transmission of Lassa among rodents [33], on the other hand we can make sure that $S_r$ remains positive. Carrying capacity of the environment w.r.t. mice is denoted by K. The notation σ is applied for growth rate of mice. A susceptible mouse may move to the infected class by contracting the disease either by infection from an infected mouse or an infected human. Just like for human-to-human transmission, we introduce different rates for transmission from different compartments of humans to rodents. Mouse-to-mouse transmission rate is denoted by ${\beta }_r$. Following [26], we use standard incidence for human-to-human and rodent-to-human transmission, while mass action incidence is used for interspecies transmission.

Lassa fever incidence shows a strong seasonal behaviour: the number of Lassa cases in humans reaches its peak during dry season (December–April) through direct and indirect contact between rodents and humans [10]. During this time of the year, mice come closer to humans in search for food, increasing rodent-to-human contacts. Mouse population itself is also heavily influenced by the annual change of weather. To capture this phenomenon, we introduce time-periodic parameters for rodent birth rate (σ), carrying capacity of the environment with respect to rodents ($\overline{K}$), as well as for rodent-to-human and human-to-rodent transmission rates (${\overline{\tau }}_s,{\overline{\tau }}_m,{\overline{\tau }}_q,{\overline{\tau }}_T,{\overline{\tau }}_r$).

From the above, the main novelties of our model are a different description of quarantine, the inclusion of asymptomatic carriers of the disease, vertical transmission in rodents and the introduction of time-periodic parameters to describe seasonal behaviour of the mouse population.

The transmission diagram of our model is shown in Fig. 1. A complete description of the model parameters is summarized in Table 1. The system is given by the equations, our model takes the form:

$$S_u^{\prime }(t)=\mathrm{\Lambda }-\kappa b{\lambda }_h(t)S_u(t)-q\kappa (1-b){\lambda }_h(t)S_u(t)-{\lambda }_{hr}(t)S_u(t)-d_h{S}_u(t)+r_q{S}_q(t)+\xi R_h(t),E_u^{\prime }(t)=(1-q)\kappa b{\lambda }_h(t)S_u(t)+{\lambda }_{hr}(t)S_u(t)-{\nu }_u{E}_u(t)-d_h{E}_u(t),{I_u^m}^{\prime }(t)=\theta {\nu }_u{E}_u(t)-{\gamma }_m{I}_u^m(t)-d_h{I}_u^m(t),{I_u^s}^{\prime }(t)=(1-\theta ){\nu }_u{E}_u(t)-{\eta }_s{I}_u^s(t)-(d_h+{\delta }_s)I_u^s(t),S_q^{\prime }(t)=q\kappa (1-b){\lambda }_h(t)S_u(t)-{\lambda }_{hr}(t)S_q(t)-r_q{S}_q(t)-d_h{S}_q(t),E_q^{\prime }(t)=q\kappa b{\lambda }_h(t)S_u(t)+{\lambda }_{hr}(t)S_q(t)-{\nu }_q{E}_q(t)-d_h{E}_q(t),I_q^{\prime }(t)={\nu }_q{E}_q(t)-{\eta }_q{I}_q(t)-{\gamma }_q{I}_q(t)-(d_h+{\delta }_q)I_q(t),I_T^{\prime }(t)={\eta }_s{I}_u^s(t)+{\eta }_q{I}_q(t)-{\gamma }_T{I}_T(t)-(d_h+{\delta }_T)I_T(t),R_h^{\prime }(t)={\gamma }_m{I}_u^m(t)+{\gamma }_T{I}_T(t)+{\gamma }_q{I}_q(t)-\xi R_h(t)-d_h{R}_h(t),S_r^{\prime }(t)=\sigma (1-\frac{N_r(t)}{K(t)})S_r(t)-{\lambda }_r(t)S_r(t)-{\lambda }_{rh}(t)S_r(t)-d_r{S}_r(t),I_r^{\prime }(t)=\sigma (1-\frac{N_r(t)}{K(t)})I_r(t)+{\lambda }_r(t)S_r(t)+{\lambda }_{rh}(t)S_r(t)-d_r{I}_r(t),$$ (1)

where the forces of infection ${\lambda }_h(t),{\lambda }_{hr}(t),{\lambda }_r(t)$ and ${\lambda }_{rh}(t)$ are given as

$${\lambda }_h(t)=\frac{I_u^s(t)+{\beta }_m{I}_u^m(t)+{\beta }_q{I}_q(t)+{\beta }_T{I}_T(t)}{N_h(t)},{\lambda }_{hr}(t)={\tau }_r(t)I_r(t),{\lambda }_r(t)={\beta }_r\frac{I_r(t)}{N_r(t)},{\lambda }_{rh}(t)={\tau }_s(t)I_u^s(t)+{\tau }_m(t)I_u^m(t)+{\tau }_q(t)I_q(t)+{\tau }_T(t)I_T(t).$$

As seen in the description of the model, there are six time-dependent parameters $K(t)$, ${\tau }_r(t)$, ${\tau }_s(t)$, ${\tau }_m(t)$, ${\tau }_q(t)$ and ${\tau }_T(t)$. Based on earlier works using trigonometric functions for seasonal parameters (see e.g. [34], [35], [36]) and adjusted to follow the pattern of rainy season better, these time-dependent parameters take the form $C\cdot (a+{\cos }^{10}(c+\frac{\pi t}{52}))$ where $C\in \{\overline{K},{\overline{\tau }}_r,{\overline{\tau }}_s,{\overline{\tau }}_m,{\overline{\tau }}_q,{\overline{\tau }}_T\}$ with $\overline{K},{\overline{\tau }}_r,{\overline{\tau }}_s,{\overline{\tau }}_m,{\overline{\tau }}_q,{\overline{\tau }}_T\in {\mathbb{R}}^{+}$.

Figure 1.

Transmission diagram. Blue arrows indicate transition from one compartment to another, green arrows indicate new entry for rodents and humans. Light and dark coloured boxes depict noninfected and infected compartments both for humans and for mice, respectively.

Table 1.

Description of parameters of model (1).

Parameters	Description
Λ	Recruitment rate for humans
dh	Natural death rate of humans
dr	Natural death rate of rodents
δs,δq,δT	Disease-induced death rates for infected human compartments
κ	Average per capita contact rate in the community
b	Transmission probability per contact
q	Quarantine rate of susceptible individuals
βm,βq,βT	Relative human-to-human transmissibilities for various compartments
βr	Rodent-to-rodent transmission rate
${\overline{\tau }}_s,{\overline{\tau }}_m,{\overline{\tau }}_q,{\overline{\tau }}_T$	Baseline value of human-to-rodent transmission rates
${\overline{\tau }}_r$	Baseline value of rodent-to-human transmission rate
θ	Proportion of asymptomatic infections
ηs,ηq	Progression rate from (Is,Iq) to IT
γm,γq,γT	Humans recovery rates
νu,νq	Humans incubation rates
ξ	Rate of relapse from Rh to Sh
rq	Rate of release from quarantine
σ	Maximum growth rate of the rodents
$\overline{K}$	Baseline value of maximal carrying capacity of rodents
a,c	Seasonality parameters

3. Parameter estimation and sensitivity

We fitted our model to data from Nigeria to study the phenomena discussed above. As the area of the whole country is heterogeneous, we have chosen the two neighbouring states Edo and Ondo for fitting. According to Nigeria Centre for Disease Control data [44], these two states have been the ones with the highest numbers of Lassa cases. Fig. 2 shows the location of these two states within Nigeria with all states coloured according to the number of cases/million population during the period between 9 September 2018 and 11 July 2020. The map shown in Fig. 2, just like the simulations in the paper, were prepared using the Wolfram Mathematica software.

Figure 2.

States of Nigeria w.r.t. the number of cases between 9 September 2018 and 11 July 2020. States with less than 5 cases/million population are marked with blue, those with number of cases between 5 and 100/million population are marked with yellow. The most infected states (number of cases above 100/million population), including the two states Edo and Ondo are marked with red. Figure created with Wolfram Mathematica.

Due to lack of detailed data available in earlier years, we selected the years 2018–20 for model fitting as in these years, weekly data for all states in Nigeria are available [44]. Unfortunately, the data available to assess parameters regarding the mouse population are rather scarce, hence, our goal could not be to precisely estimate these, we only aimed to give a rough evaluation of the mouse population, which provides an appropriate basis for studying processes regarding infection of humans. Hence, we first looked for parameters supplying plausible solutions for the mouse equations. Following this, we used Latin Hypercube Sampling to find the human-related parameters which provide the best fit to data. This statistical sampling method (see, e.g. [45]) enables a simultaneous variation of all input parameters and it is applied to generate a representative sample set of n-tuples of parameters (where n is the number of parameters fitted) taking values from given ranges. After obtaining this representative set of parameters, we start a solution with all of the parameter sets in this representative set, and then we use the least squares method to find the solution which is the closest to data.

3.1. Parameter estimation

Using the method described above, we fitted our model to data from Edo and Ondo states of Nigeria. Fig. 3 shows the model fitting which reproduces well the two peaks of the epidemic in the years 2019 and 2020. The parameter values which provide the best fit depicted in Fig. 3 are listed in Table 2.

Figure 3.

The best fitting solution plotted with 2018–20 data from Nigerian states Edo and Ondo. Parameter values obtained in the fitting are given in Table 1.

Table 2.

Parameters for model (1) providing the best fit.

Parameters	Baseline (Range)	Units	Sources
Λ	8907290	Weeks−1	[37]
dh	0.00036	Weeks−1	[38]
dr	0.007	Weeks−1	[39]
δs	1.44 (0.1,1.5)	Weeks−1	[26]
δq	0.81 (0.1,1.5)	Weeks−1	[26]
δT	1.03 (0.1,1.5)	Weeks−1	[26]
κ	6.9 (5,18)	Weeks−1	[40]
b	0.02 (0.004,0.07)	Weeks−1	[40]
q	0.36 (0.05,0.5)	Weeks−1	[41]
βm,βq,βT	1.15 (0.01,1.5)	–	[41]
βr	0.00002495	Weeks−1	Fitted
${\overline{\tau }}_s$	6.94⁎10−14 (4.0⁎10−14,1.0⁎10−13)	Weeks−1	Fitted
${\overline{\tau }}_m,{\overline{\tau }}_q,{\overline{\tau }}_T$	4.66⁎10−14 (4.0⁎10−14,1.0⁎10−13)	Weeks−1	Fitted
${\overline{\tau }}_r$	7.77⁎10−14 (4.0⁎10−14,1.0⁎10−13)	Weeks−1	Fitted
θ	0.71 (0.7,0.9)	–	[17]
ηs	0.14 (0.007,0.15)	Weeks−1	[42]
ηq	0.069 (0.007,0.15)	Weeks−1	[40]
γm	0.64 (0.33,1.2)	Weeks−1	[43]
γq	1.01 (0.33,1.2)	Weeks−1	[43]
γT	0.60 (0.33,1.2)	Weeks−1	[43]
νu	0.66 (0.14,1.5)	Weeks−1	[17]
νq	0.04 (0.03,0.3)	Weeks−1	[17]
ξ	0.016 (0.005,0.05)	Weeks−1	[26]
rq	1.359 (0.5,2)	Weeks−1	[41]
σ	0.65	Weeks−1	Fitted
$\overline{K}$	4.99⁎108	–	Fitted
a	1.31 (0.7,1.4)	–	Fitted
c	5.19 (1.5,6)	–	Fitted

To show that in spite of the relatively large number of fitted parameters, the fit is rather robust, in Fig. 4 the best fitting solution is shown alongside the 3% confidence range, which was obtained by letting for all parameters a 3% relative error w.r.t. the best fitting parameters.

Figure 4.

The best fitting solution with parameter values in Table 1 plotted with the 3% confidence range. The band around the best fitting solution was obtained by letting all of the fitted parameters vary ±3%.

3.2. Sensitivity and uncertainty analysis

To assess the importance of the possible intervention parameters, we performed Partial Rank Correlation Coefficients (PRCC) analysis. This method allows us to rank the effect of different parameters on the outcome, when parameters are simultaneously varied and to find out the statistical relationships between the input parameters and the outcome value (see, e.g. [46]). Parameters with positive PRCC values are positively correlated with the outcome value, that is, the number of cumulative cases increases as these parameter values are increased, while increasing parameters with negative PRCC will result in a smaller number of cumulative cases. This method enables us to determine which are the key parameters which might be changed due to various control measures. In our work, the five input parameters were selected as average number of contacts among humans (κ), transmission probability per contact among humans (b), quarantine rate (q), rodent-to-human transmission rate (${\tau }_r$) and death rate of mice ($d_r$), while the output parameter was the cumulative number of cases.

Performing the PRCC analysis for the parameters that might be subject to control measures, we obtained the results shown in Fig. 5. The results suggest that the most important parameter is mice death rate, i.e. the most effective way to reduce Lassa transmission is suggested to be culling of mice. However, decreasing human-to-human and rodent-to-human transmission rates – e.g. by increasing hygiene levels, installing protection against mice, quitting the consuming of mice – are also shown to have a substantial effect on reducing the disease burden. Decreasing human contact rates seems to have a smaller effect, furthermore, such an intervention is unlikely to be sustained for a longer period. Out of the parameters involved in this analysis, quarantine rate proved to have the lowest effect.

Figure 5.

Partial rank correlation coefficients (PRCCs) of the five parameters that might be subject to intervention measures in controlling Lassa fever. Increasing parameters with positive PRCC value will increase the number of cases, increasing ones with negative PRCC will decrease the number of cases.

Besides the above sensitivity analysis, we performed uncertainty analysis to assess uncertainties which are expected to arise in the estimates of the parameter values. We used again the Latin Hypercube Sampling method with 15,000 runs considering the baseline values of the various parameters considered in the fitting in Subsection 3.1 given in Table 2, allowing all parameters to change $\pm 20\text{\%}$ w.r.t. the baseline values and taking the cumulative number of infected as response function. The results of the uncertainty analysis suggest that the cumulative number of infected lies in the range $(498,2920)$ with an approximate median 1293 (see Fig. 6).

Figure 6.

Box plot of the cumulative number of infected. Baseline values for parameters fitted in subsection 3.1 are given in Table 2.

As pointed out above, data regarding the mouse population is scarce and thus rodent-related parameters are more difficult to estimate than other parameters of the model. Hence, we prepared a similar box chart concentrating on the rodent-related parameters $\overline{K},\sigma ,d_r,{\beta }_r,{\overline{\tau }}_s,{\overline{\tau }}_r,{\overline{\tau }}_m,{\overline{\tau }}_q,{\overline{\tau }}_T$. The median is approximately 1323, while the cumulative number of infected lies in the range $(1275,1377)$ (see Fig. 7).

Figure 7.

Box plot of the cumulative number of infected with variation of the rodent-related parameters. Parameter values are given in Table 2.

4. Effect of possible control measures

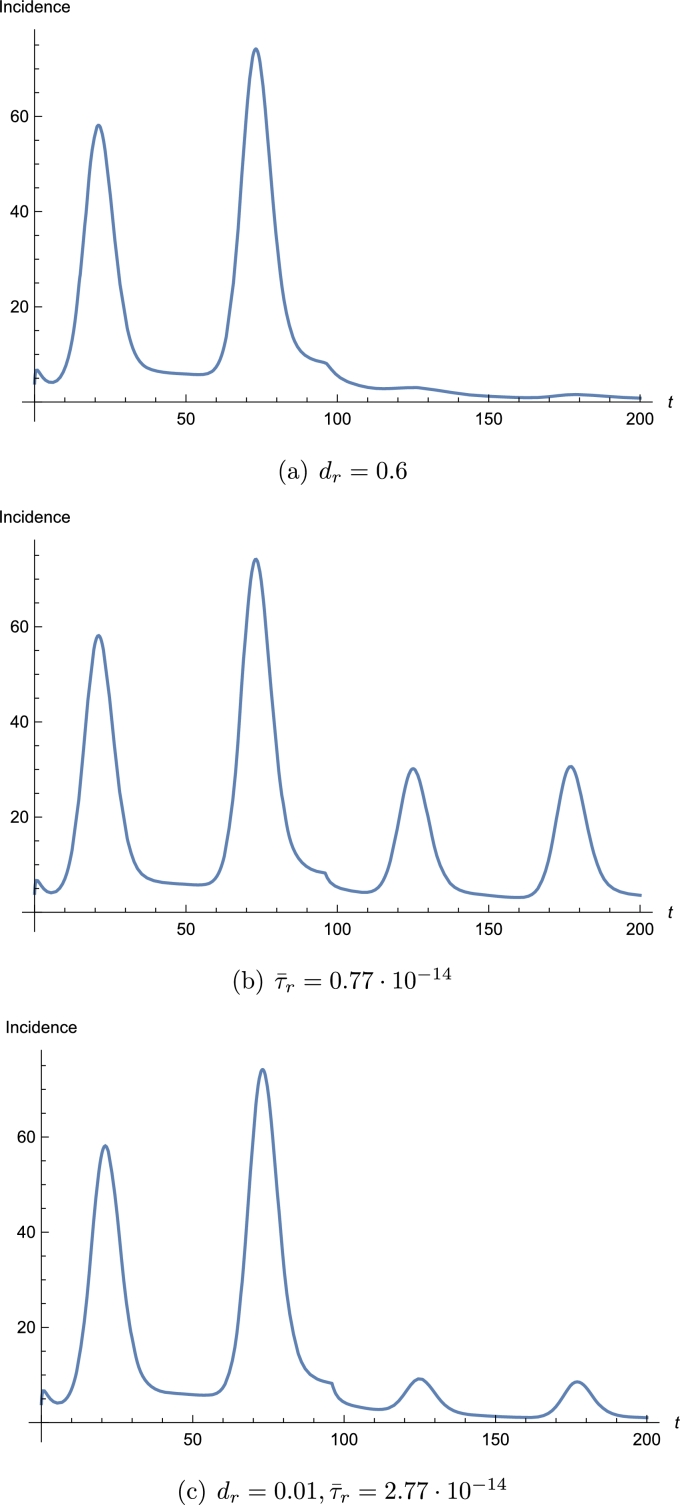
We have performed simulations to see what kind of possible effects the change of some parameters might result in. To this end, we selected those parameters which are most likely to be modified due to some control measures, namely the average number of contacts, human-to-human and rodent-to-human transmission rates, quarantine rate and mice death rate. Our aim was to see what degree of change of these parameters might turn out to be sufficient to prevent a periodic recurrence of Lassa fever. The simulations were started with the fitted parameters up to week 96, where a modification of one or more parameters was introduced.

We observed from the simulation that the most influential parameter is $d_r$. Increasing the death rate of the rodents $d_r$ by mice culling can decrease the number of infected and even turn the disease to a complete extinction (see Fig. 8(a)). Although mice are generally regarded as a nuisance for contaminating and destroying food and belongings [28], their culling in such large extents should probably not be performed as killing mice being a member of any food chains might result in unexpected harms for other species. At the same time, culling is very unlikely to be applied as a key control strategy to curtail the spread of Lassa fever. Hence, other measures should be applied which decrease interactions between humans and rodents [47]. Rodents should be kept out of homes and food supplies should be protected from them by using rodent-proof food containers. Garbage should be collected distant from homes. All these measures serve to reduce rodent-to-human transmission. We noticed from the simulations that decreasing the rodent-to-human transmission rate ${\overline{\tau }}_r$ also decreases the number of infected, but just this measure is unable to drive the disease to extinction (see Fig. 8(b)). A parallel application of the above two measures – a smaller, but targeted culling, e.g. trapping inside and around the houses and reduction of rodent-to-human transmission rate – can be successful, and decreasing mouse-to-human transmission rate allows a much smaller killing rate of mice (see Fig. 8(c)). Further protective measures may aim to reduce human-to-human transmission rates by increasing personal hygiene, using gloves and masks when contacting an infected person. In the model, human-to-human transmission rates might be reduced by decreasing the transmission probability b or the number of human contacts κ or increasing the quarantine rate q. However, our simulations suggest that applying these three measures does not help much without modifying the rodent-related parameters. However, an opposite change of non-rodent-related parameters might even result in a significant increase of Lassa cases. If q is increased and b and κ are decreased, a slightly smaller change in ${\overline{\tau }}_r$ is sufficient to achieve the same result as without non-rodent-related measures.

Figure 8.

Effect of parameter changes that might mitigate or eradicate the Lassa epidemic. Parameter values modified w.r.t. the best fit are given in the caption above. The rest of the parameters are selected as in Table 2.

5. Conclusions

In this work, we have established a compartmental model for Lassa fever transmission by extending previous models in various ways. In the model, we tried to include the most important features of earlier models including human-to-human and vector-borne transmission as well as vertical transmission in mice. The model also considers the effect of quarantine, which we described following [32] such that quarantining is based on contacts with infected individuals. Given the large percentage of those infected who do not show any symptoms or have only lesser symptoms, we also incorporated in our model a compartment for those mildly infected. As Lassa fever dynamics shows a strong seasonal behaviour due to the influence of the annual change of weather on mouse populations and due to the fluctuating level of human–rodent contacts, we made our model time-dependent by making some of the rodent-related parameters time-periodic.

The main novelties of the model introduced in this work are the inclusion of asymptomatic carriers of the disease, vertical transmission in rodents, including time-dependent parameters to consider the effects of the annual change of weather on the behaviour of mice. Also, we modelled quarantine in a way which had not been previously used in models for Lassa fever transmission. This method of describing this phenomenon enables us to take account of those who are moved to quarantined because of being feared to have contracted the disease, but at the end turn out to be healthy. The model is validated by fitting to 2018–20 data from the two Nigerian states Edo and Ondo, which have been effected by the disease in the largest scale within Nigeria. Thanks to the application of the time-dependent parameters which are aimed to follow the annual fluctuations of parameters regarding mouse population dynamics and human–rodent contacts, the fitted solution reproduces reasonably well the peaks observed in the dry seasons of the two subsequent years studied in the paper.

Of course, our model also has its limitations. As described above, due to a lack of sources, we have encountered several uncertainties regarding the mouse population, several parameter values are hard to identify based on existing literature. Also, we have a rather large number of parameters fitted, which, of course, creates uncertainties as different parameter sets might provide similar results. However, the fit seems rather robust in the sense that even with a simultaneous variation of all parameters, the solutions remain close to the fitted one. Based on this, we expect that even in case of different parameters, the overall dynamics remains similar and modifying certain parameters would have similar effects as in the cases studied in the present paper. A successful implementation of the control measures studied in our simulations could provide further evidence for the role of the mice.

Using the fitting obtained, we performed sensitivity and uncertainty analysis and numerical simulations to assess the effect of different parameters on the number of infected cases, especially those parameters which might be subject to some intervention measures in order to estimate how various controls might contribute to “flatten the curve”. The results of sensitivity analysis and numerical simulations suggest that mouse-to-human transmission rate and mouse death rate are among the most important parameters and hence the abundance of mice is the most important driver of Lassa fever transmission. This is also justified by the seasonal pattern of the epidemic, following the seasonal variation of mice populations due to weather fluctuation. These results are in accordance with those of earlier works, e.g. [26], [27], [29]. Furthermore, our results suggest that culling of mice can result in eradicating the epidemic. Culling of rodents being an unlikely solution, we studied the possible effects of other control measures: decreasing rodent-to-human transmission e.g. by using rodent-safe food containers and collecting garbage far from the houses, as well as decreasing human-to-human transmission. Based on our simulations, modifying control parameters corresponding to such measures might mitigate the epidemic, but they seem to be insufficient to drive the epidemic to extinction. However, applying these measures enables us to stop transmission even with a much smaller rate of culling mice which might be achieved via a targeted culling, e.g. trapping mouses around and inside houses.

Further development of the model might include an age-structured model to consider the different attack rates reported for various age groups. A further possibility is to differentiate the two sexes among humans to include sexual transmission as well. This would also enable us to take account of the prevalence among pregnant women, who are most endangered by the disease.

Declarations

Author contribution statement

S. Barua, A. Dénes, M.A. Ibrahim: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Wrote the paper.

Funding statement

This research was supported by grant TUDFO/47138-1/2019-ITM of the Ministry for Innovation and Technology, Hungary. A.D. was supported by the János Bolyai Research Scholarship of the Hungarian Academy of Sciences, by the project no. 128363, implemented with the support provided from the National Research, Development and Innovation Fund of Hungary, financed under the PD_18 funding scheme. S.B. was supported by Stipendium Hungaricum scholarship and Ministry of Education, Government of Bangladesh. M.A.I. was supported by Stipendium Hungaricum scholarship and a scholarship from the Ministry of Higher Education of the Arab Republic of Egypt.

Data availability statement

All data generated or analysed supporting the findings of this article are included within the article or are available upon request.

Declaration of interests statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.