Figure 3.

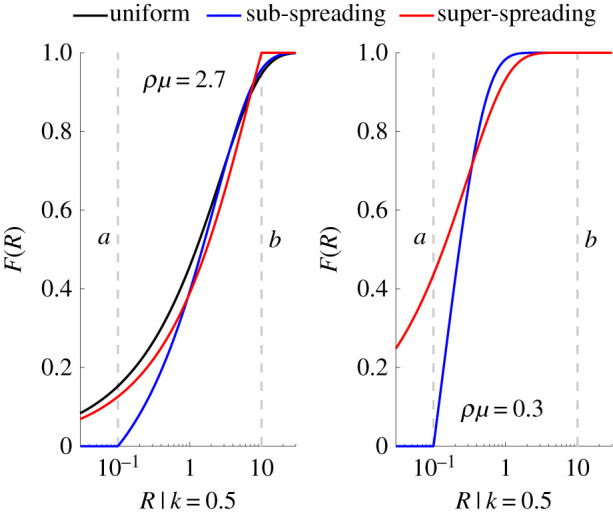
Control strategies shape reproduction number distributions. We plot the cumulative distribution function of the event reproduction number, F(R), for uniform, super-spreading (upper truncation b) and sub-spreading (lower truncation a) control measures under a renewal model with dispersion k = 0.5 at the largest and smallest mean controlled reproduction numbers, ρμ, examined in figure 2. We find that super-spreading control is best (in terms of variance-to-mean ratios) at large ρμ because there is a notable probability of super-spreading events that becomes truncated under this measure, i.e. the resulting F(R) curve rises to 1 first due to R > b events being controlled. However, when ρμ is small this becomes vastly less important (the super-spreading and uniform controls converge) and the F(R) curve under sub-spreading control rises the fastest to 1 (where R < a events are suppressed).