Bayesian ROC curve estimation under verification bias

Abstract

Receiver operating characteristic (ROC) curve has been widely used in medical science for its ability to measure the accuracy of diagnostic tests under the gold standard. However, in a complicated medical practice, a gold standard test can be invasive, expensive, and its result may not always be available for all the subjects under study. Thus, a gold standard test is implemented only when it is necessary and possible. This leads to the so-called ‘verification bias’, meaning that subjects with verified disease status (also called label) are not selected in a completely random fashion. In this paper, we propose a new Bayesian approach for estimating an ROC curve based on continuous data following the popular semiparametric binormal model in the presence of verification bias. By using a rank-based likelihood, and following Gibbs sampling techniques, we compute the posterior distribution of the binormal parameters intercept and slope, as well as the area under the curve by imputing the missing labels within Markov Chain Monte-Carlo iterations. Consistency of the resulting posterior under mild conditions is also established. We compare the new method with other comparable methods and conclude that our estimator performs well in terms of accuracy.

1. Introduction

The receiver operating characteristic (ROC) curve for a long time has been widely used in diagnostic medicine [1] because of its ability to incorporate accuracy of all decision rules in a curve plotted in the unit square. When the true disease status of each study subject is known by the most accurate diagnostic test called the gold standard test, the ROC curve has been used to compare the accuracy of other available diagnostic test(s) to the gold standard test. The ROC curve is the plot of the true positive rate (abbreviated as TPR, also called sensitivity) versus the false positive rate (abbreviated as FPR, also called one minus specificity) by varying a decision threshold value c. The decision threshold value c is used to determine the diagnostic result as positive, or negative, depending on whether the test is not less than, or less than c, respectively.

Because gold standard tests may be invasive and expensive, it is more ethical that verification of the true disease status of study subjects would generally be obtained only for high risk subjects according to the screening test. For example, liver biopsy is considered as the gold standard in evaluating chronic hepatitis and fibrosis. It costed on an average over US $1000 in 2004 without complications and about US $3000 with complications [2]. Further, liver biopsy procedure is invasive. Complications of liver biopsy include significant bleeding and hospitalization. Fatal complications have been reported up to 0.038% among the biopsy patients [3].

Because of a differential in the chance of verification between subjects with high and low risk, it follows that the verified subjects are not sampled randomly from the population. Hence, an estimator of the accuracy of a diagnostic test given by the area under the ROC curve (AUC) based on only the subjects with labels may be biased. This is known as the verification bias. Correcting for the verification bias involves dealing with the missing data. Here, we use the commonly used assumption for missing verification of disease status, assuming missing at random (MAR) introduced by Little and Rubin [4], which means the chance of missing the verification of disease status is independent of the disease itself conditional on the observed measurements.

In this paper, we focus on the problem of estimating diagnostic accuracy of a single test in the presence of verification bias. When the screening test is binary or ordinal, under the MAR assumption, Begg and Greenes [5] proposed an adjusted estimate of TPR and FPR. Other more efficient methods are discussed by Reilly and Pepe [6], Zhou [7], Clayton et al. [8]. Gastwirth, Johnson and Reneau [9] adopted a Bayesian analysis to estimate sensitivity and specificity of a rare diseases for binary outcomes. When the diagnostic test is continuous, under the MAR assumption, Alonzo and Pepe [10] considered the empirical estimate of an ROC curve. They extended some existing imputation and re-weighting methods designed for discrete diagnostic tests to the continuous ones in estimating TPR and FPR. On the basis of the empirical ROC curve estimate, and by using the trapezoidal rule for integration [11], the estimate of the AUC can be obtained. Their verification bias-corrected estimators are dependent on the modeling of the probability of verification status, and disease status given the screening test result and covariates. A different direction of research deals with nonignorable missing mechanism, which assumes a specific model for the probability of the verification of true disease status, depending on the true disease status. Some early work was performed by Zhou [12, 13] and Kosinski and Barnhart [14]. Recently, Rotnitzky, Faraggi, and Schisterman [15] suggested a doubly robust AUC estimator. Fluss et al. [16] extended Rotnitzky et al. [15]’s method and obtained the asymptotic properties of their estimator.

All of the existing methods differ in modeling the mechanism of the missingness. Throughout the literature on estimation of ROC curves for continuous diagnostic variables, the most popular semi-parametric model of ROC curve assumes binormality. In the binormal model, the diagnostic test variables of non-diseased and diseased groups are normally distributed after some monotone increasing transformation H. Currently, there is no verification bias-corrected method available to estimate the ROC curve under the binormality assumption.

In the absence of the verification bias, a Bayesian method using a rank-based likelihood (BRL) was introduced by Gu and Ghosal [17]. Exploiting the invariance of the rank-likelihood with respect to monotone transformations, they eliminated the need of introducing a prior distribution on the underlying monotone transformation H in the binormal model. They developed Gibbs sampling techniques to simulate samples from the posterior distribution of the parameters in the binormal model, which are obtained to construct a Bayes estimator.

Our proposed verification bias-corrected estimator of ROC is an appropriate modification of the BRL method in the situation with missing labels. We assume that the probability of having labels is a monotone function of the diagnostic measurement. Then the distribution of the unobserved labels conditional on the observations can be easily computed using the Bayes theorem. Hence the missing labels can be imputed within the Gibbs sampling scheme of the BRL method. Coupled with this additional step, the BRL method is hence extended in this partial gold standard situation and will be abbreviated as PG-BRL.

The following notations will be used. Let ϕ and Φ stand for the density and cumulative distribution function (CDF) of standard normal distribution, respectively, and $\stackrel{\_}{\Phi }=1-\Phi$. We use ϕ_(μ,σ) to denote the density function of the normal distribution N(μ, σ²) with mean μ and standard deviation σ. Let TN(μ, σ², (e₁, e₂)) denote N(μ, σ²) distribution truncated to the interval (e₁, e₂), where e₁ < e₂, e₁, $e_2\in \mathbb{R}\cup \{-\infty ,\infty \}$.

The paper is organized as follows. The methodology is described in Section 2. In Section 3, we obtain posterior consistency. Simulation studies and real data analysis are provided in Sections 4 and 5, respectively. Estimation with covariates, and with nonignorable missing mechanism is also discussed in Section 6.

2. Description of the methodology

2.1. Notation

Let S = S_N = (S₁, …, S_N) = (X, Y) be the diagnostic measurements associated with N subjects under study, where X and Y are defined in this section. We denote the number of observations from healthy and diseased groups by m and n, respectively, m + n = N. Let D₁, …, D_N stand for the true disease status of subjects, where 0 means healthy, and 1 means disease. Thus $m={\sum }_{i=1}^N\mathbb{1}(D_i=0)$, and $n={\sum }_{i=1}^N\mathbb{1}(D_i=1)$, where $\mathbb{1}$ stands for the indicator function.

Under the partial gold standard scenario, we only observe a small fraction of subjects having the true disease status D_i, i = 1, …, N. Let L = (L₁, …, L_N), where L_i is defined by

$$L_i=\{\begin{array}{ll}0,& \text{if label is observed and}{D}_i=0,\\ 1,& \text{if label is observed and}{D}_i=1,\\ 2,& \text{if label is not observed}.\end{array}$$ (1)

Observe that in this representation, one single variable carries information on missingness, as well as the labels if observed.

Let m* and n* stand for the number of observations having labels from healthy and diseased groups, respectively, that is, $m^{*}={\sum }_{i=1}^N\mathbb{1}\left(L_i=0\right)$, $n^{*}={\sum }_{i=1}^N\mathbb{1}\left(L_i=1\right)$ and put N* = m* + n*. Let X = X_m = (X₁, …, X_m) = (S_i : D_i = 0, i = 1, …, N) and Y = Y_n = (Y₁, …, Y_n) = (S_i : D_i = 1, i = 1, …, N). Note that X and Y are not observable. Let H be the unknown monotone increasing transformation making the transformed observations normally distributed as described in (2). Let the transformed measurements denoted by Z = H(X), W = H(Y), and Q = H(S). Let $\tilde{\mathit{Q}}$, $\tilde{\mathit{S}}$, $\tilde{\mathit{L}}$, and $\tilde{\mathit{D}}$ stand for the order statistic of Q, the order statistic of S, the labeling and the disease status corresponding to $\tilde{\mathit{Q}}$, respectively. Moreover, let ${\tilde{Q}}_k$ and ${\tilde{S}}_k$ denote the kth element $\tilde{\mathit{Q}}$ and $\tilde{\mathit{S}}$, respectively.

Let the rank of S be R_N = R(S) = (R(S₁), …, R(S_N)) = (R_N1, …, R_NN). Define the collection of unobserved and observed labels as D_un = {D_i : L_i = 2, i ⩽ N} and D_obs = {D_i : L_i = 0 or 1, i ⩽ N} , respectively.

2.2. Model

We assume the disease prevalence rate in the population is 0 < λ < 1, that is, the underlying true disease labels for N subjects as $D_i\stackrel{\text{i.i.d.}}{\sim }\text{Bin}\left(1,\lambda \right)$. Conditional on the labels, we have $S_i|\left\{D_i=0\right\}\stackrel{\text{i.i.d.}}{\sim }F$, $S_i|\left\{D_i=1\right\}\stackrel{\text{i.i.d.}}{\sim }G$, where F and G are continuous CDFs. We assume the binormality assumption holds, that is, there exists some strictly monotone increasing transformation H, such that

$$Q_i|\left\{D_i=0\right\}\stackrel{\text{i.i.d.}}{\sim }\text{N}\left(0,1\right);Q_i|\left\{D_i=1\right\}\stackrel{\text{i.i.d.}}{\sim }\text{N}\left(\mu ,{\sigma }^2\right),\mu >0,$$ (2)

where Q_i = H(S_i).

It is well known that the ROC curve under binormality is given by

$$R\left(t\right)=\Phi \left(a+b{\Phi }^{-1}\left(t\right)\right),\text{where}a\text{=}\mu /\sigma ,b=1/\sigma .$$ (3)

The area under the ROC curve (AUC) also has an explicit form

$$\text{AUC}=\Phi \left(\frac{a}{\sqrt{1+b^2}}\right)=\Phi \left(\frac{\mu }{\sqrt{1+{\sigma }^2}}\right).$$ (4)

Typically, in a clinical practice, doctors will prescribe more accurate diagnostic test to the patients only if their screening test results show high risk of disease of interest. In particular, subject with a higher diagnostic result will have higher chance of being forwarded to a more thorough gold standard test. Hence, missing the gold standard test completely at random is not an appropriate assumption. In general, we can model the probability of verifying the disease status as

$$\text{P}\left(L_i\ne 2|Q_i,D_i\right)=g\left(Q_i\right),$$ (5)

where g is a monotone increasing function. Note that Q_i’s are masked by the unknown transformation H. Hence Q_i’s are actually not observed.

Alonzo and Pepe [10] specified the following model based on observed S:

$$P\left(L_i\ne 2|S\right)=\{\begin{array}{ll}1,& \text{if}S\text{>}{S}_{\left(p_1,N\right)},\\ p_2,& \text{otherwise},\end{array}$$ (6)

Here, p₁ and p₂ are probabilities known from data source. Because Qs and Ss have the same ordering, (6) can be rewritten as a special case of (5) with

$$g\left(Q\right)=\{\begin{array}{ll}1,& \text{if}Q\text{>}{Q}_{\left(p_{1}N\right)},\\ p_2,& \text{if}Q⩽Q_{\left(p_{1}N\right)}.\end{array}$$

Another reasonable model uses the probit link:

$$\text{P}\left(L_i\ne 2|Q_i\right)=\Phi \left(\alpha +\beta Q_i\right),\alpha ,\beta \text{unknown and}\beta >0.$$ (7)

2.3. Prior distribution

We will follow a Bayesian approach to estimate (λ, μ, σ), equivalently, (λ, a, b). The prior distributions are described as follows:

• The disease prevalence λ ~ Beta(l₁, l₀), where l₁ and l₀ are chosen to match the mean and the standard error from our prior knowledge, that is, l₁ and l₀ are chosen to equate to l₁/(l₁ + l₀) with the prior guess for the population prevalence of disease and $\sqrt{l_0{l}_1}/\left(\left(l_0+l_1\right)\sqrt{l_0+l_1+1}\right)$ with the anticipated uncertainty in the prior guess.

• In general, it is difficult to specify a subjective prior for (μ, σ). We choose the most commonly used improper prior π(μ, σ) ∝ σ⁻¹ for location-scale parameters.

2.4. Posterior distribution

2.4.1. Invariant set.

Under the binormality assumption (2), the ranks and labels of Q, denoted by R(Q) and L(Q), respectively, are invariant after the transformation H on S. Therefore, a set D_obs invariant under the action of H can be defined as follows [17]:

$$\begin{gathered} {\mathcal{D}}_{\text{obs}}=\left\{\left(\mathit{z},\mathit{w}\right)\in {\mathbb{R}}^{m+n}:R\left(\mathit{z},\mathit{w}\right)=R\left(\mathit{S}\right),L\left(\mathit{z},\mathit{w}\right)=L\left(\mathit{S}\right)\right\}, \\ =\left\{\left(\mathit{z},\mathit{w}\right)\in {\mathbb{R}}^{m+n}:{\underset{\_}{z}}_k<z_k<{\overline{z}}_k,{\underset{\_}{w}}_l<w_l<{\overline{w}}_l\forall k,l,L\left(\mathit{z},\mathit{w}\right)=L\left(\mathit{S}\right)\right\}, \end{gathered}$$ (8)

where z = (z₁, …, z_m), w = (w₁, …, w_n), and

$${\underset{\_}{z}}_k=\underset{i}{\max }\left\{z_i:R_{Ni}<R_{Nk}\right\}\vee \underset{j}{\max }\left\{w_j:R_{N\left(m+j\right)}<R_{Nk}\right\},$$

$${\overline{z}}_k=\underset{i}{\min }\left\{z_i:R_{Nk}<R_{Ni}\right\}\wedge \underset{j}{\min }\left\{w_j:R_{Nk}<R_{N\left(m+j\right)}\right\},$$

$${\underset{¯}{w}}_l=\underset{i}{\max }\left\{z_i:R_{\mathit{Ni}}<R_{N\left(m+l\right)}\right\}\vee \underset{j}{\max }\left\{w_j:R_{N\left(m+j\right)}<R_{N\left(m+l\right)}\right\},$$

$${\overline{w}}_l=\underset{i}{\min }\left\{z_i:R_{N\left(m+l\right)}<R_{Ni}\right\}\wedge \underset{j}{\min }\left\{w_j:R_{N\left(m+l\right)}<R_{N\left(m+j\right)}\right\},$$

for all k, i = 1, …, m; l, j = 1, …, n. The maximum over the empty set is set to −∞, and the minimum over the empty set is set to ∞.

2.4.2. Lemmas.

In order to obtain the posterior distribution and posterior consistency, the following lemmas are needed. The proofs are deferred to the Appendix.

Lemma 1

For any $c_1\in \mathbb{R}$ and c₂ ⩾ 0,

$$\int \overline{\Phi }\left(c_1+c_{2}t\right){\varphi }_{\left(\mu ,\sigma \right)}dt=\overline{\Phi }\left(\frac{c_1+c_2\mu }{\sqrt{1+c_2^2{\sigma }^2}}\right).$$ (9)

Lemma 2

Let S₁, …, S_N be the independent diagnostic variables with underlying disease status D₁, …, D_N, which follow Bin(1, λ). Assume that (2) and (5) hold. Then, we have

$$\text{P}\left(D_i=1|Q_i=t,L_i=2\right)=\text{P}\left(D_i=1|Q_i=t,L_i\ne 2\right)=\frac{\lambda {\varphi }_{\left(\mu ,\sigma \right)}\left(t\right)}{\lambda {\varphi }_{\left(\mu ,\sigma \right)}\left(t\right)+\left(1-\lambda \right)\varphi \left(t\right)},$$ (10)

where L_i is defined in (1).

Remark 1

Lemma 2 implies that D and $\mathbb{1}\{L\ne 2\}$ are independent given the value of Q_i. This independence eliminates dependence on the parameters in the model of verification and makes the calculation much simpler. Further, the expressions are free of g(·), thus allowing us to compute the posterior without actually knowing the verification probability function g(·), as long as it is monotone increasing. In particular, this means that the method is completely protected against misspecification of the verification probability function, which is hard to specify in practice. This is an extremely desirable robustness property of the proposed method.

The following lemma will be used to study the large sample behavior of the posterior distribution but has no role in computing the posterior given a data set.

Lemma 3

Assume that (2) and (5) hold. Then the conditional density of Q is given by

$$f_Q\left(t|L\ne 2\right)=\left(1-{\lambda }_{\left(\mu ,\sigma ,g\right)}^{*}\right){\varphi }_{\left(g\right)}^{*}\left(t\right)+{\lambda }_{\left(\mu ,\sigma ,g\right)}^{*}{\varphi }_{\left(\mu ,\sigma ,g\right)}^{*}\left(t\right),$$ (11)

where ${\lambda }_{\left(\mu ,\sigma ,g\right)}^{*}$ and ${\varphi }_{\left(\mu ,\sigma ,g\right)}^{*}\left(t\right)$ are defined as

$${\lambda }_{\left(\mu ,\sigma ,g\right)}^{*}=\frac{\lambda \int g\left(s\right){\varphi }_{\left(\mu ,\sigma \right)}\left(s\right)ds}{\int g\left(s\right)\left\{\left(1-\lambda \right)\varphi \left(s\right)+\lambda {\varphi }_{\left(\mu ,\sigma \right)}\left(s\right)\right\}ds},$$ (12)

$${\varphi }_{\left(\mu ,\sigma ,g\right)}^{*}\left(t\right)=\frac{g\left(t\right){\varphi }_{\left(\mu ,\sigma \right)}\left(t\right)}{\int g\left(s\right){\varphi }_{\left(\mu ,\sigma \right)}\left(s\right)ds},$$ (13)

and ${\varphi }_{\left(g\right)}^{*}\left(t\right)$ stands for ${\varphi }_{\left(0,1,g\right)}^{*}\left(t\right)$.

Remark 2

When (7) holds, (12) and (13) can be simplified to

$${\lambda }_{\left(\mu ,\sigma ,g\right)}^{*}=\frac{\lambda \Phi \left(\frac{\alpha +\beta \mu }{\sqrt{1+{\left(\beta \sigma \right)}^2}}\right)}{\left(1-\lambda \right)\Phi \left(\frac{\alpha }{\sqrt{1+{\beta }^2}}\right)+\lambda \Phi \left(\frac{\alpha +\beta \mu }{\sqrt{1+{\left(\beta \sigma \right)}^2}}\right)}$$ (14)

$${\varphi }_{\left(\mu ,\sigma ,g\right)}^{*}\left(t\right)={\varphi }_{\left(\mu ,\sigma ,\alpha ,\beta \right)}^{*}\left(t\right)=\frac{\Phi \left(\alpha +\beta t\right){\varphi }_{\left(\mu ,\sigma \right)}\left(t\right)}{\Phi \left(\frac{\alpha +\beta \mu }{\sqrt{1+{\left(\beta \sigma \right)}^2}}\right)}.$$ (15)

2.4.3. Likelihood and posterior distribution.

Based on the invariant set (8), a rank-based partial likelihood under the gold standard can be constructed from

$$\text{P}\left\{\left(\mathit{Z},\mathit{W}\right)\in {\mathcal{D}}_{\text{obs}}|\mu ,\sigma \right\}=\text{P}\left\{\left(\mathit{z},\mathit{w}\right)\in {\mathbb{R}}^{m+n}:R\left(\mathit{z},\mathit{w}\right)=R\left(\mathit{S}\right),L\left(\mathit{z},\mathit{w}\right)=L\left(\mathit{S}\right)|\mu ,\sigma \right\}.$$ (16)

In the presence of the verification bias, the posterior distribution of (λ, μ, σ), given the ranks and the observed labels, is complicated. However, by applying a data augmentation technique, we can implement Gibbs sampling to compute the posterior distribution. More specifically, augmentation variables $\tilde{\mathit{Q}}$, D_un will be used. The resulting posterior distributions of one parameter conditional on the rest of the parameters, ranks, and observed labels are relatively simple and can be described as follows:

• Posterior distribution of (μ, σ) given the rest:

  $$\begin{gathered} {\sigma }^2|\text{rest}\sim \text{inverse gamma}\left(\left(n^{\prime }-1\right)/2,\left(n^{\prime }-1\right)s_w^2/2\right) \\ \mu |\text{rest}\sim \text{TN}\left({\overline{W}}_{n^{\prime }},{\sigma }^{\prime }/n^{\prime },\left(0,\infty \right)\right), \end{gathered}$$ (17)

  where $n^{\prime }={\sum }_{i=1}^N\left\{\mathbb{1}\left({\tilde{D}}_i=1,{\tilde{L}}_i=2\right)+\mathbb{1}\left({\tilde{L}}_i=1\right)\right\}$, $s_w^2={\sum }_{j=1}^{n^{\prime }}{\left(W_j-{\overline{W}}_{n^{\prime }}\right)}^2/\left(n^{\prime }-1\right)$, and ${\overline{W}}_{n^{\prime }}={\sum }_{j=1}^{n^{\prime }}{W}_j/n^{\prime }$.
• $\tilde{\mathit{Q}}$ can be sequentially updated conditional on (μ, σ) by

  $${\tilde{Q}}_i^{\left(new\right)}|\text{rest}\sim \{\begin{array}{cc}\text{TN}\left(0,1,\left({\tilde{Q}}_{i-1}^{\left(\text{new}\right)},{\tilde{Q}}_{i+1}\right)\right),& \text{if}{\tilde{D}}_i=0,\\ \text{TN}\left(\mu ,{\sigma }^2,\left({\tilde{Q}}_{i-1}^{\left(\text{new}\right)},{\tilde{Q}}_{i+1}\right)\right),& \text{if}{\tilde{D}}_i=1,\end{array}$$ (18)

  where i = 1, …, N, ${\tilde{Q}}_0=-\infty$, ${\tilde{Q}}_{N+1}=\infty$.
• Posterior distribution of λ given the rest:

  $$\lambda |\text{rest}\sim \text{Beta}\left(l_1+n^{\prime },l_0+m^{\prime }\right),$$ (19)

  where $m^{\prime }={\sum }_{i=1}^N\left\{\mathbb{1}\left({\tilde{D}}_i=0,{\tilde{L}}_i=2\right)+\mathbb{1}\left({\tilde{L}}_i=0\right)\right\}$.
• Update the augmentation variable ${\tilde{D}}_i\in {\mathit{D}}_{\text{un}}$ by

  $${\tilde{D}}_i^{\left(\text{new}\right)}|\text{rest}\stackrel{\text{ind}}{\sim }\text{Bin}\left(1,\frac{\lambda {\varphi }_{\left(\mu ,\sigma \right)}\left({\tilde{Q}}_i^{\left(\text{new}\right)}\right)}{\lambda {\varphi }_{\left(\mu ,\sigma \right)}\left({\tilde{Q}}_i^{\left(\text{new}\right)}\right)+\left(1-\lambda \right)\varphi \left({\tilde{Q}}_i^{\left(\text{new}\right)}\right)}\right),$$ (20)

The posterior mean of (μ, σ) was used as the Bayes estimator in the BRL method. In this paper, the posterior median is used in place of posterior mean, primarily because the posterior distribution is often considerably skewed.

2.5. Computational algorithm

By applying a data augmentation technique, we can implement Gibbs sampling to obtain posterior median of ${\pi }^{*}\left(\tilde{\mathit{Q}},\mu ,\sigma ,\lambda ,{\mathit{D}}_{\text{un}}|\mathit{S},\mathit{L}\right)$. Gibbs sampling procedure can be described as follows:

1. Choose an initial value of (μ, σ). Generate any initial value of (Q₁, …, Q_N), which lies in ${\mathcal{D}}_{\mathrm{obs}}$, in particular, a sample from the product m* many N(0,1) and n* many N(μ, σ), where m* and n* are the number of observations having labels from healthy and diseased groups, N* = m* + n*, and restricting the product measure in D_obs. Then, initialize missing labels by a (N - N*) independent Bin(1, p₀) variables, where p₀ = l₁/(l₁ + l₀).

2. Start the iterations:

   1. Conditional on (μ, σ), update $\tilde{\mathit{Q}}$, denoted as ${\tilde{\mathit{Q}}}^{\left(\text{new}\right)}$ with constraint $\left(\mathit{Z},\mathit{W}\right)\in {\mathcal{D}}_{\text{obs}}$ by following (18).
   2. Update Z and W values based on ${\tilde{\mathit{Q}}}^{\left(\text{new}\right)}$ and $\tilde{\mathit{D}}$.
   3. By following the posterior distributions specified in Section 2.4.3, update (μ, σ, λ, D_un).

3. After the burn-in period, we obtain the estimates â and $\widehat{b}$ of the intercept a and the slope b in (3), respectively, by picking up the median of the sampled values of μ/σ and 1/σ, respectively. We can also calculate the 100(1 – γ)% credible interval for a as (q_a,γ/2,q_a,1−γ/2), where q_a,γ/2 and q_a,1−γ/2 denote γ/2 and 1 – γ/2 quantiles of the sampled values of a. The credible interval of (q_b,γ/2,q_b,1−γ/2) for b is similarly defined. We also compute the estimate of AUC and its 100(1 – γ)% credible interval.

3. Consistency of the posterior

Let (μ₀, σ₀) be the true value of (μ, σ). Consider a joint prior density π on (μ, σ) with respect to the Lebesgue measure (denoted by ν). We shall show the posterior distribution Π(·|R(S), L for (μ, σ) is consistent at (μ₀, σ₀), that is, the posterior distribution concentrates around (μ₀, σ₀) as the sample size increases to infinity; see [18].

Theorem 1

Assume (2) and (5) hold, where the function g is a monotone increasing functions from $\mathbb{R}$ to (0, 1), and that π(μ, σ) > 0 a.e. [ν] over $\mathbb{R}\times {\mathbb{R}}^{+}$. Then for any neighborhood ${\mathcal{U}}_0$ of (μ₀, σ₀), we have that

$$\underset{N\to \infty }{\lim }\Pi \left(\left(\mu ,\sigma \right)\in {\mathcal{U}}_0\backslash R\left(\mathit{S}\right),\mathit{L}\right)=1\text{a.s.}\left[P_{{\mu }_0,{\sigma }_0,g,H}^{\infty }\right],$$ (21)

for (μ₀, σ₀) a.e. [ν], where $P_{{\mu }_0,{\sigma }_0,g,H}^{\infty }$ denotes the true joint distribution of all observations described by (2) and (5).

Since imputation of missing labels is the only additional step in the PG-BRL method compared to the BRL method, we shall first sketch the proof of the consistency of the posterior distribution of the binormal parameters (μ, σ) for the BRL method, and then point out the difference with the present PG-BRL situation.

The main idea behind the proof of posterior consistency for the BRL or PG-BRL method is based on a very general posterior consistency theorem due to Doob. This theorem applies to any type of data, provided it can be shown that the parameter is expressible as a function of the whole sequence of observations (see Theorem 2 in the Appendix). For a rank-based method such as BRL, this was shown by essentially two major steps in Gu and Ghosal [17]. First, one shows that the ‘quantile of an observation in the whole mixed population’ U_i, as defined in equation (5) of Gu and Ghosal [17], is retrievable from the information of only the relative ranks and the labels at each stage of the asymptotics. Then one finds a consistent estimator of the binormal parameters based on these U_j’s and the label information. This shows that the binormal parameters can be expressed as functions of ranks and the labels corresponding to all stages. Now in the PG-BRL method, we need to work with observations with verified labels only, which makes the population distribution different from that of all observations. This leads to a different notion of ‘population quantile of an observation’ U_j as defined by (A.1) in the Appendix. These U_js can be retrieved from all ranks and verified labels information in the same way as before. However, the distribution of the U_js given the labels are different in this situation and will depend on the verification function g in (5). This would be possible whenever the family of distributions of U_j corresponding to verified disease status is identifiable. The identifiability condition will hold if no two functions in the family $\mathcal{G}$ are such that their ratio is the exponential of a quadratic function. The condition is very mild—it is satisfied by (6), (7) and most conceivable verification mechanisms.

4. Simulation studies

Lemma 2 implies that within an MCMC iteration, updating of D_un will depend on (λ, μ, σ, Q) only. Thus, none of the parameters in model (5) matter in the MCMC scheme, and hence they could be ignored from a computational point of view. This makes our PG-BRL estimate much simpler to calculate without a specified form of g in model (5). In this section, we intend to show that verification bias-corrected estimators have less bias and variability than, or are comparable with other well-known methods called semiparametric efficient estimator using the estimated verification probabilities (SPE-E), SPE-E curve adjusted by isotonic regression (SPE-E-A), full imputation (FI), mean score imputation (MSI), and inverse probability weighting (IPW) estimators proposed by Alonzo and Pepe [10].

4.1. Under the bionormality assumption

Sets of simulations letting true AUC equal to 0.65, 0.75, and 0.85, respectively, are conducted to compare their estimates of the AUC under different forms of g in model (5), different sample sizes based on 1000 simulated data sets. Within each simulated data setting, two missing mechanisms based on verification models (7) for probit regression and (6) for threshold value, are used to generate the partial gold standard data. In the former case, we fix β = 0.3, and use the values α = −0.43 for AUC = 0.65, α = −0.48 for AUC = 0.75, α = −0.53 for AUC = 0.85. In the latter case, and p₁ = 0.8 and p₂ = 0.2 in (6). All these given on an average 36% of the subjects having the labels. The PG-BRL estimates are obtained by 100,000 Gibbs samples after burn-in at 5000 for each replication. For each replication, there are total 100 and 200 subjects whose diagnostic test results are generated from N(0,1) and $\text{N}\left(\sqrt{1+{\sigma }^2}{\Phi }^{-1}\left(\text{AUC}\right),{\sigma }^2\right)$ (4) with a disease prevalence rate 0.25, where σ is equal to 1.5 for all cases. Thus, for AUC = 0.85, the true values of a and b are 1.2457 and 0.6667, respectively; for AUC = 0.75, the true values of a and b are 0.8107 and 0.6667, respectively; for AUC = 0.65, the true values of a and b are 0.4631 and 0.6667, respectively. We compare our proposed PG-BRL method with SPE-E, PI, MSI, and IPW methods in terms of accuracy.

From Table I, where the data labels are generated by (7) and (6), respectively, we can see that PG-BRL performs consistently better in term of accuracy in most of the cases when the true AUC is moderate among these five methods. When the AUC is equal to 0.75, which is often considered to be a very realistic value in practical situations, PG-BRL clearly is more accurate than the other methods. However, when AUC goes down to 0.65, SPE-E, SPE-E-A, and IPW methods are less biased than PG-BRL, PI, and MSI methods. Comparing mean squared error (MSE), PG-BRL method does have the smallest value among all methods. The estimates of (a, b), which are available only for the PG-BRL method, are shown in Table II. The accuracy of PG-BRL estimates in Table II varies for different verification functions but improves with more samples. Theorem 1 implies accuracy of estimates with sufficient amount of data under various verification functions.

Table I.

Simulation studies: estimates of AUC using methods PG-BRL, SPE-E, SPE-E-A, FI, MSI, and IPW.

Imputation		N = 100		N = 200
Model	Method	Bias	MSE	Bias	MSE
Probit	PG-BRL	−0.0321	0.0085	−0.0156	0.0046
AUC=0.85	SPE-E	0.0162	0.0066	0.0136	0.0036
	SPE-E-A	0.0156	0.0065	0.0135	0.0036
	FI	0.0357	0.0050	0.0349	0.0032
	MSI	0.0309	0.0050	0.0303	0.0031
	IPW	−0.0349	0.0100	−0.0357	0.0060
Probit	PG-BRL	0.0155	0.0068	0.0084	0.0043
AUC=0.75	SPE-E	0.0339	0.0126	0.0208	0.0062
	SPE-E-A	0.0335	0.0125	0.0207	0.0062
	FI	0.0624	0.0113	0.0535	0.0065
	MSI	0.0559	0.0111	0.0465	0.0060
	IPW	−0.0188	0.0137	−0.0312	0.0078
Probit	PG-BRL	0.0622	0.0083	0.0529	0.0059
AUC=0.65	SPE-E	0.0360	0.0164	0.0343	0.0093
	SPE-E-A	0.0358	0.0164	0.0343	0.0093
	FI	0.0729	0.0168	0.0725	0.0109
	MSI	0.0647	0.0160	0.0644	0.0100
	IPW	−0.0130	0.0154	−0.0117	0.0082
Threshold	PG-BRL	−0.0067	0.0078	0.0013	0.0038
AUC=0.85	SPE-E	0.0144	0.0098	0.0110	0.0045
	SPE-E-A	0.0129	0.0096	0.0104	0.0044
	FI	0.0391	0.0060	0.0383	0.0035
	MSI	0.0329	0.0059	0.0330	0.0033
	IPW	0.0068	0.0100	0.0078	0.0046
Threshold	PG-BRL	0.0220	0.0077	0.0146	0.0052
AUC=0.75	SPE-E	0.0213	0.0146	0.0120	0.0077
	SPE-E-A	0.0199	0.0143	0.0116	0.0076
	FI	0.0595	0.0107	0.0572	0.0073
	MSI	0.0517	0.0103	0.0493	0.0067
	IPW	0.0098	0.0151	0.0055	0.0078
Threshold	PG-BRL	0.0687	0.0105	0.0482	0.0053
AUC=0.65	SPE-E	0.0245	0.0203	0.0182	0.0091
	SPE-E-A	0.0233	0.0199	0.0180	0.0090
	FI	0.0744	0.0167	0.0729	0.0104
	MSI	0.0645	0.0159	0.0634	0.0094
	IPW	0.0114	0.0206	0.0103	0.0090

Table II.

Simulation studies: estimates of a and b using method PG-BRL.

Imputation		N = 100		N = 200
Model	Method	Bias	MSE	Bias	MSE
Probit	PG-BRL a	0.0134	0.4438	0.0121	0.2236
AUC=0.85	b	0.0044	0.0846	−0.0080	0.0442
Probit	PG-BRL a	0.1764	0.3247	0.0844	0.1314
AUC=0.75	b	0.0206	0.0794	0.0063	0.0331
Probit	PG-BRL a	0.2792	0.2179	0.2209	0.1209
AUC=0.65	b	0.0253	0.0714	0.0409	0.0332
Threshold	PG-BRL a	0.2420	0.6750	0.1483	0.3226
AUC=0.85	b	0.0955	0.1097	0.0506	0.0535
Threshold	PG-BRL a	0.2409	0.4305	0.1316	0.1905
AUC=0.75	b	0.0667	0.0927	0.0310	0.0373
Threshold	PG-BRL a	0.3382	0.3463	0.1995	0.1046
AUC=0.65	b	0.0684	0.0833	0.0373	0.0268

4.2. Departure from the bionormality assumption

Because our method is based on the binormality assumption, it is important to study the effect of departure from binormality. We generate (X₁, …, X_m) independently from beta distribution with mean 0.15 and standard deviation 0.15, (Y₁, …, Y_n) independently from beta distribution with mean 0.25 and standard deviation 0.15, where m = 50, n = 150. The corresponding AUC is equal to 0.715, and 1000 simulated data sets are used in the study. For the parameters in the verification models, we use α = −0.40, β = 0.3 for model (7), and p₁ = 0.8, p₂ = 0.2 for model (6) to make on an average 36% of the subjects having the labels. The PG-BRL estimates are obtained by 100,000 Gibbs samples after burn-in at 5000 for each replication. From the results shown in Table III, we can see that even though the PG-BRL estimator has higher bias than SPE-E and IPW estimators, but its MSE is much smaller. The simulation results show that our procedure has reasonable robustness properties against departure from binormality.

Table III.

Simulation studies (Departure from binormality assumption): estimates of AUC using methods PG-BRL, SPE-E, SPE-E-A, FI, MSI, IPW.

Imputation		N = 200
Model	Method	Bias	MSE
Probit	PG-BRL	0.0257	0.0022
AUC=0.715	SPE-E	0.0070	0.0040
	SPE-E-A	0.0055	0.0040
	FI	−0.0560	0.0076
	MSI	−0.0381	0.0055
	IPW	0.0066	0.0042
Threshold	PG-BRL	0.0268	0.0026
AUC=0.715	SPE-E	0.0063	0.0057
	SPE-E-A	0.0017	0.0052
	FI	−0.0930	0.0125
	MSI	−0.0746	0.0093
	IPW	0.0041	0.0055

4.3. Departure from missing at random assumption

When MAR assumption does not hold, the dependence of the verification probability in (5) on disease status will make the probabilities in (10) different and dependent on the functional form of g in (5). More precisely, let

$$\text{P}\left(L_i\ne 2|Q_i,D_i=0\right)=g_0\left(Q_i\right),$$ (22)

$$\text{P}\left(L_i\ne 2|Q_i,D_i=1\right)=g_1\left(Q_i\right),$$ (23)

then proceeding as in the proof of Lemma 2, it follows that

$$\text{P}\left(D_i=1|Q_i=t,L_i=2\right)=\frac{\lambda g_1\left(t\right){\varphi }_{\left(\mu ,\sigma \right)}\left(t\right)}{\lambda g_1\left(t\right){\varphi }_{\left(\mu ,\sigma \right)}\left(t\right)+\left(1-\lambda \right)g_0\left(t\right)\varphi \left(t\right)}.$$ (24)

Here, we illustrate a case non-MAR (NMAR) where the MAR assumption fails. Assume P(D = 1) = 0.25. To achieve 36% verification, that is, P(L_i ≠ 2) = 0.36, we can choose P(L_i ≠ 2 | D = 1) = 0.80 and hence will need to set P(L_i ≠ 2 | D = 0) = 0.213. Let g₀(t) = Φ(α₀ + β₀t), and g₁(t) = Φ(α₁ + β₁t). We wish to choose pairs (α₀, β₀) ≠ (α₁, β₁) (i.e., NMAR), which will yield verification probabilities 0.80 and 0.213 under disease and non-disease situations, respectively. To this end, use Lemma 1 with β₀ = β₁ = 0.3 and solve the following equations:

$$\Phi \left(\frac{{\alpha }_1+{\beta }_1\mu }{\sqrt{1+{\beta }_1^2{\sigma }^2}}\right)=0.8,\Phi \left(\frac{{\alpha }_0}{\sqrt{1+{\beta }_0^2}}\right)=0.213,$$

given α₀ = −0.831 and α₁ = 0.558, when the actual values of μ and σ are 1.216 and 1.5, respectively.

We compare estimates shown in Table IV by NMAR with MAR imputed by threshold model, where simulation setting for MAR exactly follows Section 4.1 with true AUC equal to 0.75. We observe that even under departure from the MAR assumption, the proposed PG-BRL method leads to smaller MSE compared with other methods.

Table IV.

Simulation studies (Departure from MAR assumption): estimates of AUC using methods PG-BRL, SPE-E, SPE-E-A, FI, MSI, IPW.

Assumption		N = 200
Model	Method	Bias(True AUC=0.75)	MSE
MAR	PG-BRL	0.0146	0.0052
Threshold	SPE-E	0.0120	0.0077
	SPE-E-A	0.0116	0.0076
	FI	0.0572	0.0073
	MSI	0.0493	0.0067
	IPW	0.0055	0.0078
NMAR	PG-BRL	−0.0569	0.0052
	SPE-E	−0.0855	0.0126
	SPE-E-A	−0.0855	0.0126
	FI	−0.0408	0.0050
	MSI	−0.0479	0.0058
	IPW	−0.1184	0.0188

5. Real data analysis

One common issue with ROC curves and biopsy verification occurs whenever biopsy results are used as the gold standard for other measurements, usually with respect to fibrosis or steatosis. The biopsy may not be representative of the liver as a whole, and there is always interpretation noise (inter and intra-observer variability). The clinical test may not be a perfect match for the histological observation. However, to explore the relationship between the specified liver enzyme test and the degree of cholestasis in drug-induced liver injury (DILI), liver biopsy database is still helpful. Here, the specified liver enzyme tests include serum total bilirubin (STB) level and alkaline phosphatase value (AKP). Because the bilirubin may rise without the accumulation of visible bile in the liver, there is not a perfect match between the serum bilirubin and the biopsy. Nevertheless, the biopsy still gives precise information about the degree of cholestasis.

We shall use the data from DILI network (DILIN). The DILIN, sponsored by the National Institutes of Health in 2003, is a consortium of a data coordinating center, five academic medical centers later expanded to nine starting from the renewal of the second 5-year grant. The DILIN prospective study is an ongoing observational study of over 1000 patients with suspected liver injury due to various drugs and complementary and alternative medications. The goals of this study include the earliest recognition of DILI, the development of standardized instruments and terminology to help identify cases of DILI, and investigating clinical and genetic risk factors that predict DILI. The study design and development of the prospective study, and the process of causality assessment, were presented by Fontana et al. [19], and Rockey et al. [20], respectively.

Up to January 2011, there were 898 subjects enrolled in DILIN prospective study. Among these subjects, we include 405 subjects in this study, who had STB and AKP values at DILI first abnormal date (DILI onset date) and had causality score either definitely, very likely, or probably adjudicated by DILIN causality committee. The subjects follow up on the sixth month after their baseline visits. The biopsy samples were restricted to either baseline or historical biopsy samples collected within 60 days of DILI onset and closest to DILI onset for multiple biopsy data. We dichotomize the degree of cholestasis into 0–1 or 2–3 to reduce intra-observer variability, where 80 subjects (56%) had no disease, and 64 subjects (44%) had disease. The STB or AKP values were chosen to be closest to the biopsy date with a time window of 7 days. If not, then the corresponding lab value at onset was used instead. Because only 144 subjects out of 405 had biopsy results, verification bias may occur if the analysis is just based on these 144 subjects with the degree of cholestasis. Hence, verification bias-correction methods are needed in this content. By using PG-BRL and other methods listed in the simulation study, we have the following results for STB and AKP in Table V and Figure 1.

Table V.

Real data setting: estimates of AUCs and corresponding 95% confidence intervals (CI) for total bilirubin and alkaline phosphatase.

Lab Test	Method	$\widehat{\mathrm{AUC}}(\widehat{\mathrm{sd}})$	95% CI
STB	PG-BRL	0.7388 (0.0559)	(0.6389, 0.8601)
	SPE-E	0.7198 (0.0655)	(0.5970, 0.8495)
	SPE-E-A	0.7109 (0.0573)	(0.5938, 0.8145)
	FI	0.6704 (0.0357)	(0.6055, 0.7337)
	MSI	0.7041 (0.0417)	(0.6201, 0.7849)
	IPW	0.6714 (0.0481)	(0.5790, 0.7643)
AKP	PG-BRL	0.6550 (0.0738)	(0.5624, 0.8527)
	SPE-E	0.6283 (0.0962)	(0.4421, 0.8183)
	SPE-E-A	0.6248 (0.0865)	(0.4517, 0.7727)
	FI	0.5683 (0.0289)	(0.5156, 0.6353)
	MSI	0.5953 (0.0447)	(0.5036, 0.6788)
	IPW	0.5768 (0.0498)	(0.4693, 0.6716)

Figure 1.

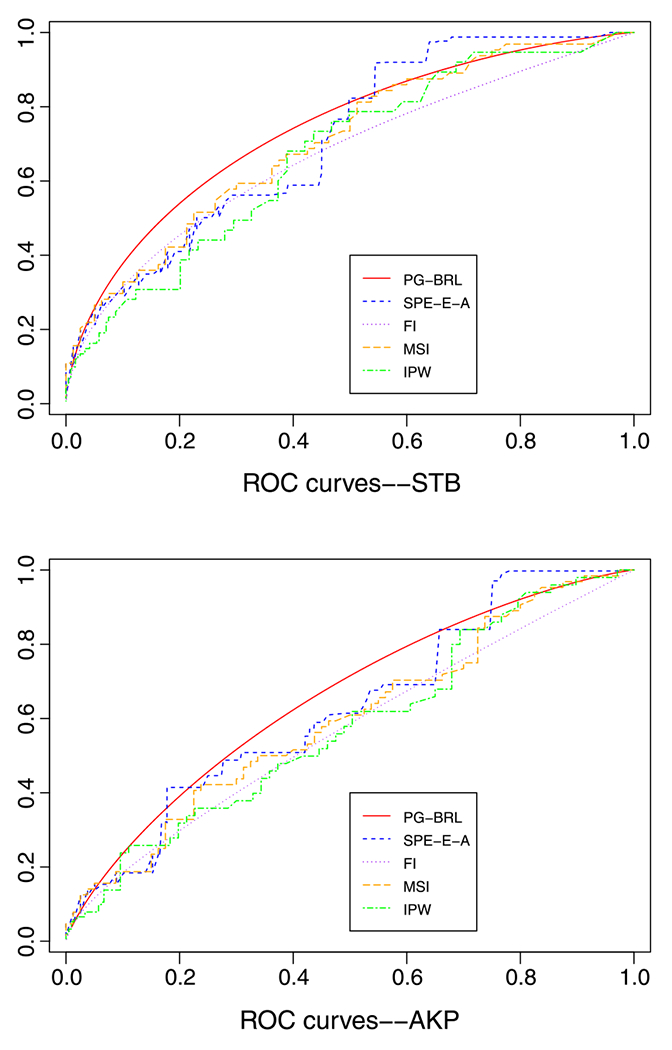
Real data analysis: ROC curve estimates for serum total bilirubin and alkaline phosphatase.

We obtain point-estimates of the AUC using the proposed PG-BRL method based on the measurements STB and AKP, which are given by 0.7388 and 0.6550. This seems to indicate that categorization of degree of cholestatis based on STB is more accurate than that based on AKP. A formal comparison of the accuracies of these two diagnostic measurements will have to involve a test of hypothesis of the equality of the two AUC values, which will necessarily involve a joint modeling of both STB and AKP for each subject. This will allow us to draw MCMC sample from the joint posterior distribution of all parameters in the two binormal models for STB and AKP, and consequently from the posterior distribution of the difference or ratio of the corresponding AUC. Presently, such a joint binormal model has not been developed, so we refrain from such an analysis.

Although SPE-E estimator is ‘doubly robust’, ensuring either verification model or disease model can be challenging. A difficulty with the SPE-E method is that the estimated ROC curve may not be monotone due to negative component in the formula of estimates of TPR(c) and FPR(c). Hence, SPE-E-A ROC curve is displayed in Figure 1 instead of SPE-E ROC curve.

For all the other approaches, we used to compare with our method, it is difficult to know or estimate S_(p1N) in (6), because two populations of AKP values are well mixed. Thus, we conclude that PG-BRL method is more flexible when the disease and non-disease population are well mixed, and no hyperparameters are needed in its calculation.

6. Discussion

In this paper, we considered modeling the diagnostic variable as an independent variable in the binormal model. Sometimes a set of covariates, say V, is also observed, which contributes a linear effect through an unknown regression coefficient β, that is, the binormal model will become

$$H\left(X_i-{\mathit{\beta }}^T{\mathit{V}}_i\right)|D_i=0\stackrel{\text{i.i.d.}}{\sim }\text{N}\left(0,1\right),$$

$$H\left(Y_i-{\mathit{\beta }}^T{\mathit{V}}_i\right)|D_i=1\stackrel{\text{i.i.d.}}{\sim }\text{N}\left(\mu ,{\sigma }^2\right).$$

In this case, the BRL and the PG-BRL methods are not applicable because the ranks of the covariate adjusted observations may change between MCMC iterations due to the changes in the sampled value of β. This will destroy the invariance structure that the rank-likelihood is based on. In order to accommodate covariates in the BRL and PG-BRL methods, we can adopt a preprocessing step to replace the diagnostic test values with the residuals after adjusting for the covariates using a regression model and estimating the regression coefficient by the method of least squares. If a handful of covariates among several needs to be selected as well, then the LASSO estimator may be used in place of the least square estimator. Of course, a fully Bayesian analysis is possible by using the full likelihood instead of the rank-likelihood, but that will need a prior on the transformation H as well.

In a clinical practice, sometimes the MAR assumption may be violated. For instance, when a patient is too sick or old, or is unable to bear the cost of the gold standard test, he or she may not be able to follow the physician’s recommendation to take the gold standard test. In these cases, probability of verification will depend on covariates and disease status as well unless all the relevant health and financial information are collected also, and are properly accounted in the model (5) for verification. The PG-BRL is nevertheless applicable, but the posterior will depend on the verification functions g₀ and g₁ in (22) and (23), respectively, which will have to be explicitly known.

Appendix

Proof of Lemma 1

The result is well known, but we give a proof for completeness. First, we can show that

$$\int \stackrel{\_}{\Phi }\left(c_1+c_{2}t\right)\varphi \left(t\right)dt=\stackrel{\_}{\Phi }\left(\frac{c_1}{\sqrt{1+c_2^2}}\right).$$

Let $J\left(c_1\right)=\int \stackrel{\_}{\Phi }\left(c_1+c_{2}t\right)\varphi \left(t\right)dt$. Then, by differentiation under the integral sign which can be justified by the dominated convergence theorem,

$$\begin{gathered} J^{\prime }\left(c_1\right)=-\int \Phi \left(c_1+c_{2}t\right)\varphi \left(t\right)dt \\ =-\int \frac{1}{2\pi }\exp \left\{-\frac{1}{2}\left(c_1^2+2c_1{c}_{2}t+c_2^2{t}^2+t^2\right)\right\}dt \\ =-\frac{1}{\sqrt{2\pi }}\exp \left\{-\frac{c_1^2}{2\left(1+c_2^2\right)}\right\}\int \frac{1}{\sqrt{2\pi }}\exp \left\{-\frac{1}{2}{\left(u+w\right)}^2\right\}\frac{du}{\sqrt{1+c_2^2}} \\ =-\varphi \left(\frac{c_1}{\sqrt{1+c_2^2}}\right)\frac{1}{\sqrt{1+c_2^2}}, \end{gathered}$$

where we have used the substitution $u=t\sqrt{1+c_2^2}$, $w=c_1{c}_2/\sqrt{1+c_2^2}$. Hence, $J\left(c_1\right)=-\Phi \left(c_1/\sqrt{1+c_2^2}\right)+c$, for some constant c. Because J(∞) = 0, we have c = 1, and hence $J\left(c_1\right)=1-\Phi \left(c_1/\sqrt{1+c_2^2}\right)=\Phi \left(c_1/\sqrt{1+c_2^2}\right)$.

Now letting $s=\frac{t-\mu }{\sigma }$, we have

$$\int \stackrel{\_}{\Phi }\left(c_1+c_{2}t\right){\varphi }_{\left(\mu ,\sigma \right)}dt=\int \stackrel{\_}{\Phi }\left(c_1+c_2\mu +c_2\sigma s\right){\varphi }_{(}s)ds=\stackrel{\_}{\Phi }\left(\frac{c_1+c_2\mu }{\sqrt{1+c_2^2{\sigma }^2}}\right).$$

Proof of Lemma 2

By Bayes’ theorem, we have

$$\text{P}\left(D_i=1|Q_i=t,L_i=2\right)=\frac{\text{P}\left(D_i=1\right)f_{Q_i}\left(t|D_i=1\right)\text{P}\left(L_i=2|Q_i=t,D_i=1\right)}{{\sum }_{d=0}^1\left\{\text{P}\left(D_i=d\right)f_{Q_i}\left(t|D_i=d\right)\text{P}\left(L_i=2|Q_i=t,D_i=d\right)\right\}}$$

Because f_Qi(t | D_i = 1, L_i = 2) = f_Qi(t | D_i = 1) and P(L_i = 2 | Q_i = t, D_i = 1) = P(L_i = 2 | Q_i = t, D_i = 0) = 1 − g(t), we have

$$\begin{gathered} \text{P}\left(D_i=1|Q_i=t,L_i=2\right)=\frac{\lambda {\varphi }_{\left(\mu ,\sigma \right)}\left(t\right)\left(1-g\left(t\right)\right)}{\lambda {\varphi }_{\left(\mu ,\sigma \right)}\left(t\right)\left(1-g\left(t\right)\right)+\left(1-\lambda \right)\varphi \left(t\right)\left(1-g\left(t\right)\right)} \\ =\frac{\lambda {\varphi }_{\left(\mu ,\sigma \right)}\left(t\right)}{\lambda {\varphi }_{\left(\mu ,\sigma \right)}\left(t\right)+\left(1-\lambda \right)\varphi \left(t\right)}, \end{gathered}$$

and P(L_i = 2) = ∫ P(L_i = 2 | Q_i = t)f_Qi(t)dt = ∫(1 − g(t)){λϕ_(μ,σ)(t) + (1 − λ)ϕ(t)}dt.

By following the same lines, we have

$$\begin{gathered} \text{P}\left(D_i=1|Q_i=t,L_i\ne 2\right)=\frac{\lambda {\varphi }_{\left(\mu ,\sigma \right)}\left(t\right)g\left(t\right)}{\lambda {\varphi }_{\left(\mu ,\sigma \right)}\left(t\right)g\left(t\right)+\left(1-\lambda \right)\varphi \left(t\right)g\left(t\right)} \\ =\frac{\lambda {\varphi }_{\left(\mu ,\sigma \right)}\left(t\right)}{\lambda {\varphi }_{\left(\mu ,\sigma \right)}\left(t\right)+\left(1-\lambda \right)\varphi \left(t\right)}, \end{gathered}$$

and P(L_i ≠ 2) = ∫P(L_i ≠ 2 | Q_i = t)f_Qi(t)dt = ∫ g(t){λϕ_(μ,σ)(t) + (1 − λ)ϕ(t)} dt.

Proof of Lemma 3

By Bayes’ theorem, we have

$$\begin{gathered} f_Q\left(t|L\ne 2\right)=\frac{\text{P}\left(L=0\text{or}1|Q=t\right)f_Q\left(t\right)}{\int \text{P}\left(L=0\text{or}1|Q=s\right)f_Q\left(s\right)ds} \\ =\frac{g\left(t\right)\left\{\left(1-\lambda \right)\varphi \left(t\right)+\lambda {\varphi }_{\left(\mu ,\sigma \right)}\left(t\right)\right\}}{\int g\left(s\right)\left\{\left(1-\lambda \right)\varphi \left(s\right)+\lambda {\varphi }_{\left(\mu ,\sigma \right)}\left(s\right)\right\}ds} \\ =\frac{g\left(t\right)\varphi \left(t\right)}{\int g\left(s\right)\varphi \left(s\right)ds}\times \frac{\left(1-\lambda \right)\int g\left(s\right)\varphi \left(s\right)ds}{\int g\left(s\right)\left\{\left(1-\lambda \right)\varphi \left(s\right)+\lambda {\varphi }_{\left(\mu ,\sigma \right)}\left(s\right)\right\}ds}+\frac{g\left(t\right){\varphi }_{\left(u,\sigma \right)}\left(t\right)}{\int g\left(s\right){\varphi }_{\left(u,\sigma \right)}\left(s\right)ds}\times \frac{\lambda \int g\left(s\right){\varphi }_{\left(u,\sigma \right)}\left(s\right)ds}{\int g\left(s\right)\left\{\left(1-\lambda \right)\varphi \left(s\right)+\lambda {\varphi }_{\left(\mu ,\sigma \right)}\left(s\right)\right\}ds} \\ =\left(1-{\lambda }_{\left(\mu ,\sigma ,g\right)}^{*}\right){\varphi }_{\left(g\right)}^{*}\left(t\right)+{\lambda }_{\left(\mu ,\sigma ,g\right)}^{*}{\varphi }_{\left(\mu ,\sigma ,g\right)}^{*}\left(t\right), \end{gathered}$$

where ${\lambda }_{\left(\mu ,\sigma ,g\right)}^{*}$ and ${\varphi }_{\left(\mu ,\sigma ,g\right)}^{*}\left(t\right)$ are defined in (12) and (13), respectively.

The following version of a well-known theorem by Doob’s theorem was used, whose proof can be found in Ghosal and Van der Vaart [21].

Theorem 2 (Doob’s Theorem)

Let X⁽ⁿ⁾ be observations whose distribution depends on a parameter θ, and both X⁽ⁿ⁾ and θ take values in Polish spaces. Let Π be a prior distribution on θ. Assume that θ is equivalent to a measurable function f on (X⁽ⁿ⁾ : n ⩾ 1), that is, θ = f(X⁽ⁿ⁾ : n ⩾ 1) a.s. with respect to the joint distribution of θ and (X⁽ⁿ⁾ : n ⩾ 1). Then the posterior Π(·|X⁽ⁿ⁾) is strongly consistent at θ for almost every θ [Π].

Proof of Theorem 1

Because the posterior distribution of (μ, σ) given the ranks and labels do not depend on g and H, we may treat them as known for the purpose of theoretically studying consistency of the posterior distribution of (μ, σ), even though g and H need not be actually known.

Let Ω_N stand for a set of all permutations of {1, …, N}. If we can show that there exists a function $h^{*}:{\Omega }_1\times {\Omega }_2\times \dots \times {\left\{0,1,2\right\}}^{\infty }\to \mathbb{R}\times {\mathbb{R}}^{+}\times \mathbb{R}\times {\mathbb{R}}^{+}$, such that (μ, σ) = h*(R_N, N ⩾ 1, (L₁, L₂, …)), then by applying Doob’s Theorem, (21) holds.

Let 1 ⩽ i₁ < ⋯ < i_N* ⩽ N be the collection of indices for which L_ij = 0 or 1, and j = 1, …, N*. From Lemma 3, $f_Q\left(t|L_i\ne 2\right)=\left(1-{\lambda }_{\left(\mu ,\sigma ,g\right)}^{*}\right){\varphi }_{\left(g\right)}^{*}\left(t\right)+{\lambda }_{\left(\mu ,\sigma ,g\right)}^{*}{\varphi }_{\left(\mu ,\sigma ,g\right)}^{*}\left(t\right)$, with notations as in Lemma 3. Hence, disregarding the disease status, we can regard the overall sample coming independently from the mixture distribution, that is, $Q_{i_j}\stackrel{\text{i.i.d.}}{\sim }\left(1-{\lambda }_{\left(\mu ,\sigma ,g\right)}^{*}\right){\varphi }_{\left(g\right)}^{*}+{\lambda }_{\left(\mu ,\sigma ,g\right)}^{*}{\varphi }_{\left(\mu ,\sigma ,g\right)}^{*}$, where ${\Phi }_{\left(g\right)}^{*}\left(t\right)$ and ${\Phi }_{\left(\mu ,\sigma ,g\right)}^{*}$ are the CDFs of ${\varphi }_{\left(g\right)}^{*}\left(t\right)$ and ${\varphi }_{\left(\mu ,\sigma ,g\right)}^{*}\left(t\right)$, respectively. Thus, we have

$$U_j=\left\{\left(1-{\lambda }_{\left(\mu ,\sigma ,g\right)}^{*}\right){\Phi }_{\left(g\right)}^{*}+{\lambda }_{\left(\mu ,\sigma ,g\right)}^{*}{\Phi }_{\left(\mu ,\sigma ,g\right)}^{*}\right\}\left(Q_{i_j}\right)\stackrel{\text{i.i.d.}}{\sim }\text{Uniform(0, 1)}.$$ (A.1)

Let $\left({R^{\prime }}_{N^{*}1},\dots ,{R^{\prime }}_{N^{*}{N}^{*}}\right)$ be the rank vector of (U₁, …, U_N*), and $\left({L^{\prime }}_{N^{*}1},\dots ,{L^{\prime }}_{N^{*}{N}^{*}}\right)$ stand for their labels. Now, as in Theorem a on page 157 of Hájek and šidák [22], we have

$$\begin{gathered} \text{E}\left(U_j-\frac{{R^{\prime }}_{N^{*}{i}_j}}{N^{*}+1}\right)=\frac{1}{N^{*}}\sum _{k=1}^{N^{*}}E\left[{\left(U_j-\frac{k}{N^{*}+1}\right)}^2|{R^{\prime }}_{N^{*}{i}_j}=k\right] \\ =\frac{1}{N^{*}}\sum _{k=1}^{N^{*}}\frac{k\left(N^{*}-k+1\right)}{{\left(N^{*}+1\right)}^2\left(N^{*}+2\right)}<\frac{1}{N^{*}}, \end{gathered}$$

which tends to 0 as N → ∞, where the expectation is interpreted as conditional on the labels. Therefore,

$$U_j=\underset{k\to \infty }{\lim }\frac{{R^{\prime }}_{N_k^{*}{i}_j}}{N_k^{*}+1}$$ (A.2)

for j ⩾ 1, with probability 1 for some subsequence $\left\{N_k^{*}\right\}$ of $\left\{N^{*}\right\}$, and hence U_j = h_j(R_N, N ⩾ 1, L₁, L₂, …) for some function h_j : Ω₁ × Ω₂ × … × {0, 1, 2}^∞ → [0, 1].

Now given $\left\{Q_{i_j}:L_{i_j}=0\right\}\stackrel{\text{i.i.d.}}{\sim }{\Phi }_{\left(g\right)}^{*}$, so that $\left\{U_j:L_{i_j}=0\right\}\stackrel{\text{i.i.d.}}{\sim }{V}_{\left(\mu ,\sigma ,g\right)}$, say, where V_(μ,σ,g) is the distribution of $\left\{\left(1-{\lambda }_{\left(\mu ,\sigma ,g\right)}^{*}\right){\Phi }_{\left(g\right)}^{*}+{\lambda }_{\left(\mu ,\sigma ,g\right)}^{*}{\Phi }_{\left(\mu ,\sigma ,g\right)}^{*}\right\}\left(\xi \right),\xi \sim {\Phi }_{\left(g\right)}^{*}$. Since clearly V_(μ,σ,g) is consistently estimable by the empirical distribution of (U_j : L_ij = 0), it now suffices to show that the family {V_(μ,σ,g) : μ, σ > 0} is identifiable.

If (μ₁, σ₁) and (μ₂, σ₂) are such that V_(μ1,σ1,g) = V_(μ2,σ2,g) then it follows that ${\lambda }_{\left({\mu }_1,{\sigma }_1,g\right)}^{*}={\lambda }_{\left({\mu }_2,{\sigma }_2,g\right)}^{*}$ and ${\varphi }_{\left({\mu }_1,{\sigma }_1\right)}^{*}={\varphi }_{\left({\mu }_2,{\sigma }_2\right)}^{*}$, which then implies that (μ₁, σ₁) = (μ₂, σ₂).

Therefore, there exists a function h of (U₁, U₂, …, L₁, L₂, …) and hence h* of all ranks and observed labels such that a.s. $\left[P_{{\mu }_0,{\sigma }_0,g,H}^{\infty }\right]$, we have

$$\begin{gathered} \left(\mu ,\sigma ,g\right)=h\left(U_1,U_2,\dots ,\right) \\ =h\left(h_1\left({\mathit{R}}_N,N⩾1,L_1,L_2,\dots \right),h_2\left({\mathit{R}}_N,N⩾1,L_1,L_2,\dots \right),\dots \right) \\ =h^{*}\left({\mathit{R}}_N,N⩾1,L_1,L_2,\dots \right). \end{gathered}$$