Figure 5.

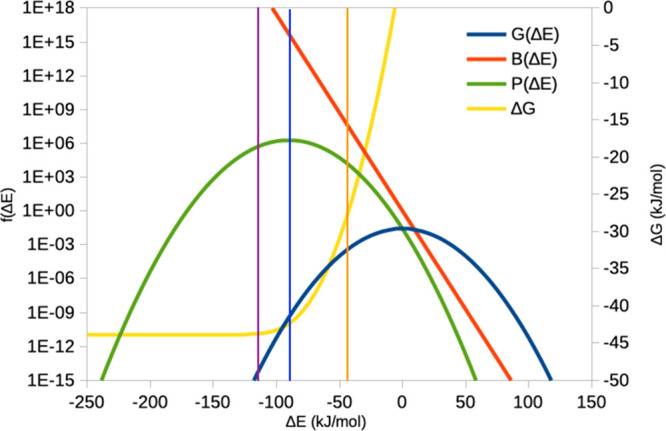
Problem of converging the exponential average. Assuming that ΔE follows a Gaussian distribution, the exponential average can be rewritten as an integral over the product of two terms 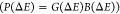, the Gaussian distribution 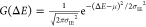and the Boltzmann factor 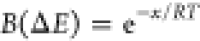.³⁰ These two terms are shown in the figure for the example of σ_IE = 15 kJ/mol (note the logarithmic scale). In this case, the maximum for the product is attained at ΔE = 90 kJ/mol (blue vertical line). At this value, G = 4 × 10^–10 (but B = 5 × 10¹⁵), so around 10¹⁰ snapshots are needed before this value is observed. In fact, ΔG and therefore ΔS (which is ΔG minus the average of ΔE) are still not fully converged (ΔG in the figure; right axis; it should be read from the right to the left, i.e., showing ΔG when all values larger than ΔE are included), differing by 1.4 kJ/mol from the analytic result; convergence to within 0.1 kJ/mol is obtained at ΔE = −115 kJ/mol, when G = 5 × 10^–15 (violet vertical line). If all ΔE < 3σ_IE (= −45 kJ/mol) are ignored, ΔG and TΔS will be wrong by over 15 kJ/mol (orange vertical line) because the most important parts of P are excluded.