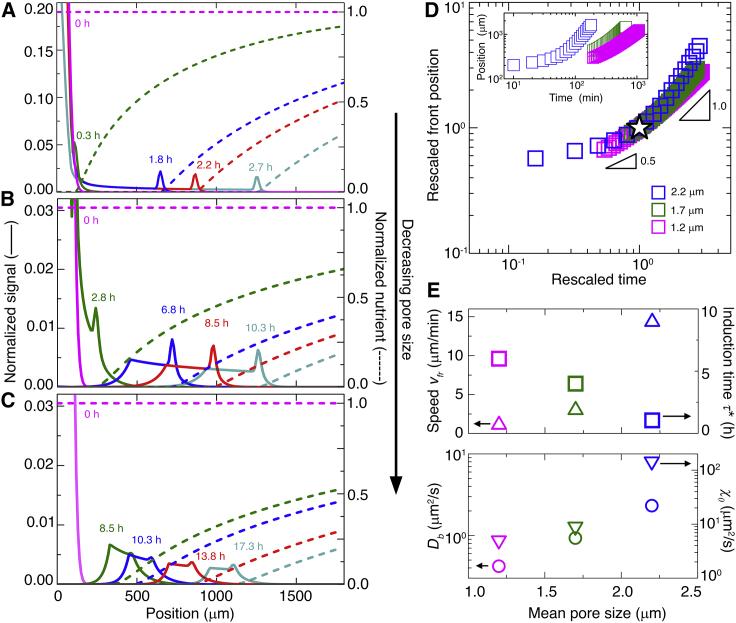
Figure 4.

Continuum model captures dynamics of propagating cellular fronts in porous media. (A–C) Numerical simulations of cellular signal (solid lines) and nutrient concentration (dashed lines), normalized by maximal initial value, for different radial positions and at different times. Top to bottom panels show results for media with a = 2.2, 1.7, and 1.2 μm, respectively. In all cases, the population initially spreads outward and then organizes into a front, indicated by the peak in the profiles, that propagates outward, as in the experiments. (D) Leading-edge position r of the propagating front over time t; inset shows raw data, and main panel shows data rescaled by the lengths and times (star) of the crossover from the short-time slow r ~t^1/2 scaling to the long-time fast r ~t¹ scaling. We observe slight deviations from the r ~t scaling for the a = 2.2 μm data at long times; these reflect the influence of boundaries in the system, as indicated by additional simulations (Fig. S10). (E) Upper panel shows variation of front propagation speed (upward triangles), determined from the long-time variation of the leading-edge position, and induction time (squares), defined as the time at which the crossover from the short-time slow r ~t^1/2 scaling to the long-time fast r ~t¹ scaling is observed, with mean pore size, as determined from the simulations. Lower panel shows variation of cellular diffusivity (circles), which is directly obtained from experiments, and chemotactic coefficient (downward triangles), which is determined from the simulations, with mean pore size. The uncertainty in front position in the top panel is determined by varying the threshold value used to determine the front position by ±10%. The uncertainty in the front speed v_fr is determined by computing the SD in the v_fr obtained by measuring the slope of the measured position versus time data for three successive 30 min periods at the end of the simulation, and the uncertainty in τ^∗ is again given by the temporal resolution of the simulation. In all cases, the error bars associated with the uncertainty in the measurements are smaller than the symbol size. To see this figure in color, go online.