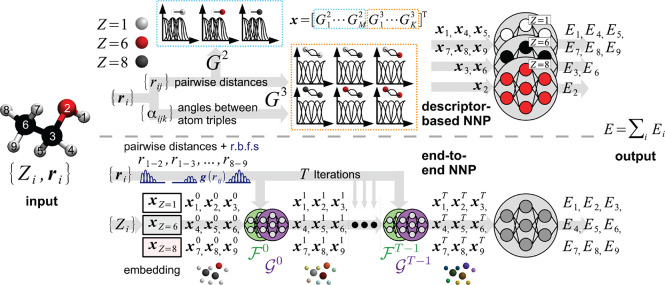
Figure 12.

Overview of descriptor-based (top) and end-to-end (bottom) NNPs. Both types of architecture take as input a set of N nuclear charges Z_i and Cartesian coordinates r_i and output atomic energy contributions E_i, which are summed to the total energy prediction E (here N = 9, an ethanol molecule is used as example). In the descriptor-based variant, pairwise distances r_ij and angles α_ijk between triplets of atoms are calculated from the Cartesian coordinates and used to compute hand-crafted two-body (G²) and three-body (G³) atom-centered symmetry functions (ACSFs) (see eqs 22 and 23). For each atom i, the values of M different G² and K different G³ ACSFs are collected in a vector x_i, which serves as a fingerprint of the atomic environment and is used as input to an NN predicting E_i. Information about the nuclear charges is encoded by having separate NNs and sets of ACSFs for all (combinations of) elements. In end-to-end NNPs, Z_i is used to initialize the vector representation x_i⁰ of each atom to an element-dependent (learnable) embedding (atoms with the same Z_i start from the same representation). 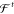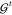Geometric information is encoded by iteratively passing these descriptors (along with pairwise distances r_ij expanded in radial basis functions g(r_ij)) in T steps through NNs representing interaction functions and atom-wise refinements (see eq 25). The final descriptors x_i are used as input for an additional NN predicting the atomic energy contributions (typically, a single NN is shared among all elements).