Figure 7.

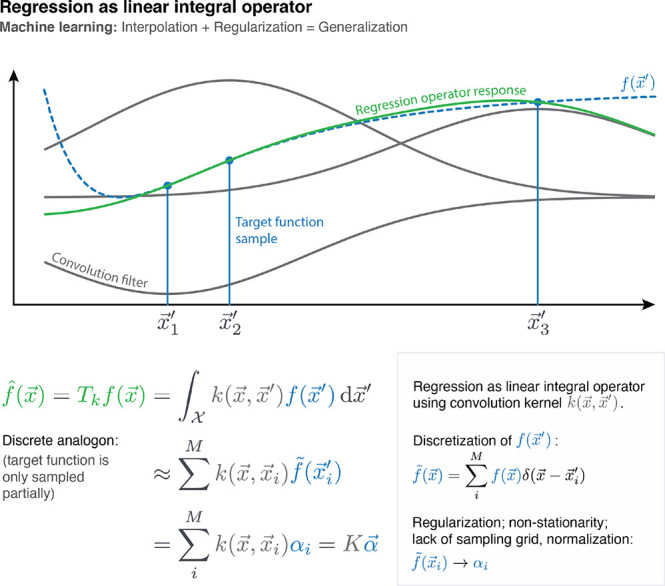
Kernel ridge regression can be understood as a linear integral operator T_k that is applied to the (only partially known) target function of interest f(x). Such operators are defined as convolutions with a continuous kernel function K, whose response is the regression result. Because the training data is typically not sampled on a grid, this convolution task transforms to a linear system that yields the regression coefficients α. Because only T_kf(x) and not the true f(x) is recovered, the challenge is to find a kernel that defines an operator that leaves the relevant parts of its original function invariant. This is why the Gaussian kernel (eq 4) is a popular choice: Depending on the chosen length scale γ, it attenuates high frequency components, while passing through the low frequency components of the input, therefore making only minimal assumptions about the target function. However, stronger assumptions (e.g., by combining kernels with physically motivated descriptors) increase the sample efficiency of the regressor.