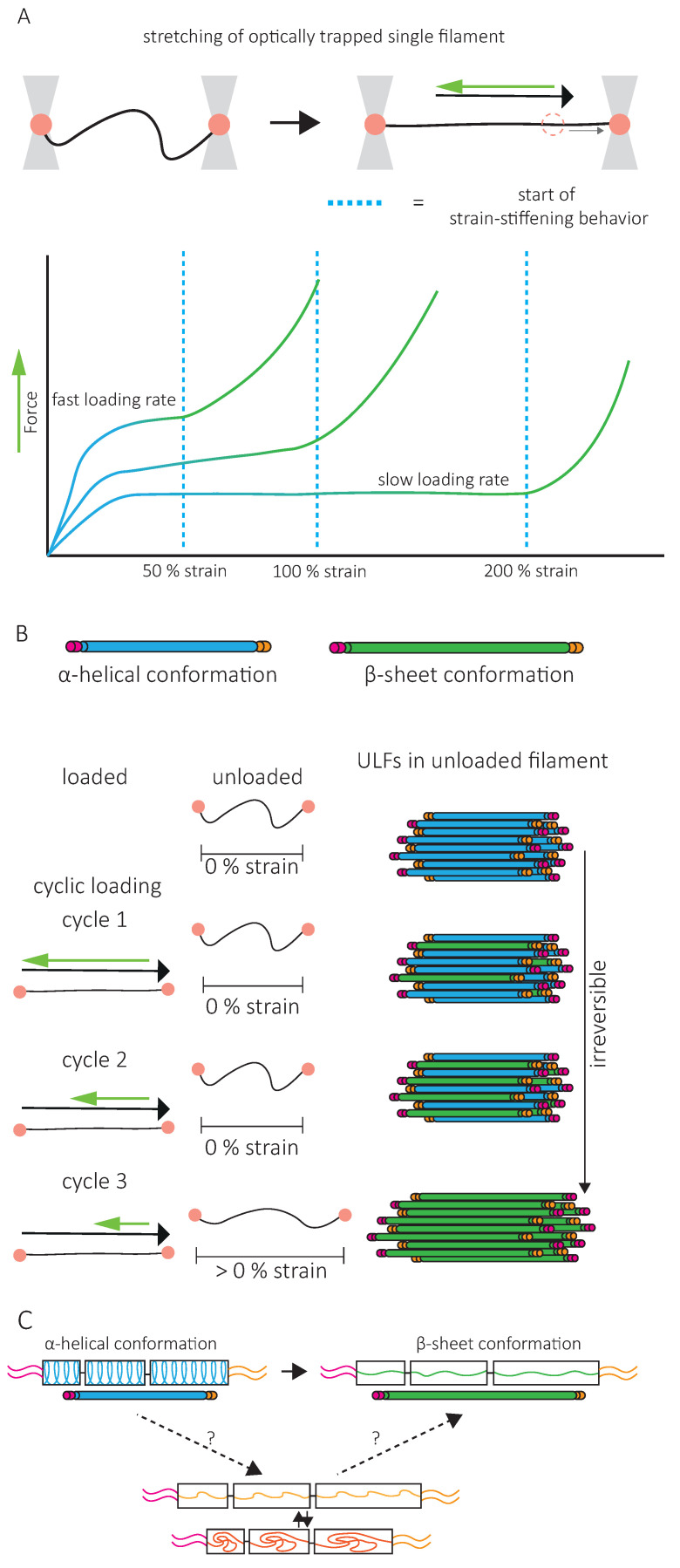
Figure 5.

Single intermediate filament mechanics and underlying conformational changes. (A). Optical trap of a single intermediate filament and force–strain curves generated from stretching a single filament at different loading rates. The curve is characterized by a steep increase in force at low strains derived from the stretching of the alpha-helices (blue line and dimer). This is followed by a plateau in the curve at intermediate strains, attributed to the unfolding of α-helices to β-sheet conformations (green line and dimer). At higher strains, the filament strain-stiffens as a result of pulling on β-sheets. Both filaments stretched by atomic force microscopy and optical trapping demonstrate this mechanical response. For fast loading rates, strain-stiffening is already observed at 50% strain, while at slow loading rates, strain-stiffening is not observed before 200% strain. (B). For repeated loading and unloading cycles, the force needed to reach the same strain decreases with each cycle. This is attributed to part of the dimers being in a β-sheet conformation (green) while others remain in an α-helical conformation (blue). Lower forces are required to unfold the remaining α-helices. The filament length after the loading force is released is determined by the shortest elements, thus α-helices. After all α-helices have switched to a β-sheet conformation, elongation of the unloaded filament can be observed. Experiments have shown that the original mechanical properties are irreversible within physiologically relevant recovery times. The β-sheet conformation requires energy and is in thermal unequilibrium. Upon unloading, the filament is expected to return to its α-helical thermal equilibrium conformation. However, the irreversibility of its original mechanical properties does not fit this explanation. (C). To explain the irreversibility of the original mechanical properties of single filaments, a third disordered conformational state has been proposed (orange), which can elongate (yellow) but cannot return back to an α-helical conformation. Adapted from Block et al., Phys. Rev. Lett 2017 & Forsting et al., Nano Letters 2019.