Figure 1.

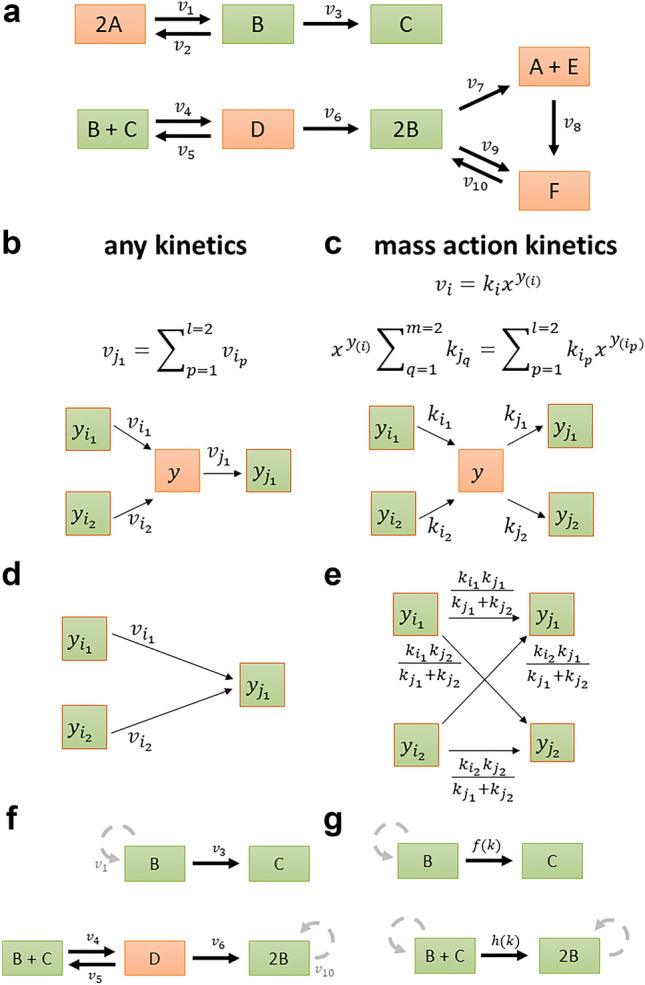
Balanced complexes for network reduction. (a) Toy example network borrowed from Shinar and Feinberg³³, including six species, A–F, eight complexes, depicted as rectangles, and ten reactions, with rates $v_1$–$v_{10}$, each connecting two complexes. Balanced complexes are shown in orange, while non-balanced complexes are depicted in green. Balanced complexes 2A, A + E, and F have one outgoing reaction, while the balanced complex D has more than one outgoing reaction. Structural motif allowing removal of the balanced complex $y$ (b) with single outgoing reaction, for an arbitrary kinetics and (c) with multiple outgoing reactions, for mass action kinetics. Removal of the complex amounts to substitution of variables, either with respect to reaction rates $v$ or monomials of species concentrations $x^y$, which can be represented by (d) network rewriting, for arbitrary kinetics and (e) additional scaling of reaction rate constants, with mass action kinetics. (f) Reduced network obtained by removing the balanced complexes 2A, A + E, and F; the loop reactions are shown in grey since they do not contribute to the stoichiometric matrix. (g) Reduced network obtained from the network in panel (f) after removal of the balanced complex D, assuming mass action. For simplicity, the rate constants are given as functions $f(k)$ and $h(k)$.