Emergence of Nonlinear Mixed Selectivity in Prefrontal Cortex after Training

Abstract

Neurons in the PFC are typically activated by different cognitive tasks, and also by different stimuli and abstract variables within these tasks. A single neuron's selectivity for a given stimulus dimension often changes depending on its context, a phenomenon known as nonlinear mixed selectivity (NMS). It has previously been hypothesized that NMS emerges as a result of training to perform tasks in different contexts. We tested this hypothesis directly by examining the neuronal responses of different PFC areas before and after male monkeys were trained to perform different working memory tasks involving visual stimulus locations and/or shapes. We found that training induces a modest increase in the proportion of PFC neurons with NMS exclusively for spatial working memory, but not for shape working memory tasks, with area 9/46 undergoing the most significant increase in NMS cell proportion. We also found that increased working memory task complexity, in the form of simultaneously storing location and shape combinations, does not increase the degree of NMS for stimulus shape with other task variables. Lastly, in contrast to the previous studies, we did not find evidence that NMS is predictive of task performance. Our results thus provide critical insights on the representation of stimuli and task information in neuronal populations, in working memory.

SIGNIFICANCE STATEMENT How multiple types of information are represented in working memory remains a complex computational problem. It has been hypothesized that nonlinear mixed selectivity allows neurons to efficiently encode multiple stimuli in different contexts, after subjects have been trained in complex tasks. Our analysis of prefrontal recordings obtained before and after training monkeys to perform working memory tasks only partially agreed with this prediction, in that nonlinear mixed selectivity emerged for spatial but not shape information, and mostly in mid-dorsal PFC. Nonlinear mixed selectivity also displayed little modulation across either task complexity or correct performance. These results point to other mechanisms, in addition to nonlinear mixed selectivity, representing complex information about stimulus and task context in neuronal activity.

Introduction

Working memory (WM) is broadly defined as the ability to encode, maintain, and manipulate information in the conscious mind over a period of seconds without the presence of any sensory inputs. As a core component of complex cognitive abilities, such as planning and reasoning, the true importance of WM ultimately depends on whether it can maintain and manipulate information in a task-relevant manner (Baddeley, 2012). Multiple variables, including external sensory inputs and internal task requirements, must be encoded to achieve the level of adaptability in WM that is necessary for complex tasks. The mechanisms that underlie this encoding process across time and neuronal population is one of the most important questions in current WM research.

When individuals are required to maintain objects in their WM, neurons from a network of brain regions may exhibit selective and sustained increases or decreases in their activity to represent the remembered objects through these unique patterns of activity (Constantinidis and Procyk, 2004). The PFC plays a leading role in this network, and by extension, in the use of WM (Riley and Constantinidis, 2016). For example, when the PFC is damaged or degraded, whether through trauma, illness, or experimental lesions, performance in WM tasks seems to decrease dramatically (Morris and Baddeley, 1988; Curtis and D'Esposito, 2004; Rossi et al., 2007).

Individual PFC neurons typically encode more than one variable in their activity, and the exact variables encoded are task-dependent (Asaad et al., 2000; Mansouri et al., 2006; Machens et al., 2010; Warden and Miller, 2010; Qi et al., 2015). More interestingly, a portion of neurons exhibit nonlinear mixed selectivity (NMS) for different variables, which means that their response to the combination of variables cannot be predicted by the linear summation of their responses to single variables (Rigotti et al., 2013; Parthasarathy et al., 2017; Johnston et al., 2020). Theoretical studies have shown that NMS is useful for linear readouts of flexible, arbitrary combinations of variables (Buonomano and Maass, 2009; Rigotti et al., 2010; Fusi et al., 2016), and may also control the trade-off between discrimination and generalization (Barak et al., 2013; Johnston et al., 2020).

Despite the proposed importance of NMS on theoretical grounds, some experimental studies have failed to detect neurons with NMS (Cavanagh et al., 2018). It is therefore possible that NMS may manifest exclusively in a limited set of PFC subdivisions or, alternatively, that NMS emerges exclusively after training to perform specific types of cognitive tasks. Moreover, the implications of NMS on other aspects of neural encoding, such as code stability, have not yet been investigated. We were therefore motivated to analyze and compare neural data from rhesus macaque monkeys before and after training. Here we report results of NMS as a function of task training, performance of different types of working memory tasks, and correct and error trials, across different prefrontal areas.

Materials and Methods

Animals

Data obtained from 6 male rhesus monkeys (Macaca mulatta, ages 5-9 years, weighing 5-12 kg), as previously documented (Riley et al., 2018), were analyzed in this study. None of these animals had any prior experimentation experience at the onset of our study. Monkeys were either single-housed or pair-housed in communal rooms with sensory interactions with other monkeys. All experimental procedures followed guidelines set by the US Public Health Service Policy on Humane Care and Use of Laboratory Animals and the National Research Council's Guide for the care and use of laboratory animals and were reviewed and approved by the Wake Forest University Institutional Animal Care and Use Committee.

Experimental setup

Monkeys sat with their heads fixed in a primate chair while viewing a monitor positioned 68 cm away from their eyes with dim ambient illumination and were required to fixate on a 0.2° white square appearing in the center of the screen. During each trial and to receive a liquid reward (typically fruit juice), the animals maintained fixation on the square while visual stimuli were presented either at a peripheral location or over the fovea. Any break of fixation immediately terminated the trial, and no reward was given. Eye position was monitored throughout the trial using a noninvasive, infrared eye position scanning system (model RK-716; ISCAN). The system achieved a <0.3° resolution around the center of vision. Eye position was sampled at 240 Hz, digitized, and recorded. The visual stimulus display, monitoring of eye position, and synchronization of stimuli with neurophysiological data were performed with in-house software implemented on the MATLAB environment (The MathWorks), using the Psychophysics Toolbox (Meyer and Constantinidis, 2005).

Pretraining task

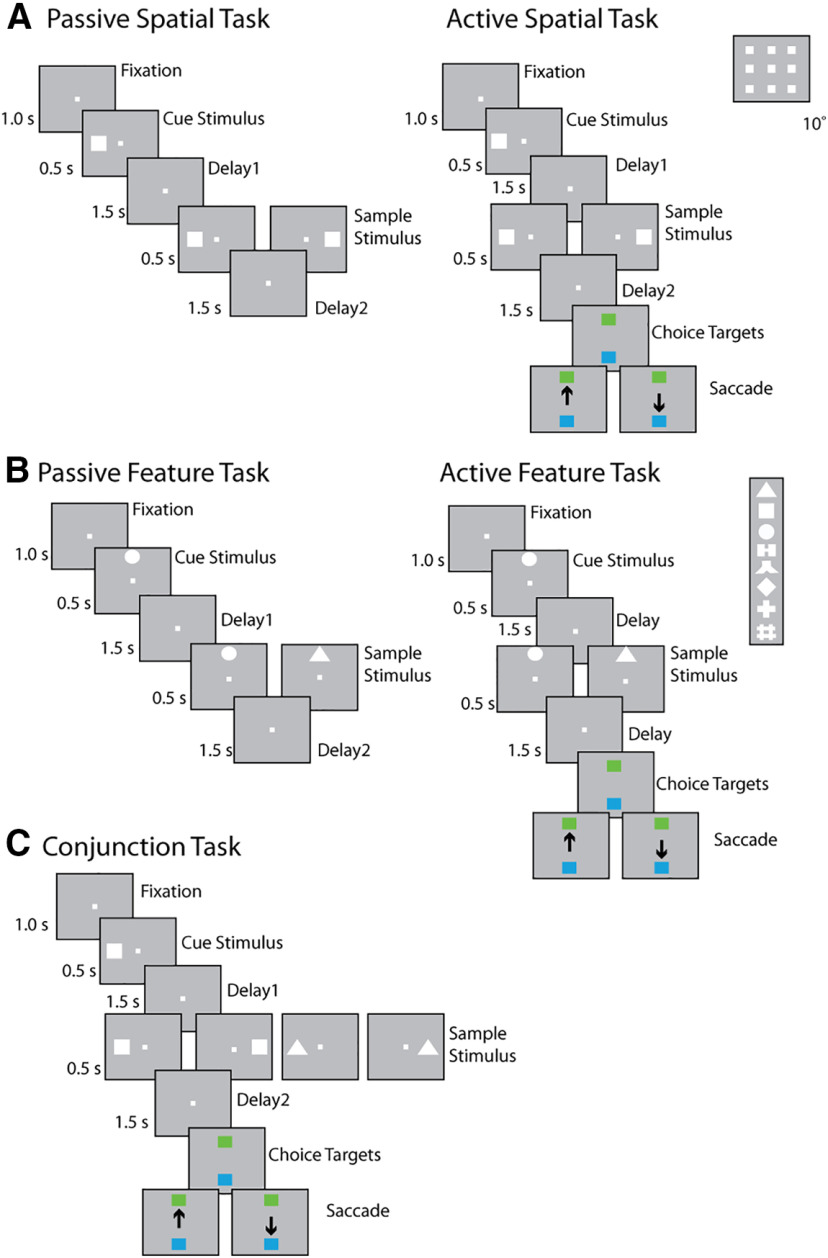
Following a brief period of fixation training and acclimation to the stimuli, monkeys were required to fixate on a center position while stimuli were displayed on the screen. The stimuli shown in the pretraining passive spatial task were white 2° squares, presented in one of nine possible locations arranged in a 3 × 3 grid with 10° distance between adjacent stimuli. The stimuli shown in the pretraining passive feature task were white 2° geometric shapes drawn from a set comprising a circle, diamond, the letter H, the hashtag symbol, the plus sign, a square, a triangle, and an inverted Y-letter. These stimuli could also be presented in one of nine possible locations arranged in a 3 × 3 grid with 10° distance between adjacent stimuli.

Presentation began with a fixation interval of 1 s where only the fixation point was displayed, followed by 500 ms of stimulus presentation (referred to hereafter as cue), followed by a 1.5 s “delay” interval (referred to hereafter as delay1) where, again, only the fixation point was displayed. A second stimulus (referred to hereafter as sample) was subsequently shown for 500 ms. In the spatial task, this second stimulus would be either identical in location to the initial stimulus or diametrically opposite the first stimulus. In the feature task, this second stimulus would appear in the same location to the initial stimulus and would either be an identical shape or the corresponding nonmatch shape (each shape was paired with one nonmatch shape). Only one nonmatch stimulus was paired with each cue, so that the number of match and nonmatch trials were balanced in each set. In both the spatial and feature task, this second stimulus display was followed by another “delay” period (referred to hereafter as delay2) of 1.5 s where only the fixation point was displayed. The location and identity of stimuli were of no behavioral relevance to the monkeys during the “pretraining” phase, as fixation was the only necessary action for obtaining reward.

Post-training task

Four of the six monkeys were trained to complete the active spatial, feature, and conjunction WM task. These tasks involved presentation of identical stimuli as the spatial and feature tasks during the “pretraining” phase, but now monkeys were required to remember the spatial location and/or shape of the first presented stimulus, and report whether the second stimulus was identical to the first or not, via saccading to one of two target stimuli (green for matching stimuli, blue for nonmatching). Each target stimulus could appear at one of two locations orthogonal to the cue/sample stimuli, pseudo-randomized in each trial.

The conjunction task combined the active spatial and feature tasks, using the same shape stimuli and presented at the same possible locations, with the same timing. In a single recording session, only four shape-location combinations involving two shapes and two locations were used. The conjunction task was the most complex task in the current study, as the monkeys were required to simultaneously store two different types of information, location and shape, in their working memory.

Surgery and neurophysiology

A 20-mm-diameter craniotomy was performed over the PFC, and a recording cylinder was implanted over the site. The location of the cylinder was visualized through anatomic MRI and stereotaxic coordinates after surgery. For 2 of the 4 monkeys that were trained to complete active spatial, feature, and conjunction WM tasks, the recording cylinder was moved after an initial round of recordings in the post-training phase to sample an additional surface of the PFC.

Anatomical localization

Each monkey underwent an MRI scan before neurophysiological recordings. Electrode penetrations were mapped onto the cortical surface. We identified six lateral PFC regions: a posterior-dorsal region that included area 8A, a mid-dorsal region that included area 8B and area 9/46, an anterior-dorsal region that included area 9 and area 46, a posterior-ventral region that included area 45, an anterior-ventral region that included area 47/12, and a frontopolar region that included area 10. However, the frontopolar region was not sampled sufficiently to be included in the present analyses.

Neuronal recordings

Neural recordings were conducted in the aforementioned areas of the PFC both before and after training in each WM task. Subsets of the data presented here were previously used to determine the collective properties of neurons in the dorsal and ventral PFC, as well as the properties of neurons before and after training in the posterior-dorsal, mid-dorsal, anterior-dorsal, posterior-ventral, and anterior-ventral PFC subdivisions. Extracellular recordings were performed with multiple microelectrodes that were either glass- or epoxylite-coated tungsten, with a 250-μm-diameter and 1-4 mΩ impedance at 1 kHz (Alpha-Omega Engineering). A Microdrive system (EPS drive, Alpha- Omega Engineering) advanced arrays of up to 8 microelectrodes, spaced 0.2-1.5 mm apart, through the dura and into the PFC. The signal from each electrode was amplified and bandpass filtered between 500 Hz and 8 kHz while being recorded with a modular data acquisition system (APM system, FHC). Waveforms that exceeded a user-defined threshold were sampled at 25 μs resolution, digitized, and stored for offline analysis. Neurons were sampled in an unbiased fashion, collecting data from all units isolated from our electrodes, with no regard to the response properties of the isolated neurons. A semiautomated cluster analysis relied on the KlustaKwik algorithm, which applied principal component analysis of the waveforms to sort recorded spike waveforms into separate units. To ensure a stable firing rate in the analyzed recordings, we identified recordings in which a significant effect of trial sequence was evident at the baseline firing rate (ANOVA, p < 0.05), for example, because of a neuron disappearing or appearing during a run, as we were collecting data from multiple electrodes. Data from these sessions were truncated so that analysis was only performed on a range of trials with stable firing rate. Less than 10% of neurons were corrected in this way. Identical data collection procedures, recording equipment, and spike sorting algorithms were used before and after training to prevent any analytical confounds.

Data analysis: neural selection

Data analysis was implemented with the MATLAB computational environment (The MathWorks), with additional statistic tests implemented through Originlab and StatsDirect. Peristimulus time histograms for illustrations were calculated through the moving window average method with a Gaussian window that had 200 ms SD, with the shaded area representing 2× SE cross trials. For all tasks, only cells with at least 12 correct trials for each cue-sample location/shape pair were included in the analysis. To classify neurons of the spatial task into different categories of selectivity, we performed two-way ANOVAs determining the influence of task factors on the neuron's spatial tuning. We set up this analysis in two different ways. In the initial two-way ANOVA, we analyzed firing only for the sample (second) stimulus in the task. The two factors were the location of the sample stimulus and its match or nonmatch status, thus quantifying whether tuning for the sample location depends on whether it is match or nonmatch. In a subsequent two-way ANOVA, we analyzed firing rate of both the cue (first) and sample (second) stimulus presentations, from match trials only. The two factors were stimulus location and the task epoch (first or second stimulus presentation), thus quantifying whether tuning is dependent on the order of stimulus presentation. Neurons with classical selectivity (CS) exhibited a main effect of only one factor without significant interaction term. Neurons with linear mixed selectivity (LMS) exhibited main effects of both factors without a significant interaction term. Neurons with NMS exhibited a significant interaction-term. Finally, nonselective (NS) neurons exhibited no significant main effects nor interaction term. Similarly, the two factors for feature task ANOVA analysis were stimuli shape × matching status, and stimuli shape × task epoch for the trial. The p < 0.05 level was chosen as the threshold for statistical significance for all ANOVA analysis. The animals were unable to predict the matching status of the trials during the fixation, cue, and delay1 periods; and as a result, the proportion of cells with significance for matching factor and the interaction term would not be expected to exceed 5% during these first three periods. Time bins used to calculate spike rate for different task stages are displayed in Figure 1. Choice period was defined as the 1 s interval after the choice array appears onscreen.

Figure 1.

Task structure and stimuli used. The animals were required to maintain center fixation throughout both active and passive task trials. At the end of active tasks trials, however, monkeys were required to make a saccade to a green target if the stimuli matched or to a blue target if the stimuli did not match. A, Spatial location match-to-sample task. Inset, Nine possible cue locations in a session. B, Shape feature match-to-sample task. Inset, Eight possible shapes in a session. C, Spatial-shape conjunction task; up to two locations and two stimuli shapes were used for any single particular session. Stimuli in all tasks extended 2 degrees of visual angle.

Dimensionality reduction

Our method for measuring dimensionality can be explained as follows: Let M be a dataset of size N × T × C, where N represents number of neurons, T indicates the number of trials, and C indicates the number of different conditions. In the case of our task, C would refer to all possible combinations of stimulus identity (location or feature) and match or nonmatch status. Each entry in this matrix represents the firing rate in a specified time bin, namely, the stimulus presentation period, or the delay period that follows it. Population response can thus be plotted across conditions and trials in an n-dimensional space. The plotting space is very high dimensional (dimensionality equals the number of cells), but most variance can be accounted for by a smaller number of axes if neural data are linearly correlated across conditions. As a result, the neural dimensionality is measured by the number of neural response subspace axes that explain this consistent variance, within the original n-dimensional space. In a fictitious noiseless case, where the response to each condition is identical in each trial, the dimensionality of the matrix could be reduced to that of the trial-averaged version of size N × C. The dimensionality of the matrix is equal to the number of nonzero singular values, which can be obtained by singular value decomposition (SVD), defined as follows:

$$M=U\Sigma V^T$$

In our context, M is the real number neural response data matrix. U is an N × N matrix, the columns of which provide a basis set of eigenvectors capturing the correlation among neurons, the weighted linear combination of which accounts for the variance in the original data. Σ is an N × C diagonal matrix with non-negative values equal to the square root of the eigenvalues, assigning weights to the columns of U. The dimensionality of the matrix is equal to the number of nonzero singular values. Finally, V is a C × C matrix mapping neuronal responses to stimulus conditions. However, the real data contain random noise that pushes data points away from a low dimensional manifold; thus, dimensionality results are almost always overestimated. For this reason, we used the cross-validation method developed by Ahlheim and Love (2018) to obtain a more accurate estimate of dimensionality for the real-word data. The basic idea is that the SVD operation could also be written in a linear equation form as follows:

$$\text{M}=u_1{\sigma }_1{v}_1^T+u_2{\sigma }_2{v}_2^T+...+u_c{\sigma }_c{v}_c^T$$

in which σ₁ ≥ σ₂ ≥ … σ_c ≥ 0 are singular values, u and v are the corresponding vectors from U and V, respectively. One can create a low dimensional approximation of M by gradually adding more terms that explain more variance. In the dimensionality estimation process, data from a total of j trials from each condition were first partitioned into three sets: a training set containing j-2 trials, a validation set containing 1 trial, and a testing set containing 1 trial. SVD was then applied to the averaged training dataset and used to reconstruct the training data from the U, Σ, and V-transpose matrices using increasing numbers of dimensions from 1 to the dimensionality of the training data. For each reconstructed matrix of different dimensionality based on the SVD, the Pearson correlation coefficient was computed between this result and the validation trial. This process was repeated over all possible partitions of the data into training and validation/testing sets. The dimensionality k that produced the highest mean correlation between the SVD reconstructed training data and the validation trial determined the dimensionality of the neural representation. The correlation of this representation with the held-out test data provided the final reconstruction correlation, as an estimate of reconstruction precision. A similar method has also been recently used to estimate the dimensionality over time for neural data (Cueva et al., 2020). The dimensionality of the sample and delay2 period in the spatial and feature task was calculated on 50 resamples of a 200-cell pseudo-population in the corresponding datasets.

Comparisons between areas and tasks

Only PFC areas with >50 cells in both pretraining and post-training time points were included in the subdivision mixed selectivity comparison analysis. Thus, for the feature task, only data from the mid-dorsal, posterior-dorsal, and posterior-ventral PFC were analyzed. For the spatial task, data from the mid-dorsal, posterior-dorsal, posterior-ventral, anterior-dorsal and anterior-ventral PFC were analyzed.

Neural data from tasks that applied the exact same visual stimuli were used to compare mixed selectivity between feature/spatial and conjunction tasks. For example, to compare the feature and the conjunction tasks, we started by selecting a subset of conjunction trials, in which both visual stimuli appeared at the same location as the corresponding feature task trials. The corresponding feature dataset was then drawn from a subset of feature task trials that used the same shape pairs as the chosen conjunction task trials. Our prior methods of ANOVAs could thus be applied for comparison across these datasets.

For comparing mixed selectivity in correct and error trials from the spatial task, we first examined F scores from the ANOVA of two task variables: the stimulus location and matching status. In this analysis, we used neurons that had at least three match and nonmatch trials for both the correct and error dataset, in at least three stimulus locations. The number of minimum trials and stimuli locations were chosen to maximize the average trial number for each cell included into the analysis, while still retaining a sufficiently large sample (i.e., >150 cells). The same number of trials from each stimuli location were randomly chosen in the correct and error dataset. This randomized trial selection process was repeated 50 times to make the best use of the uneven number of available trials in two datasets. We also analyzed factors of stimuli location and task epoch. For this analysis, we used neural data from match trials only, and from neurons that had at least four correct and error trials, in at least four stimuli locations. To calculate dimensionality in the spatial task in correct versus erroneous conditions, we first identified 56 cells with at least 4 trials in the same four conditions in both the correct and error datasets. We then randomly selected 50 cells to construct a pseudo-population for measuring dimensionality using the previously described SVD based method. This process was repeated 50 times to obtain a CI.

For decoding analysis of stimuli identity, matching status, or saccade directions, spiking responses from 1 s before cue onset to 5 s after cue onset were first binned using a 400-ms-wide window and 100 ms steps to create a spike count vector with a length of 57 elements. A pseudo-population was then constructed using the spike count vectors from all the available neurons of all the available animals, thus resulting in a dataset with 96 trials, as if they were recorded simultaneously. The population response matrix was z score-normalized before being used to train the decoder. A support vector machine (SVM) decoding algorithm with a linear kernel was implemented using the MATLAB fitcecoc function to decode stimuli location, stimuli shape, the match/nonmatch status of trials, or the saccadic direction. A 10-fold cross-validation method was used to estimate the decoder performance, and 20 random samplings were implemented to calculate a 95% CI. For the spatial and feature task, the decoding baseline for sensory information or saccadic direction was 12.5%, since there were 8 different options, and 50% for the matching status, since there were only 2 different options.

In the pretraining versus post-training decoding analysis, linear (CS and LMS) and nonlinear (NMS) neurons are first defined by their pretraining and post-training responses in the sample or delay2 period. Each classified population was then applied to decode sensory information (location and shape) and matching status. A randomization test was used to determine the time points at which decoding performance was significantly different between different selectivity categories. In short, we constructed the null distribution by randomly reassigning the cell selectivity labels under comparison, and recomputing the maximum absolute difference across all time points of the data in each iteration. This procedure was repeated for 5000 times. A difference was deemed to be significant if the true response difference occurred at the extremes of this null distribution (p < 0.05, two-tailed). Since every point in the null distribution is the maximum of all time points, this method already corrected for the multiple comparisons.

For saccadic decoding in the spatial task, we first constructed pseudo-populations by identifying neurons with correct and error trials in the same conditions (defined by saccadic direction and matching status). We then used correct trials to train a saccadic direction decoder. Only correct trials were used in the training dataset, as these would contain accurate representations of the saccadic direction information. Our decoder was subsequently used to predict saccade direction in a test dataset of both correct and error trials.

A Random “coloring” process was used as previously described (Rigotti et al., 2010) for the purpose of calculating the number of implementable binary classifications. Specifically, trials with 16 experimental (8 stimuli identities × 2 matching status) conditions were equally and randomly assigned one of two labels as the correct answer for binary classification training, making a total of 12,870 combinations with an equal number of conditions on each side of targeted decision boundary. An SVM decoder was then trained for every binary classification. A threshold of 80% correct for cross-validated decoding performance was used to define an “implementable” binary classification.

To more directly compare our results with previous research, a decoder was constructed to decode the matching or nonmatching status of a trial after pure selectivity for matching information was removed from each cell as reported previously (Rigotti et al., 2010). An SVM with a polynomial kernel was used to decode experimental conditions defined by cue location × matching status (16 conditions in total). We used the MATLAB fitcecoc function for this classification as well. In this case, the method produced a 16-bit binary output based on the firing rates of the neurons, which was compared with the expected binary output of each experimental condition; data from each trial were then classified into the category that was most similar (needed the smallest error correction). Four conditions were compared using this nonlinear decoder: 200 randomly selected informative cells (CS, LMS, and NMS defined in sample period) in the post-training condition, with unaltered selectivity profiles; 200 randomly selected informative cells in the post-training condition, with classical selectivity for matching status removed; 200 randomly selected informative cells in the pretraining condition, with classical selectivity for matching status removed; and 200 randomly selected classical selective cells in the post-training condition, with classical selectivity for matching status removed. The inclusion of the last condition is necessary to confirm the effectiveness of the pure selectivity removal process. We removed the classical selectivity for certain variables (e.g., matching status) of certain neurons by contaminating the firing rate recorded during one condition (sample match cue) with spikes recorded in the other condition (sample nonmatch to cue). More specifically, every time we sampled a spike count from a trial in condition c∈T₁, an additional noise source was artificially superimposed by adding a spike count sampled from a randomly selected trial in the same time bin, but belonging to a different condition c′∈T₂, in such a way that the classical selectivity for task variable T was equalized. The classical selectivity removal procedure can thus be formally denoted as the following equation:

$$v_i^c\left(t\right)=r_i^c\left(t\right)+{\displaystyle \sum }_{c}w{r}_i^{c^{\prime }}(t)$$

Where r_i^c(t) indicates spike count for neuron i at time t from a trial belonging to condition c, where c∈T₁, and v_i^c(t) refer to the response of the same neuron at the same time point, after removing the classical selectivity for task variable T, {T₁,T₂,…}∈T. Finally, wr_i^c′(t) represents a random variable that selects a condition c′∉T₁ at random.

Only informative neurons (CS, LMS, and NMS neurons) in the delay2 period were used for the cross temporal decoding analysis, since we wanted to explore the decoding dynamics during the delay period. The linear SVM decoder was trained on individual time points and thus had 57 linear decision boundaries. The same dataset was then classified by every decision boundary in the vector to produce a 57 × 57 matrix, a process that was repeated 20 times to eliminate the noise. The decoding performance matrix for each condition was normalized individually to highlight the coding dynamics rather than absolute performance. A permutation-based test was used to determine the difference in the stability of different cell population recordings. For every permutation cycle, we randomly shuffled the labels of selectivity category for all cells; then we trained separate decoders for different populations based on the new shuffled labels, and two sample t tests were run on all corresponding pairs between decoding performance matrix of linear and nonlinear populations. We ran 1000 such permutations to construct a null distribution of the chosen statistic value (p value). p values obtained from the original dataset that exceeded 5% threshold were considered statistically significant.

Data availability

All relevant data and code will be available from the corresponding author on reasonable request. MATLAB decoder code is available at https://github.com/dwhzlh87/mixed-selectivity.

Results

Extracellular neurophysiological recordings were collected from the lateral PFC of 6 monkeys before and after they were trained to perform the match/nonmatch WM tasks (Meyer et al., 2011; Riley et al., 2018). The task required them to view two stimuli appearing in sequence with an intervening delay period between them, and after a second delay period to report whether or not the second stimulus was identical to the first. The two stimuli could differ in terms of their location (spatial task, Fig. 1A), shape (feature task, Fig. 1B), or both (conjunction task, Fig. 1C). If the second stimulus matched with the first, monkeys would saccade toward a green target during a subsequent interval. Otherwise, they would saccade to a blue target at a diametrical location. Monkeys were able to perform all three tasks with accuracy much higher than chance level (mean performance: spatial task 86.2%, feature task 82.1%, conjunction task 81.0%).

A total of 1617 cells from 6 monkeys were recorded while the animals viewed the spatial stimuli passively, and 1493 cells from 5 monkeys were recorded while the animals viewed the feature stimuli passively, before any training. A total of 1104 cells from 3 monkeys and 1091 cells from 2 monkeys were collected while the animals were performing the active spatial and feature tasks, respectively, which were mutually called “post-training.” We also collected neural data from 247 neurons for the passive spatial task from 2 monkeys after they were trained in the active spatial task. An additional 975 cells from 2 monkeys were collected while they were performing the active, post-training conjunction task.

Types of selectivity in individual neuronal responses

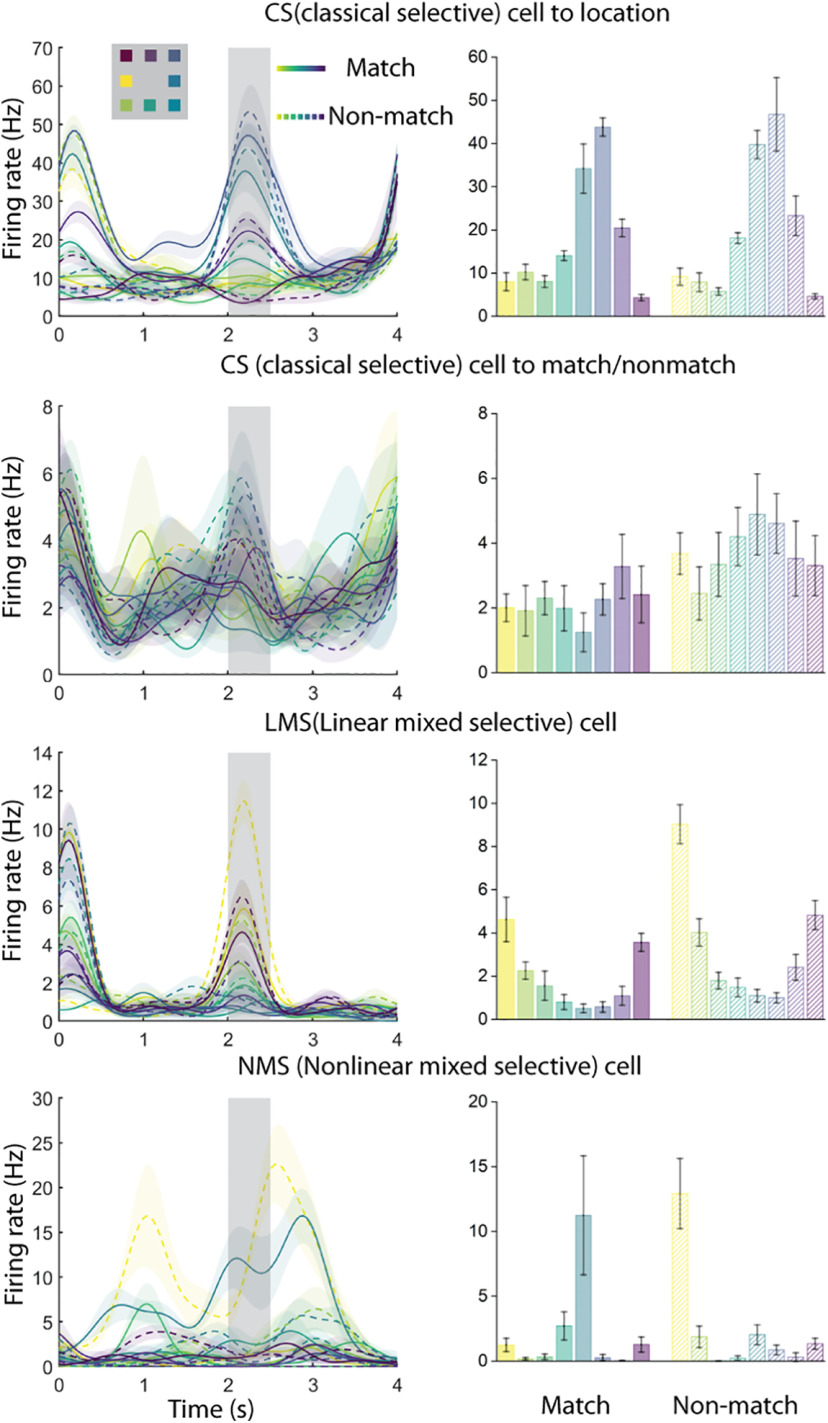
In our tasks, the context of a given stimulus depends on the task interval and sequence in which it is presented. We first considered how selectivity for stimulus location and shape in the spatial, feature, and conjunction WM tasks may vary when the same sample stimulus appears as a match (i.e., it is preceded by a cue at the same location/shape) or a nonmatch (i.e., is preceded by a cue stimulus of a different location/shape). The neuronal firing rate in a dataset is therefore a function of the stimulus location or shape, and whether the sample stimulus matched the cue stimulus. We used a two-way ANOVA with factors of stimulus location/shape and match/nonmatch status to classify neurons into four categories of selectivity. CS neurons exhibited a significant main effect to only one of the factors (stimulus identity or matching status) and had no significant interaction term. In Figure 2, the first exemplar set of plots depicts such a CS cell, selective exclusively for the location of the stimuli, which does not respond differently regardless of whether the stimulus appeared as a match or nonmatch. The second exemplar of Figure 2 displays another CS cell not selective for the location of the stimuli but demonstrating higher mean response when the stimulus appeared as a nonmatch. LMS neurons exhibited a significant main effect for both factors but had no significant interaction term. The third exemplar of Figure 2 displays such an LMS neuron demonstrating a higher mean response when stimuli appear as nonmatch, while simultaneously displaying the same rank order preference for location. NMS neurons exhibited a significant interaction effect, as shown in the last exemplar in Figure 2, a neuron demonstrating different selectivity pattern for locations under match versus nonmatch conditions. Finally, NS indicated the neurons with no selectivity to any factors or their interaction under consideration. These analyses were performed using the firing rate recorded during the stimulus presentation period, and again, using the firing rate recorded during the delay period that followed it.

Figure 2.

Exemplar neural responses from the spatial task for CS, LMS, and NMS cells, defined by the task variables of stimulus location and match status. Selectivity classification was based on the spike responses of the 500 ms sample period (indicated by the gray shaded area from 2 to 2.5 s). The locations of the stimuli were color-coded. Solid line represents the stimulus when it was a match. Dashed line represents the stimulus when it was a nonmatch. Shaded regions and error bars represent ±SE of firing rate.

A second type of NMS was identified in terms of selectivity for stimulus sequence, that is, whether the same stimulus appeared first (cue) or second (sample). To avoid the confound of the match or nonmatch status of the second stimulus, we relied exclusively on match stimuli. This form of NMS was also evaluated through a two-way ANOVA model, identifying CS, LMS, NMS, and NS neurons in terms of how the neurons represented the exact same stimulus when it appeared as a cue and as a match stimulus.

Effects of training on NMS

For both types of NMS we examined (stimulus selectivity x match/nonmatch or cue/match), the proportion of NMS neurons after training increased more for the spatial than the feature working memory task. When we used the factors of stimulus location/shape and match/nonmatch status for our two-way ANOVA, we found that training in the spatial WM task increased the proportion of NMS cells in both the sample period and the delay period that followed the sample (sample period: pretraining proportion = 6.2%, post-training proportion = 12.3%, two-sample proportion test, z = 5.31, p = 1.13 × 10⁻⁷; delay2 period: pretraining proportion = 2.8%, post-training proportion = 6.2%, two-sample proportion test, z = 4.62, p = 4.86 × 10⁻⁵). However, this increase in selectivity was not exclusive to NMS cells. The proportion of CS cells also increased in the delay period following the sample (pretraining proportion = 10.6%, post-training proportion = 14.8%, two-sample proportion test, z = 3.19, p = 0.0014).

The increase in NMS cells was not evident for all types of training. When we looked at the proportion of change across the pretraining and post-training feature task, we only found an increase of proportion for CS cells (sample period: pretraining proportion = 12.0%, post-training proportion = 15.7%, two-sample proportion test, z = 2.65, p = 0.0081; delay2 period: pretraining proportion = 9.0%, post-training proportion = 22.6%, two-sample proportion test, z = 9.37, p = 3.4 × 10⁻²⁰). No significant increase in the proportion of NMS cells was observed (sample period: pretraining proportion = 5.8%, post-training proportion = 6.7%, two-sample proportion test, z = 1.01, p = 0.314; delay2 period: pretraining proportion = 4.2%, post-training proportion = 4.6%, two-sample proportion test, z = 0.522, p = 0.602) (Fig. 3A,B).

Figure 3.

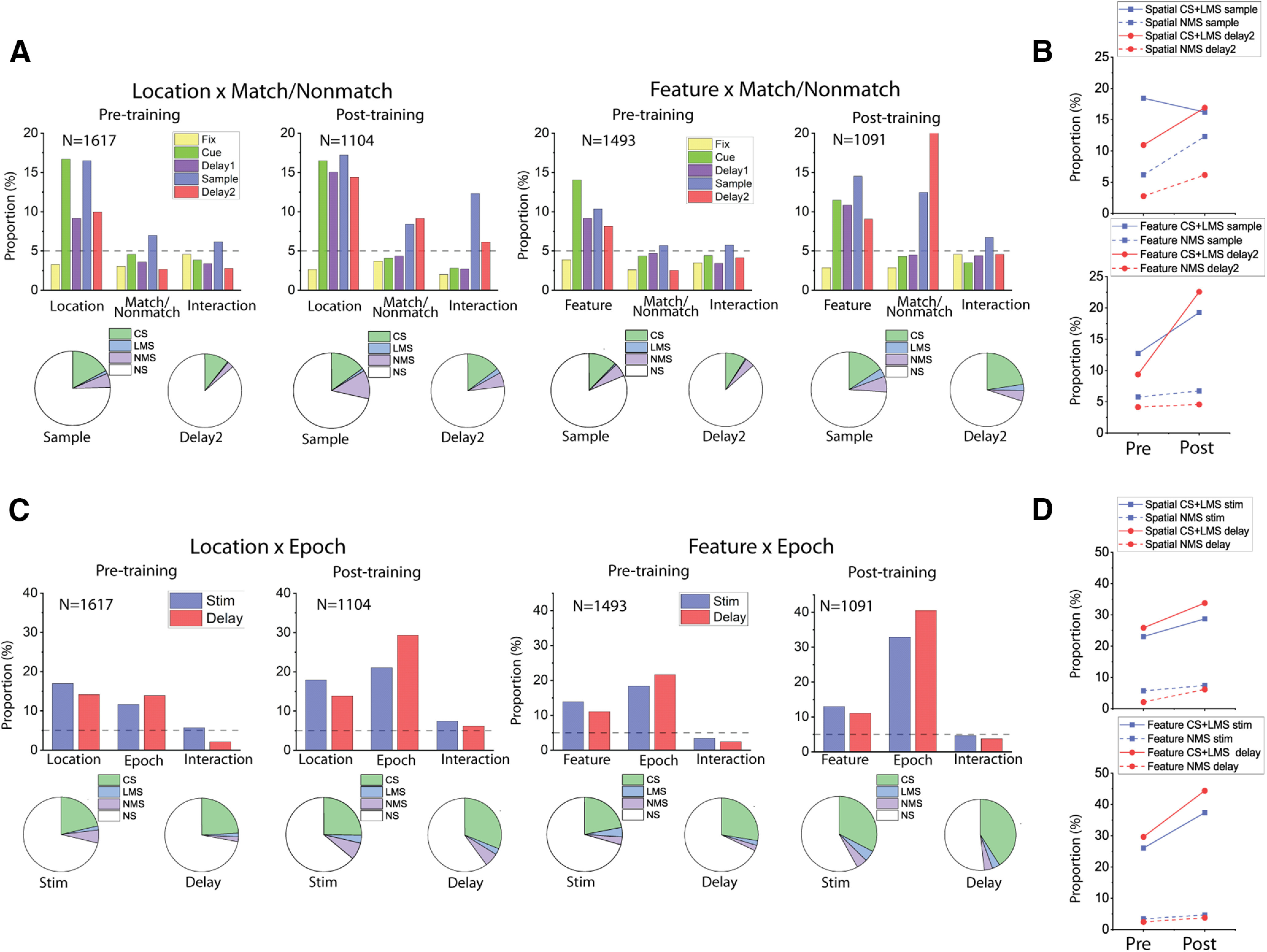
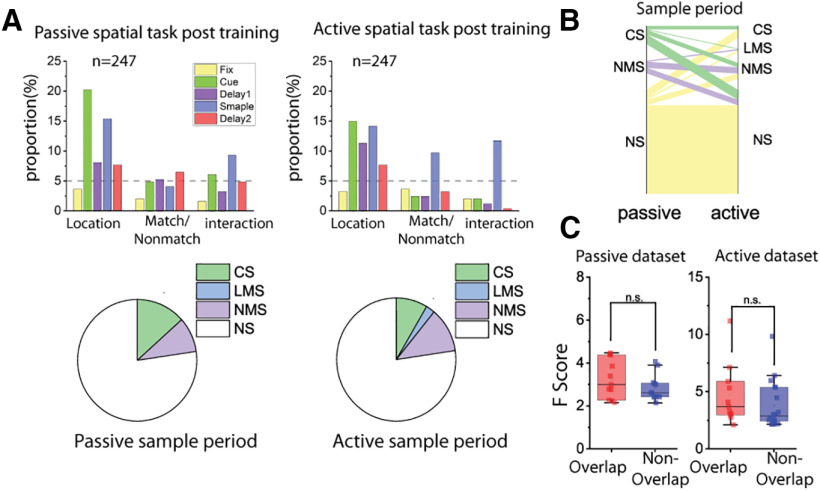
Training increased mixed selectivity preferentially in the spatial task. A, Bar graphs represent the proportions of cells tuned to stimuli identities (Location/Shape), matching status, and their interaction (i.e., NMS) in different stages of the task trials, both before and after the animals were trained for the active tasks. Pie charts represent the proportion of different selectivity categories (NS, CS, LMS, and NMS) in the sample and delay2 periods of both tasks, both before and after the animals were trained for the active tasks. Green areas in pie chart are the combined proportion of classically selective cells for both factors used in the two-way ANOVA. B, Plots of corresponding proportion changes. C, Same as in A, but examining the interaction between stimuli identities (Location/Shape), and task epoch (cue/delay1 vs sample/delay2 period), instead of trials matching status. D, Plots of corresponding proportion changes.

Similar results were observed when we used the factors of stimulus location/shape and task epoch (cue vs match) for the two-way ANOVA (Fig. 3C,D). For the spatial task, training increased the proportion of NMS cells, at least in the delay period (stimulus period: pretraining proportion = 5.7%, post-training proportion = 7.4%, two-sample proportion test, z = 1.78, p = 0.075; delay period: pretraining proportion = 2.1%, post-training proportion = 6.2%, two-sample proportion test, z = 5.03, p = 4.94 × 10⁻⁷). A similar increase was observed for the CS cells (stimulus period: pretraining proportion = 21.3%, post-training proportion = 25.3%, two-sample proportion test, z = 2.37, p = 0.018; delay period: pretraining proportion = 24.2%, post-training proportion = 31.1%, two-sample proportion test, z = 3.93, p = 8.53 × 10⁻⁵). In the feature task, only the proportion of CS cells changed (stimulus period: pretraining proportion = 21.9%, post-training proportion = 32.6%, two-sample proportion test, z = 6.05, p = 1.45 × 10⁻⁹; delay period: pretraining proportion = 27.6%, post-training proportion = 41%, two-sample proportion test, z = 7.16, p = 8.32 × 10⁻¹³). The proportion of NMS cells with an effect in the stimulus period remained relatively unchanged for the cue/match period (pretraining proportion = 3.4%, post-training proportion = 4.7%, two-sample proportion test, z = 1.59, p = 0.112), as well as the delay period (pretraining proportion = 2.4%, post-training proportion = 3.8%, two-sample proportion test, z = 1.95, p = 0.051). We did not have sufficient power to perform this analysis individually for all animals, but for 2 subjects with sufficient data in both the feature and spatial tasks, lack of substantial NMS in the feature task after training was evident in both. For the sample period in Subject A, the NMS proportion was 3.6% and 6.5% for the pretraining and post-training periods, respectively (two-sample proportion test, z = 0.93, p = 0.352). For Subject A, it was 6.4% and 6.9%, respectively (two-sample proportion test, z = 0.37, p = 0.709). In the delay2 period, the proportion of NMS neurons in Monkey A was 1.8% and 3.8% for the pretraining and post-training periods, respectively (two-sample proportion test, z = 0.93, p = 0.407). For Monkey E, it was 5.5% and 4.8%, respectively (two-sample proportion test, z = 0.42, p = 0.672).

To further validate our proportional measure for NMS and compare our results with previous research on NMS in the PFC, we plotted the F scores for the interaction term (i.e., stimulus identity × matching status) in both the spatial and the feature task (Fig. 4A). We found that this measure of NMS for individual cells increased specifically for the spatial task, indicated by slightly higher mean F score values after training. Importantly, this slight increase in mean is not trivial considering that the proportion of NMS is relatively low.

Figure 4.

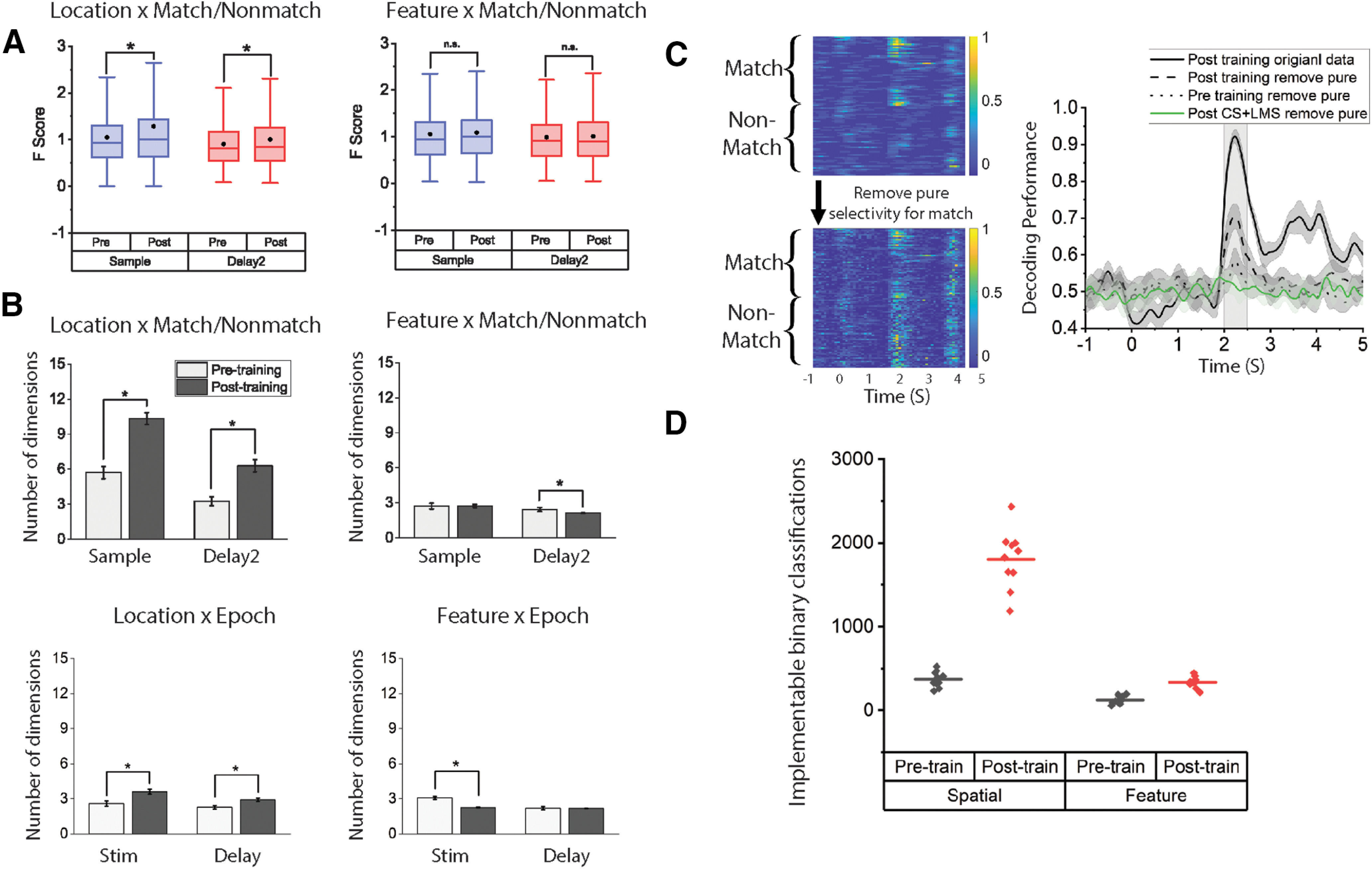
A, Analysis of the F scores from all recorded neurons for the interaction term (stimuli identity × match/nonmatch) shows that the degree of nonlinear mixed selectivity increased after training for the spatial task only. Black dots in the box represent mean. Box boundaries indicate 25%-75% range. Whiskers represent 1.5 IQR. B, Dimensionality measure of neural responses in the spatial (left) and feature (right) task, before and after training in the active tasks. To measure dimensionality, SVD was applied to a matrix containing data across all task conditions, based on the factors used for each analysis. In the case of Location × Match/Nonmatch NMS analysis, data included sample firing rates for all location × Match/Nonmatch combinations. For Location × Epoch NMS analysis, data included firing rates for different locations in either the cue or the sample period of match trials. C, Decoding with pure selectivity removed. Left, Example of an NMS cell in the sample period with pure selectivity to match/nonmatch status removed. Color in the heat maps coded for the normalized neuronal response ranging from 0 (blue) to 1 (yellow). y axis in the heat map organizes trials by matching status and then by stimuli location. Right, Decoding for matching status for the spatial task before and after removing pure selectivity of match/nonmatch status across pretraining and post-training; 200 cells in each dataset were randomly chosen to construct 10 pseudo-populations to calculate the CI. Nonlinear information increased after training. D, Number of implementable binary classifications for different tasks and in different training stages. Data from sample period for both tasks. * represents p < 0.05.

To quantify the change in NMS in an alternative way, we also measured the dimensionality of population responses in the sample and delay2 period for the spatial and feature task. Again, this analysis confirmed the results of our cell proportion measure (Fig. 4B). For the spatial task, there was a significant increase of dimensionality after training for both types of NMS. For NMS defined as the location × matching effect, that is, different selectivity for the same stimulus when it appeared as a match or a nonmatch, dimensionality increased after training in the sample period (pretraining dimensionality = 5.72, post-training dimensionality = 10.33, two-sample t test, t₍₉₈₎ = 12.21, p = 2.18 × 10⁻²¹) as well as in the delay2 period (pretraining = 3.25, post-training dimensionality = 6.29, two-sample t test, t₍₉₈₎ = 9.39, p = 2.51 × 10⁻¹⁵). For NMS defined as the location × epoch effect, that is, different selectivity for a stimulus when it appears first in the sequence versus second in the sequence dimensionality increased after training for the stimulus presentation period (pretraining dimensionality = 2.58, post-training dimensionality = 3.61, two-sample t test, t₍₉₈₎ = 6.42, p = 5.01 × 10⁻⁹) as well as in the delay period (pretraining dimensionality = 2.67, post-training dimensionality = 2.91, two-sample t test, t₍₉₈₎ = 5.76, p = 2.51 × 10⁻⁸). For the feature task, however, no significant increase was observed in the mean F score (Fig. 4A) or dimensionality (Fig. 4B). This was true for both the shape × matching comparisons (sample period: pretraining dimensionality = 2.72, post-training dimensionality = 2.73, two-sample t test, t₍₉₈₎ = 0.027, p = 0.978; delay2 period: pretraining dimensionality = 2.43, post-training dimensionality = 2.11, two-sample t test, t₍₉₈₎ = 3.49, p = 7.29 × 10⁻⁴) and the shape × epoch comparisons (stim period: pretraining dimensionality = 3.08, post-training dimensionality = 2.31, two-sample t test, t₍₉₈₎ = 10.27, p = 1.36 × 10⁻¹⁷; delay period: pretraining dimensionality = 2.18, post-training dimensionality = 2.11, two-sample t test, t₍₉₈₎ = 0.84, p = 0.40). In accordance with previous research (Rigotti et al., 2013), we found that the increased dimensionality in the spatial task was accompanied by an increased number of implementable binary classifications (Fig. 4D), as well as enhanced decoding after pure selectivity was removed (Fig. 4C).

Previous studies of NMS have suggested that increased linear classification boundary choices would be beneficial for downstream readout cells, which are mostly likely action-related. We thus investigated the saccade-related signals in recorded cells to determine whether action information exists preferentially in different selective categories (CS vs NMS), by defining different types of selectivity (CS, LMS, NMS) through the same method we used for the sample and delay2 period. Although there was strong selectivity for saccade locations, we ultimately found very little NMS for saccade direction and matching status (further discussed in the last section of the results).

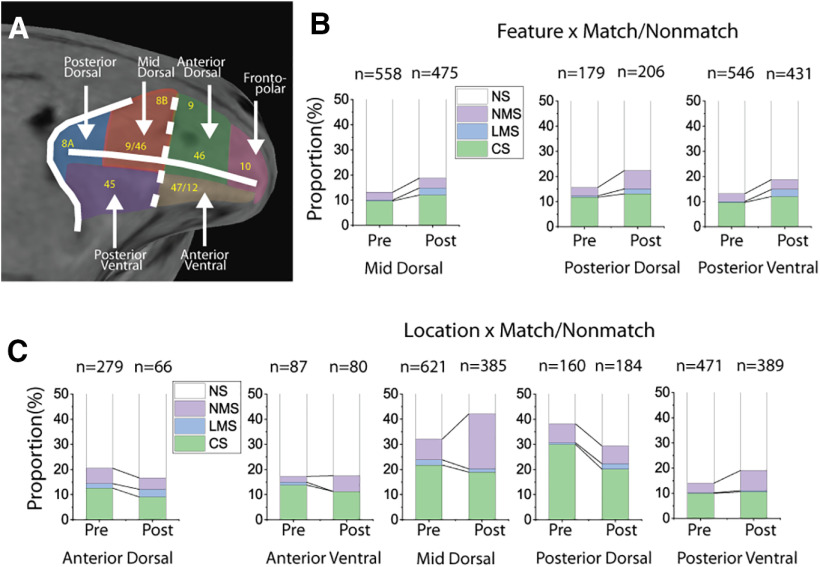
Regional localization of NMS

To assess whether specific subregions of the PFC may be specialized for NMS, we divided the lateral PFC into regions (Fig. 5A) and analyzed the respective neurophysiological data from five of these regions to determine the different areas' proportional contributions to the observed changes in NMS. We examined NMS defined by location/shape and match/nonmatch status in the sample period and ultimately found that the mid-dorsal subdivision underwent the greatest proportional change in NMS cells for the spatial task after training (Fig. 5C), without a comparable increase in the proportion of CS neurons (mid-dorsal: CS 21.7% pretraining to 19.0% post-training, NMS 8.2% pretraining to 21.8% post-training). For the feature task, however, the proportional change in NMS cells was relatively small, with moderate increases in CS and LMS observed in all three analyzed areas (Fig. 5B).

Figure 5.

Cell selectivity changes by brain regions. A, PFC subdivisions that were used for recording in the current study. B, The effects of training in the active feature task on the proportion of different selectivity categories (NS, CS, LMS, and NMS) in the sample period. There were significant increases in the proportion of LMS cells in all three PFC regions included for analysis, but relatively low increases in the proportion of NMS cells. C, The effects of training in the active spatial task on the proportion of different selectivity categories (NS, CS, LMS, and NMS) in the sample period. The greatest increase in NMS occurred at the mid-dorsal region.

NMS in task context

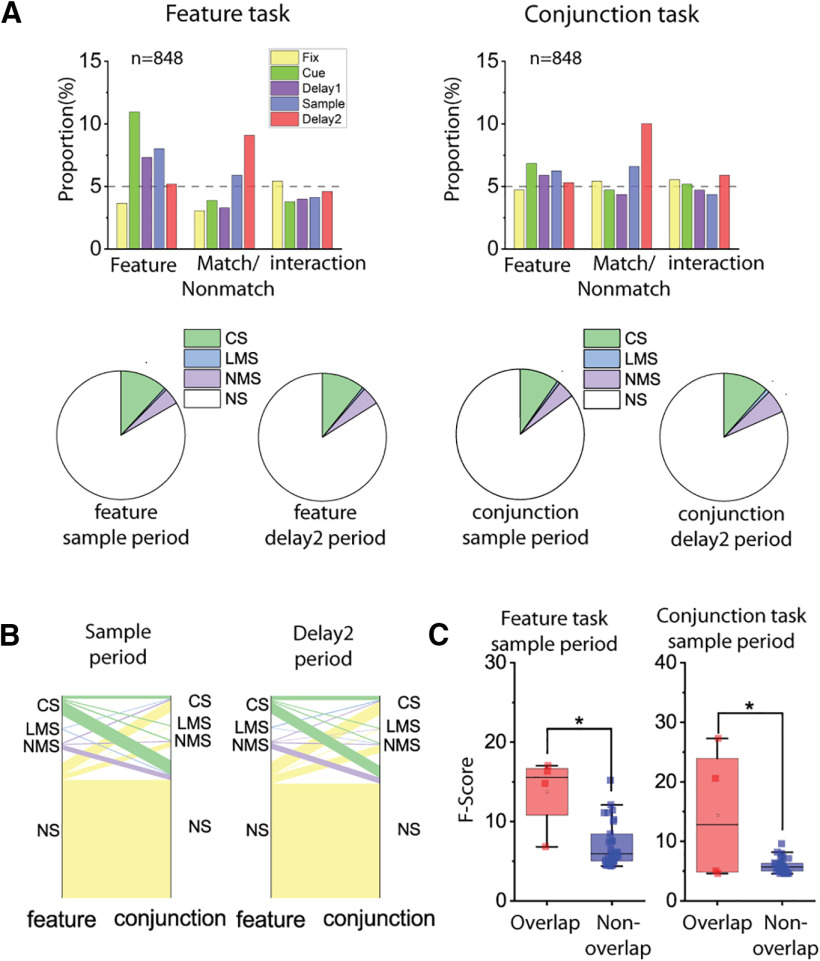
Previous theoretical studies linked NMS with more flexible readouts of multiple task variables, thus leading to the hypothesis that task complexity may modulate NMS. To test this hypothesis, we compared the neural responses to different shapes at the same location when the stimuli appeared as match or nonmatch in the conjunction task, to the same neurons' responses to the same stimuli when they appeared in the feature task. In the conjunction task, animals needed to simultaneously remember both location and shape of visual stimuli, while in the feature task, they were only required to remember shape. Although the hypothesis predicted that the conjunction task would result in greater NMS than the feature task when the sensory stimuli were the same, this was not what we observed. No significant differences were observed for either flin CS cells or NMS cells in either the sample period or the delay2 period that followed. For CS cells in the sample period, the feature task proportion was 11.9%, whereas the conjunction task proportion was 9.9% (exact matched pair sample proportion test, F = 1.229, p = 0.197); in the delay2 period, the respective proportions for the feature task was 10.8%, and for the conjunction task, 11.6% (exact matched pair delay2 proportion test, F = 1.069, p = 0.681). For NMS cells in the sample period, the feature task proportion was 4.1%, and the conjunction task proportion was 4.4% (exact matched pair sample proportion test, F = 1.031, p = 0.901). In the delay2 period, the feature task proportion = 4.6%, conjunction task proportion = 5.9% (exact matched pair delay2 proportion test, F = 1.278, p = 0.266) (Fig. 6A).

Figure 6.

Cell selectivity in tasks with different levels of complexity. Analyses were performed on neural data from the same population of cells, with matching numbers of trials in the feature and the conjunction tasks. Only trials with the same stimuli were included in this analysis. A, Examining interaction (NMS) across stimulus preference and matching status. Bar graphs represent the proportions of cells tuned to stimuli shape, trials matching status, and their interaction in different stages of both the feature and conjunction tasks. Pie charts represent the proportion of different selectivity categories (NS, CS, LMS, and NMS) in corresponding sample and delay2 periods. B, Flow diagram represents cell selectivity category mapping across tasks. On the left side of each plot, cell selectivity category (NS, CS, LMS, and NMS) in the feature task was color-coded. The thickness of lines represents the number of cells. The right side of each plot represents selectivity categories of the same cells in the conjunction task. The composition of cell selectivity category with reference to the other task is shown by the proportion of different colored lines. C, F scores of the interaction term in the ANOVA were compared between cells that were classified as NMS cells in both tasks (overlapping cells), and those only classified as NMS in one of the tasks (nonoverlapping cells). * represents p < 0.05.

We also examined changes in individual cells' selectivity across the feature and conjunction tasks. A change in selectivity type was frequent between tasks; most CS and NMS cells, defined as such as in the feature task, changed their selectivity type in the conjunction task (CS cells: 85.2% in sample period, 77.2% in delay2; NMS cells 88.6% in sample period, 89.7% in delay2). The finding implies that CS and NMS selectivity is task-specific, and an unstable mapping exists between different tasks (Fig. 6B). Although the percentage of NMS neurons was close to that expected by chance, NMS cells with a larger degree of interaction in one task tend to also fall into the NMS category in the other task (Fig. 6C). No significant difference was observed in the proportion of NMS cells when we performed a similar comparison between the spatial and conjunction task; the proportion of NMS cells in the spatial task was 18.3%, whereas in the conjunction task it was = 14.1% (two-sample proportion test, z = 0.68, p = 0.494). In the delay2 period, the same proportions were 7.0% and 11.3%, respectively (two-sample proportion test, z = 0.88, p = 0.381).

The comparison of the naive and trained conditions allowed us to test the overall incidence of NMS in different populations of PFC neurons, sampled randomly before and after training, which was conducted over the course of several months. If NMS were critical for the representation of task-relevant information, we would expect fewer neurons to exhibit NMS, when animals are passively viewing stimuli versus when they are actively performing the task and storing representations of the stimuli in their WM. We therefore applied a two-way ANOVA to compare the neural responses of neurons between the active and passive spatial tasks after the monkeys had been trained to perform the active spatial task. We ultimately observed a small but not significant increase in the proportion of cells that coded matching status during the sample period, as well as an increase in the proportion of cells coding sensory information in the delay1 period when the animal was prompted to report the matching decision (passive proportion = 9.3%, active proportion = 11.7%, exact matched pair proportion test, F = 1.385, p = 0.362) (Fig. 7A). Interestingly, a large proportion (CS: 81.8%, NMS: 52.2%) of cells changed their selectivity category across tasks, especially for CS cells (Fig. 7B), and the degree of NMS does not seem to be predictive of whether a given neuron would fall in the same selectivity category in both tasks (Fig. 7C).

Figure 7.

Cell selectivity in tasks with the same sensory input but different behavioral requirements. Analyses were performed on neural data from the same population of cells, with matching number of trials in the passive and active spatial tasks. Only trials that had the exact same stimuli pairs in both tasks were included in this analysis. A, Examining interaction (NMS) between stimulus preference and matching status. Bar graphs represent the proportions of cells tuned to stimuli location, trials matching status, and their interaction in different stages of the tasks. Pie charts represent the proportion of different selectivity categories (NS, CS, LMS, and NMS) in the sample period. B, Flow diagram represents cell selectivity category mapping cross tasks. On the left side of each plot, cell selectivity category (NS, CS, LMS, and NMS) in the passive task was color-coded. The thickness of lines represents the number of cells. On the right side of each plot, cells belonging to different selectivity categories in the active spatial task were clustered together, so the composition of cell selectivity category with reference to the other task is shown by proportion of different colored lines. C, F scores of the interaction term in the ANOVA were compared between cells that were classified as NMS cell in both tasks (overlapping cells) and those only classified as NMS in one of the tasks (nonoverlapping cells).

Information encoding by NMS neurons

Prior research has demonstrated that training leads to increases in both persistent activity and the incorporation of task-relevant information in neural populations, and these effects were more pronounced during the delay2 period in our task (Meyers et al., 2012). We therefore wished to test whether the increase of neurons exhibiting NMS would be greater in the second delay interval, as well. The current study revealed that this was not the case (delay 2 in Fig. 3A–B). The result suggests that the plasticity involving the increase in delay period activity and the increase in the magnitude of NMS are independent of each other.

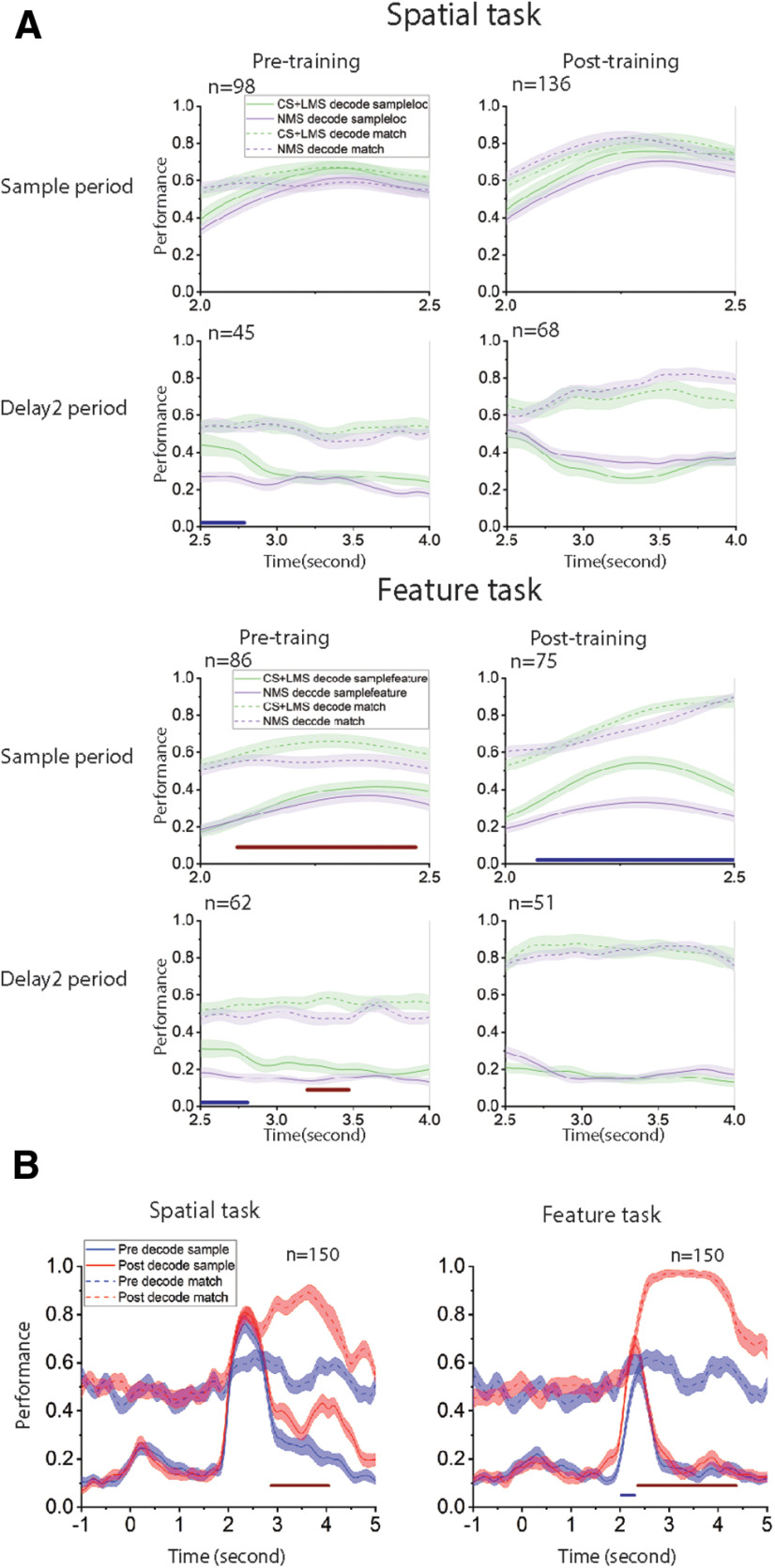
We also investigated the relative contribution of NMS to encoding new task information. We used a linear SVM decoder to decode sensory information (location and shape) and match/nonmatch status information to quantify the amount of task-relevant information contained in linear (CS and LMS) and NMS cells (Fig. 8). Since the cell selectivity category could be defined by their response in either sample or delay2 period, we randomly selected equal numbers of linear and nonlinear cells in both task epochs for each comparison. The random selecting process was repeated multiple times to obtain a CI. We ultimately found that linear and nonlinear cells contain comparable amounts of linearly decodable information in regard to both sensory information and task-relevant information (Fig. 8A). The only observed difference between the decodable information in the linear and nonlinear cells occurred in the post-training feature task, where linear cells were observed to contain more stimulus information (mean performance 46.6% for CS, 29.6% for NMS during sample period) in the sample period.

Figure 8.

A, Decoding task variables with an equal number of linear (CS+LMS) and nonlinear cells (NMS), at different task epochs and training stages. The selectivity categories (CS, LMS, and NMS) were defined by spiking count in corresponding epochs (sample and delay2) with reference to selectivity to stimuli identity (stimuli location or shape) and matching status. Decoding performance for different task epoch and training stage combinations are displayed in separate subplots. In each subplot, the y axis represents decoding performance, with results for stimuli identity and matching status represented by solid and dashed line, respectively. Cell selectivity categories are color-coded (green represents CS+LMS; purple represents NMS). Numbers on the x axis represent time relative to onset, with the sample period occurring from 2 to 2.5 s, and delay2 period occurring from 2.5 to 4 s. Red bars under each subplot represent the time points when the decoding performance for the matching status differs significantly between linear and nonlinear cells. Blue bars under each subplot represent the time points when the decoding performance for the sample stimulus identity differs significantly between linear and nonlinear cells. For the spatial task, we found that, despite the significant change in proportion of NMS cells after training, NMS does not seem to represent increased quantities of linearly decodable information per cell compared with linear cells. For the feature task, linear cells are generally more selective in many conditions, especially when coding stimuli identity after training in the active task. B, Incorporation of new information after training for the spatial and the feature tasks. Linear SVM decoders were trained to classify either stimulus identity or matching status with z score-normalized pseudo-population response. Color bars represent time points when the performance for NMS and linear cells differs significantly: red bars represent decoding matching status; blue bar represents decoding stimuli identity.

We applied cross temporal decoding to compare classical and linear mixed cells with regard to population coding dynamics during the delay period. If information were represented by a stable pattern of activity, the classifier trained at one time point would be expected to work equally effectively at other time points where the information is present. Conversely, if information were represented by dynamic patterns of activity; then the decision boundary at one time point would not contribute to decoding information at other time points. The most prominent result from this analysis is that NMS cells produced significantly more stable code for matching information in the spatial task, compared with CS and LMS cells, as indicated by higher performance off the diagonal during the delay2 period (Fig. 9). The contrast between the CS+LMS versus NMS cells supported the idea that NMS is particularly important for downstream readout. A stable code is generally easier to read-out, since it does not require the downstream circuit to track the time elapsed to decode information. In the context of our task, the sensory information is no longer necessary during the delay2 period for the behavioral response, posing a likely explanation for why only the code for match/nonmatch information is stable in the delay2 period for NMS cells. Importantly, this stability was not observed in CS+LMS cells, despite the matching status also being represented in these cells. Another intriguing and related phenomenon revealed by our decoding analysis (Fig. 8B) is that stimulus information could be decoded above chance level for the spatial, but not the feature task in the delay2 period, although, as noted, maintenance in memory of either the first or second stimulus is no longer necessary at this stage. This supports the idea that PFC processes the spatial and shape information differently in the regions we recorded from.

Figure 9.

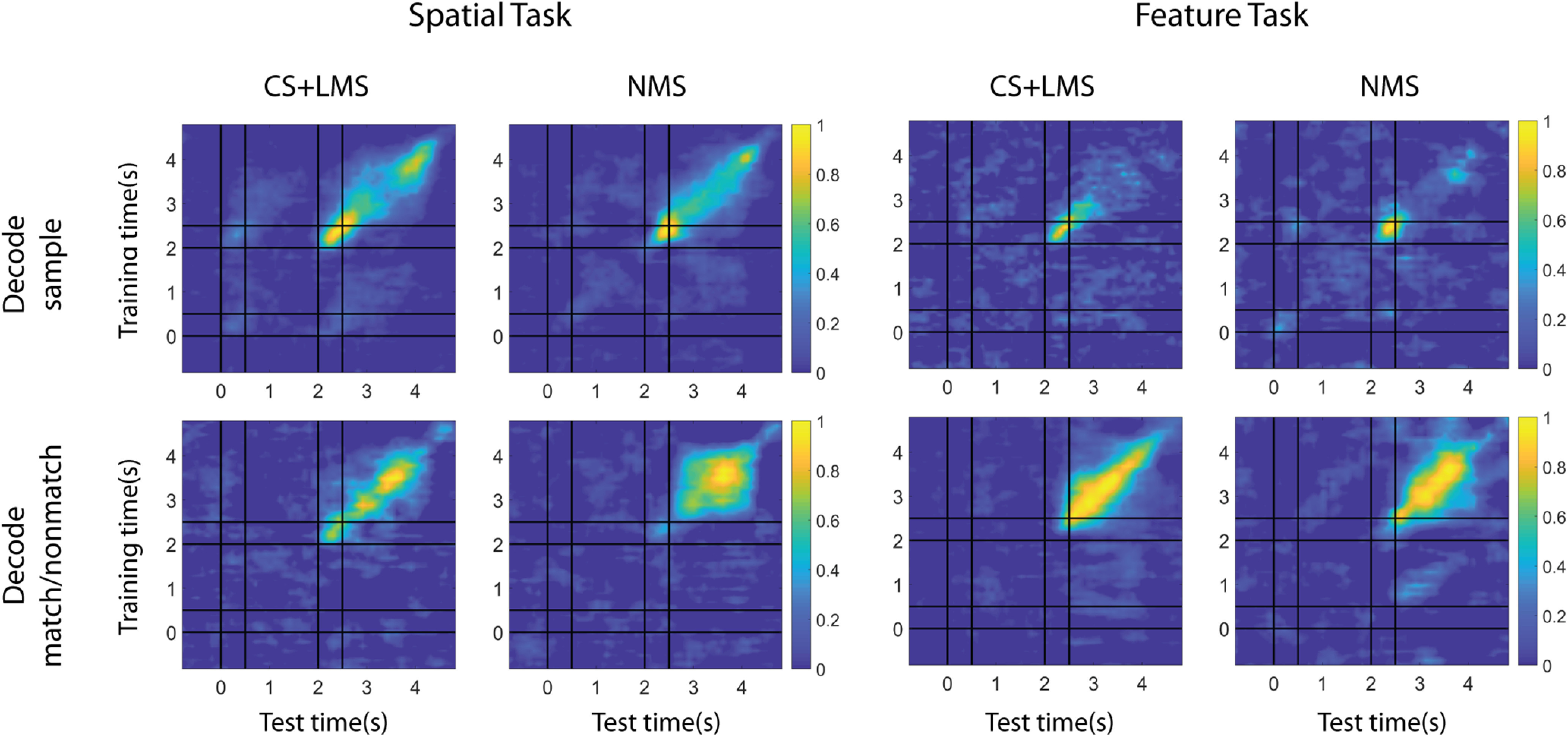
Coding dynamics of pure and linearly selective cells (CS and LMS) versus NMS cells. Linear kernel SVM decoders were trained to perform cross-temporal decoding with different selectivity populations in the delay2 period, for both spatial and feature tasks, as indicated by the y axis. The decoder was then required to predict whether a match or nonmatch occurred at each time point based on a different test set of data, as indicated by the x axis. Normalized decoding accuracy is indicated in the color bar, demonstrating how spatial and feature WM representations can be decoded from specific patterns of neural activity. Coding of matching information for NMS cells is more stable across time for the spatial task.

NMS in correct and error trials

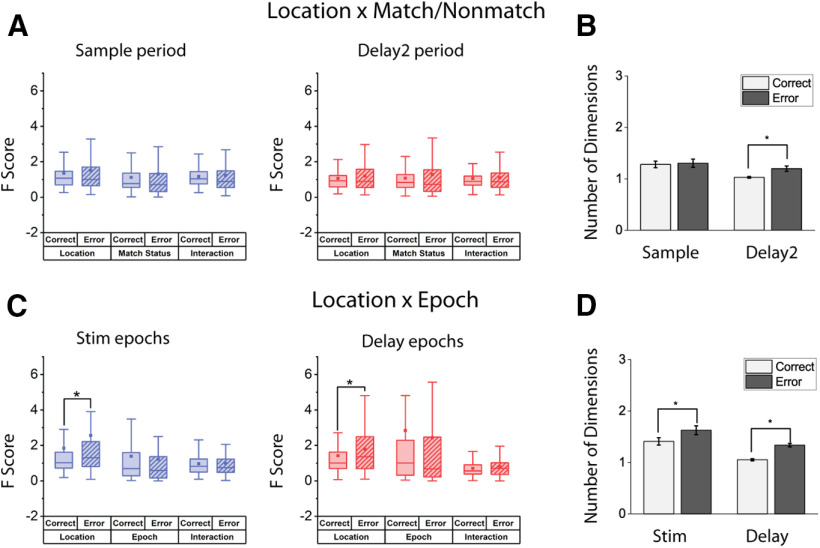
The presence of decodable information in the PFC does not necessarily imply that the information is used by the subjects to guide behavior. In order to decipher the role of NMS in guiding behaviors, we examined the F score of the main effects and their interaction in the ANOVA test in correct versus error trials for the spatial task (Fig. 10A,C), which displayed higher NMS levels than the feature or conjunction tasks. Similar to the pretraining versus post-training comparisons, we examined two types of mixed selectivity: stimulus location versus matching status and stimulus identity versus task epoch. The number of trials and task variables were matched for each cell to avoid confounds in the comparison. The mean F score in for the location variable in the stimulus epochs for the location × epoch comparison was equal to 1.86 for correct trials, and 2.59 for error trials (paired t test, t₍₁₄₇₎ = 3.38, p = 9.42 × 10⁻⁴). The effect extended into the delay epochs, where the average F score for location in correct trials was 1.43, and that of error trials was 1.79 (paired t test, t₍₁₅₀₎ = 2.61, p = 0.010). However, we did not find any differences in the F score for the interaction terms in any comparison. The increased F score in error trials for stimuli location may reflect higher variability in error trials in coding or maintaining corresponding information. Alternatively, the increased F score may reflect erroneous association of a combination of conditions. In either case, however, dimensionality collapse does not seem to be the primary cause of errors. A direct measurement of neural response dimensionality revealed that error trials with the most observed NMS did not undergo a decrease of dimensionality (active spatial task; Fig. 10B,D).

Figure 10.

A, C, Comparison of cell selectivity in correct and error trials in the same population for the spatial task, after controlling for trial number and location pairs used. Two forms of mixed selectivity were examined (location × matching, location × task epoch). No change (location × matching delay2 period) or increase (location × task stim and delay epochs, location × matching sample period) in the mean F score of the interaction term of ANOVA results from all recorded cells were observed. Higher F score for the variable of stimuli location was observed in error trials in the location × Epoch comparison. Box boundaries represent 25%-75% data range. Whiskers indicate 1.5 IQR. Squares represent means across cells. B, D, Dimensionality measure for the correct and error spatial task dataset, with different definitions of mixed selectivity: Left, B, location × match/nonmatch; D, location × Epoch. No decrease of dimensionality was found in error trials. * represents p < 0.05.

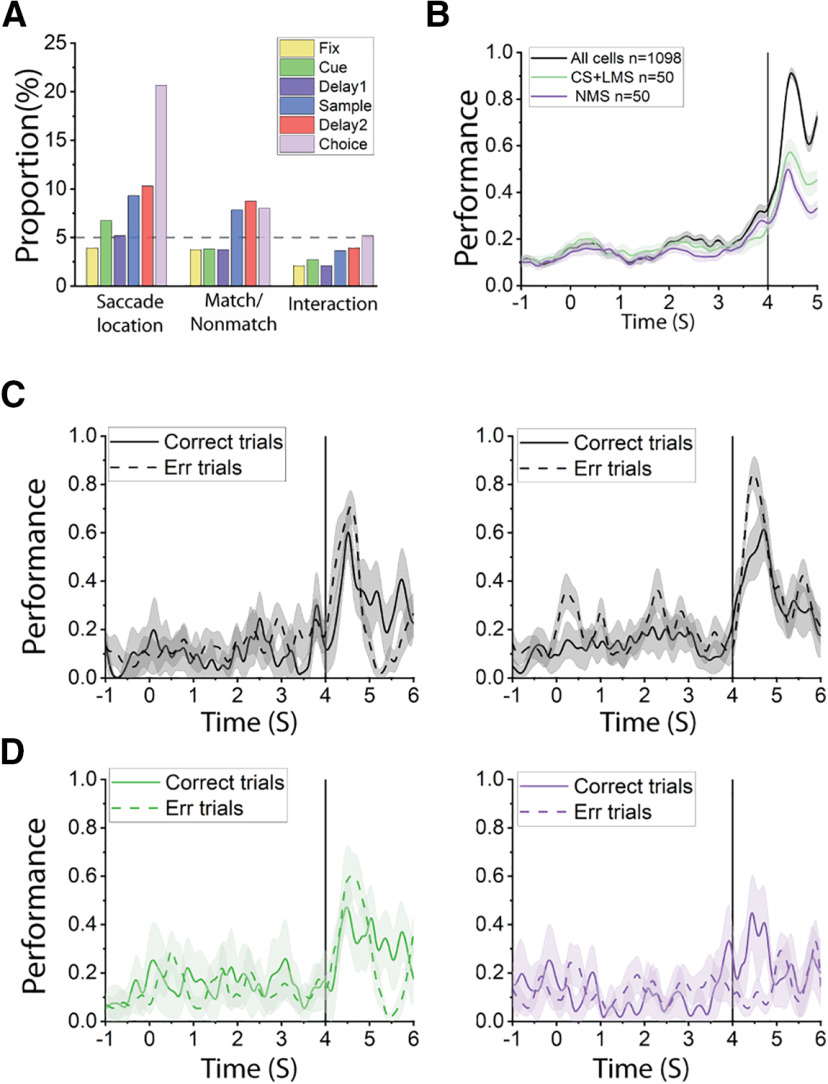
Our analyses above reveal no obvious decrease of NMS representing stimulus identity and match status in error trials. However, to determine whether NMS may be involved with converting match status to action in our task, we decoded saccade direction from correct and error trials by defining different types of selectivity (CS, LMS, NMS) through the same method we used for the sample and delay2 period. Although there was strong selectivity for saccade locations, we ultimately found very little NMS for saccade direction and matching status (Fig. 11A–B). If neurons exhibiting NMS (now defined by the interaction of saccade location and match status) could predict erroneous saccade direction more effectively, we might be able to conclude that NMS plays an important role in behavior, despite the lack of dimensional collapse for stimuli presentation and delay error trial representations of stimuli identity and matching status. However, our results ultimately failed to indicate a significant decrease of such NMS in error trials, either (Fig. 11C–D).

Figure 11.

A, Bar graphs represent the proportions of cells tuned to saccade location, matching status, and their interaction (i.e., NMS) in different stages of the task trials, for the active spatial task. B, Decoding of saccadic direction using all recorded cells, or the same number of CS+LMS/NMS cells in the active spatial tasks. Time 0 at the x axis indicted the onset of the cue. Black line indicates onset of choice array. C, Saccadic direction decoding was equally effective in correct and error trials, regardless of pseudo-population size. Left, Decoding saccadic direction using 239 cells with 4 randomly selected correct and error trials (2 trials in 2 the same 2 conditions are randomly selected, thus resulting in 4 trials for each cell; condition was defined by saccade location × matching status). Right, Decoding saccadic direction using 155 cells with 2 correct and error trials in the same conditions. D, Decoding saccadic direction using different populations from the same cells in C. Left, Decoding performance using 54 CS+LMS cells with 4 correct and error trials. Right, Decoding performance using 10 NMS cells with 4 correct and error trials. In all panels, the shaded range represents 95% CI for 10 randomly constructed pseudo-populations. Time point 0 is the onset of cue. Black line at 4 s indicates the onset of the choice array.

Discussion

Selectivity for different types of information is critical in representing the plethora of stimuli and task contexts that can be maintained in WM. NMS is thought to be critical in that respect, as it allows efficient representation of flexible, arbitrary combinations of variables (Buonomano and Maass, 2009; Rigotti et al., 2010; Barak et al., 2013; Fusi et al., 2016; Johnston et al., 2020). Consistent with this idea, increased dimensionality in NMS has been highlighted as a potential means of increasing the efficiency of WM task performance (Rigotti et al., 2013; Johnston et al., 2020) while dimensional collapse characterizes task errors (Rigotti et al., 2013). Moreover, all task-relevant information could be decoded from NMS neurons alone, despite their relative scarcity, with decoder accuracy actually increasing as the task became more complex (Rigotti et al., 2013). NMS is assumed to emerge with training in complex tasks that combine multiple types of information, or in multiple tasks, even without an explicit requirement to combine such information (Lindsay et al., 2017; Johnston et al., 2020). However, this idea has not been tested experimentally until now. Our study, by virtue of analyzing neural recordings before and after training in a series of cognitive tasks, directly tested these postulates. We found that NMS resulted in a modest increase with training, but only for some tasks; furthermore, task complexity was not a predictor of NMS emergence. A causal relationship between success and dimensionality—and by extension, NMS—was also not supported by our results, as we did not observe any significant changes in NMS between error and correct trials. These insights refine and qualify the role NMS plays in WM, and identify a number of open questions.

Effects of training on neural responses

WM is considerably plastic; and at least some aspects of it, such as mental processing speed and the ability to multitask, can be improved with training (Klingberg et al., 2002, 2005; Bherer et al., 2008; Jaeggi et al., 2008; Dux et al., 2009). WM training has been proven particularly beneficial for clinical populations (e.g., in the case of traumatic brain injury, attention deficit hyperactivity disorder [ADHD], and schizophrenia) (Klingberg et al., 2002; Westerberg et al., 2007; Subramaniam et al., 2012). However, the verdict of whether WM training confers tangible benefits on normal adults, and whether these benefits transfer to untrained domains, remains a matter of heated debate (Fukuda et al., 2010; Owen et al., 2010; Cortese et al., 2015; Schwaighofer et al., 2015; Constantinidis and Klingberg, 2016; Peijnenborgh et al., 2016).

This malleability of cognitive performance is thought to be mediated by the underlying plasticity in neural responses, most importantly within the PFC (Constantinidis and Klingberg, 2016). In a series of prior studies, we have investigated changes in PFC responsiveness and selectivity (Meyer et al., 2011, 2012; Qi et al., 2011; Riley et al., 2018), as well as other aspects of neuronal discharges, such as trial-to-trial variability and correlation between neurons (Qi and Constantinidis, 2012a,b). This led to our present analysis where, guided by experimental and theoretical predictions (Rigotti et al., 2013), we examined NMS as another potential source of enhanced ability to represent WM information after training.

In agreement with our hypothesis, we found that training increased the proportion of neurons that exhibit NMS. However, training does not seem to be a prerequisite, as NMS was also observed in animals that were naive to any cognitive training. Prior research has established that the human and primate PFC represent stimuli in memory even when not prompted to do so (Foster et al., 2017), or without training in WM tasks (Meyer et al., 2007). Our finding of NMS neurons in naive monkeys provides another example of that principle. However, NMS only increased for certain types of task information and not for others. Task variables mixed significantly more with spatial over shape information, thus suggesting that the role of NMS is not universal for all types of working memory. Considering the fact that the spatial information in the current study is largely nonoverlapping and low dimensional (stimulus identities could be represented by one or two numbers), while the shape information is relatively high-dimensional, one possible explanation of the observed difference is that the distinction in the degree of NMS may reflect the qualitatively different ways of representing information with different dimensionality in working memory. In any case, our results suggest that NMS may not be as ubiquitous as previously believed, across all tasks, all prefrontal areas, and individual subjects. These results are consistent with some prior studies that have also failed to uncover substantial NMS in the tasks they used (Cavanagh et al., 2018). Examining where NMS failed to appear, and where WM representations fail to spontaneously appear, will be an important area of future investigation for NMS.

The greatest increase in the proportion of neurons that exhibited NMS for the spatial working memory task was observed at the mid-dorsal region during the sample presentation period (Fig. 5). This disproportionate increase in NMS neurons was associated with a modest decrease in neurons that exhibit CS, as predicted by theoretical studies (Lindsay et al., 2017). However, this finding, too, did not generalize across conditions. During the delay periods of the spatial task, we saw an across-the-board increase in neurons with CS, which were much more abundant in the trained than the naive PFC (Fig. 3). Indeed, the increase of encoding of matching information in the feature task after training was driven almost exclusively by CS cells, suggesting a potential division of labor between NMS and CS in the PFC for different types of information.

Task complexity and difficulty

Another potential factor that determines the emergence of NMS is task complexity. NMS may arise exclusively in highly complex tasks that require subjects to maintain and combine multiple types of information in their WM, simplifying the involved neural circuits to achieve greater efficiency (Rigotti et al., 2013). We thus tested this concept by applying a dataset that relied on three tasks which differed in complexity (and overall difficulty). The spatial and feature tasks each required maintenance of a single stimulus property in memory (location or shape). The conjunction task required both. Surprisingly, however, we did not observe a higher incidence of NMS in the conjunction task compared with the feature task. Moreover, we observed a much lower incidence of NMS in the feature task compared with the spatial task despite the fact that the latter was no more complex or difficult for the monkeys to perform (Meyer et al., 2011; Riley et al., 2018). This implies that NMS in the PFC may not be necessary for certain types of information, such as object shape, even when the task complexity is high. Our tasks required modest flexibility for stimulus representations: presentation of two stimuli in sequence requires choice of the green or blue target depending on their relative location, shape, or location-shape combination. However, the flexibility of the task was bounded by the fact that the same basic match/nonmatch rule applied across all tasks. It is possible that a task that required more flexible representation (e.g., if the monkeys were additionally cued in each trial to select the green choice target for either the match or the nonmatch) would result into emergence of even more neurons with mixed selectivity. Future research is therefore necessary to assess this possibility.

Regional specialization

Different types of information are represented across the dorsoventral and anterior-posterior axes of the PFC (Constantinidis and Qi, 2018), and examining the regional distribution of NMS neurons within the PFC therefore bears a clear importance. We found that NMS was most strongly demonstrated in the mid-dorsal area for the spatial task and the posterior dorsal area for the feature task. The specialization of different PFC subregions in processing location versus feature information is still a topic of debate. Current evidence suggests that the degree of specialization may depend on what stimuli are used. For highly specific stimuli that require within-category discrimination, such as faces, the selective cells are clustered in anatomically defined patches in the ventral PFC (O'Scalaidhe et al., 1997, 1999), while for more general stimuli varying in shape and color, the coding seems to be distributed in both the dorsal and ventral portions of the PFC (Rao et al., 1997; Meyer et al., 2011; Kadohisa et al., 2015). In the current study, we used simple geometrical shapes to probe the selectivity for feature, and we sampled from both dorsal and ventral portion of PFC. It is noticeable that, in the current study, the encoding of spatial information is stronger compared with feature information in the sampled neurons. This is in agreement with previous reports that the degree of selectivity is stronger on a single-neuron level for location compared with simple geometrical shapes in the dorsal portion of the PFC (Constantinidis and Qi, 2018).

Information content and task performance

A critical issue regarding the role of mixed selectivity is whether nonlinear mixed selectivity, by virtue of representing information more efficiently, is also more necessary for effective task performance (Rigotti et al., 2013). We relied on a linear SVM decoder to decipher the specific information that may be represented by NMS cells, compared with CS cells. In the current study, we found that similar quantities of information could be decoded from (equal-sized) populations of CS and NMS neurons, although the coding dynamics for some types of information were significantly different between CS and NMS cells. Similarly, when we compared the NMS levels of successful and failed task trials, we were surprised to find that there was no appreciable difference. This suggests that loss of information encoded in a nonlinear manner may not be the primary factor of successful WM-guided behavior. An important caveat for this conclusion is that the combination of small and unbalanced number of error trials in match versus nonmatch conditions makes the detection power for the interaction fairly small in our analysis. Moreover, with very little NMS presented even in correct trials after matching the trial number for the error condition, a floor effect may have prevented a further decline from becoming apparent. Nonetheless, our result reinforces the idea that NMS is not necessary in all tasks, without which performance fails. An interesting observation in this analysis was that the proportion of cells tuned to spatial location was elevated in error trials. The result may imply that task success also depends on the task relevance of the represented information, with error trials incorporating greater quantities of task-irrelevant spatial information and therefore unnecessarily drawing away WM resources without benefit. Ultimately, by comparing and evaluating the conditions in which NMS emerges, we may decipher its true role in WM and other cognitive functions.