Abstract
Background: Understanding the dynamics of the COVID-19 pandemic and evaluating the efficacy of control measures requires knowledge of the number of infections over time. This number, however, often differs from the number of confirmed cases because of a large fraction of asymptomatic infections and different testing strategies.
Methods: This study uses death count statistics, age-dependent infection fatality risks, and stochastic modeling to estimate the prevalence of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) infections among adults (aged 20 years or older) in 165 countries over time, from early 2020 until June 25, 2021. The accuracy of the approach is confirmed through comparison with previous nationwide seroprevalence surveys.
Results: The estimates presented reveal that the fraction of infections that are detected vary widely over time and between countries, and hence confirmed cases alone often yield a false picture of the pandemic. As of June 25, 2021, the nationwide cumulative fraction of SARS-CoV-2 infections (cumulative infections relative to population size) was estimated as 98% (95% confidence interval [CI] 93–100%) for Peru, 83% (95% CI 61–94%) for Brazil, and 36% (95% CI 23–61%) for the United States.
Conclusions: The time-resolved estimates presented expand the possibilities to study the factors that influenced and still influence the pandemic’s progression in 165 countries.
Keywords: COVID-19, SARS-CoV-2, Prevalence, Time series, Infection fatality risk, Exponential growth rate
Background
Accurate estimates of the prevalence of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) in a population are needed to evaluate disease control policies and test strategies, determine the role of environmental factors, predict future disease spread, assess the risk of foreign travel, and determine vaccination needs (Nguimkeu, Tadadjeu, 2021, Pearce, Vandenbroucke, VanderWeele, Greenland, 2020). Even if a retreat of the pandemic seems within reach in many countries, the efficacy of control measures in 2020 and 2021 and the environmental, political, and societal factors that influenced the epidemic’s progression in each country will undoubtedly be the topic of scholarly work for years to come. Because of the existence of a large fraction of asymptomatic cases as well as variation in reporting, testing effort, and testing strategies (e.g., random versus symptom triggered) (Chow et al., 2020), reported case counts cannot be directly converted to infection counts, and a comparison of confirmed case counts between countries is generally of limited informative value (Lachmann et al., 2020). Large-scale seroprevalence surveys (e.g., using antibody tests) can yield information on the disease’s prevalence and cumulative number of infections in a population, either directly or using dynamical modeling (Larremore et al., 2021). However, such surveys involve substantial financial and logistical challenges, and yield reliable prevalence estimates only near the periods covered by the surveys; prevalence estimates based on seroprevalence surveys are thus largely restricted to short periods (e.g., Bogogiannidou, Vontas, Dadouli, Kyritsi, Soteriades, Nikoulis, et al., 2020, Le Vu, Jones, Anna, Rose, Richard, Bernard-Stoecklin, et al., 2021, Merkely, Szabó, Kosztin, Berényi, Sebestyén, C, et al., 2020, Murhekar, Bhatnagar, Selvaraju, Saravanakumar, Thangaraj, Shah, et al., 2021).
In contrast to case reports, COVID-19-related death counts are generally regarded as less sensitive to testing effort and testing strategy (Flaxman, Mishra, Gandy, Unwin, Mellan, Coupland, et al., 2020, Lau, Khosrawipour, Kocbach, Ichii, Bania, Khosrawipour, 2021, Lu, Nguyen, Link, Davis, Chinazzi, Xiong, et al., 2020, Maugeri, Barchitta, Battiato, Agodi, 2020a), and fortunately most countries have established nationwide continuous reporting mechanisms for COVID-19-related deaths. Hence, in principle, knowing the infection fatality risk (IFR; the probability of death following infection with SARS-CoV-2) should permit the conversion of death counts to infection counts (Bohk-Ewald, Dudel, Myrskylä, 2020, Flaxman, Mishra, Gandy, Unwin, Mellan, Coupland, et al., 2020, Lu, Nguyen, Link, Davis, Chinazzi, Xiong, et al., 2020, Sánchez-Romero, di Lego, Prskawetz, L. Queiroz, 2021). The IFR of SARS-CoV-2, however, depends strongly on the host’s age, and hence the effective IFR of the entire population depends on the population’s age structure as well as the disease’s age distribution (Dowd et al., 2020). Indeed, it was shown that the age dependency of the IFR, the age-dependency of SARS-CoV-2 prevalence, and the age structure of the population are largely sufficient to explain variation in the effective IFR between countries (Levin et al., 2020). This suggests that age-stratified death counts (or estimates thereof) should be used in conjunction with age-dependent IFRs to obtain an accurate estimate of infection counts. This approach has been successfully used to estimate SARS-CoV-2 prevalence over time in Europe until May 4, 2020, on the basis of reported age-stratified death counts (Flaxman et al., 2020). In principle, one could also first determine the “effective” IFR (integrated over all ages) for the entire population and combine that effective IFR with total (non-age-stratified) death counts to estimate infection rates. This approach was taken by Sánchez-Romero et al. (2021), who first estimated the effective IFR for various states in the United States on the basis of—among other factors—age-specific mortality data and then estimated the cumulative number of SARS-CoV-2 infections across the United States as of September 8, 2020. However, such an effective IFR is specific to the population for which it was estimated, and hence applying it to other countries—even if corrections are made for the local population age structure, which is possible in the framework of Sánchez-Romero et al. (2021)—would fail to account for differences (or uncertainty) in the age distribution of infections or deaths.
Unfortunately, age-stratified and time-resolved death statistics are not readily available for many countries with insufficiently comprehensive reporting, thus preventing the direct adoption of the above-mentioned approaches (Flaxman, Mishra, Gandy, Unwin, Mellan, Coupland, et al., 2020, O’Driscoll, Ribeiro Dos Santos, Wang, Cummings, Azman, Paireau, et al., 2021). In cases where only total death counts (i.e., aggregated over all ages) are available, such as the ones disseminated by the World Health Organization, one needs to independently estimate the age distribution of deaths (or infections) to convert total death counts to infection counts. Bohk-Ewald et al. (2020) disaggregated nationwide total death counts on the basis of a previously determined global average age distribution of deaths to estimate SARS-CoV-2 infections in 10 countries up to July 23, 2020. However, using a global average age distribution of deaths ignores the fact that the age distribution of infections (and deaths) actually needs to be adjusted for each country’s population age structure, even if any given age group were to experience a similar exposure in each country. Furthermore, while the approaches used by Bohk-Ewald et al. (2020) and Sánchez-Romero et al. (2021) can account for the average time lag between infection and death, they cannot account for its actual probability distribution and considerable spread around the mean (Linton et al., 2020), which further complicates the estimation of time-resolved infections from deaths. Lastly, all of the above-mentioned studies cover only an early portion of the pandemic (Bohk-Ewald, Dudel, Myrskylä, 2020, Flaxman, Mishra, Gandy, Unwin, Mellan, Coupland, et al., 2020) or focus only on a single time point (Sánchez-Romero et al., 2021), and focus on a small number of countries (1–11).
This study addresses the above-mentioned challenges by leveraging information on the age distribution of SARS-CoV-2 infections from multiple countries with available age-stratified death reports to estimate the likely age-distribution of SARS-CoV-2 infections in other countries, while accounting for each country’s population age structure and for uncertainty due to additional unidentified factors. On the basis of these calibrations, national SARS-CoV-2 prevalences (cumulative number of infections, weekly new infections, and exponential growth rate) are estimated over time, while each country’s population age structure, the likely age distribution of infections, the age dependency of the IFR, and the variation in the time lag between infection and death are accounted for. The estimates are specific to adults aged 20 years or older, covering 165 countries from early 2020 until June 25, 2021. The estimates are largely consistent with data from multiple previously published nationwide seroprevalence surveys. Unless mentioned otherwise, in the following, “infection,” “death,” and “vaccination” refer exclusively to SARS-CoV-2 infections, COVID-19-related deaths, and full vaccination against SARS-CoV-2, respectively.
Results and discussion
Calibrating the age distribution of SARS-CoV-2 prevalence
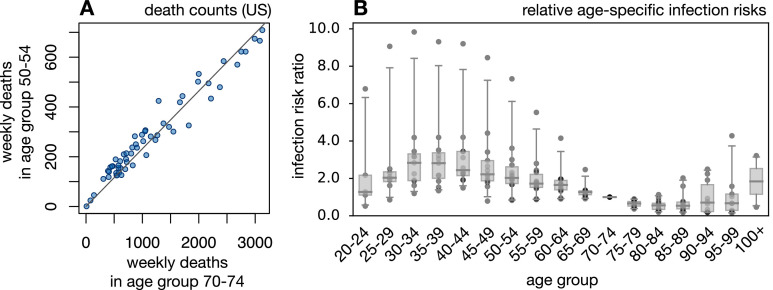
To calculate infection counts solely from total (i.e., non-age-stratified) death counts, while accounting for the age dependency of the IFR and each country’s population age structure, independent estimates of the ratios of infection risks between age groups (i.e., the risk of infection in any one age group relative to any other age group) are needed. To determine the general distribution of age-specific infection risk ratios, this study analyzed weekly age-stratified COVID-19-related death reports from 15 countries around the world using a probabilistic model of Poisson-distributed time-delayed death counts (see “Methods” for details). Briefly, for any given country any given week and any given age group the number of new infections during that week () is assumed to be approximately equal to where represents some fixed reference age group, is the population size of age group and is the relative risk of infection of an individual in age group compared with an individual in age group . The expected number of deaths in each age group 4 weeks later (roughly the average time lag between infection and death; Linton et al., 2020), denoted was assumed to be where is the IFR for that age group. While could, in principle, also differ between countries, to date insufficient information is available for calibrating separately for each country (but see the discussion of caveats below). Age-specific IFRs were calculated beforehand by averaging multiple IFR estimates reported in the literature (Levin, Hanage, Owusu-Boaitey, Cochran, Walsh, Meyerowitz-Katz, Linden, Dehning, Mohr, Mohring, Meyer-Hermann, Pigeot, et al., 2020, O’Driscoll, Ribeiro Dos Santos, Wang, Cummings, Azman, Paireau, et al., 2021, Pastor-Barriuso, Pérez-Gómez, Hernán, Pérez-Olmeda, Yotti, Oteo-Iglesias, et al., 2020, Rinaldi, Paradisi, 2020, Salje, Tran Kiem, Lefrancq, Courtejoie, Bosetti, Paireau, et al., 2020). This calibration thus accounts for the age structure of each country, the age distribution of the disease in each country, and the age-dependency of the IFR. A critical assumption of the model is that, in any given country, nationwide age-specific infection risks covary linearly between age groups over time (i.e., an increase of disease prevalence in one age group coincides with a proportional increase of prevalence in any other age group). This assumption is motivated by the observation that weekly nationwide death counts generally covary strongly linearly between age groups (Fig. 1 A and Supplemental Figs. S1 and S2); the adequacy of this model is also confirmed in retrospect (see below). For each country, the infection risk ratios (for all ) and the weekly infections in the reference age group (one per week) were fitted to the age-stratified weekly death counts by a maximum-likelihood approach and under the assumption that weekly death counts follow a Poisson distribution. This stochastic model explained the data generally well, with observed weekly death counts almost always falling within the 95% confidence interval of the model’s predictions (Supplemental Fig. S3). This supports the initial assumption that infection risks covary approximately linearly between age groups over time and suggests that country-specific but time-independent infection risk ratios are largely sufficient to describe the age distribution of SARS-CoV-2 infections in a country and over time. For any given age group the fitted infection risk ratios differed between countries but were generally of the same order of magnitude (Fig. 1B). On the basis of this observation, and as explained in the next section, it thus seems possible to approximately estimate the number of infections in any other country on the basis of total death counts, the population’s age structure, and the pool of infection risk ratios fitted above (accounting for the uncertainty in the latter due to unknown additional factors).
Fig. 1.
Infection and death rates covary linearly between age groups. (A) Weekly reported COVID-19-related death counts in the United States in the age group from 70 to 74 years (horizontal axis) and the age group from 50 to 54 years (vertical axis). Each point corresponds to a different week (defined here as a 7-day period). The linear regression line is shown for reference. For additional age groups and countries, see Supplemental Fig. S1. The strong colinearity of death rates between age groups suggests that infection risks also covary linearly between age groups. (B) Relative infection risks (relative to the age group from 70 to 74 years) for different countries estimated on the basis of death-stratified COVID-19-related death counts. Each column represents a different age group, and in each column each point represents a distinct country. Horizontal bars represent medians and boxes span 50% percentiles of the data.
Estimating infection counts over time
On the basis of the pool of fitted infection risk ratios, the same age-dependent IFRs as used above, the probability distribution of time lags between infection, disease onset, and death (Linton et al., 2020), and total (non-age-stratified) COVID-19-related death count reports disseminated by the World Health Organization, the weekly infection counts were estimated over time in each of 165 countries that met certain data quality criteria (details are provided in “Methods”). Briefly, for any given country any given week and any given set of relative infection risks the total number of deaths during that week () was assumed to be Poisson distributed with expectation given by
| (1) |
where, as before, is the IFR for age group is the population size of age group is the probability that a fatal infection will result in death after weeks, and are the minimum and maximum considered time lags (in weeks) between infection and death, and is the (a priori unknown) number of new infections in the reference age group during week . For the second sum in Eq. (1), only age groups of 20 years or older were considered (in 5-year intervals) because estimates of the infection risk ratios were unreliable for younger ages (because of low death counts) and because deaths among people younger than 20 years were numerically negligible compared with the total number of deaths reported. The expected number of deaths in any given week depends on the number of infections in multiple previous weeks because of the variability of the time lag between infection and death (typically 2–6 weeks; Linton et al., 2020). Hence, the time series of observed weekly death counts () results from a convolution (“blurring”) of the weekly infections counts (), making the estimation of the latter based on the former a classical deconvolution problem, similar to those known from electronic signal processing, financial time series analysis, or medical imaging (Mendel, 1990, Wiener, 1964). Put simply, deconvolution can be interpreted as an algebraic inversion of the operation of convolution, similar to inverting the matrix of a linear transformation. In contrast to estimation approaches based on fitting dynamical models (e.g., susceptible-infectious-recovered or susceptible-exposed-infectious-recovered models) (Baccini, Cereda, Viscardi, 2021, Chow, Chang, Gerkin, Vattikuti, 2020, Maugeri, Barchitta, Battiato, Agodi, 2020a, Maugeri, Barchitta, Battiato, Agodi, 2020b), which assume a particular dynamical model for the epidemic’s growth and often require a priori knowledge of several model parameters to ensure identifiability, time series deconvolution methods typically do not assume any particular dynamical model. Dynamics-agnostic deconvolution methods, including the ones used here, can thus be applied to more complex epidemiological scenarios with no a priori knowledge of the possible dynamics. A major challenge in deconvolution is to avoid overfitting, which can introduce spurious fluctuations in the estimated infection counts. Here, for every country the unknown were estimated by use of a deconvolution operation based on maximum likelihood. To avoid the risk of overfitting, infection counts were first estimated on a lower-resolution time grid, and then linearly interpolated onto a weekly grid (see “Methods” for details). The total number of new infections among people aged 20 years or older during week was estimated as . Cumulative (i.e., past and current) infection counts were calculated as incremental sums of the weekly infection count estimates. The epidemic’s exponential growth rate over time was subsequently calculated from the estimated weekly infection counts on the basis of a Poisson distribution model and using a sliding-window approach.
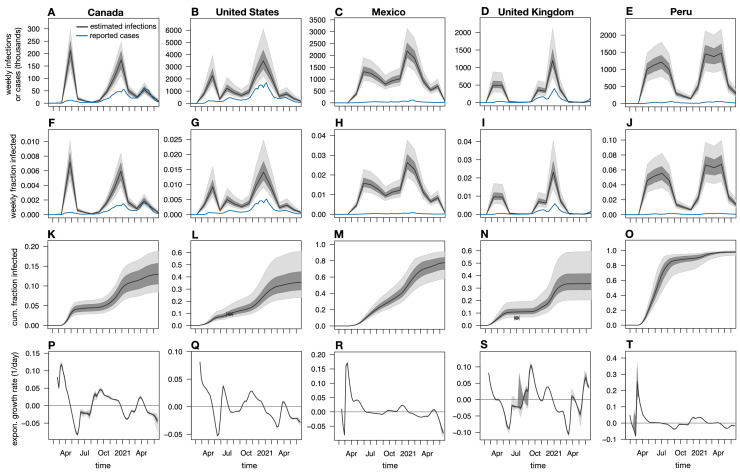
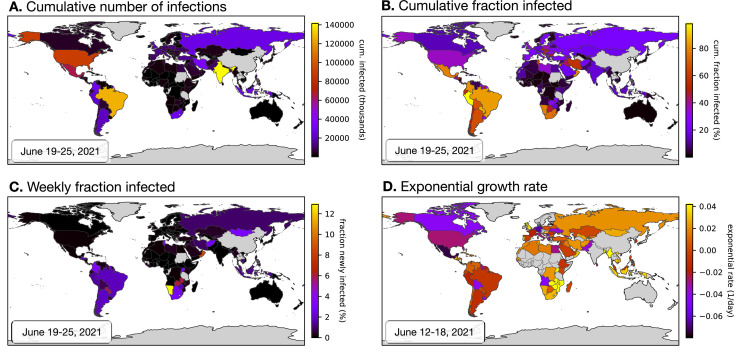
Depending on the particular choice of infection risk ratios, the above approach yielded different estimates for the weekly nationwide infection counts, the cumulative infection counts, and the exponential growth rates over time. Uncertainty in the true infection risk ratios in any particular country stemming from non-modeled additional factors was accounted for by random sampling from the full distribution of fitted infection risk ratios (i.e., obtained from the various calibration countries) multiple times, and calculation of confidence intervals of the predictions based on the obtained distribution of estimates. Estimated weekly and cumulative infection fractions (i.e., relative to population size) and exponential growth rates over time are shown for a selection of countries in Fig. 2 and Supplemental Figs. S4, S5, S6, S7, and S8. A comprehensive report of estimates for all 165 countries is provided as Supplemental File 6. Global color maps of the latest estimates for all 165 countries are shown in Fig. 3 .
Fig. 2.
Estimated nationwide infection rates (adults aged 20 years or older). (A–E) Estimated nationwide weekly number of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) infections over time for Canada, the United States, Mexico, the United Kingdom, and Peru compared with weekly reported cases (blue curves). Black curves show prediction medians, and dark and light shades show the 50th and 95th percentiles of the predictions, respectively. Reported cases are shown 1 week earlier than actually reported (corresponding roughly to the average incubation time; Linton et al., 2020) for easier comparison with infection counts. (F–J) Estimated nationwide weekly fraction of new infections and fraction of reported cases (relative to population size) for the same countries as in A–E. (K–O) Estimated nationwide cumulative fraction of infections (cumulative infections divided by population size) for the same countries as in A–E. Circles show empirical nationwide prevalence estimates from published seroprevalence surveys for comparison (horizontal error bars denote survey date ranges, and vertical error bars denote 95% confidence intervals as reported by the original publications; details are provided in Supplemental Table S1). (P–T) Estimated exponential growth rate based on weekly infection counts for the same countries as in A–E. Horizontal axes are shown for reference. Each column shows estimates for a different country. All model estimates refer to adults aged 20 years or older, while reported cases (blue curves) refer to the entire population. Analogous plots for all 165 countries investigated are provided in Supplemental File 6.
Fig. 3.
Worldwide overview of latest estimates (adults aged 20 years or older). Global map of the latest estimated nationwide (A) cumulative (past and current) number of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) infections, (B) cumulative fraction of infections, (infections relative to population size), (C) weekly fraction of new infections (relative to population size), and (D) current exponential growth rate. Dates of the estimations are given in the lower-right corner of each figure. Countries for which an estimation was not performed (e.g., because of insufficient data) are shown in gray. Analogous world maps for older dates are available in Supplemental File 6.
To assess the accuracy of the approach described above, the estimated cumulative infection fractions were compared with seroprevalence estimates from 22 previously published nationwide seroprevalence surveys across 14 countries (Supplemental Table S1) (Alharbi, Alghnam, Algaissi, Albalawi, Alenazi, Albargawi, et al., 2021, Anand, Montez-Rath, Han, Bozeman, Kerschmann, Beyer, et al., 2020, Bogogiannidou, Vontas, Dadouli, Kyritsi, Soteriades, Nikoulis, et al., 2020, Espenhain, Tribler, Jørgensen, Holm Hansen, Wolff Sönksen, Ethelberg, 2021, Hallal, Hartwig, Horta, Victora, Silveira, Struchiner, et al., 2020, Le Vu, Jones, Anna, Rose, Richard, Bernard-Stoecklin, et al., 2021, Merkely, Szabó, Kosztin, Berényi, Sebestyén, C, et al., 2020, Murhekar, Bhatnagar, Selvaraju, Rade, Saravanakumar, Vivian Thangaraj, et al., 2020, Murhekar, Bhatnagar, Selvaraju, Saravanakumar, Thangaraj, Shah, et al., 2021, Nah, Cho, Park, Hwang, Cho, 2021, Poljak, Oštrbenk Valenčak, Štrumbelj, Maver Vodičar, Vehovar, Resman Rus, et al., 2021, Pollán, Pérez-Gómez, Pastor-Barriuso, Oteo, Hernán, Pérez-Olmeda, et al., 2020, Reicher, Ratzon, Ben-Sahar, Hermoni-Alon, Mossinson, Shenhar, et al., 2021, Snoeck, Vaillant, Abdelrahman, Satagopam, Turner, Beaumont, et al., 2020, Ward, Atchison, Whitaker, Ainslie, Elliott, Okell, et al., 2020). Only surveys attempting to estimate nationwide seroprevalence in the general population (in particular, either using geographically or demographically stratified sampling or adjusting for sample demographics) were included. Agreement between model estimates and seroprevalence estimates was generally good: 16 of the 22 seroprevalence estimates (accounting for the associated 95% confidence interval and the period of the underlying survey) overlapped with the model’s 95% confidence intervals, with three nonoverlaps observed for Brazil, one for Spain, one for the United Kingdom, and one for France (Supplemental Fig. S4). When point estimates were compared (i.e., not accounting for confidence intervals), the relative differences (model estimate minus seroprevalence, divided by seroprevalence) were mostly in the 25–50% range, although particularly high relative differences were found for Brazil (170–180%), one time point in France (464%), and one time point in Greece (348%) (overview in Supplemental Table S1). Apart from the possibility of erroneous model predictions (discussed extensively below), it should be kept in mind that seroprevalence surveys themselves yield only estimates of the cumulative fraction of infected individuals with an associated uncertainty interval, and that this uncertainty interval need not always account for all sources of error. In particular, the deviations of the model from seroprevalence-based estimates may partly be because antibody concentrations in infected individuals (especially asymptomatic ones) can drop over time, rendering many of them seronegative (Bolotin, Tran, Osman, Brown, Buchan, Joh, et al., 2021, La Marca, Capuzzo, Paglia, Roli, Trenti, Nelson, 2020, Long, Tang, Shi, Li, Deng, Yuan, et al., 2020). Thus, previously infected individuals may not all be recognized as such. This would be consistent with the fact that in all cases of major disagreement between model predictions and seroprevalence estimates the former were greater than the latter. Furthermore, sensitivity and specificity estimates for antibody tests performed in the laboratory or claimed by manufactures need not always apply in a community setting (La Marca et al., 2020), thus introducing biases in seroprevalence estimates despite nominal adjustments for sensitivity and specificity.
Case counts alone can yield wrong impressions
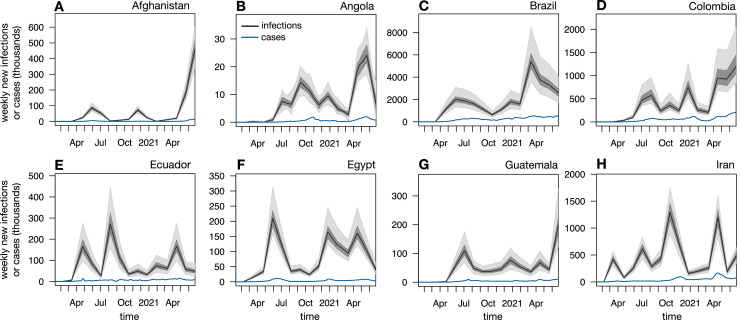
Estimates of SARS-CoV-2 prevalence in a population can yield insight into the epidemic’s scale and growth dynamics that may not have been possible from reported cases alone. One reason is that the fraction of infections that is detected and reported differs greatly between countries and often varies greatly over time. Indeed, according to the present estimates, in most countries, reported case counts initially severely underestimated the actual number of infections and often did not properly reflect the progression of the epidemic, while in many countries more recent case reports capture a much larger fraction of infections and more closely reflect the epidemic’s dynamics (Figs. 2A–E and Supplemental Fig. S5). For example, in the United States, France, Sweden, Belgium, Spain, the United Kingdom, and many other European countries, reported cases reflected only a small fraction of infections occurring in spring 2020, while most subsequent infections were successfully detected. Nevertheless, in many countries, even recent reported case counts poorly reflect the actual dynamics of the epidemic. For example, recent reported cases in Afghanistan, Angola, Brazil, Ecuador, Egypt, Guatemala, and Iran severely underestimate the disease’s rapid ongoing growth, with nearly all infections remaining undetected or unreported (Fig. 4 ). Future investigations, enabled by the infection count estimates presented here, might be able to identify the main factors (e.g., political, financial, and organizational) driving the discrepancies between infections and reported cases, and might be able to suggest concrete steps to eliminate these discrepancies or correct for them.
Fig. 4.
Case counts can suggest drastically different dynamics than infection counts. Nationwide predicted weekly number of new infections (black curves and shades) among adults aged 20 years or older and weekly reported cases (blue curves) for all ages over time in Afghanistan, Angola, Brazil, Colombia, Ecuador, Egypt, Guatemala, and Iran. Black curves show prediction medians, and dark and bright shades show 50% and 95% confidence intervals, respectively. For easier comparison, case counts are shifted backward by 1 week (corresponding roughly to the average incubation time; Linton et al., 2020).
The above observations imply that comparisons of the epidemic’s extent and progression between countries should preferably be done on the basis of infection or death counts, rather than reported cases alone (Flaxman, Mishra, Gandy, Unwin, Mellan, Coupland, et al., 2020, Sánchez-Romero, di Lego, Prskawetz, L. Queiroz, 2021). For example, as of June 25, 2021, the cumulative per-capita number of cases reported for the Czech Republic (16%) and Slovenia (12%) was much higher than for Paraguay (5.8%), Peru (6.3%), or Brazil (8.6%), while the median predicted cumulative infection fractions for the Czech Republic (52%) and Slovenia (38%) were much lower than for Paraguay (86%), Peru (98%; Fig. 2O), and Brazil (83%) (Supplemental Figs. S6 and S7). Similarly, as of June 25, 2021, the cumulative per-capita number of cases reported for the United States (10%) was much higher than for neighboring Mexico (2%), while the median predicted cumulative infection fraction for the United States (36%; Fig. 2L) was much lower than for Mexico (77%; Fig. 2M). These examples highlight the value of considering actual infection counts relative to population size when comparing the extent of the epidemic and its relationship to public policy between countries. Future investigations, enabled by the prevalence estimates presented here, may be able to identify concrete political, environmental, and socioeconomic factors influencing the epidemic’s growth.
Caveats
The predictions presented here are subject to some important caveats. First, erroneous reporting of total COVID-19-related deaths will have a direct impact on the estimated infection counts. This caveat is particularly important for countries with less developed medical or reporting infrastructure (Bastos, Morato, Cajueiro, Normey-Rico, 2021, Feyissa, Tolu, Ezeh, 2021, Galvêas, Barros, Fuzo, 2021, Lloyd-Sherlock, Sempe, McKee, Guntupalli, 2021, Natashekara, 2021, Veiga e Silva, de Andra, dos Santos A. M., de Mattos, Macedo Gomes, Silva Cardoso, et al., 2020), as well as for countries where reports may be censored or modified for political reasons (Kilani, 2021, Kobak, 2021). A general underreporting of total COVID-19-related deaths, as has been suspected, for example, for Brazil (Bastos, Morato, Cajueiro, Normey-Rico, 2021, Veiga e Silva, de Andra, dos Santos A. M., de Mattos, Macedo Gomes, Silva Cardoso, et al., 2020), Italy (Ciminelli and Garcia-Mandicó, 2020), Turkey (Kisa and Kisa, 2020), India (Chatterjee, 2020), and Nigeria (Ohia et al., 2020), would lead to a roughly proportional underestimation of infections. Similarly, inconsistencies between countries and over time in the classification of the causes of death also have the potential to alter model predictions (Feyissa, Tolu, Ezeh, 2021, França, Ishitani, Teixeira, DMXd, Corrêa, Marinho, et al., 2020, Leon, Shkolnikov, Smeeth, Magnus, Pechholdová, Jarvis, 2020, Singh, 2021). For example, it was pointed out that the United States and Russia tend to use rather different criteria for identifying COVID-19 as the underlying cause of death, while Kyrgyzstan and Kazakhstan modified their criteria several months into the pandemic (Singh, 2021). Underreporting of COVID-19-related deaths may also explain why in some rare instances the number of reported positive cases substantially exceeds the estimated number of infections (e.g., for Singapore; Supplemental File 6). Comparisons of results between countries should thus be done with care. In countries where COVID-19-related deaths are suspected of being grossly misreported, excess death rates may provide an alternative means for obtaining accurate COVID-19-related death counts in future analyses (Azofeifa, Valencia, Rodriguez, Cruz, Hayes, Montañez Báez, et al., 2021, Beaney, Clarke, Jain, Golestaneh, Lyons, Salman, et al., 2020, Kobak, 2021).
Second, systematic errors in the age-stratified death counts used for model calibration (obtained from the COVerAGE-DB database; Riffe et al., 2021) could impact model predictions. For example, a potentially more frequent erroneous attribution to alternative plausible causes of death (e.g., other respiratory disorders) in older patients could lead to a relative underreporting of COVID-19-related deaths in older age groups. Such an age bias would lead to an underestimation of the infection risk ratios in older age groups, essentially shifting the estimated age distribution of infections towards younger age groups. If such erroneous calibrations are subsequently used to estimate infections from total death count data, this would lead to an overestimation of infections because the IFR is lower at younger ages (recall that the number of infections is approximately equal to the number of deaths divided by the IFR). Furthermore, while COVerAGE-DB is a rich and robust dataset, its age group harmonizations could, in principle, cause distortions in the age distribution of death counts. To assess whether these distortions are strong enough to substantially influence the model calibrations, in this study calibrations were repeated with an independent dataset of national age-stratified death counts, available for a subset of countries, from the French National Institute for Demographic Studies (INED). Across the two countries covered by both the INED and COVerAGE-DB and satisfying the same data criteria as in the earlier analyses, the infection risk ratios calibrated with the INED data were generally similar to those calibrated with the COVerAGE-DB data (Supplemental Fig. S9).
Third, even if all data were error-free, the infection risk ratios are calibrated on the basis of available age-stratified death statistics from a limited number of countries, and may not apply to all other countries (e.g., because of strong cultural differences). Uncertainty associated with this extrapolation is accounted for by considering infection risk ratios calibrated to multiple alternative countries from multiple continents (see “Methods”).
Fourth, governmental policies implemented at various time points could, in principle, change the infection risk ratios between age groups over time; for example, the opening and closing of schools and universities, or allowing or prohibiting visits to nursing homes. To assess the extent of this possible caveat, here the weekly death counts in each age group were compared with the total (age-integrated) weekly death counts over time (Supplemental Figs. S10 and S2). Age-specific and total death counts correlated strongly linearly over time in nearly all age groups and countries (Pearson correlation coefficient 0.5 or greater in almost all cases), suggesting that in any given country the proportion of infections per age group did not substantially vary over the course of the epidemic. Furthermore, the predictions of the fitted models (which assume time-independent infection risk ratios) were generally highly consistent with the age-stratified death counts (Supplemental Fig. S3), again suggesting that time-independent (but country-dependent and age-dependent) infection risk ratios provide a largely adequate model for the age distribution of infections.
Fifth, age-specific IFRs were obtained from studies in only a few countries (mostly Western) and often based on a small subset of closely monitored cases (e.g., from the Diamond Princess cruise ship). These IFR estimates may not be accurate for all countries, especially countries with a very different medical infrastructure, different sex ratios in the population, or a different prevalence of preexisting health conditions (e.g., diabetes), all of which can affect the IFR. That said, estimated trends over time within any given country, in particular exponential growth rates (e.g., Figs. 2P–T), are unlikely to be substantially affected by such biases if the biases remain relatively constant over time. For example, the exponential growth rates estimated here remained unchanged when alternative IFRs from the literature (Levin, Hanage, Owusu-Boaitey, Cochran, Walsh, Meyerowitz-Katz, Linden, Dehning, Mohr, Mohring, Meyer-Hermann, Pigeot, et al., 2020, O’Driscoll, Ribeiro Dos Santos, Wang, Cummings, Azman, Paireau, et al., 2021, Pastor-Barriuso, Pérez-Gómez, Hernán, Pérez-Olmeda, Yotti, Oteo-Iglesias, et al., 2020, Rinaldi, Paradisi, 2020, Salje, Tran Kiem, Lefrancq, Courtejoie, Bosetti, Paireau, et al., 2020) were considered. To nevertheless examine the robustness of estimated SARS-CoV-2 prevalences against variations in the IFR, the above analyses were repeated with consideration for each age group of a set of multiple IFRs—that is, random sampling from the set of previously reported IFRs (Levin, Hanage, Owusu-Boaitey, Cochran, Walsh, Meyerowitz-Katz, Linden, Dehning, Mohr, Mohring, Meyer-Hermann, Pigeot, et al., 2020, O’Driscoll, Ribeiro Dos Santos, Wang, Cummings, Azman, Paireau, et al., 2021, Pastor-Barriuso, Pérez-Gómez, Hernán, Pérez-Olmeda, Yotti, Oteo-Iglesias, et al., 2020, Rinaldi, Paradisi, 2020, Salje, Tran Kiem, Lefrancq, Courtejoie, Bosetti, Paireau, et al., 2020)—rather than consideration of their mean. Median model predictions remained nearly unchanged; however, the uncertainty (i.e., confidence intervals) of the estimates increased (examples in Supplemental Fig. S11).
Sixth, in countries where a large fraction of the population is now vaccinated, attention should be given to the limitations and interpretation of the model’s predictions for the recent periods of the pandemic. Indeed, while existing vaccines substantially reduce the probability of infection and death, none of them is 100% effective (Bermingham, Morgan, Ayoubkhani, Glickman, Islam, Sheikh, et al., 2021, Calzetta, Ritondo, Coppola, Matera, Di Daniele, Rogliani, 2021, Soiza, Scicluna, Thomson, 2021). Because the IFR may differ between vaccinated and unvaccinated individuals, conversion from death counts to infection counts using IFRs originally determined for unvaccinated people could lead to erroneous infection estimates. This error is relatively small if vaccinated people represent only a small fraction of new infections, which, given that vaccination substantially reduces the risk of infection, is probably the case in the many countries where most of the population is unvaccinated (as of June 25, 2021, 138 of 145 considered countries with available vaccination data; Supplemental File 6). To further assess the implications of vaccination on infection estimates, consider the following back-of-the-envelope calculation. Let be the ratio of vaccinated to unvaccinated individuals, let be the risk of COVID-19-related death for a vaccinated individual relative to an unvaccinated one, and let and denote the number of deaths among vaccinated and unvaccinated individuals, respectively (country and week indices are omitted here for notational simplicity). We have and hence the fraction of deaths attributed to vaccinated individuals is given by
| (2) |
As of June 25, 2021, in nearly all countries most of the population had not been fully vaccinated (hence ), exceptions being the Seychelles, Malta, Israel, Bahrain, Mongolia, Iceland, and Chile (where ranged between 1 and 2.2 on June 25, 2021). Field estimates for vaccine effectiveness against death generally range from 96.7% in Israel (Haas et al., 2021) to 98% in an Italian province (Flacco et al., 2021) and 98.7% in the United States (Vahidy et al., 2021) among fully vaccinated individuals, corresponding to in the range from 0.013 to 0.033. Hence, in nearly all countries (except the Seychelles, Malta, Israel, Bahrain, Mongolia, Iceland, and Chile) vaccinated individuals likely account for less than 3.2% of the reported deaths in recent months (up until June 25, 2021), and even less at earlier stages of the pandemic, where . The infection count estimates presented can thus be interpreted as approximately corresponding to the unvaccinated part of the population (e.g., an estimate of 1000 infections essentially means that among the unvaccinated population there were about 1000 infections), which in turn likely accounts for the vast majority of infections in most countries (as discussed above).
Conclusions
This study presented estimates of the nationwide prevalence and growth rate of SARS-CoV-2 infections over time in 165 countries around the world based on official COVID-19-related death reports, age-specific IFRs, each country’s population age structure, and the probability distribution of time lags between infection and death. The complete report for all 165 countries is provided as Supplemental File 6. These estimates are also provided as machine-readable tables (Supplemental Files 1–5) for convenient downstream analyses; occasionally updated estimates are available at http://www.loucalab.com/archive/COVID19prevalence. Despite a variety of assumptions and caveats, the estimates presented are largely consistent with data from nationwide general-population seroprevalence surveys. The findings presented suggest that while in many countries the detection of infections has greatly improved, there are also numerous examples where even recent reported case counts do not properly reflect the epidemic’s dynamics. In particular, comparisons between countries based on infection counts can yield conclusions very different from those obtained from comparisons based merely on reported cases. The present work thus enables more precise assessments of the disease’s past and ongoing progression, evaluation and improvement of public interventions and testing strategies, and estimation of worldwide vaccination needs.
Methods details
Age-specific IFRs
Age-specific IFRs were calculated on the basis of the following literature: Pastor-Barriuso et al. (2020), Levin et al. (2020), Salje et al. (2020), Rinaldi and Paradisi (2020), O’Driscoll et al. (2021), and Linden et al. (2020). For each age group considered, the average IFR across all of the aforementioned published IFRs was used, after linear interpolation where necessary (Supplemental Table S2).
Calibrating age-specific infection risk ratios
The age-specific infection risk ratios were calibrated as follows. Age-specific population sizes for each country (status 2019) were downloaded from the United Nations website (https://population.un.org/wpp/Download/Standard/CSV) on October 23, 2020 (DESA, 2019). Time series of nationwide cumulative COVID-19-related death counts grouped by 5-year age intervals were downloaded on April 27, 2021, from COVerAGE-DB (https://osf.io/7tnfh), which is a database that gathers and curates official death count statistics from multiple official sources (Riffe et al., 2021). The last 7 days covered in the database were ignored to avoid potential biases caused by delays in death reporting. For each country included in COVerAGE-DB, and separately for each age group, it was ensured that cumulative death counts are nondecreasing (monotonic) over time by linear reinterpolation of death counts at problematic time points. To avoid inaccurate calibrations due to grossly problematic time series, any country for which the strongest violation in monotonicity (the largest decrease of cumulative deaths between any two time points for any age group considered) was greater than 1% of the maximum reported total cumulative deaths in that country (e.g., Canada) was omitted. For similar reasons, countries for which an interpolation was needed (either because of missing data or because of a violation of monotonicity) in any considered age group over a time span greater than 5 weeks (e.g., Iceland) were also omitted.
The remaining monotonized time series of cumulative deaths were linearly interpolated onto a regular weekly time grid (i.e., in which adjacent time points are 7 days apart); no extrapolation was performed (i.e., only dates between the first and last available data points were included). The weekly number of deaths in each age group was calculated as the difference in cumulative deaths between consecutive time points on the weekly grid. While some of the input time series are available at a daily resolution, a weekly discretization was chosen here (a) to reduce time series noise and (b) to “average out” the hard-to-model systematic variations in the epidemic’s dynamics between different days of the week (e.g., weekends vs. workdays). To ensure high accuracy of the calibrated infection risk ratios, only countries for which COVerAGE-DB covered at least 20 weeks with at least 100 reported deaths each were subsequently considered.
For each considered country the “reference” age group was set to the age group that had the highest cumulative number of deaths. Designation of a reference group is done mostly for notational simplicity and consistency, so that age-specific prevalence ratios can all be defined relative to a common reference. For each other age group the infection risk ratio (i.e., the probability of an individual in group being infected relative to the probability of an individual in group being infected) was estimated by use of a probabilistic model. According to this model, the number of deaths in group during week (denoted ) was Poisson distributed with expectation
| (3) |
where is the population size of age group in country and is the IFR for age group . Under this model, the maximum-likelihood estimate for (i.e., given the weekly death count time series) is given by
| (4) |
To avoid errors due to sampling noise, only weeks with at least 100 reported deaths were considered in the sums in Eq. (4). This threshold was chosen as a reasonable compromise between data quality (requiring more deaths per week implies less sampling noise) and data quantity (requiring fewer deaths per week increases the number of weeks available for calibration). Further increasing this threshold to 200 deaths per week generally had negligible effects on the results (see examples in Supplemental Fig. S12). Note that might alternatively be estimated as the slope of the least-squares linear regression:
| (5) |
Estimates obtained via linear regression were nearly identical to those obtained with use of the aforementioned Poissonian model, suggesting that the estimates are not very sensitive to the precise assumed distribution.
To evaluate the model’s adequacy (explained below), this study also estimated the weekly number of infections in the reference age group, via maximum likelihood based on a probabilistic model in which was Poisson distributed with expectation
| (6) |
Under this model, the maximum-likelihood estimate for is given by
| (7) |
To evaluate the adequacy of the above stochastic model in explaining the original death count data, multiple hypothetical weekly death counts were simulated for each age group, and the distribution of simulated death counts was compared with the distribution of true death counts. Specifically, for each country week and age group 100 random death counts () were drawn from a Poisson distribution with expectation
| (8) |
Median simulated death counts and 50% and 95% equal-tailed confidence intervals, along with the original death counts, are shown for various countries and age groups in Supplemental Fig. S3, from which it can be seen that the model’s simulated time series are largely consistent with the original data.
In the subsequent analyses, only infection risk ratios for which the corresponding linear curve (Eq. 5) achieved a coefficient of determination () greater than 0.5 were used (shown in Fig. 1) to avoid less accurately estimated infection risk ratios (typically obtained from countries with low death rates). Infection risk ratios meeting this quality threshold cover 15 countries: Argentina, Bangladesh, Brazil, Colombia, the Czech Republic, Germany, the United Kingdom, Hungary, India, Mexico, Paraguay, Peru, the Philippines, Ukraine, and the United States.
Estimating infection counts from total death counts
Time series of total (non-age-stratified) nationwide cumulative reported death and case counts were downloaded from the website of the World Health Organization (https://covid19.who.int/table) on July 20, 2021. The last 7 days covered in the database were ignored to avoid potential biases caused by delays in case and death reporting (Lipsitch et al., 2015). Cumulative death and case counts were made nondecreasing and interpolated onto a weekly time grid as described above. Only countries that reported at least one death per week for at least 10 weeks were included in the analysis below. In addition, any country for which the strongest violation in monotonicity was greater than 1% of the maximum reported total cumulative deaths in that country, or for which an interpolation was needed (e.g., because of missing data) over a time span greater than 5 weeks (as done above for the COVerAGE-DB data), was omitted. For each country each week and any particular choice of age-specific infection risk ratios (uniquely covering all ages 20 years and older), the number of infections was estimated as follows. Let be the number of consecutive weeks for which total deaths are reported. Let denote some fixed reference age group relative to which infection risk ratios are defined (i.e., such that ); here, ages 70–74 years were used as a reference. Let denote the probability that a fatal infection will lead to death after weeks, where where is the minimum and is the maximum time lag considered. Let . Let be the (a priori unknown) number of new infections occurring during week in the reference age group. The number of COVID-19-related deaths during week in age group denoted was assumed to be Poisson distributed with expectation given by
| (9) |
The total number of deaths in week is thus Poisson-distributed with expectation
| (10) |
As explained earlier, only age groups 20 years and older were included because infection risk ratios could not be reliably estimated for younger ages and because the contribution of younger ages to total death counts can be considered numerically negligible. The were calculated through 1,000,000 Monte Carlo simulations based on the log-normal distribution models fitted by Linton et al. (2020, Table 2) for the time lags between infection and disease onset and the time lags between disease onset and death, and under the assumption that the two time lags are independently distributed (see Supplemental Table S3). The minimum and maximum time lags considered were weeks and weeks because this range covers the bulk (approximately 90%) of cases and because further increasing or decreasing increases the width of the convolution kernel, thus increasing the risk of introducing spurious fluctuations in the estimated . The considered were normalized to have sum 1 to maintain consistency with the total IFR (i.e., summed over all time lags).
Given the above model, the goal is to estimate the unknown weekly infection counts in the reference group, from the recorded weekly death counts, . This is a classical deconvolution problem because each results from the additive effects of infections from multiple preceding weeks (Mendel, 1990, Wiener, 1964). Eq. (10) can be written abstractly in matrix form:
| (11) |
where is a convolution matrix of size
| (12) |
is a column vector of size listing the reported weekly death counts and is a column vector of size listing the unknown weekly infection counts . For notational simplicity, the country index is omitted from and but keep in mind that and refer to a specific country. It is straightforward to show that, under the above model, the log-likelihood of the observed weekly death counts () is given by
| (13) |
In principle, one could estimate the unknown vector via maximum likelihood. Indeed, the above log-likelihood is maximized when the following condition is met:
| (14) |
for all . A sufficient condition for Eq. (14) is that ; in other words, any vector satisfying is a maximum-likelihood estimate. Such an estimate can be obtained using the Moore-Penrose pseudoinverse of denoted (Moore, 1920, Penrose, 1955). Because has linearly independent rows, its pseudoinverse is and hence setting would satisfy . However, because of known issues with inverting convolution matrices, such a naive estimation tends to introduce spurious fluctuations in the estimated . One approach is to reduce the temporal resolution of the estimated which effectively reduces the number of estimated free parameters (Louca et al., 2019). Hence, instead of estimating separately for each week, a coarser time grid was considered that has 4 times fewer time points than the original weekly time grid (i.e., such that the infection count is freely estimated only every fourth week), while assuming linear variation between these time points. This approach is a variant of constrained deconvolution using spline functions, pioneered by Verotta (1993) and reviewed by Madden et al. (1996), using linear splines and maximizing the likelihood function (thus accounting for the Poisson model described above) rather than minimizing the sum of squared residuals (which assumes normally distributed data). For example, for an original weekly time series spanning 100 weeks, first the are estimated at about discrete time points, each 4 weeks apart, and then linear interpolation is used to obtain the remaining . Denoting by the column vector listing the infection counts on this coarser time grid (), and by the matrix mapping to via linear interpolation (i.e., ), one thus obtains the following log-likelihood in terms of :
| (15) |
The corresponding maximum-likelihood estimate can no longer be obtained simply by solving the equation because this linear problem is overdetermined (i.e., it is unlikely that a can be found such that is exactly satisfied). However, an optimally approximate solution (in the least-squares sense), can be obtained by setting . To determine the exact maximum-likelihood estimate —that is, the maximizing in Eq. (15)—numerical optimization was used, as implemented in the R function nloptr::nloptr, while the aforementioned approximation was used as a starting point. Subsequently setting yielded an estimate for the weekly infections counts . The corresponding total number of weekly infections, can be calculated from the estimates as follows:
| (16) |
The corresponding cumulative number of total infections up until any given week can be obtained by summing the weekly infection counts.
Exponential growth rates over time were estimated from the weekly infection counts by a sliding-window approach, as follows. In every sliding window (spanning 5 consecutive weeks), an exponential function of the form was fitted, where denotes the time in days and and are unknown parameters (in particular, is the exponential growth rate in that window). The parameters and were fitted via maximum likelihood, assuming that the total number of weekly infections, was Poisson distributed with expectation . Under this model, the log-likelihood of the data (more precisely, of the previously estimated weekly infection counts) is
| (17) |
where refers to iteration over all weeks in the specific sliding window. The maximum-likelihood estimates of and are obtained by solving and which quickly leads to the necessary condition
| (18) |
Eq. (18) was solved numerically by the bisection method to obtain the maximum-likelihood estimate .
To assess estimation uncertainties stemming from sampling stochasticity and uncertainties in the infection risk ratios, the above estimations were repeated 100 times with use of alternative infection risk ratios (for each age group drawn randomly from the set of infection risk ratios previously fitted to various countries) and with replacement of the reported weekly death counts with values drawn from a Poisson distribution with mean . Hence, rather than point estimates, all predictions are reported in the form of medians and equal-tailed confidence intervals. Tables of all estimates for all countries considered up until June 25, 2021, are provided in Supplemental Files 1–5; a visual report is provided as Supplemental File 6.
Assessing the robustness of COVerAGE-DB-based calibrations
To examine whether the age harmonizations of COVerAGE-DB death counts had a major impact on the calibrated infection risk ratios (), the calibrations were also repeated with an independent dataset of national age-stratified death counts obtained from the French INED at https://dc-covid.site.ined.fr/en/data/pooled-datafiles (accessed July 20, 2021). Only countries also included in the calibrations described above and meeting the same data size and quality criteria were considered (the United States and Ukraine). Age groups not intersecting with at least one finite age interval in the INED database were also omitted from the comparison. Supplemental Fig. S9 shows the COVerAGE-DB-based and INED-based calibrated infection risk ratios across all countries and age groups considered; as can be seen, the two sets largely agree (), suggesting that COVerAGE-DB’s age harmonizations did not substantially compromise the model calibrations.
Vaccination data
Data on nationwide completed vaccinations per country over time were obtained from the GitHub repository of the Johns Hopkins Centers for Civic Impact at https://github.com/govex/COVID-19/blob/master/data_tables/vaccine_data/global_data/time_series_covid19_vaccine_global.csv (accessed July 20, 2021). Cumulative vaccination counts were monotonized and interpolated onto a weekly time grid as described above for the death count data.
Declarations
Ethics approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Availability of data and materials
All data used in this article are publicly available at the locations described in the “Methods” section. SARS-CoV-2 prevalences over time, as predicted in this study, are available in Supplemental Files 1–5. A comprehensive visual report for all 165 countries is provided as Supplemental File 6.
Competing interests
The author declares that he has no competing interests.
Funding
The author was supported by a US National Science Foundation RAPID grant.
Author’s contributions
The entire manuscript was prepared by the author.
Acknowledgments
Not applicable.
Footnotes
Supplementary data associated with this article can be found, in the online version, at doi:10.1016/j.ijid.2021.08.067.
Appendix A. Supplementary materials
References
- Alharbi N.K., Alghnam S., Algaissi A., Albalawi H., Alenazi M.W., Albargawi A.M. Nationwide seroprevalence of SARS-cov-2 in saudi arabia. J Infect Public Health. 2021;14:832–838. doi: 10.1016/j.jiph.2021.04.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anand S., Montez-Rath M., Han J., Bozeman J., Kerschmann R., Beyer P. Prevalence of SARS-cov-2 antibodies in a large nationwide sample of patients on dialysis in the USA: a cross-sectional study. Lancet. 2020;396:1335–1344. doi: 10.1016/S0140-6736(20)32009-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Azofeifa A., Valencia D., Rodriguez C.J., Cruz M., Hayes D., Montañez Báez E. Estimating and characterizing COVID-19 deaths, puerto rico, march–july 2020. Public Health Rep. 2021;136:354–360. doi: 10.1177/0033354921991521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baccini M., Cereda G., Viscardi C. The first wave of the SARS-cov-2 epidemic in tuscany (italy): a SI2r2d compartmental model with uncertainty evaluation. PLoS ONE. 2021;16:e0250029. doi: 10.1371/journal.pone.0250029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bastos S.B., Morato M.M., Cajueiro D.O., Normey-Rico J.E. The COVID-19 (SARS-cov-2) uncertainty tripod in brazil: assessments on model-based predictions with large under-reporting. Alex Eng J. 2021;60:4363–4380. [Google Scholar]
- Beaney T., Clarke J.M., Jain V., Golestaneh A.K., Lyons G., Salman D. Excess mortality: the gold standard in measuring the impact of COVID-19 worldwide? J R Soc Med. 2020;113:329–334. doi: 10.1177/0141076820956802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bermingham C.R., Morgan J., Ayoubkhani D., Glickman M., Islam N., Sheikh A. Estimating the effectiveness of first dose of COVID-19 vaccine against mortality in england: a quasi-experimental study. medRxiv. 2021 doi: 10.1101/2021.07.12.21260385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bogogiannidou Z., Vontas A., Dadouli K., Kyritsi M.A., Soteriades S., Nikoulis D.J. Repeated leftover serosurvey of SARS-cov-2 igg antibodies, greece, march and april 2020. Eurosurveillance. 2020;25:2001369. doi: 10.2807/1560-7917.ES.2020.25.31.2001369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bohk-Ewald C., Dudel C., Myrskylä M. A demographic scaling model for estimating the total number of COVID-19 infections. Int J Epidemiol. 2020;49:1963–1971. doi: 10.1093/ije/dyaa198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bolotin S., Tran V., Osman S., Brown K.A., Buchan S.A., Joh E. SARS-cov-2 seroprevalence survey estimates are affected by anti-nucleocapsid antibody decline. J Infect Dis. 2021;223:1334–1338. doi: 10.1093/infdis/jiaa796. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calzetta L., Ritondo B.L., Coppola A., Matera M.G., Di Daniele N., Rogliani P. Factors influencing the efficacy of COVID-19 vaccines: a quantitative synthesis of phase III trials. Vaccines. 2021;9:341. doi: 10.3390/vaccines9040341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chatterjee P. Is india missing COVID-19 deaths? Lancet. 2020;396:657. doi: 10.1016/S0140-6736(20)31857-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chow C.C., Chang J.C., Gerkin R.C., Vattikuti S. Global prediction of unreported SARS-cov2 infection from observed COVID-19 cases. medRxiv. 2020 doi: 10.1101/2020.04.29.20083485. [DOI] [Google Scholar]
- Ciminelli G., Garcia-Mandicó S. Covid-19 in italy: an analysis of death registry data. J Public Health. 2020;42:723–730. doi: 10.1093/pubmed/fdaa165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DESA U.. World population prospects 2019 revision, online edition. Technical report; United Nations, Department of Economic and Social Affairs, Population Division; 2019. Https://population.un.org/wpp/.
- Dowd J.B., Andriano L., Brazel D.M., Rotondi V., Block P., Ding X. Demographic science aids in understanding the spread and fatality rates of COVID-19. Proc Natl Acad Sci U S A. 2020;117:9696–9698. doi: 10.1073/pnas.2004911117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Espenhain L., Tribler S., Jørgensen C.S., Holm Hansen C., Wolff Sönksen U., Ethelberg S. Prevalence of SARS-cov-2 antibodies in denmark 2020: results from nationwide, population-based sero-epidemiological surveys. medRxiv. 2021 doi: 10.1101/2021.04.07.21254703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feyissa G.T., Tolu L.B., Ezeh A. Covid-19 death reporting inconsistencies and working lessons for low- and middle-income countries: opinion. Front Med. 2021;8:150. doi: 10.3389/fmed.2021.595787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flacco M.E., Soldato G., Acuti Martellucci C., Carota R., Di Luzio R., Caponetti A. Interim estimates of COVID-19 vaccine effectiveness in a mass vaccination setting: data from an italian province. Vaccines. 2021;9:628. doi: 10.3390/vaccines9060628. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flaxman S., Mishra S., Gandy A., Unwin H.J.T., Mellan T.A., Coupland H. Estimating the effects of non-pharmaceutical interventions on COVID-19 in europe. Nature. 2020;584:257–261. doi: 10.1038/s41586-020-2405-7. [DOI] [PubMed] [Google Scholar]
- França E.B., Ishitani L.H., Teixeira R.A., DMXd A., Corrêa P.R.L., Marinho F. Deaths due to COVID-19 in brazil: how many are there and which are being identified? Rev Bras Epidemiol. 2020;23:E200053. doi: 10.1590/1980-549720200053. [DOI] [PubMed] [Google Scholar]
- Galvêas D., Barros F., Fuzo C.A. A forensic analysis of SARS-cov-2 cases and COVID-19 mortality misreporting in the brazilian population. Public Health. 2021;196:114–116. doi: 10.1016/j.puhe.2021.05.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haas E.J., Angulo F.J., McLaughlin J.M., Anis E., Singer S.R., Khan F. Impact and effectiveness of mRNA BNT162b2 vaccine against SARS-cov-2 infections and COVID-19 cases, hospitalisations, and deaths following a nationwide vaccination campaign in israel: an observational study using national surveillance data. Lancet. 2021;397:1819–1829. doi: 10.1016/S0140-6736(21)00947-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hallal P., Hartwig F., Horta B., Victora G.D., Silveira M., Struchiner C. Remarkable variability in SARS-cov-2 antibodies across brazilian regions: nationwide serological household survey in 27 states. medRxiv. 2020 doi: 10.1101/2020.05.30.20117531. [DOI] [Google Scholar]
- Kilani A. An interpretation of reported COVID-19 cases in post-soviet states. J Public Health. 2021;43:e409–e410. doi: 10.1093/pubmed/fdab091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kisa S., Kisa A. Under-reporting of COVID-19 cases in turkey. Int J Health Plann Manage. 2020;35:1009–1013. doi: 10.1002/hpm.3031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kobak D. Excess mortality reveals COVID’s true toll in russia. Significance. 2021;18:16–19. doi: 10.1111/1740-9713.01486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- La Marca A., Capuzzo M., Paglia T., Roli L., Trenti T., Nelson S.M. Testing for SARS-cov-2 (COVID-19): a systematic review and clinical guide to molecular and serological in-vitro diagnostic assays. Reprod Biomed Online. 2020;41:483–499. doi: 10.1016/j.rbmo.2020.06.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lachmann A., Jagodnik K.M., Giorgi F.M., Ray F. Correcting under-reported COVID-19 case numbers: estimating the true scale of the pandemic. medRxiv. 2020 doi: 10.1101/2020.03.14.20036178. [DOI] [Google Scholar]
- Larremore D.B., Fosdick B.K., Bubar K.M., Zhang S., Kissler S.M., Metcalf C.J.E. Estimating SARS-cov-2 seroprevalence and epidemiological parameters with uncertainty from serological surveys. eLife. 2021;10:e64206. doi: 10.7554/eLife.64206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lau H., Khosrawipour T., Kocbach P., Ichii H., Bania J., Khosrawipour V. Evaluating the massive underreporting and undertesting of COVID-19 cases in multiple global epicenters. Pulmonology. 2021;27:110–115. doi: 10.1016/j.pulmoe.2020.05.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Le Vu S., Jones G., Anna F., Rose T., Richard J.B., Bernard-Stoecklin S. Prevalence of SARS-cov-2 antibodies in france: results from nationwide serological surveillance. Nat Commun. 2021;12:3025. doi: 10.1038/s41467-021-23233-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leon D.A., Shkolnikov V.M., Smeeth L., Magnus P., Pechholdová M., Jarvis C.I. COVID-19: a need for real-time monitoring of weekly excess deaths. Lancet. 2020;395:e81. doi: 10.1016/S0140-6736(20)30933-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levin A.T., Hanage W.P., Owusu-Boaitey N., Cochran K.B., Walsh S.P., Meyerowitz-Katz G.. Assessing the age specificity of infection fatality rates for COVID-19: meta-analysis & public policy implications. 2020. Working paper 27597. National Bureau of Economic Research. [DOI] [PMC free article] [PubMed]
- Linden M., Dehning J., Mohr S.B., Mohring J., Meyer-Hermann M., Pigeot I. The foreshadow of a second wave: an analysis of current COVID-19 fatalities in germany. arXiv. 2020 [Google Scholar]; Https://arxiv.org/abs/2010.05850
- Linton N.M., Kobayashi T., Yang Y., Hayashi K., Akhmetzhanov A.R., Sm J. Incubation period and other epidemiological characteristics of 2019 novel coronavirus infections with right truncation: a statistical analysis of publicly available case data. J Clin Med. 2020;9:538. doi: 10.3390/jcm9020538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lipsitch M., Donnelly C.A., Fraser C., Blake I.M., Cori A., Dorigatti I. Potential biases in estimating absolute and relative case-fatality risks during outbreaks. PLoS Negl Trop Dis. 2015;9:e0003846. doi: 10.1371/journal.pntd.0003846. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lloyd-Sherlock P., Sempe L., McKee M., Guntupalli A. Problems of data availability and quality for COVID-19 and older people in low- and middle-income countries. Gerontologist. 2021;61:141–144. doi: 10.1093/geront/gnaa153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Long Q.X., Tang X.J., Shi Q.L., Li Q., Deng H.J., Yuan J. Clinical and immunological assessment of asymptomatic SARS-cov-2 infections. Nat Med. 2020;26:1200–1204. doi: 10.1038/s41591-020-0965-6. [DOI] [PubMed] [Google Scholar]
- Louca S., Astor Y.M., Doebeli M., Taylor G.T., Scranton M.I. Microbial metabolite fluxes in a model marine anoxic ecosystem. Geobiology. 2019;17:628–642. doi: 10.1111/gbi.12357. [DOI] [PubMed] [Google Scholar]
- Lu F.S., Nguyen A.T., Link N.B., Davis J.T., Chinazzi M., Xiong X. Estimating the cumulative incidence of COVID-19 in the united states using four complementary approaches. medRxiv. 2020 doi: 10.1101/2020.04.18.20070821. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Madden F.N., Godfrey K.R., Chappell M.J., Hovorka R., Bates R.A. A comparison of six deconvolution techniques. J Pharmacokinet Biopharm. 1996;24:283–299. doi: 10.1007/BF02353672. [DOI] [PubMed] [Google Scholar]
- Maugeri A., Barchitta M., Battiato S., Agodi A. Estimation of unreported novel coronavirus (SARS-cov-2) infections from reported deaths: A susceptible–exposed–infectious–recovered–dead model. J Clin Med. 2020;9:1350. doi: 10.3390/jcm9051350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maugeri A., Barchitta M., Battiato S., Agodi A. Modeling the novel coronavirus (SARS-cov-2) outbreak in sicily, italy. Int J Environ Res Public Health. 2020;17:4964. doi: 10.3390/ijerph17144964. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mendel J.M. Springer; New York: 1990. Maximum-likelihood deconvolution. [Google Scholar]
- Merkely B., Szabó A.J., Kosztin A., Berényi E., Sebestyén A., C L. Novel coronavirus epidemic in the hungarian population, a cross-sectional nationwide survey to support the exit policy in hungary. GeroScience. 2020;42:1063–1074. doi: 10.1007/s11357-020-00226-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moore E.H. On the reciprocal of the general algebraic matrix. Bull Am Math Soc. 1920;26:394–395. [Google Scholar]
- Murhekar M., Bhatnagar T., Selvaraju S., Rade K., Saravanakumar V., Vivian Thangaraj J. Prevalence of SARS-cov-2 infection in india: Findings from the national serosurvey, may-june 2020. Indian J Med Res. 2020;152:48–60. doi: 10.4103/ijmr.IJMR_3290_20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murhekar M.V., Bhatnagar T., Selvaraju S., Saravanakumar V., Thangaraj J.W.V., Shah N. SARS-cov-2 antibody seroprevalence in india, august–september, 2020: findings from the second nationwide household serosurvey. Lancet Glob Health. 2021;9:e257–e266. doi: 10.1016/S2214-109X(20)30544-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nah E.H., Cho S., Park H., Hwang I., Cho H.I. Nationwide seroprevalence of antibodies to SARS-cov-2 in asymptomatic population in south korea: a cross-sectional study. BMJ Open. 2021;11:e049837. doi: 10.1136/bmjopen-2021-049837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Natashekara K. COVID-19 cases in india and kerala: a benford’s law analysis. J Public Health. 2021 doi: 10.1093/pubmed/fdab199. [DOI] [PMC free article] [PubMed] [Google Scholar]; Fdab199
- Nguimkeu P., Tadadjeu S. Why is the number of COVID-19 cases lower than expected in sub-saharan africa? a cross-sectional analysis of the role of demographic and geographic factors. World Dev. 2021;138:105251. doi: 10.1016/j.worlddev.2020.105251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Driscoll M., Ribeiro Dos Santos G., Wang L., Cummings D.A.T., Azman A.S., Paireau J. Age-specific mortality and immunity patterns of SARS-cov-2. Nature. 2021;590:140–145. doi: 10.1038/s41586-020-2918-0. [DOI] [PubMed] [Google Scholar]
- Ohia C., Bakarey A.S., Ahmad T. Covid-19 and nigeria: putting the realities in context. Int J Infect Dis. 2020;95:279–281. doi: 10.1016/j.ijid.2020.04.062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pastor-Barriuso R., Pérez-Gómez B., Hernán M.A., Pérez-Olmeda M., Yotti R., Oteo-Iglesias J. Infection fatality risk for SARS-cov-2 in community dwelling population of spain: nationwide seroepidemiological study. BMJ. 2020;371:m4509. doi: 10.1136/bmj.m4509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pearce N., Vandenbroucke J.P., VanderWeele T.J., Greenland S. Accurate statistics on COVID-19 are essential for policy guidance and decisions. Am J Public Health. 2020;110:949–951. doi: 10.2105/AJPH.2020.305708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Penrose R. A generalized inverse for matrices. Proc Camb Philos Soc. 1955;51:406–413. [Google Scholar]
- Poljak M., Oštrbenk Valenčak A., Štrumbelj E., Maver Vodičar P., Vehovar V., Resman Rus K. Seroprevalence of severe acute respiratory syndrome coronavirus 2 in slovenia: results of two rounds of a nationwide population study on a probability-based sample, challenges and lessons learned. Clin Microbiol Infect. 2021;27 doi: 10.1016/j.cmi.2021.03.009. [DOI] [PMC free article] [PubMed] [Google Scholar]; 1039.e1–1039.e7
- Pollán M., Pérez-Gómez B., Pastor-Barriuso R., Oteo J., Hernán M.A., Pérez-Olmeda M. Prevalence of SARS-cov-2 in spain (ENE-COVID): a nationwide, population-based seroepidemiological study. Lancet. 2020;396:535–544. doi: 10.1016/S0140-6736(20)31483-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reicher S., Ratzon R., Ben-Sahar S., Hermoni-Alon S., Mossinson D., Shenhar Y. Nationwide seroprevalence of antibodies against SARS-cov-2 in israel. Eur J Epidemiol. 2021;36:727–734. doi: 10.1007/s10654-021-00749-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riffe T., Acosta E., team t.C.D. Data resource profile: COVerAGE-DB: a global demographic database of COVID-19 cases and deaths. Int J Epidemiol. 2021;50 [Google Scholar]; 390–390f
- Rinaldi G., Paradisi M. An empirical estimate of the infection fatality rate of COVID-19 from the first italian outbreak. medRxiv. 2020 doi: 10.1101/2020.04.18.20070912. [DOI] [Google Scholar]
- Salje H., Tran Kiem C., Lefrancq N., Courtejoie N., Bosetti P., Paireau J. Estimating the burden of SARS-cov-2 in france. Science. 2020;369:208–211. doi: 10.1126/science.abc3517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sánchez-Romero M., di Lego V., Prskawetz A., L. Queiroz B. An indirect method to monitor the fraction of people ever infected with COVID-19: an application to the united states. PLoS ONE. 2021;16:e0245845. doi: 10.1371/journal.pone.0245845. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singh B. International comparisons of COVID-19 deaths in the presence of comorbidities require uniform mortality coding guidelines. Int J Epidemiol. 2021;50:373–377. doi: 10.1093/ije/dyaa276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Snoeck C.J., Vaillant M., Abdelrahman T., Satagopam V.P., Turner J.D., Beaumont K. Prevalence of SARS-cov-2 infection in the luxembourgish population: the CON-VINCE study. medRxiv. 2020 doi: 10.1101/2020.05.11.20092916. [DOI] [Google Scholar]
- Soiza R.L., Scicluna C., Thomson E.C. Efficacy and safety of COVID-19 vaccines in older people. Age Ageing. 2021;50:279–283. doi: 10.1093/ageing/afaa274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vahidy F.S., Pischel L., Tano M.E., Pan A.P., Boom M.L., Sostman H.D. Real world effectiveness of COVID-19 mRNA vaccines against hospitalizations and deaths in the united states. medRxiv. 2021 doi: 10.1101/2021.04.21.21255873. [DOI] [Google Scholar]
- Veiga e Silva L., de Andrade Abi Harb M.D.P., Teixeira Barbosa dos Santos A.M., de Mattos Teixeira C.A., Macedo Gomes V.H., Silva Cardoso E.H. Covid-19 mortality underreporting in brazil: Analysis of data from government internet portals. J Med Internet Res. 2020;22:e21413. doi: 10.2196/21413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Verotta D. Two constrained deconvolution methods using spline functions. J Pharmacokinet Biopharm. 1993;21:609–636. doi: 10.1007/BF01059117. [DOI] [PubMed] [Google Scholar]
- Ward H., Atchison C.J., Whitaker M., Ainslie K.E.C., Elliott J., Okell L.C. Antibody prevalence for SARS-cov-2 in england following first peak of the pandemic: REACT2 study in 100,000 adults. medRxiv. 2020 [Google Scholar]; 10.1101/2020.08.12.20173690
- Wiener N. Ãnterpolation, and smoothing of stationary time series. MIT Press; Cambridge: 1964. Extrapolation. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All data used in this article are publicly available at the locations described in the “Methods” section. SARS-CoV-2 prevalences over time, as predicted in this study, are available in Supplemental Files 1–5. A comprehensive visual report for all 165 countries is provided as Supplemental File 6.