Numerical Biomechanics Models of the Interaction Between a Novel Transcatheter Mitral Valve Device and the Subvalvular Apparatus

Abstract

Objective

Mitral valve regurgitation (MR) is a common valvular heart disease where improper closing causes leakage. Currently, no transcatheter mitral valve device is commercially available. Raanani (co-author) and colleagues have previously proposed a unique rotational implantation, ensuring anchoring by metallic arms that pull the chordae tendineae. This technique is now being implemented in a novel device design. The aim of this study is to quantify the rotational implantation effect on the mitral annulus kinematics and on the stresses in the chordae and papillary muscles.

Methods

Finite element analysis of the rotational step of the implantation in a whole heart model is employed to compare 5 arm designs with varying diameters (25.9 mm to 32.4 mm) and rotation angles (up to 140°). The arm rotation that grabs the chordae was modeled when the valve was in systolic configuration.

Results

An increase in the rotation angle results in reduced mitral annulus perimeters. Larger rotation angles led to higher chordae stresses with the 29.8 mm experiencing the maximum stresses. The calculated chordae stresses suggest that arm diameter should be <27.8 mm and the rotation angle <120°.

Conclusions

The upper limit of this diameter range is preferred in order to reduce the stresses in the papillary muscles while grabbing more chords. The findings of this study can help improving the design and performance of this unique device and procedural technique.

Central Message.

Raanani (co-author) and colleagues previously proposed a unique rotational implantation technique for transcatheter mitral valve device to ensure anchoring by grabbing the chordae tendineae. This study aimed to quantify the rotational implantation effect on the mechanical stresses in the chordae and papillary muscles by finite element analysis.

Introduction

Mitral valve regurgitation (MR) is one of the 2 most common valvular heart diseases.¹ Regurgitation is caused by either a mitral valve prolapse (primary MR) or a left ventricular (LV) dysfunction (functional MR). Available treatments include surgical repair or replacement, and percutaneous repair.² While untreated MR leads to considerable morbidity and mortality, the majority of severe MR patients are not surgically treated.^3,4

Transcatheter mitral valve replacement (TMVR) is a potential alternative to surgery for currently untreatable pathologies.⁵ However, there is limited clinical experience with such devices due to the unique challenges that MR imposes.³ Currently, transcatheter heart valve (THV) implantation in the mitral position is mostly done with devices designed for the aortic valve, but this use is restricted mainly for implantations inside a degenerated bioprosthetic valve. For native MR treatment, there is still no FDA approved TMVR device. The only CE-marked approved device, Tendyne (Abbott Laboratories, Chicago, IL, USA), is designed for transapical implantation and not for a transfemoral approach because its anchorage is based on apical tethering. However, there is a significant effort to develop transfemoral TMVR devices.^6,7 The main challenge is to provide anchorage without LV outflow tract obstruction (LVOTO).⁸ Another concern is that the complex and dynamic morphology, together with the high-pressure gradients, may lead to significant paravalvular leakage.⁹ Raanani et al.^10,11 (co-author of this study) invented a unique implantation technique for the positioning and anchoring of a dedicatedly designed TMVR device. The technique is based on a rotational motion that brings the native valve closer to the device. The stent of the device has externally mounted metallic arms that pull the native chords, and consecutively the leaflets of the valve, during this rotation. A possible device design and implantation technique are demonstrated in an animation video by Innovalve Bio Medical Ltd. (Sheba Medical Center, Ramat Gan, Israel).¹² This approach can provide paravalvular sealing by the folded native leaflets while retaining a round design, without the need for a mitral annulus anchorage. This technique is also expected to prevent LVOTO by pulling the anterior leaflet away from the aortic valve. Additionally, this device is designed to treat any type of MR and is expected to allow transfemoral delivery. Although this device is currently under development and the potential of its prototype was already demonstrated in preclinical studies,¹³ the exact design and procedural guidelines still require a better understanding of the cardiac biomechanics and its interaction with the device.

The complicated biomechanics highlight the potential benefit of numerical modeling, enabling virtual experimentations that cannot be performed otherwise. These benefits motivated the development of models of the mitral valve.^14-18 Treatment of MR, both by annuloplasty^19-24 and edge-to-edge procedures,^25-27 have been previously modeled using finite element analysis (FEA). Still, the only models of TMVR were of blood flow post implantation²⁸ or implantation of aortic THV in stenotic mitral valve.²⁹

The aim of this study is to determine how the rotational step of the implantation and the diameter of the device impact the native chordae tendineae, leaflets and papillary muscle. For this purpose, a novel numerical model that includes the chordae tendineae interaction with the device was developed. The ultimate goal is to improve the design of the prosthesis and the procedural technique.

Methods

The mechanical response of the mitral valve, chordae tendineae and left ventricular papillary muscle to the implantation procedure was calculated using FEA. In this study we focus on the unique stage of the suggested deployment process, the rotation of metallic arms that pull the native chordae.¹³ Understanding the biomechanics of this stage is crucial for the evaluation of the technique’s viability. Numerical models of the whole heart, rather than just the mitral valve and its subvalvular apparatus, were employed in this comparative-parametric study. Whole heart models allowed us to avoid fixing the valve and papillary muscles, as usually done in bench test and traditional numerical models, and therefore, not limiting the rotation and tension in the chordae tendineae.

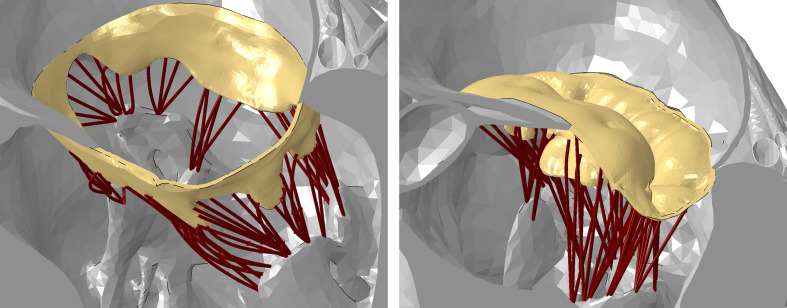
The native heart was modeled using the latest version of the Living Heart Human Model (LHHM, SIMULIA, Dassault Systèmes, Providence, RI, USA).^30,31 The LHHM simulates the entire heart including the electrophysiology and the fibrous architecture of the myocardium. Fluid chambers represent the response of the arterial, venous, and pulmonary systems. The mechanical behavior of the model was previously validated against clinical data to ensure physiological and realistic responses,³¹ specifically for the mitral valve (Fig. 1).^32,33 The mitral valve model includes 30 anterior and 32 posterior chordae. The material properties are based on published measurements^34,35 and calibrated for this model.³³ In a full valve opening state (diastole), the mitral annular dimensions are 32.5 mm and 38.8 mm, for the septal-to-lateral (SL) distance for the intercommissural (IC) distance, respectively. The systolic dimensions are 20.8 mm and 45.8 mm for the SL and IC distances, respectively. The mesh includes 448,298 mechanical elements in total, out of which 70,210 elements are in the mitral valve, 916 in the mitral chordae tendineae, and 59,369 in the papillary muscles. The LHHM model was solved in Abaqus/Explicit (SIMULIA, Dassault Systèmes). In the current study, the arms were rotated during systole while the valve was closed, and the chords were adjacent to the device (see Appendix for further details).

Fig. 1.

Representative views of the mitral valve (yellow), its subvalvular apparatus (brown), and the papillary muscle in the Living Heart Human Model at the end of diastole (open valve, left) and peak systole (closed valve, right). The valve and subvalvular apparatus are fully visible while the chambers are sectioned.

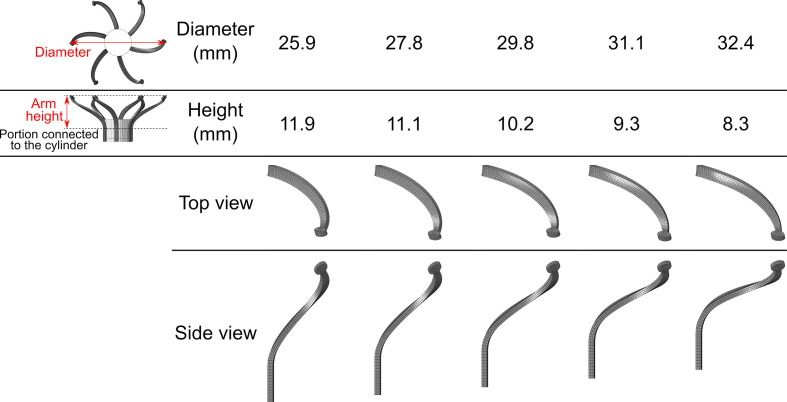
The proposed device includes a bioprosthetic valve mounted on a nickel-titanium alloy (NiTi) stent. The stent has several externally mounted self-expandable arms. In the third stage of the implantation,¹³ which is the focus of the current study, only these arms are expanded, and the stent is kept inside the delivery system. When the delivery system is rotated, the arms grab and pull the chords. Thus, this rotation enables the anchorage of the device and folding of the native valve. In the final implantation step, the entire device is expanded, the native leaflets are clamped between the arms and the stent, preventing unwinding of the device and disabling the native leaflet function. This final step is not modeled in the current study because we focused on the biomechanics of the rotation step only. This simplification allows exploring how the generic arm designs affect the native tissue while isolating this effect from other possible design considerations. Rotation angles of up to 140° and 5 arm designs are considered in this study (Fig. 2). The native heart is free to move during arm rotation, allowing the pulling of the papillary muscles and the mitral annulus. Since the opening of the arms (second step)¹³ is not modeled, the fully expanded arms were placed between the native chords. Moreover, because the arms of the device are designed to stay at a reasonable distance from the left ventricular myocardium, the contact between the arms and the ventricular was not accounted for.

Fig. 2.

Representative views of the 5 designs of the arms with varying diameters and heights.

To generic arm was first created in a configuration representing laser cut tubes, which was expanded to the desired diameter range (25.9 to 32.4 mm) by FEA. Figure 2 shows the 5 resulted arm designs with varying shapes but with similar length and strength. Superelastic NiTi alloy material properties were assigned to the arms.³⁶ The lower portions of the arms were rotated clockwise with the cylinder by angular velocity boundary condition. This rotation direction was chosen to pull the native anterior leaflet away from the LVOT. Six arms were positioned in a radial manner on the cylinder. The pulling effect was modeled by employing contact algorithms between the fabric covered arms, chordae, and the native mitral valve, assuming a friction coefficient of 0.2.

Results

Influence of Arm Length and Rotation Angle on Mitral Annular Perimeter

To compare the impact of varying arm lengths and rotation angles on the mitral annular perimeter, models with arm diameters of 25.9 mm to 32.4 mm were generated and solved. The deformed valves, chordae, and arms at 140° rotation are shown in Figure 3a. This comparison shows a similar annulus shape in all 5 models. Additionally, all the arm lengths were able to grab and pull most of the chordae. Figure 3b plots the calculated relative annular perimeter for each model as a function of the rotation angle, with increments of 20°. The relative annular perimeter is defined as the ratio between the perimeter at a certain angle and the perimeter at the beginning of the rotation (120.7 mm, Supplemental Figure). The perimeter always decreased when increasing the rotation angle. The calculated perimeter started to slightly differ only after 60°, reaching a 2% difference at 140° (Fig. 3b). The influence of the arm diameter and the rotation angle on the annuli can also be observed from their long and short diameters, a common clinical measure. The IC distance trend (Fig. 3c) is similar to that of the perimeter; a steady reduction of the IC distance with the increasing angle, and only a notable difference with larger angles (>80°). The SL distance (Fig. 3d) reaches a plateau at an angle of 80° in most cases. The 29.8 mm and 32.4 mm cases experience a minor increase (+1.7%) and decrease (−2.7%) when reaching 140° compared to their distance at 80°. Table 1 compares the annular perimeter, IC and SL distances at the end of the rotation (140°), demonstrating a similar annular kinematics in the 5 cases.

Fig. 3.

(a) Left ventricular views on the deformed 5 cases of 6 arms with varying diameter after rotation of 140°. The chordae are colored by maximum principal stress magnitudes. (b) Graphs of relative annular perimeter, (c) intercommissural distance, and (d) septal-to-lateral distance as a function of the rotation angle for the 5 cases.

Table 1.

Annular Perimeter, IC, and SL Distances as a Function of Arm Diameter for Rotation Angle of 140°.

Arm diameter, mm	25.9	27.8	29.8	31.1	32.4
Annular perimeter, mm	108.1	108.2	107.1	106.2	106.7
IC distance, mm	39.7	39.9	39.1	39.0	39.2
SL distance, mm	16.7	16.5	16.7	16.2	15.8

Abbreviations: IC, intercommissural; SL, septal-to-lateral.

Chordae Stress as a Function of Arm Diameter and Rotation Angle

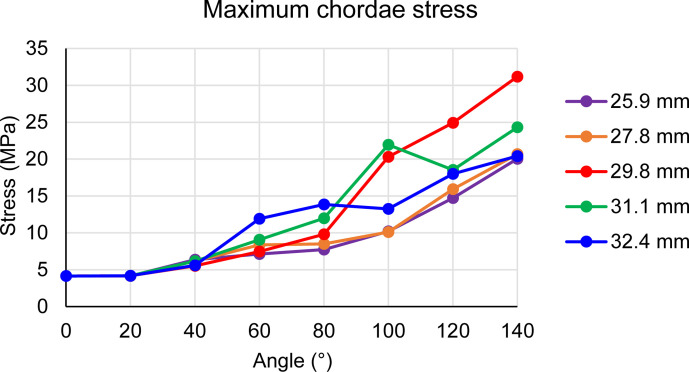
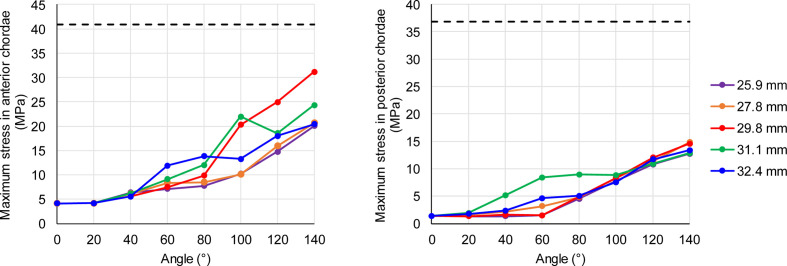
Figure 3a shows the chordae colored by their principal stress magnitudes at a rotation angle of 140°. The highest stresses were found in the 29.8 mm case at 140° and for every rotation angle larger than 113° (Supplemental Video 1). It can also be seen in Figure 4, which plots the maximum stress magnitude in the chordae as a function of the rotation angle. As expected, the stress increases with the angle which increases with time. Similarly, the chordae stresses increase as a function of arm length up to the 29.8 mm diameter, where it starts to decrease. It worth mentioning that a single chord in the 31.1 mm case was pulled by the base of an arm and was exposed to higher stresses than the 29.8 mm case, but it slid off after 100°. None of the cases reached the previously reported mean ultimate tensile stress for mitral chordae.³⁷ Figure 5 presents the maximum stress magnitude in the anterior (left) and posterior (right) chordae, as a function of the rotation angle but can also be seen as a function of time. The mean ultimate strength for each type, as found by Zuo et al.³⁷ for human chordae, are plotted as horizontal dashed lines. In all models, the anterior chordae are closer to the mean ultimate stress than the posterior chordae.

Fig. 4.

Maximum chordae stress as a function of the rotation angle for the 5 cases.

Fig. 5.

Maximum stress in the anterior (left) and posterior (right) chordae as a function of the rotation angle for the 5 cases. Dashed lines represent mean ultimate strength from Zuo et al.³⁷

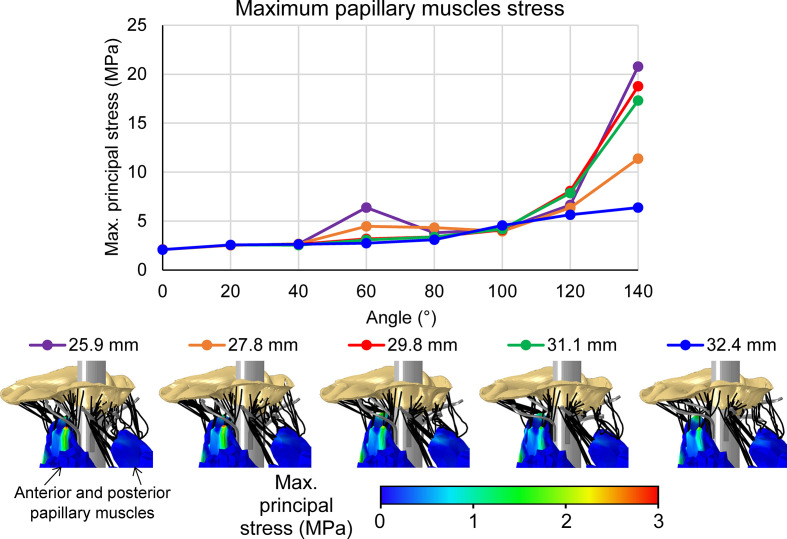
Papillary Muscle Stress as a Function of Arm Diameter and Rotation Angle

Figure 6 compares the maximum principal stress levels in the papillary muscles as a function of the rotation angle and arm length (Supplemental Video 2). The bottom row shows the stress distribution on the outer surface of the papillary muscles, which do not necessarily represent the maximum stress inside the muscles. In general, an increase in the rotation angle leads to higher stresses in the papillary muscles, except for the 2 shortest arms cases where some chordae slid after reaching 60°. There is no clear trend between the papillary stresses and arm length or the calculated stresses in the chordae. In the papillary muscles, the 25.9 mm case experienced the highest stress value (20.8 MPa) while the 32.4 mm had the lowest (6.4 MPa). The stress distribution on the surface demonstrates stress concentration at the tips of the muscles, near the attachment of the chordae. The stress magnitudes in the anterior papillary muscles (Fig. 6, bottom panels) are higher than those found in the posterior muscles. These results correspond to the higher stress magnitudes that were found in the anterior chordae and are due to the fewer posterior chordae in tension (Fig. 6, right chords).

Fig. 6.

Maximum papillary muscle stress as a function of the rotation angle for the 5 cases with representative stress distributions in the papillary muscles at rotation angle of 140°.

Discussion

Raanani (co-author) and colleagues invented a unique technique to position and anchor a TMVR device by pulling the native mitral chordae in a rotational manner.^10,11,13 In this study, numerical biomechanics models were used to simulate the third stage of the device implantation: the rotation of the metallic arms and their interaction with the native valve, subvalvular apparatus, and papillary muscles. The aim of this study was to understand the impact of the device rotation on the annulus kinematics, and the resulting stress, or tension, in the tendineae and papillary muscles. While the ultimate goal is to optimize the prosthesis design and procedural technique, at this stage only 6 generic arms were modeled without the device itself.

Five models with differing arm lengths were compared in varying rotation angles. The traditional simplification of numerical and experimental mitral valve models is to constrain the mitral valve annulus and papillary muscles. However, these locations are exactly the focus of this study, and their response to the device could not be ignored. Therefore, the whole heart was modeled by employing SIMULIA’s LHHM, where the boundary conditions are defined further away from the region of interest. An additional essential capability of the LHHM is the closure of the mitral valve in a contracting heart (see Appendix for further details). Although this was only used to reach the peak systole and to close the valve on the delivery system (Supplemental Figure), it was necessary in order to calculate the changes in the annulus shape and to bring the chordae near the device. It should be emphasized that heart contraction and the annulus motion are calculated and not predefined. Therefore, the delivery system itself altered the closed configuration of the valve.

Reduction of the annular perimeter is an important feature of this novel implantation technique. It enables the use of prosthetic valves with smaller diameters and smaller crimped state, leading to an easier transcatheter delivery. This reduction, together with the folding of the native leaflets during the rotational motion, help sealing paravalvular gaps while having a round valve design. The annular perimeter was analyzed as a function of the rotation angle and compared between the 5 cases (Fig. 3b). All the arm designs resulted in similar kinematics: larger rotation angles reduced the perimeters, and the maximum difference between results was approximately 2% at angle of 140°. For most cases, the SL distance reached a plateau (Fig. 3d) and had a small influence on the perimeter trend, which resembles the trend found for the IC distance (Fig. 3c). A possible explanation for this plateau in the SL distance for angles >80° is that the cylinder of the delivery system, as well as the folded leaflets and the arms around it, prevented a substantial decrease. Since all the cases with the different arm designs had a similar impact on the mitral annulus shape (Table 1), there is no clear preference. Still, smaller diameters are desired due to other kinematic advantages that were not accounted for in the current models, such as the deliverability of the crimped device and that is unwanted that the arms will reach the left ventricular wall.

Another important feature of the proposed implantation technique is that the chordae are grabbed and pulled by the rotating arms. A major consideration for such unprecedented technique is not to injure the native chords. Therefore, the developed stresses in the chordae during the rotation were calculated and compared. The comparison of the maximum stress magnitude in the chordae for each model and as a function of the rotation angle (Fig. 4), shows that the 29.8 mm case experienced the highest stresses for angles bigger than 113°. The observable trends are that the stress increases with the rotation angle and with the diameter up to the 29.8 mm, but then decreases for larger diameters. To compare the stresses with a possible damage or tearing, the chordae were categorized based on their leaflet type and compared with the findings of Zuo et al.³⁷ for the ultimate strength of human chordae tendineae (Fig. 5). While none of the results reached the mean ultimate strength, it should be mentioned that the results of Zuo et al.³⁷ had a large variation. None of the posterior chordae reached the mean minus one standard deviation (mean−1SD) of the ultimate strength reported (14.38 MPa).³⁷ On the other hand, the anterior chordae stress of the 29.8 mm model reached the mean−1SD of the ultimate strength (16.24 MPa)³⁷ at 97°. Additionally, the 2 models with the shortest arms (diameter of 25.9 mm and 27.8 mm) reached this value by the end of the simulation, at angles of 128° and 121°, respectively. Therefore, a possible recommendation based on these results is to use arms with diameters between 25.9 mm and 27.8 mm and to limit the rotation angle to 120°.

Although the stress values in the papillary muscles are less indicative of injury, it is noticeable that the differences only substantial when the angles are larger than 120° (Fig. 6). A comparison of the 2 recommended diameters show that the papillary muscle stress magnitudes are similar in the maximum recommended angle of 120° (6.6 vs 6.3 MPa for the cases of 25.9 mm and 27.8 mm, respectively). When reaching an angle of 140°, the stress magnitude in the 25.9 mm case is larger by 83% than that found in the 27.8 mm case. At this stage (140°), the chordae stresses were similar for these cases (Fig. 4), therefore, the large difference in the papillary muscle stress (Fig. 6) might be attributed to the shorter arms, which can grab fewer chordae. These fewer chords pulled the papillary muscles in a less distributed region, leading to a stress concentration near the chords.

Although computational simulations enable the calculation of essential parameters for the optimization of the unique TMVR implantation technique, there are some potential limitations to it. Firstly, this model is based on a healthy morphology rather than a MR pathology. While it is not an accurate representation of the disease, it allows capturing the annulus perimeter reduction, the most important capability that we tried to test in this study. Following studies will be performed in models with a pathological morphology of various MR types. Validation is lacking due to the limited and simplified in-vitro experiments, whereby the valve fixation prevents a realistic motion of the mitral annulus and the papillary muscles. Our future models will include a more realistic device design based on the conclusions of the current study; these will be validated against dedicated in-vivo animal studies. Still, a parametric study of similar models produces comparable results, and therefore, provides useful information about the identified trends. Worth mentioning that prototypes of the device have already been implanted in-vivo in preclinical studies of acute and chronic efficacy, both in porcine and ovine models,¹³ however, they cannot provide information on the biomechanical effect of the arm length and the rotation angle. Therefore, they cannot be used for validation purposes. The calculated chordae tension data was compared to the failure of human chordae tendineae reported by Zuo et al.³⁷; however, the ultimate strength data provided by Zuo et al. had a large standard deviation and the material properties of our models do not necessarily match them. The reason for this choice is that chordae material properties of the LHHM were dedicatedly calibrated with their section diameter and any change of them will lead to the use of an uncalibrated model. Although Zuo et al.³⁷ also provided Green strain data, this data was not applicable to our models because the anterior chordae reached the Green strain during the systolic closure phase, before the rotation step started. Additionally, our model ignores the contact between the arms and the LV wall because the deployment process was not modeled. Future models will include the entire deployment procedure with a more realistic device design and will account for this contact.

Conclusions

We introduced numerical models of a novel TMVR implantation technique in the native mitral valve of the LHHM. The focus was on the unique rotational implantation and the aim was to find the effect of the unique arm length and rotation angle on the native valve and subvalvular apparatus. Increasing the rotation angle reduced the mitral annulus perimeters and its diameters. Chordae stresses increased with the rotation angle and they were maximized in the 29.8 mm diameter case. Comparison of the chordae stresses with failure criteria range suggest that a smaller diameter range is preferred (<27.8 mm) and that the rotation angle should be limited to 120°. On the other hand, in this diameter range, longer arms would probably be preferred to be able to grab more chords and reduce the stresses in the papillary muscles.