Figure 1.

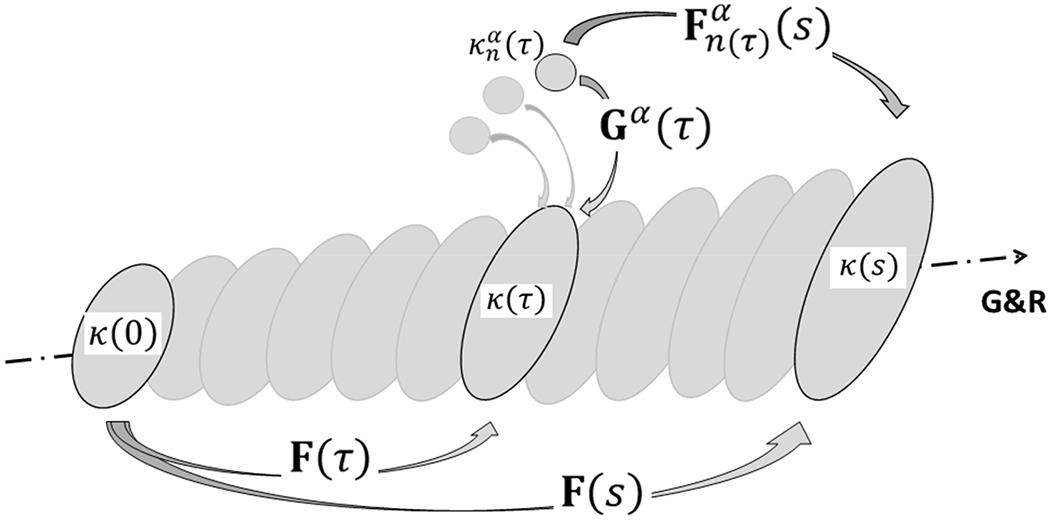
Schema of finite deformations associated with growth and remodeling (G&R) of a soft tissue in maturity using a constrained mixture model. Individual constituents α = 1,2, …, N are assumed to be deposited within extant matrix at preferred deposition stretches G^α(τ) at G&R time τ ∈ [0, s], each relative to individual evolving natural (stress-free) configurations ${\kappa }_n^{\alpha }(\tau )$. Thereafter, these constituents may deform further because they are constrained to move with the tissue, the in vivo configuration of which evolves from κ(τ) at time τ to κ(s) at time s. Note that the reference configuration κ(0) for the tissue need not be stress-free or traction-free; indeed an in vivo configuration such as that near mean arterial pressure is often convenient in vascular mechanics. Finally, it is the constituent-specific deformation ${\mathbf{F}}_{n\left(\tau \right)}^{\alpha }\left(s\right)=\mathbf{F}\left(s\right){\mathbf{F}}^{-1}\left(\tau \right){\mathbf{G}}^{\alpha }\left(\tau \right)$ that is most important because the associated constituent-specific stored energy function depends on this deformation alone. Of course, at the time of deposition, ${\mathbf{F}}_{n\left(\tau \right)}^{\alpha }\left(\tau \right)\equiv {\mathbf{G}}^{\alpha }\left(\tau \right)$.