Figure - PMC

Skip to main content

An official website of the United States government

Here's how you know

Here's how you know

Official websites use .gov
A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS
A lock ( ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

View full-text article in PMC

. 2021 Aug 16;15:705103. doi: 10.3389/fnins.2021.705103

Search in PMC
Search in PubMed
View in NLM Catalog
Add to search

Copyright © 2021 Boschi, Brofiga and Massobrio.

This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.

PMC Copyright notice

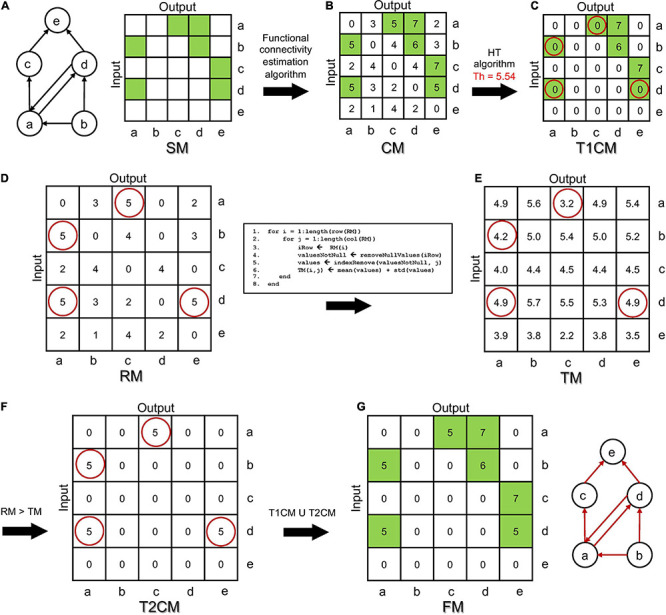
Double Threshold (DDT) algorithm operating principle applied to a simple network. (A) Structural graph made up of n = 5 nodes and the k = 7 structural directed links (left). Structural connectivity matrix (SM) where each green square identifies a structural connection in the graph (right). (B) Functional connectivity matrix (CM) obtained by applying the correlation algorithm to each pair of spike train. In the CM, the green squares show the functional connectivity values that correspond to the actually existing structural links in the network. (C) Applying the first hard threshold (n = 1), the T1CM matrix was computed. In T1CM, the red circles point to those connections incorrectly deleted from the CM (false negatives). (D) The rejected connectivity matrix (RM) is made of all the values that have been previously deleted by applying the hard threshold to the CM. By applying the stripping process summarized in the pseudo-code, (E) the thresholding matrix (TM) resulting from the application of the second step of DDT to the RM is achieved. It contains the threshold for each corresponding value of T1CM. (F) The T2CM shows every RM value that satisfies the condition RM > TM. (G) Final functional thresholded connectivity matrix (FM) and its relative functional graph.