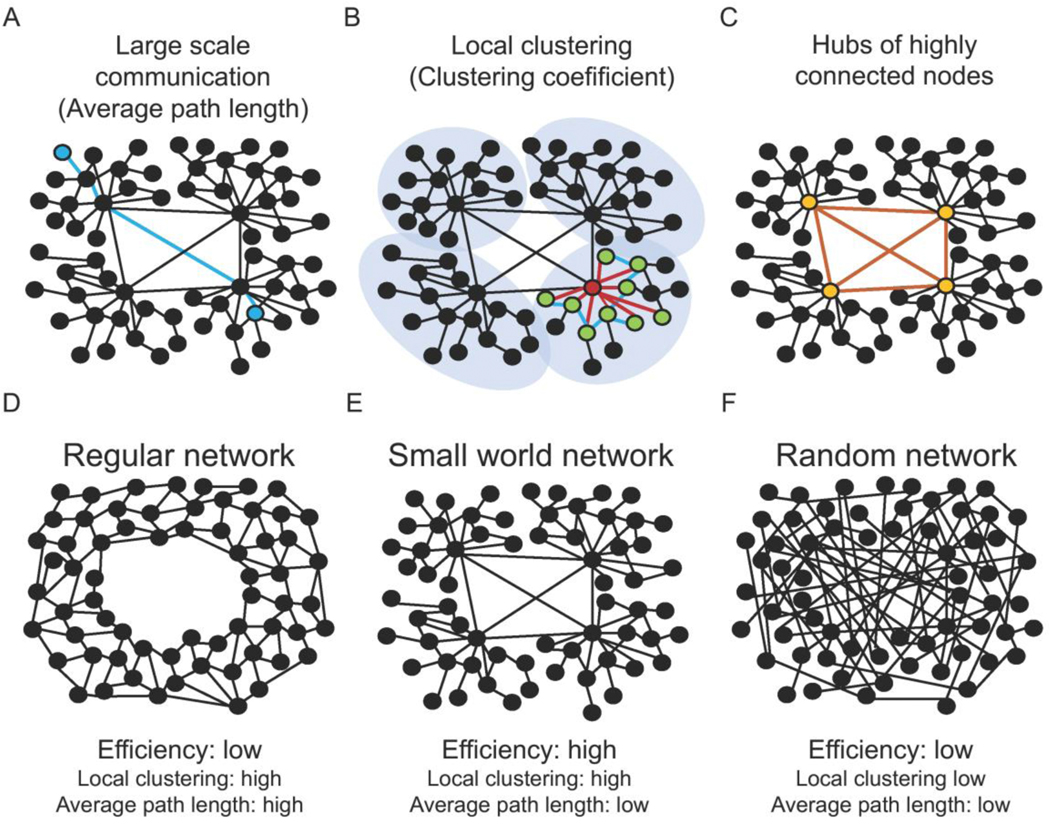
Figure 2.

Graph theoretical characteristics of distributed control networks in the brain. Functional integration capacity in neural networks can be quantified by the average path length (A), which describes the average number of edges (marked in blue) to connect each node to any other node in the network (marked in blue). Functional separation capacity in neural networks can be quantified by the clustering coefficient (B), which describes the interconnectivity of neighboring nodes. The clustering coefficient is exemplified in (B), where connections for one node (marked in red) to its immediate neighbors (marked in green) are colored in red and the connections between these neighbors are marked in blue. All real networks lie on a spectrum between very regularly and very randomly connected. Regular networks (D) exhibit a high clustering coefficient and a high average path length. Random networks (F) show a low clustering coefficient and a low average path length. According to Watts and Strogatz(Watts and Strogatz, 1998), a network shows small-world network properties (E) when it demonstrates a high clustering coefficient as in regular networks and a low average path length as in very random networks. In case a network shows small-world properties, highly connected nodes form hubs that integrate high local connections with long range connections (C).