An Emergent Population Code in Primary Auditory Cortex Supports Selective Attention to Spectral and Temporal Sound Features

Abstract

Textbook descriptions of primary sensory cortex (PSC) revolve around single neurons' representation of low-dimensional sensory features, such as visual object orientation in primary visual cortex (V1), location of somatic touch in primary somatosensory cortex (S1), and sound frequency in primary auditory cortex (A1). Typically, studies of PSC measure neurons' responses along few (one or two) stimulus and/or behavioral dimensions. However, real-world stimuli usually vary along many feature dimensions and behavioral demands change constantly. In order to illuminate how A1 supports flexible perception in rich acoustic environments, we recorded from A1 neurons while rhesus macaques (one male, one female) performed a feature-selective attention task. We presented sounds that varied along spectral and temporal feature dimensions (carrier bandwidth and temporal envelope, respectively). Within a block, subjects attended to one feature of the sound in a selective change detection task. We found that single neurons tend to be high-dimensional, in that they exhibit substantial mixed selectivity for both sound features, as well as task context. We found no overall enhancement of single-neuron coding of the attended feature, as attention could either diminish or enhance this coding. However, a population-level analysis reveals that ensembles of neurons exhibit enhanced encoding of attended sound features, and this population code tracks subjects' performance. Importantly, surrogate neural populations with intact single-neuron tuning but shuffled higher-order correlations among neurons fail to yield attention- related effects observed in the intact data. These results suggest that an emergent population code not measurable at the single-neuron level might constitute the functional unit of sensory representation in PSC.

SIGNIFICANCE STATEMENT The ability to adapt to a dynamic sensory environment promotes a range of important natural behaviors. We recorded from single neurons in monkey primary auditory cortex (A1), while subjects attended to either the spectral or temporal features of complex sounds. Surprisingly, we found no average increase in responsiveness to, or encoding of, the attended feature across single neurons. However, when we pooled the activity of the sampled neurons via targeted dimensionality reduction (TDR), we found enhanced population-level representation of the attended feature and suppression of the distractor feature. This dissociation of the effects of attention at the level of single neurons versus the population highlights the synergistic nature of cortical sound encoding and enriches our understanding of sensory cortical function.

Introduction

Classic accounts of primary sensory cortex (PSC) relegate PSC function to sensory filtering. Accordingly, PSC neurons act as independent filters for low-dimensional sensory features (Hubel and Wiesel, 1968; Merzenich et al., 1975; Kaas et al., 1979) while “association” and prefrontal cortical (PFC) neurons integrate information about behavioral demands and other sensory modalities (Robinson et al., 1978). This account supports a feed-forward nervous system model, where information propagates along distinct processing stages, from peripheral sensory receptors to motor effectors, to enable perception and behavior (Van Essen and Maunsell, 1983; Riesenhuber and Poggio, 1999). Numerous research has shown that PSC neurons form maps of the sensory epithelium, consistent with a role as low dimensional filters (Merzenich et al., 1975). Moreover, secondary and higher-order cortical neurons exhibit diminished, more complex, and task-dependent versions of these maps (Rauschecker and Scott, 2009), and PFC neurons seem to represent all manner of stimulus and cognition-related variables without clear functional topography (Machens et al., 2010).

Primary auditory cortex (A1) receives tonotopic feed-forward input from the lemniscal auditory thalamus and textbooks chiefly describe A1 concerning its role in spectral filtering (Purves, 2004). However, decades of research confound categorization of A1 neurons as static sensory filters: myriad non-sensory variables affect firing rates (FRs), variance and noise correlations in A1 (Osmanski and Wang, 2015; Angeloni and Geffen, 2018; David, 2018). Generally, studies have shown that, under demanding sensory conditions, A1 neuron responses and/or tuning are enhanced, consistent with findings across PSC modalities (Gomez-Ramirez et al., 2016; Mineault et al., 2016; Carlson et al., 2018). Thus, a common view is that A1 and other PSCs are best described as arrays of flexible sensory filters, whereby ongoing behavioral and sensory demands modulate simple feature tuning. However, recent studies show that A1 neurons' synergistic interactions can contribute to sensory processing, a role which often cannot be understood solely based on the activity of individual neurons (Harris et al., 2011; Bathellier et al., 2012; Bagur et al., 2018; See et al., 2018). Rather, individual neurons' activity may be better understood in terms of their contributions within functional ensembles.

We recorded from A1 neurons while monkeys performed a task wherein attention is switched between two different sound features (Fig. 1). We found that A1 neurons robustly represent each task variable: both sound features, as well as task context. Importantly, contrary to findings across sensory modalities showing that attention improves single-neuron encoding, we found no overall attentional modulation of single neurons, since neurons exhibited both enhanced and diminished encoding of the attended feature in equal proportions. The fact that A1 neurons encode each sound feature as well as task context, but display no average attention-related sensory enhancement, suggests that A1 single-neuron activity in this task is not directly related to task performance. These null effects surprised us, since the task presents significant auditory sensory demands related to sound features encoded by A1 neurons. This prompted us to conduct a population-level analysis, inspired by studies performed in PFC (Mante et al., 2013; Rigotti et al., 2013), to make sense of heterogeneous single-neuron representations.

Figure 1.

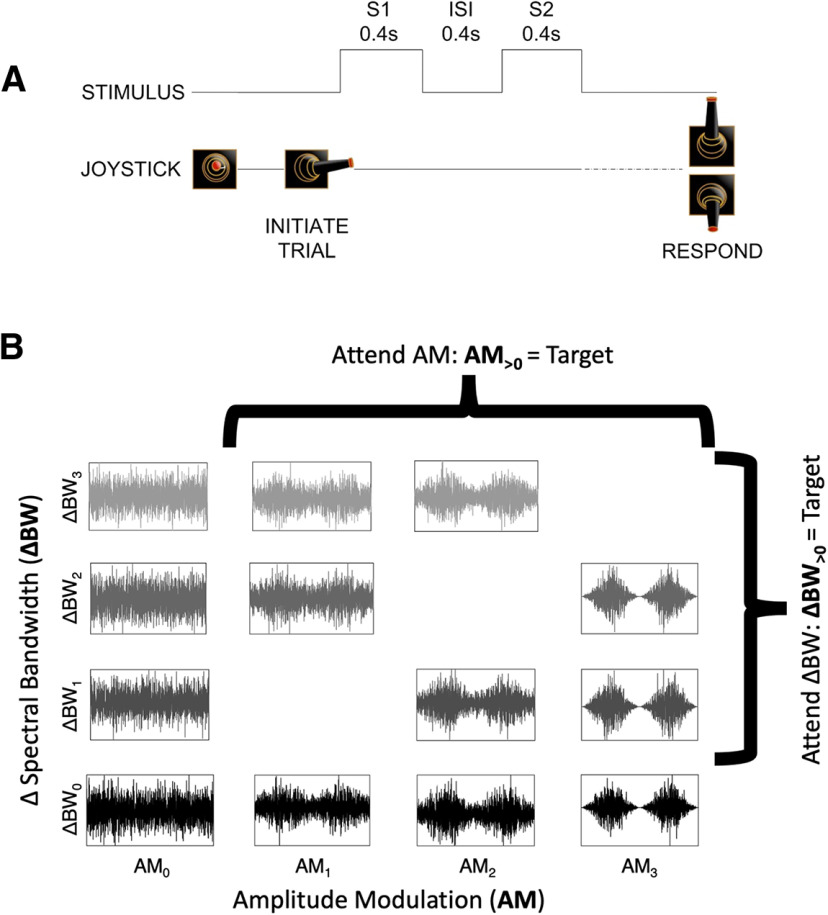
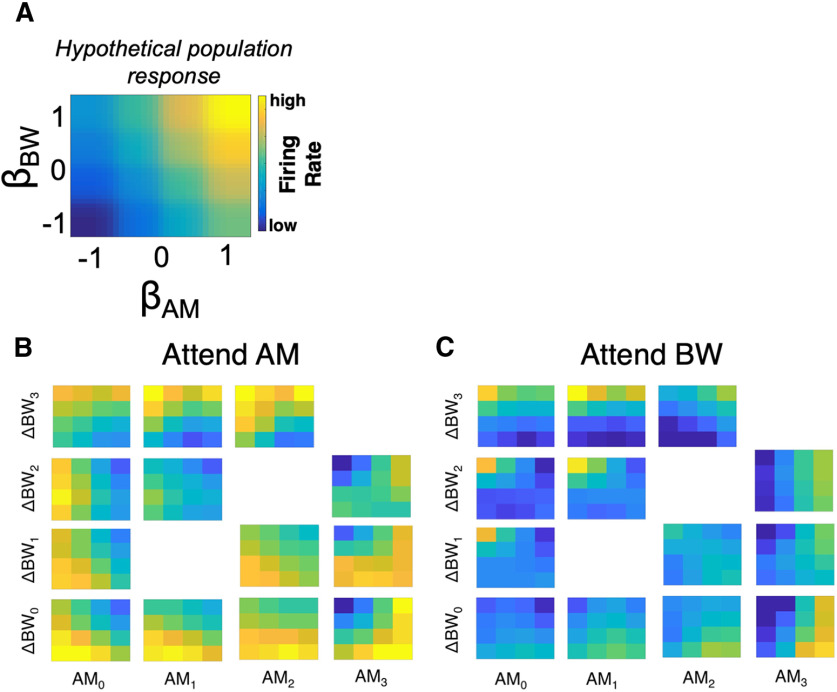
Task and stimulus design. A, Subjects initiated a trial by moving a joystick laterally to present two sequential 0.4-s sounds (S1 and S2) separated by a 0.4-s silent interstimulus interval (ISI). Subjects then used the joystick to make a behavioral report, a “yes” or “no” response indicating whether they detected the attended sound feature in S2. B, Sounds varied along spectral (bandwidth, ΔBW) and temporal (amplitude modulation, AM) feature dimensions. Subjects were trained to selectively attend to changes in one feature dimension or the other across blocks. The S1 sound was always unmodulated and full bandwidth (AM₀–ΔBW₀, bottom left) and the S2 could be any sound in the set. During the attend AM condition all sounds with AM (i.e., with AM₁, AM₂, or AM₃) were targets, and during the attend BW condition all sounds with narrower spectral bandwidth than the standard (ΔBW₁, ΔBW₂, and ΔBW₃) were targets.

Our population analyses focused on reducing the dimensionality of population activity from the number of neurons to the number of variables. Thus, we defined a low-dimensional subspace in which stimulus and behavioral variables are encoded at the population level (Gao et al., 2017). Neural activity projected into this subspace revealed strong effects of attention on population-level sound feature encoding, where the population sensitivity to the attended feature is enhanced. Moreover, variability in these projections accounts for subjects' performance. Further analyses using “surrogate” populations for comparison, in which the single neuron marginal statistics are kept intact while shuffling higher order interactions (Elsayed and Cunningham, 2017), revealed that our findings do not arise as an expected by-product of pooling across many neurons. Rather, these results suggest that sound-encoding in A1 relies on synergies among neurons, and these synergies support the neural code for selective listening.

Materials and Methods

Experimental design

The data presented in this present study have been previously analyzed in a published study (Downer et al., 2017b).

Subjects

We recorded from 92 A1 neurons of two adult rhesus macaques, one female (W, 8 kg) and one male (U, 12 kg). Subjects were each implanted with a head fixation post and a recording cylinder over a left-sided 18 mm parietal craniotomy. Craniotomies were centered over auditory cortex as determined by stereotactic coordinates, allowing for vertical electrode access to the superior temporal plane via parietal cortex (Pfingst and O'Connor, 1980; Saleem and Logothetis, 2012). Surgical procedures were performed under aseptic conditions; all animal procedures met the requirements set forth in the United States Public Health Service Policy on Humane Care and Use of Experimental Animals and were approved by the Institutional Animal Care and Use Committee of the University of California, Davis.

Stimuli

Sound stimuli varied along spectral and temporal dimensions (either or both; Fig. 1B). S1 was always unmodulated, full-bandwidth Gaussian white noise with a nine-octave range (40–20,480 Hz; Fig. 1B, bottom left in stimulus grid: AM₀ΔBW₀). Noise signals were generated from four seeds, which were frozen across recording sessions. The center (log) frequency was 905 Hz and was constant across all stimuli. To introduce spectral and temporal variance, the S1 sound was bandpass filtered to narrow the spectral bandwidth (ΔBW; range: 0.375–1.5 octaves less than the nine-octave full BW) and/or sinusoidally amplitude modulated (AM; range: 28–100% of the depth of the original). Our bandpass filtering method relied on sequential single-frequency addition, thereby reducing envelope variations produced by other filtering procedures (Strickland and Viemeister, 1997). S2 could be any of the stimuli in the set represented in the grid in Figure 1B.

The precise AM and ΔBW values used during recording sessions were tailored to each subject's psychophysical thresholds for detection of each sound feature (AM and ΔBW) in isolation, determined before recordings. The threshold values that we estimated before recordings were used to design the stimulus set to use during recordings; thresholds did not change after recordings began. Three values of each feature were used in recording sessions: one near psychophysical threshold [defined as the modulation level at which the subject's sensitivity, measured using d' (Wickens, 2002) was equal to 1], one slightly above threshold (d' ∼ 1.2), and one well above threshold (d'> 1.5). Experimental values of ΔBW were 0.375, 0.5, and 1 octave for monkey U and 0.5, 0.75, and 1.5 octaves for monkey W. AM depth values were 28%, 40%, and 100% for monkey U and 40%, 60%, and 100% for monkey W.

In analyses in which we collapse data across monkeys, modulation values are presented as ranks relative to subjects' thresholds (AM_0–3 and ΔBW_0–3, where 0 in the subscript reflects no change in that feature dimension relative to the unmodulated, full-bandwidth; Fig. 1B). To reduce the size of the stimulus space, we presented 13 total stimuli during each experimental session, using only a subset of the possible comodulated stimuli (sounds with both AM and ΔBW; Fig. 1B). The AM frequency was held constant in each individual session but varied from day to day. Across sessions we randomly selected the AM frequency from a small range of frequencies (15, 22, 30, 48, and 60 Hz). Previous work has shown that rhesus macaques' average AM detection thresholds are similar across the full range of frequencies used in our task (O'Connor et al., 2011). We chose to randomly select the presented AM frequency to avoid biasing our recordings toward AM-sensitive neurons at the expense of sampling from ΔBW-sensitive neurons.

Sounds were 400 ms in duration with 5-ms cosine ramps at onset and offset. Sounds were presented from a single speaker (RadioShack PA-110 or Optimus Pro-7AV) positioned approximately 1m in front of the subject, centered interaurally. Each stimulus was calibrated to an intensity of 65 dB SPL at the outer ear (A-weighted; Bruel & Kjaer model 2231).

Feature selective attention task

Subjects sat in an acoustically transparent primate chair and used a joystick to perform a “yes-no” task (Fig. 1A). Monkey W used her left hand (ipsilateral to the studied auditory cortex) and Monkey U used his right hand (contralateral to the studied auditory cortex) to manipulate the joystick. LED illumination cued the onset of each trial. Subjects initiated sound presentation with a lateral joystick movement, which was followed by a 100-ms delay and two sequential sounds (S1 then S2) separated by a 400-ms intersound interval (ISI). The trial was aborted if the lateral joystick position was not maintained for the full duration of both stimuli, and an interrupt timeout (5–10 s) was enforced. The first stimulus (S1) was always the unmodulated, full-bandwidth (nine-octave) Gaussian white noise. The second stimulus (S2) was chosen from the set in Figure 1B. S2 sounds were presented pseudorandomly, such that the entire stimulus set across all four noise seeds was represented over each set of 96 trials.

The target feature (ΔBW or AM) alternated by block. Subjects were given an LED cue (green or red, counterbalanced across subjects) for which feature to attend, positioned above the speaker. The cue light remained on throughout the entire block. The first 60–180 trials of each block served as “instruction trials,” containing the S1 and sounds with a single target feature (e.g., for an attend AM block all stimuli in the instruction block were full-bandwidth (ΔBW₀) with AM as the variable (AM_0–3). This allowed the animal to more reliably focus on the attended feature without the distraction of variation in the unattended feature. The length of instruction blocks depended on subjects' performance: if 78% of trials were not correctly performed within 60 trials, another instruction block was begun, up to a limit of three instruction blocks (180 trials); if after three instruction blocks the subject did not reach criterion, the session was terminated. Subsequently an attention block was begun. After the offset of S2, subjects were required to respond with a “yes” joystick movement on trials in which the target feature was present (AM_1–3 during attend AM and ΔBW_1–3 during attend BW; Fig. 1B). “No” responses were made by moving the joystick in the opposite direction. 50% of S2 stimuli contained the target feature, while the remaining 50% did not. The direction to move the joystick for “yes” and “no” responses was counterbalanced between subjects. Subjects were rewarded for hits and correct rejections with water or juice and penalized with a timeout (5–10 s) for false alarms and misses. Incorrect responses were also accompanied by the onset of a white LED light at the same location as the cue lights. The light remained on for the duration of the timeout.

Block length varied from 120 to 360 trials, excluding instruction trials. Length depended in part on subjects' performance: if and only if 78% correct was achieved in two successive 60-trial subblocks could the subject transition to the next attention condition. More than one block per attention condition was performed in a given session. Sessions with fewer than 180 completed trials in either attention condition were excluded from analysis. Subjects' performance in a block was below 78% correct in 14% (5%) of blocks during attend AM (attend BW) conditions. Neural data collected during these relatively low performance blocks was included for further analyses in order ensure sufficient statistical power for analyzing the effects of our many (26) stimulus conditions on neural activity. In a separate set of analyses, we analyzed neural data excluding incorrect trials; we find no qualitative differences in the results regardless of whether incorrect trials were included or excluded.

Single neuron electrophysiology

Recordings were performed in a sound-attenuated, foam-lined booth (Industrial Acoustics Company; 2.9 × 3.2 × 2 m). We independently advanced three quartz-coated tungsten microelectrodes (Thomas Recording, 1- to 2-MΩ resistance, 0.35 mm horizontal spacing) in the vertical plane to the lower bank of the lateral sulcus. Pure tones and experimental stimuli were presented as the animal sat awake in the primate chair during electrode advancement, and neural responses were monitored until the multiunit activity was responsive to sound. We then attempted to isolate single units (SUs). When at least one SU was well isolated on at least one electrode, we measured FR responses to at least 10 repetitions of each of the following stimuli: the unmodulated standard, ΔBW_1–3 as described above, and AM sounds at 100% depth across the full range of frequencies (15, 22, 30, 48, and 60 Hz) as described above. We then cued the subject to begin the task with onset of the cue LED and recorded for the duration of the behavioral task. We repeated measurements of responses to the tested stimuli at the end of the session to ensure electrode stability. Only well isolated SUs stable over at least 120 trials for each attention condition (excluding instruction) were accepted for analysis. SU isolation was determined blind to experimental condition. SUs presented here were well isolated for a mean of 2.6 blocks, with a range of two to five blocks. Removing SUs with only two experimental blocks of isolation (n = 58) from analysis does not qualitatively affect our results nor main conclusions and interpretations.

Extracellular signals were amplified (AM Systems model 1800) and bandpass filtered between 0.3 and 10 kHz (Krohn-Hite 3382), then digitized at a 50 kHz sampling rate (Cambridge Electronic Design model 1401). Contributions of SUs to the signal were determined offline using k-means and principal component analysis-based spike sorting software in Spike2 (CED). The signal-to-noise ratio of extracted spiking activity was at least 5 SDs, and fewer than 0.1% of spiking events assigned to the same SU fell within a 1-ms refractory period window. We also analyzed the spike width of SUs (Hoglen et al., 2018). Consistent with other reports from monkey A1, a low percentage of SUs was classified as “fast-spiking” (12/92; 13.04%).

Recording locations within auditory cortical fields were estimated based on established measures of neural responses to pure-tone and bandpass noise stimuli (Tian et al., 2001; Petkov et al., 2006). SUs' pure-tone frequency tuning was mapped across sessions to determine A1 boundaries based on tonotopic frequency gradients (rostral-caudal axis), width of frequency-response areas (medial-lateral axis), and response latencies. Recorded neurons were assigned to putative cortical fields post hoc. Only SUs assigned to A1 were considered for analysis in this study.

Data analysis

Analyzing subjects' behavior

We analyzed subjects' average performance within each session by calculating a coefficient that quantifies the influence of each feature on subjects' perceptual judgment. The coefficients are derived from the following binomial logistic regression model:

$$\begin{array}{l}P\left(\prime Ye{s}^{\prime }\right)=\frac{1}{1+e^{reg}}\\ reg={\omega }_{AM}\left(A{M}_{VAL}\right)+{\omega }_{BW}\left(B{W}_{VAL}\right)+{\omega }_{AM*BW}\left(A{M}_{VAL}\times B{W}_{VAL}\right)+\alpha \end{array},$$ (1)

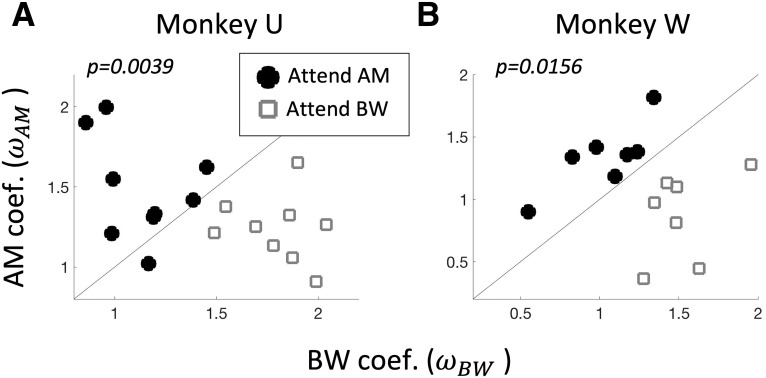
where $A{M}_{VAL}$ and $B{W}_{VAL}$ are the ranked values of AM and ΔBW (0–3), respectively, and $\omega$ are coefficients for the value terms. We include the interaction term (${\omega }_{AM*BW}$), as well as an offset term ($\alpha )$ to capture response bias. Intuitively, as a given feature's influence on the probability of a subject responding “yes” increases, the value of the feature coefficient will increase; when a given feature has no impact on the behavioral response, the value of the coefficient will be ∼0. We calculated each coefficient (${\omega }_{AM}$, ${\omega }_{BW}$, and ${\omega }_{AM*BW}$) within each attention block. We quantified the effect of attention by comparing the distribution of both ${\omega }_{AM}$and ${\omega }_{BW}$ between attention conditions (Fig. 2).

Figure 2.

Both monkeys perform the task. For each monkey (Monkey U in A and Monkey W in B), we show the behavioral coefficients (${\omega }_{AM}$and ${\omega }_{BW}$) calculated from Equation 1 across all sessions in which a recording was performed in A1. Open gray squares and filled black circles indicate the attention condition (attend BW and attend AM, respectively). Selective detection of the attended feature over the distractor feature is evident for both animals by higher ${\omega }_{AM}$ values than ${\omega }_{BW}$ values during attend AM and vice versa during attend BW [signed-rank test, p = 0.0039 (Monkey U), p = 0.0156 (Monkey W)].

Analyzing task and stimulus effects in single neurons

We analyzed the effects of task context, AM and ΔBW on spike counts calculated over the entirety of each 400-ms stimulus. We used a general linear model (GLM) analysis to quantify the influences of each variable [all three main effects (AM, BW, and context) as well as each of the three two-way interactions and the three-way interaction] on each neuron's spike counts. We standardized spike-count ($sc$) distributions across neurons to allow for comparisons between coefficient values by z-scoring spike count distributions across stimuli and task context (i.e., across an entire recording). We also standardized across feature levels (which differ in their absolute values between subjects) by converting each feature value to a rank, between 0 (absence of feature) and 3 (largest feature modulation), then converting ranks to fractions varying between 0 and 1. Context was coded as a binary factor (−1 or 1 for attend BW and attend AM, respectively). The form of the GLM was thus:

$$\begin{array}{l}sc={\beta }_{Ctxt}\left(Ctxt\right)+{\beta }_{AM}\left(A{M}_{VAL}\right)+{\beta }_{BW}\left(B{W}_{VAL}\right)+\\ +{\beta }_{Ctxt\times AM}\left(Ctxt\times A{M}_{VAL}\right)+{\beta }_{Ctxt\times BW}\left(Ctxt\times B{W}_{VAL}\right)+{\beta }_{AM\times BW}\left(A{M}_{VAL}\times B{W}_{VAL}\right)\\ +{\beta }_{AM\times BW\times Ctxt}\left(A{M}_{VAL}\times B{W}_{VAL}\times Ctxt\right)\end{array},$$ (2)

where sc is the standardized trial-by-trial spike count calculated between S2 onset and offset, Ctxt is the context factor, AM_VAL and BW_VAL are the ranked AM and BW levels, respectively, and are coefficients for each factor. In cases where groups of neurons were recorded simultaneously, we calculated the coefficients for each neuron using a unique subset of trials to avoid spurious correlations in the coefficients between neurons. In a separate set of analyses, we analyzed the time course of effects using a 25-ms sliding window, between ISI onset and S2 offset. The window was shifted in 5-ms increments and we analyzed the effects of context, AM and BW and their interactions at each time point.

We also calculated the area under the receiver operating characteristic (ROC area), a $sc$-based measure of sensory sensitivity that corresponds to the ability of an ideal observer to discriminate between two stimuli based on $sc$ alone. Performance ranges from 0.5 (chance) to 1 (for neurons with increasing $sc$ across the range of feature values) or 0 (for neurons with decreasing $sc$ across the range of feature values). ROC area can be interpreted as the probability of an ideal observer properly classifying a stimulus as containing a feature of interest, AM or ΔBW. We calculated ROC area for each stimulus condition. If a neuron's ROC area is 0.5, that is interpreted as a failure to detect the presence of a feature. ROC area was calculated using neural activity between S2 onset and offset only, i.e., during the entire 400-ms S2 presentation.

For each neuron, statistical significance was calculated for each of the coefficients of the GLM by first estimating each coefficients' p value (using the glmfit function in MATLAB), followed by correction for multiple comparisons using the false discovery rate (FDR; Benjamini and Hochberg, 1995). The glmfit function estimates p values based on the estimated coefficient value and the estimated confidence interval thereof, relative to the standard normal distribution. We calculated whether a given coefficient was present among all A1 neurons above chance via a permutation test. For this permutation test we created a null distribution by shuffling the trial-by-trial labels of the variables for each neuron, and then calculating the p value using glmfit and FDR as above. Then, across all 92 neurons, we counted the number of significant coefficients for each variable. We repeated this procedure 100 times to obtain an estimate of the mean and SD of the count of each coefficient spuriously reaching statistical significance. This procedure yielded an estimate that, by chance, 5.02 ± 1.08% of neurons will exhibit a significant coefficient. Therefore, we consider any variable for which we find >6.1% of neurons reaching statistical significance to be reliably encoded by A1 neurons.

Analyzing task and stimulus effects in neural populations

We used a targeted dimensionality reduction (TDR) approach to estimate the low-dimensional subspaces in which task variables may be encoded (Mante et al., 2013), and then quantified the strength of that encoding using the ROC area. TDR is a method of calculating a weighted average of neural activity across a sample of neurons. Weights for each neuron in TDR are first calculated as the linear regression coefficients relating the task variables to neurons' FRs (Eq. 2). Then, the matrix of weights across neurons and variables is orthogonalized to allow us to estimate projections (weighted averages) of neural activity uniquely related to each task variable. TDR both reduces the dimensionality of the population response from # neurons to # projections and provides a way of “de-mixing” neural activity across a population of neurons with mixed selectivity.

TDR, and its conceptual motivation, are illustrated with a toy example in Figure 3. Here, we contrast two hypothetical cases in which feature-selective attention modulates single-neuron tuning via a feature-selective gain (FSG) mechanism (Martinez-Trujillo and Treue, 2004) by simulating two separate populations of 100 sensory neurons responding to stimuli varying along two feature dimensions. FSG is a model of attention whereby the response of a neuron is determined by both its sensory response function and a multiplicative gain parameter that depends on the neuron's preference for the attended feature, yielding larger responses when attention is directed toward the neuron's preferred feature. In the example case of “unmixed selectivity” (Fig. 3A–D), single neurons' tuning strength to either of two features (feature A and feature B) is largely mutually exclusive (i.e., non-zero tuning strength for feature A is associated with ∼0 tuning strength for feature B, and vice versa). Simulated neurons' FRs are thus a function of only one feature and a FSG parameter that multiplicatively scales neurons' FRs according to whether attention is directed toward feature A (Fig. 3A) or feature B (Fig. 3B). In this way, the slope of the “feature tuning strength versus FR” plot increases for the attended feature (e.g., compare the red dots in Fig. 3A,B). This leads to a larger response to a feature when attention is directed toward that feature (Fig. 3C,D).

Figure 3.

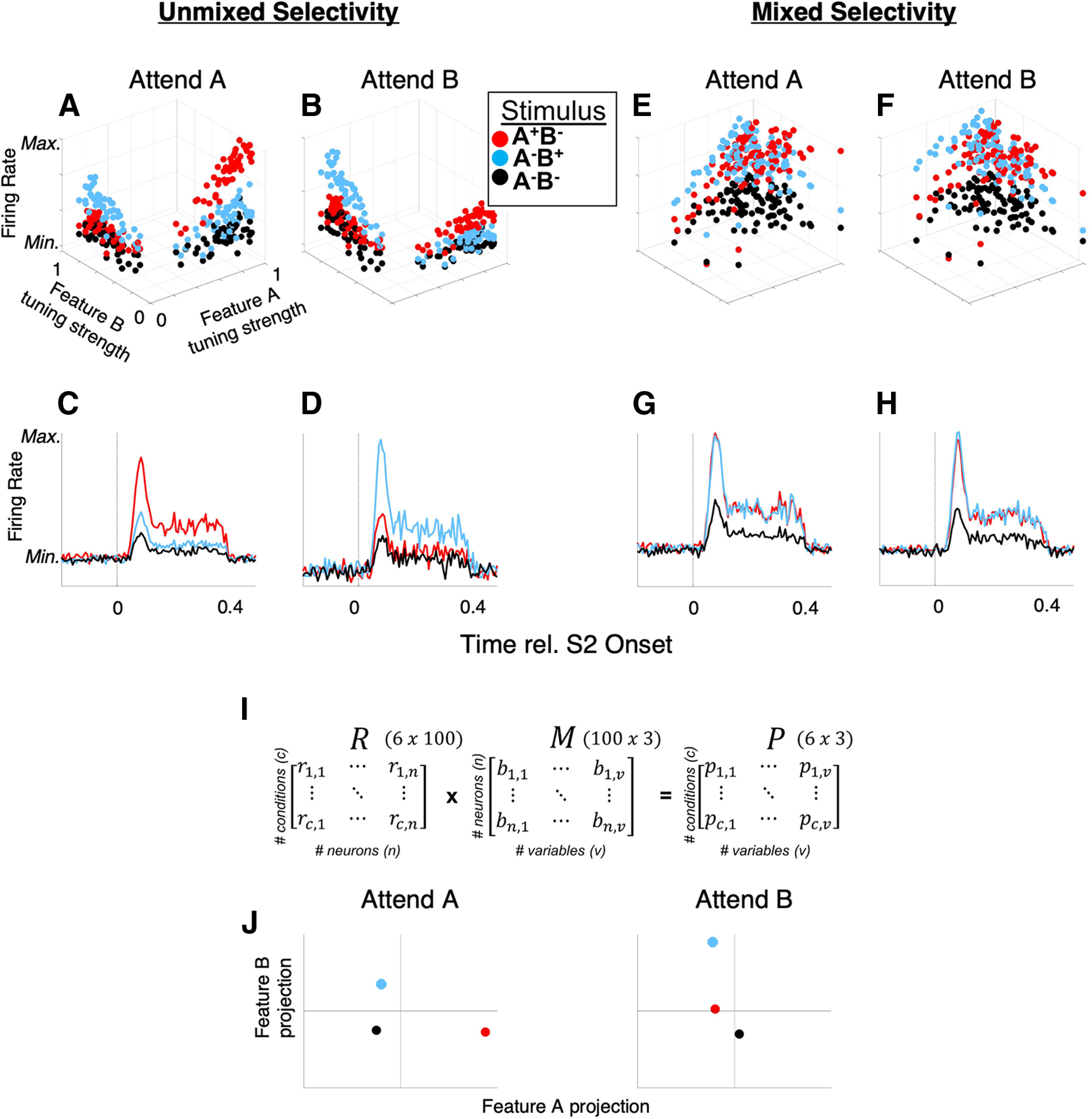
TDR for populations with “mixed selectivity.” Contrasted are two simulated populations of neurons (A–D, unmixed selectivity and E, F, mixed selectivity), each exhibiting the same FSG influence on single neurons' FRs. With unmixed selectivity, FSG results in a simple marginalization of population FR that enhances the response to the attended feature (e.g., FR responses to feature A (stimulus A⁺B^–, red dots and red PSTHs) exceed those of the feature B (A^–B⁺) and null (A^–B^–) stimuli when feature A is attended (A, C), and vice versa when feature B is attended (B, D). E–H, However, when neurons exhibit mixed selectivity for features A and B (i.e., they exhibit significant tuning strength for both features), the same modeled FSG parameter does not yield an attention-related increase in population-averaged FR responses to the attended feature (e.g., responses to A⁺B^– and A^–B⁺ are roughly equal across attention conditions). However, using TDR to de-mix population response outputs (I) can yield population-level responses that reflect a strong enhancement of the representation of the attended versus unattended feature. The matrix M, consisting of orthogonalized regression coefficients (the β_x terms in Eq. 2) for each neuron, transforms the neural data in R to a set of $\nu$-dimensional coordinates (e.g., in our case the 3 feature variables AM, ΔBW, and context), for each experimental condition in matrix P. “Variables” are the dimensions along which the conditions vary; the three variables in this example are the two stimulus features (A, B) and attention. J, A hypothetical TDR-estimated response (in arbitrary units of projection magnitude) for a population similar to that depicted in E–H is illustrated in J for the three stimuli (A^–B^–, A⁺B^–, and A^–B⁺) for each attention condition (attend A and attend B).

However, if neurons' feature tuning exhibits mixed selectivity, i.e., non-zero tuning to both features, the same FSG mechanism fails to meaningfully segregate the population-averaged FRs (Fig. 3E–H). Thus, when single neurons exhibit mixed selectivity in their tuning to different sensory features, FSG as a mechanism of attention exhibits no average attentional enhancement (Fig. 3G,H). However, via TDR, we can find the data transformations that yield “de-mixed” representations of task variables via projections of neural population activity onto task-specific axes. In Figure 3I, we show how a full data matrix, R (of z-scored FRs) can be transformed to a matrix P of uncorrelated projections via multiplication by an orthogonalized regression coefficient matrix, M (see next paragraph for detailed description). Thus, each of the six experimental conditions illustrated here (c = 3 stimulus conditions × 2 attentional; rows of R, and rows of P) yields a unique population response (projection) represented in matrix P. Therefore, each row of P represents the population response as single point in three-dimensional space, where each dimension corresponds to a task variable (ß_A, ß_B, and ß_context, comprising the columns in matrix M and P). This process is analogous to re-weighting each neurons' outputs at the downstream synaptic level. Each axis in Figure 3J thus could represent the activity of a single hypothetical downstream neuron receiving its inputs from a neural population similar to that depicted in Figure 3E–H, the input weights of which are selectively shaped to maximize the unique encoding of each task variable; for clarity, we display two two-dimensional spaces (one for each attention condition) where the dimensions correspond to the variables feature A (x-axis) and feature B (y-axis). Whereas population-averaged single-neuron FRs fail to reveal an effect of FSG, projections onto the stimulus-variable axes may reveal a strong effect of attention: in the attend A space, the population response to the A⁺B^– stimulus (red) projects much farther along the feature A axis than in the attend B space. Likewise, the population response to the A^–B⁺ stimulus (blue) projects farther along the feature B axis during the attend B space than in the attend A space.

To implement TDR, the data are represented in matrix R, which contains one column for each neuron and one row for each condition. Note, in the present study we refer to “conditions” as distinct combinations of AM, ΔBW and context, such that we have 26 total experimental conditions (13 AM × ΔBW combinations across two attention conditions). We refer to “variables” as the three dimensions along which all conditions vary, namely the two sound features (AM, ΔBW) and context (attention). The matrix M consists of the set of regression coefficients calculated for each variable in Equation 2, orthogonalized via orthogonal triangular decomposition (qr command in MATLAB) to obtain the matrix. M is thus a set of uncorrelated variable coefficient vectors that can be used to project our data onto orthogonal axes corresponding to task variables in the form of matrix P. We illustrate the process of TDR on our data in Figure 4. We have uploaded MATLAB code demonstrating the analysis steps for running TDR to https://github.com/joshuaDavidDowner/TDRdemo.

Figure 4.

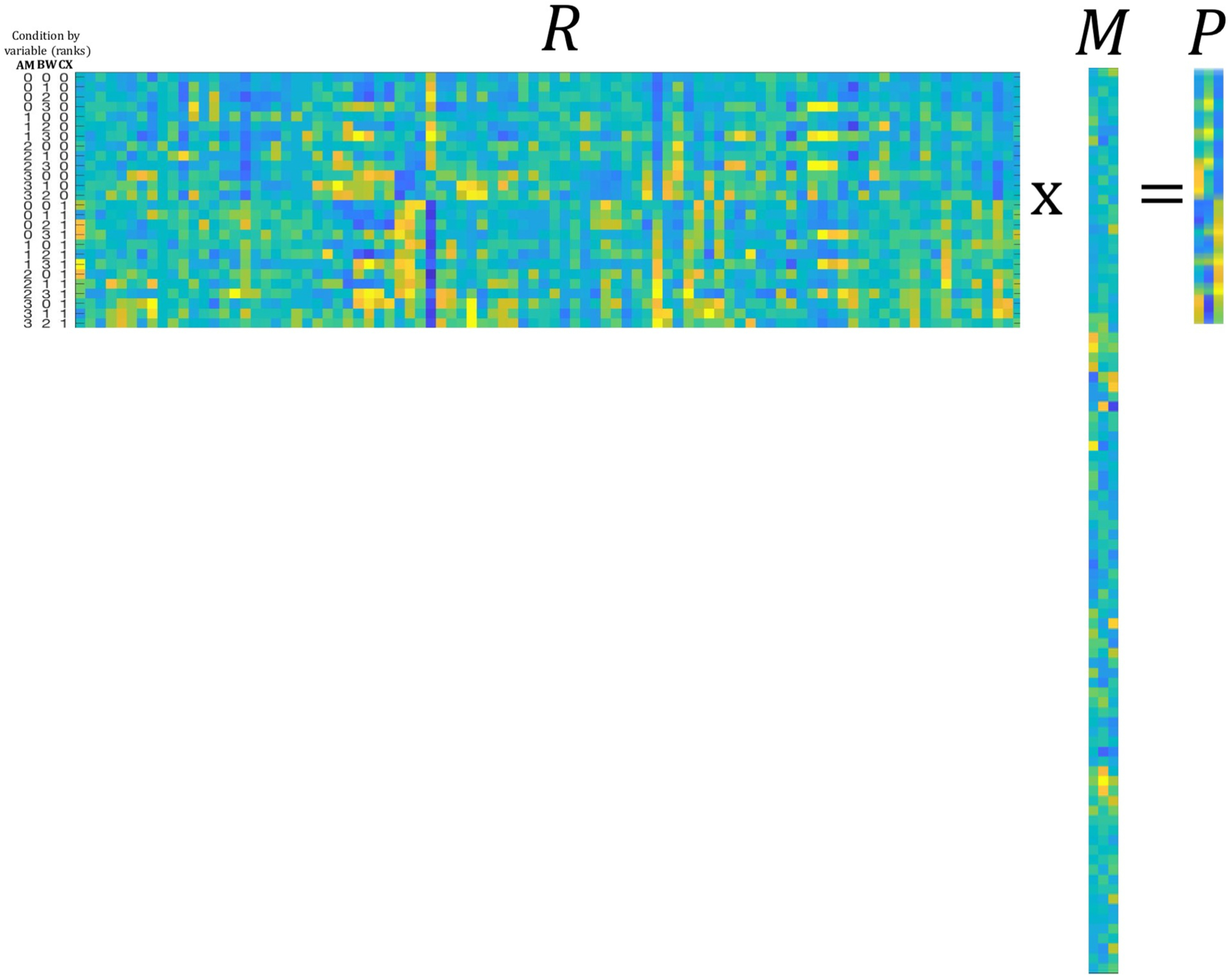
Concrete description of matrices R, M, and P as expressed in our data. Across matrices, the color scheme parula represents the values (FR in R, coefficient value in M, and projection magnitude in P) of the entries in each matrix (maxima: yellow; minima: blue). The matrix R is 26 × 92, where each row corresponds to a condition (all 26 combinations of 4 AM depths, 4 bandwidths, and 2 attend conditions) and each column to a neuron (92 neurons). The matrix M is 92 × 3 where each row corresponds to a neuron and each column to a vector of orthogonalized variable coefficients (β_AM, β_BW, and β_context from Eq. 2). The matrix P is 26 × 3 where each row corresponds to a condition and each column to a variable. Here, the columns of M are (1) AM coefficients; (2) BW coefficients; and (3) context coefficients. Multiplying R × M yields the matrix P in which each row corresponds to one of the 26 conditions and each column to a variable, or axis. Each value of P represents the projection of the population response to a condition along a given axis. For instance, column 1 of P exhibits increasing values as the rank value of AM increases (see condition labels to the left of matrix R). The color bar on the right applies to all matrices and indicates values from minimum (blue) to maximum (yellow) for FR (matrix R), coefficient (matrix M), and projection (matrix P). The variable labels to the left of matrix R correspond to Amplitude Modulation (AM), Bandwidth (BW) and Context (CX).

Simulating neural population activity

We analyzed neural population activity both in small ensembles of simultaneously recorded neurons and by simulating population activity by combining the activity of neurons that were recorded during different sessions. For analyzing simultaneously recorded ensembles, we included ensembles of at least three neurons (n = 12 ensembles). For combining non-simultaneously recorded neurons into simulated populations, we used a bootstrapping approach to estimate the mean and variance of population projections. Namely, we constructed neural populations of size n = 92 neurons by randomly sampling, with replacement, from our set of 92 sampled A1 neurons. We similarly simulated trials by re-sampling (with replacement) from the distribution of spike counts of each neuron in each of the 26 experimental conditions (10 trials per condition). We constructed 100 simulated populations in this way.

An important consideration with this approach is that, by combining neurons across experimental sessions, and by randomly re-sampling trials, we fail to approximate correlated and intrinsic variability between and within neurons, respectively. Therefore, the matrix of simulated spike counts within a condition is transformed to introduce noise correlations and neuron-intrinsic variability that match that observed in the data (Downer et al., 2017b). We determined the desired noise correlation value between a given pair of neurons by measuring the noise correlations between the simultaneously recorded pairs of neurons in the data (n = 434 pairs) and fitting a linear regression to those noise correlation values to determine the impact of AM and ΔBW tuning correlation, joint FR and attention condition on noise correlations. We determined the desired neuron-intrinsic variability by calculating the Fano factor (variance/mean rate) for each neuron and scaling its simulated spike count distribution to match the observed Fano factor. Thus, our simulated populations contained realistically structured spike count variability. The methods for introducing realistic noise correlations and Fano factor in simulated neural populations are detailed by Shadlen and Newsome (1998) and Downer et al. (2017a). All simulated population results presented in this manuscript are from simulations in which we impose noise correlations between pairs of neurons as described above. However, our understanding of the effects of noise correlations on population coding is still incomplete. While it is known that many facets of the population, including heterogeneity among constituent neurons, the presence or absence of “information-limiting correlations,” the relationship between constituent neurons' tuning properties, and many others (Ecker et al., 2011; Hu et al., 2014; Kanitscheider et al., 2015), it is likely that the impact of noise correlations meaningfully differs for different neural populations. Therefore, we also performed the same analyses on simulated populations with both unstructured global noise correlations (i.e., noise correlations were on average 0.06 between pairs of neurons, regardless of tuning correlations, FR, or attention condition) as well as without imposed noise correlations (i.e., noise correlations were on average 0 between the neurons in the population). Results were qualitatively similar regardless of whether and how we imposed noise correlations, although the simulations with unstructured or net zero noise correlations yielded a weaker effect of attention on population-level feature sensitivity than simulations in which we modeled the observed attention-related changes in noise correlations.

We determined the sensitivity for each sound feature in each population (both simultaneously recorded and simulated) by calculating the ROC area (as described for single neurons) by comparing distributions of simulated trial-by-trial projections onto each sound feature axis (as opposed to distributions of trial-by-trial spike count distributions). The projections in a given trial were calculated as in Figure 3I. We calculated decoding accuracy (ROC area) for AM and BW by comparing the distribution of projections of AM_>0 versus AM₀ stimuli and BW_>0 versus BW₀ stimuli, respectively, along each feature's axis. A linear support vector machine (SVM) was fit to a training set and performance evaluated on a test set of withheld data.

We calculated choice-related ROC area for the simulated populations by comparing trial-by-trial projection distributions along each axis for “yes” and “no” behavioral response trials for the same stimulus. We used the same SVM algorithm as described for calculating sound feature sensitivity to discover the linear plane of separation between the three-dimensional (AM × BW × context) projections for “yes” and “no” trials. This analysis was meant to illuminate the relationship between our estimates of population sensory activity and subjects' perceptual report, regardless of the stimulus condition or task context. Importantly, we only analyzed choice-related ROC area for stimuli with roughly equal numbers of “yes” and “no” responses, namely, those stimuli near perceptual threshold, where subjects made at least five correct and incorrect judgements, similar to Niwa et al. (2012a). This provision protects against biases arising from re-sampling from distributions with few values, for which mean and variance estimates are unreliable. In our data, the only stimuli that met this criterion across sessions were the AM₁–ΔBW₀ and AM₀–ΔBW₁ sounds.

In order to evaluate the extent to which findings of simulated population-level activity deviate from expected effects of pooling across groups of neurons, we constructed 1000 surrogate populations with intact single-neuron tuning but decimated higher-order correlations among them (Elsayed and Cunningham, 2017). This method constructs surrogate populations by shuffling the original data labels, but then recovering (to the extent possible) the marginal and covariance features of the original data by transforming the shuffled data using a “readout” matrix. Thus, the final surrogate populations contain modeled neurons that closely approximate the neurons in the original data, but with higher-order correlations abolished. We calculated sensory sensitivity (ROC area) and choice-related activity precisely as we did with the intact data set, across 1000 surrogate populations. These distributions produced by the surrogate populations provide benchmarks for the expected results given effects accountable by single-neuron features without complex interactions among them.

Results

Monkeys successfully perform the feature selective attention task

Within each feature-attention (context) block, we quantified the degree to which a change in each feature influenced subjects' probability of a “yes” response using a binomial logistic regression (see Materials and Methods). We determined significant task performance for each monkey by comparing the distributions of regression coefficients for the attended feature versus the unattended feature using a Wilcoxon signed-rank test. We observed higher ${\omega }_{AM}$ values than ${\omega }_{BW}$ values during the “attend AM” condition, and vice versa during the “attend BW” condition [p = 0.0039 (Monkey U), p = 0.0156 (Monkey W); Fig. 2].

A1 neurons exhibit mixed selectivity for sensory features and task context

We quantified encoding of behavioral (context) and acoustic (AM and BW) variables on the FRs of recorded A1 neurons (n = 92) using multiple linear regression (Equation 2). For each neuron, we calculated a set of coefficients describing the main effect of each of these three variables and all pairwise interactions (seven total coefficients per neuron).

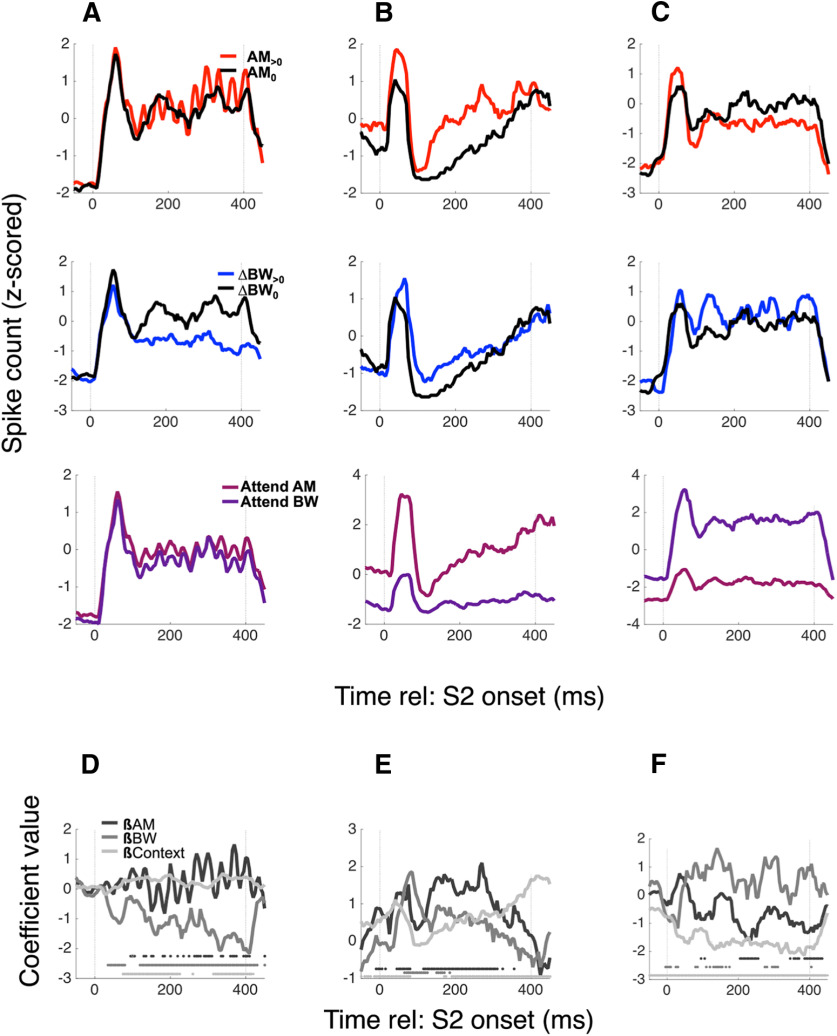
We saw diverse encoding of task variables, as shown in several example neurons (Fig. 5; each column of panels is a different neuron). Figure 5A–C, top row, shows FRs, collapsed across context and BW condition, separated by AM condition (red: AM_>0; black: AM₀ = no AM). The middle row shows FRs separated by BW condition, and the bottom row shows FRs separated by context. The neuron in Figure 5A encodes BW, shown by a decreased FR for BW_>0 conditions relative to BW₀ conditions (β_BW = −1.18, p = 4.57e-29), while the neurons in 5B and 5C encode both sound features as well as context [β_AM = 0.63, p = 5.7e-7; β_BW = 0.31, p = 0.016; β_Ctxt = 0.47, p = 6.2e-14 (Fig. 5B); β_AM = −0.34, p = 0.0012; β_BW = 0.33, p = 0.0033; β_Ctxt = −0.86, p = 2.3e-42 (Fig. 5C)], albeit with different directions of FR changes [e.g., they both encode AM, but 5B exhibits an increased FR for AM (positive β_AM), while 5C exhibits a decreased FR (negative β_AM)]. Figure 5D–F shows the time course of the coefficient values calculated for each variable by the neurons in Figure 5A–C, respectively. Taken together, these three example neurons illustrate that single A1 neurons exhibit diverse encoding of variables relevant for this task, often encoding context as well as both sound features. Although it is unsurprising to find that A1 neurons encode the sensory and context variables in this task, these example neurons provide an example of the apparently “tangled” nature of this coding (Rust and DiCarlo, 2010). Because A1 FRs simultaneously encode multiple independent variables, single-neuron FRs may provide a poor code for any given variable on a trial-by-trial basis, i.e., the unweighted FRs of individual A1 neurons do not unambiguously encode the variables necessary for task performance. Therefore, marginalizing across single neurons by unweighted averaging yields an ambiguous representation. A summary across all single neurons is shown in Figure 6.

Figure 5.

A1 neurons exhibit mixed selectivity for sensory and task variables. Example PSTHs for three neurons are shown in columns A–C, with average FRs collapsed across irrelevant variables to reveal AM (top row), BW (middle), and context (bottom) encoding. The neuron in A exhibits no AM-dependent or context-dependent changes in sustained FR, but decreases its FR when ΔBW > 0. The neuron in B increases its rate for both AM > 0 and ΔBW > 0 (red PSTH and blue PSTH above black PSTH, respectively) and has an overall higher FR during the attend AM context (pink PSTH above purple PSTH). The neuron in C decreases rate for AM > 0, increases rate for ΔBW > 0, and prefers the attend BW condition. We calculated coefficients for each variable over a sliding window (“0” means that variable does not contribute to FR), and these time-varying coefficient trajectories are shown in D–F for the neurons in A–C, respectively. The greyscale markers along the x-axis in the bottom of each panel indicate significance of each coefficient within the 25-ms time bin in which the coefficient was calculated.

Figure 6.

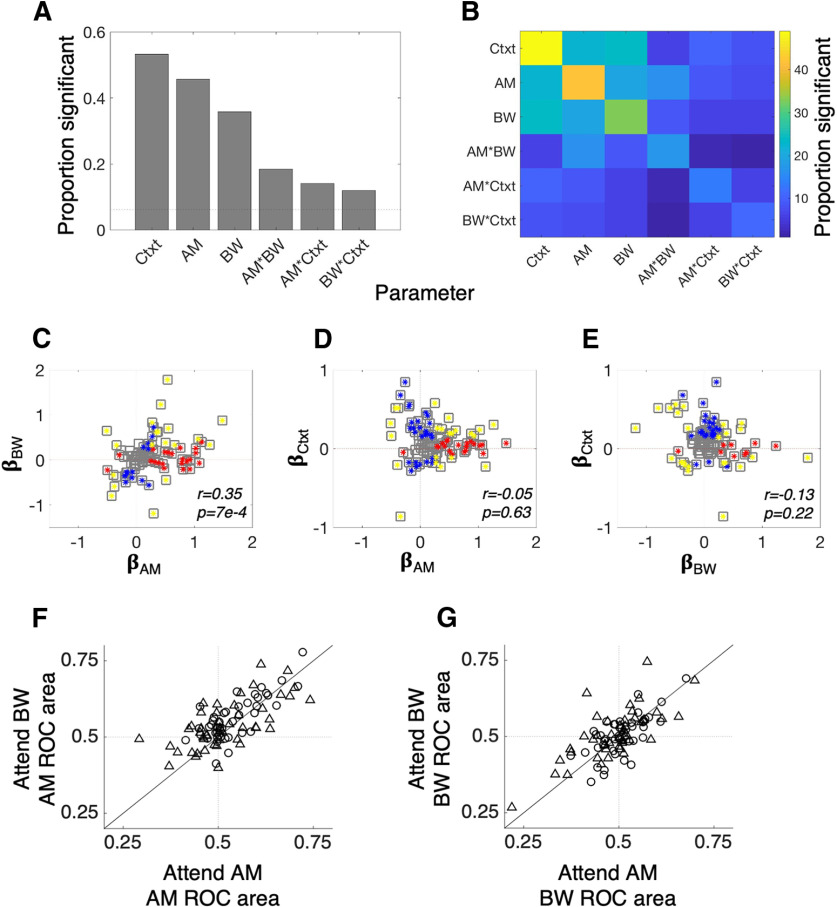
A1 neurons robustly encode context, AM, and BW. A, The histogram showing the proportion of neurons with significant context (Ctxt), AM, and BW coefficients reveals that each variable modulates the FR of many A1 neurons. Importantly, interactions between the variables are relatively rare, suggesting that each variable tends to make an independent, linear contribution to neurons' FRs. The relative paucity of cells with significant context × AM or context × BW interaction terms suggests that sound feature tuning in A1 is relatively constant between attention conditions. B, The heat map illustrates the joint encoding of task variables. Many neurons that encode one variable also encode at least one other. For instance, more than half of those cells that encode context also encode either AM or BW. C, There is a positive relationship between AM and BW encoding, such that the single-neuron FRs tend to fail to disambiguate between AM and BW. D, E, Context exhibits no significant relationship between AM or BW tuning, suggesting that the FSG model is inconsistent with our data. In C–E, red markers indicate a significant coefficient for the variable on the x-axis, blue markers indicate a significant coefficient for the variable on the y-axis and gold markers indicate significance for both variables. F, G, Single-neuron feature sensitivity is consistent across attention conditions. F, Average single-neuron AM sensitivity, as measured with ROC area (AM ROC area) does not change between conditions. G, Same as F but for BW ROC area.

A significant number of A1 neurons encodes each of the variables tested here, i.e., >6.1% of neurons have significant coefficients for each variable (for how we determine this significance cutoff, see Materials and Methods). Context has a significant main effect in more neurons than either acoustic feature, as measured by the proportion of neurons with significant context coefficients (49/92 with significant context coefficients; 42/92 with significant AM coefficients; 33/92 with significant ΔBW coefficients; Fig. 6A). Significant interaction effects were less common (13/92 with significant AM × context coefficients; 11/92 with significant BW × context coefficients), suggesting that attention does not tend to change A1 neurons' feature tuning. This can be seen clearly in Figure 6B as well; the color map of proportions of significant coefficients exhibits a markedly higher proportion of main effects (main diagonal) than interactions. This contrasts with findings from tasks comparing passive listening and active auditory behaviors on A1 tuning: across many studies, active task engagement result in large changes in A1 tuning (David, 2018). These studies have been interpreted as evidence that A1 single-neuron tuning tracks behavioral demands, namely that tuning is enhanced when animals are actively engaged with sounds (Niwa et al., 2012b).

Figure 6C provides a possible reason for the relatively low incidence of attention-related changes in A1 neuron tuning. We plot the value of AM coefficients against the value of BW coefficients and find that a majority of neurons have similar AM and BW tuning as measured by the sign of the coefficient (Spearman's r = 0.35, p = 0.0007). In other words, A1 neurons rarely uniquely encode one sound feature or the other because feature tuning co-varies at the single-neuron level (similar to Fig. 3E–H). This prevents single-neuron tuning from providing a robust basis for attentional perceptual enhancement. We also find no significant correlation between context main effect coefficients and main effects of either sound feature [β_AM vs β_Ctxt, Spearman's r = −0.05 p = 0.63 (Fig. 6D); β_BW vs β_Ctxt, Spearman's r = −0.13 p = 0.22 (Fig. 6E)], nor do we find any significant correlation between any other pairs of coefficients (Spearman's correlation, p > 0.05 for all). A common finding in the attention literature is that feature attention leads to FSG, whereby neurons tuned to the attended feature exhibit an increased FR (Martinez-Trujillo and Treue, 2004). An FSG effect in these data might manifest as a positive relationship between β_AM and β_Ctxt and a negative relationship between β_BW and β_Ctxt (since context is coded as +1 for attend AM and −1 for attend BW in Eq. 2). On the contrary, our analyses reveal no such correlations. Alternatively, an FSG effect in our data may also manifest as a preponderance of cells with positive AM × Ctxt coefficients and/or negative BW × Ctxt coefficients and/or a negative relationship between AM × Ctxt and BW × Ctxt. We found no evidence for any of these alternatives: the median AM × Ctxt coefficient is −0.05 while the median BW × Ctxt coefficient is −0.01 (Wilcoxon signed-rank text, p = 0.99 and p = 0.11, respectively) and there is no significant correlation between AM × Ctxt and BW × Ctxt (Spearman's r = 0.04, p = 0.48). Thus, these analyses reveal no evidence that an FSG mechanism operates on individual A1 neurons to support feature selective attention.

Average A1 neurons' feature sensitivity is constant across attention conditions

In the analyses presented in Figure 6A–E, we calculated coefficients across the entire experiment and used sound feature $\times$ context interaction terms as a measure of attentional modulation of A1 neuron tuning. We next measured the average effects of attention on single-neuron feature decoding accuracy by calculating ROC area for each feature in each attention condition for each neuron (see Materials and Methods). Comparing ROC area for both features across conditions reveals no attentional modulation of single-neuron feature sensitivity (Fig. 6F,G; results shown are collapsed across all AM and BW levels). In Figure 6F, the AM ROC area is shown for the attend AM condition on the x-axis and the attend BW condition on the y-axis. Although we do observe some scatter around the unity line, neurons increase or decrease their AM ROC area with equal likelihood (Wilcoxon signed-rank test, p = 0.74). In Figure 6G, we show the BW ROC areas across attention conditions and, again, find no average effect of attention on this single-neuron metric of feature tuning (Wilcoxon signed-rank test, p = 0.73). Therefore, when comparing feature tuning across the more rigorous demands of different feature attention conditions, we do not observe tuning changes that have been found in several prior studies comparing A1 tuning between passive versus active conditions and between attend-toward versus attend-away conditions (Niwa et al., 2012b; von Trapp et al., 2016; Schwartz and David, 2018).

TDR analysis reveals attentional enhancement of sensory encoding

Given the complexity of the task, we reasoned that a plausible strategy for adaptive feature selection might be a distributed population code. Population codes can allow unambiguous and simultaneous encoding of many variables by distributing the task-relevant signals across single neurons (Fusi et al., 2016). Thus, during population encoding of complex auditory scenes involving multiple relevant variables, single-neuron FRs may provide a complicated snapshot of the overall operations of A1. We therefore modeled A1 population coding by subsampling from our set of single neurons and projected population vector activity (Georgopoulos et al., 1986) onto axes corresponding to AM and BW encoding using TDR (Mante et al., 2013; see Materials and Methods; Figs. 3, 4). Such approaches have been employed in studies of higher-order cortex to disambiguate the often-heterogeneous single neuron signals observed there (Machens et al., 2010; Mante et al., 2013; Rigotti et al., 2013).

We provide a description of population responses across experimental conditions in Figure 7. Here, population-averaged FRs (averaged over the entire 400-ms S2 presentation epoch; Fig. 1A) are displayed in 4 × 4 grids, where each element represents FR averaged over a subgroup of neurons sorted by β_AM (x-axis) and β_BW (y-axis). A hypothetical population response in Figure 7A shows a case in which neurons with positive β_AM and positive β_BW fire above their mean rates, whereas neurons with negative β_AM and β_BW fire below their mean rates. Our data displayed in this manner qualitatively reveal effects of stimulus feature and task context (Fig. 7B,C). Each panel in Figure 7B,C shows the population response (as in Fig. 7A) for a given stimulus combination of AM and ΔBW (for example, the lower right panel in Fig. 7B is the population response in attend-AM to the ΔBW₀–AM₃ stimulus).

Figure 7.

A population-level analysis for feature encoding in A1. A, We provide a schematic illustration of our population-level analysis approach. The grid in A is a hypothetical population response pattern, with population FR organized by β_AM and β_BW. For this hypothetical response, the group of neurons with positive β_AM and β_BW exhibit high FRs. B, In our data, population response patterns differ across the stimulus set (population response grids arranged as the stimulus matrix in Fig. 1B), with clear differences in population responses related to increasing AM and BW levels. C, Moreover, comparing C to B reveals substantial differences in population responses related to attention.

By and large, increases in AM level result in population activity patterns that are increasingly biased toward high spike counts among neurons with positive β_AM and increases in ΔBW level result in patterns with high spike counts among neurons with positive β_BW. Moreover, comparing population activity patterns for a given stimulus across attention conditions hints at complex changes in FR based on both β_AM and β_BW. For instance, for AM₀–ΔBW₂, the population activity pattern during attend AM (Fig. 7B) seems to exhibit high FRs for neurons with negative β_AM, regardless of β_BW. However, during attend BW (Fig. 7C), the population activity exhibits low FRs for all neurons except for those with negative β_AM and positive β_BW. Taken together, these panels provide a visual intuition for how stimuli are encoded in a distributed manner across the A1 population and how attention qualitatively affects this encoding.

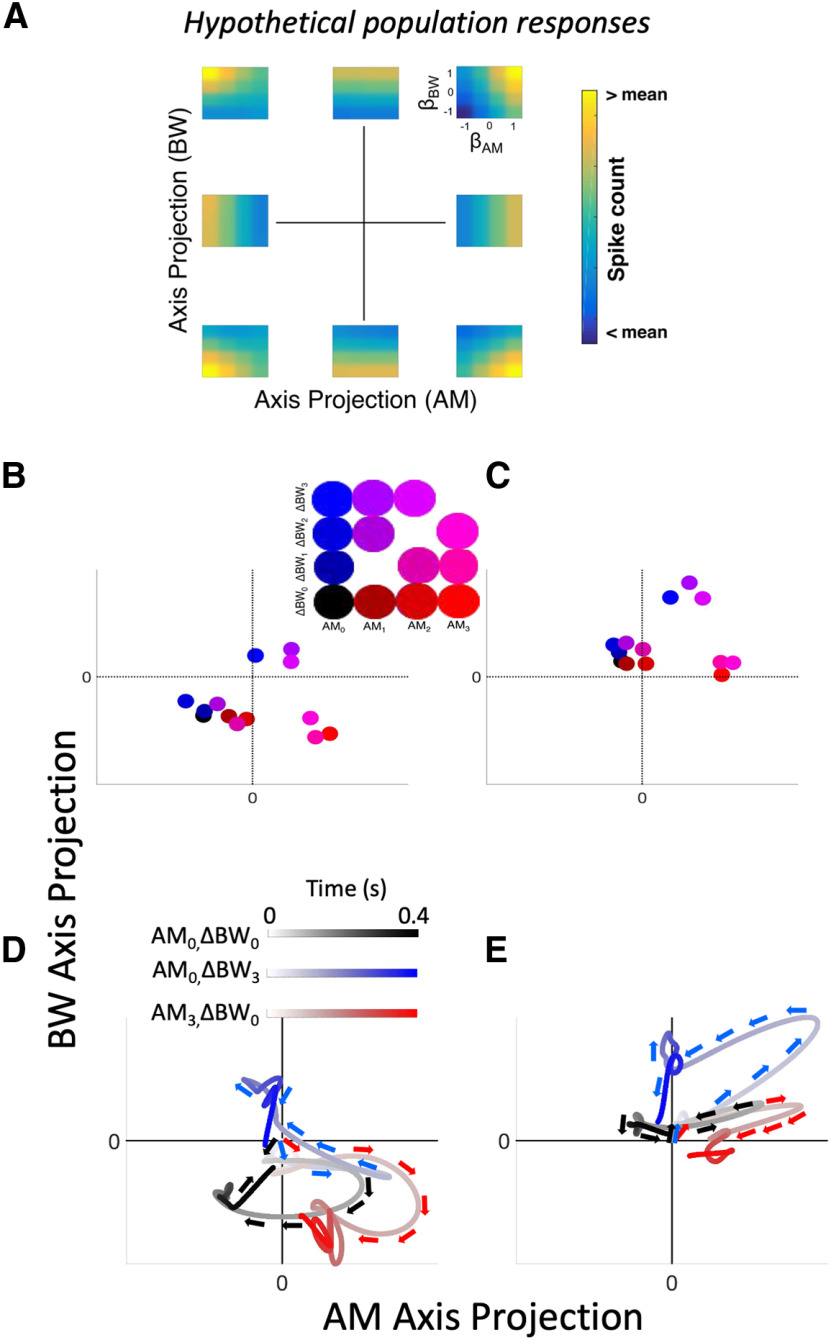
Projecting population activity into a low-dimensional subspace via TDR provides a compact way of quantifying population response patterns (Fig. 8). We focus here on stimulus-related projections. In Figure 8A, eight distinct, idealized population responses show where each population response falls on an AM axis projection versus BW axis projection plot, e.g., the population response in the upper right of Figure 8A, would have a value near 1 for both its AM and BW axes projections, and thus would be a dot in the upper right for panels in Figure 8B–E. In order to project our data onto these coordinates, we constructed pseudo-populations by sampling from our pool of recorded neurons and simulating trial-by-trial population responses, which are projected onto these two-dimensional coordinates via a linear combination between a data matrix of spike counts (R) and a coefficients matrix (M; Fig. 3I,J; Materials and Methods). Projections in the attend AM and attend BW conditions for each stimulus are shown in Figure 8B,C, respectively; projections averaged over simulated trials are shown for each stimulus condition (see inset for color code). By design, increasing AM levels correspond to greater projections along the AM axis than along the BW axis, and increasing ΔBW levels correspond to greater projections along the BW axis than along the AM axis (e.g., AM₃ and ΔBW₃ stimuli project farthest along the AM and BW axes, respectively). The topography of stimulus responses clearly differs between attention conditions. Thus, whereas single-neuron FRs fail to disambiguate between AM and BW, populations comprising these same neurons successfully encode each feature when their outputs are re-weighted using TDR.

Figure 8.

Neural activity projected into sensory-defined subspace reveals sound feature encoding. A, Our approach involves projecting responses of populations of neurons into lower-dimensional condition subspace defined by the stimulus variables (dimensionality reduced from n neurons to p conditions). The eight hypothetical responses in A show idealized population responses that project in corresponding eight points in the AM axis projection versus BW axis projection coordinates. (context dimension not shown.) B, Color-coded stimulus responses (see inset) in the attend AM condition are shown projected into axis-projection subspace. Symbols represent mean responses over simulated trials. Markers representing projections along the AM axis exhibit increasing (red) values, whereas markers representing projections along the BW axis exhibit increasing (blue) values, indicating population-level encoding of sound features. In the upper right quadrant of the inset are purple markers, representing stimuli containing both features, and markers with low color values (including black) are found in the lower left quadrant of the inset. C, Same as B but for the attend BW condition. Axes in B, C are scaled equally. Comparing encoding subspaces across conditions reveals substantial effects of attention on sensory subspace projections. D, Trajectories over time through the sensory subspace for three representative stimuli [AM₀–BW₀ (black), AM₀–BW₃ (blue), AM₃–BW₀ (red)] reveal encoding over the entire course of S2 presentation for the AM attend condition. Trajectories begin at the x and y origin, indicating no sensory evidence for either AM or BW. Directly after stimulus onset, trajectories for each stimulus follow similar paths, then diverge substantially. Trajectories reach a peak of separation, such that AM₀–BW₃ and AM₃–BW₀ projections are in opposite quadrants (upper left and lower right, respectively), both roughly orthogonal to the AM₀–BW₀ projection. Then, during the end of the stimulus response, trajectories approach the origin. E, Same as in D but for the attend BW condition. Trajectories in both conditions exhibit an early, non-selective course wherein each stimulus projects to roughly the same area within the subspace. During the middle of the stimulus, trajectories reach their maximum separation, then trend back toward the origin. These trajectories suggest that feature selection during sound perception evolves over time, beginning with a general detection phase, followed by a discrimination phase, then returning to a non-encoding area of the subspace thereafter. Note that the window size and shift increment here (25 and 5 ms, respectively) in D, E are the same used in Figure 5D–F.

Moreover, we observe that trajectories through this subspace exhibit interesting temporal dynamics (Fig. 8D,E). For clarity, only three stimulus response trajectories are shown [AM₀ΔBW₀ (black), AM₃ΔBW₀ (red), and AM₀ΔBW₃ (blue)]. Time is shown with lighter shading of the lines early in the stimulus gradually getting darker over time. The initial excursion for each stimulus, corresponding to the onset response immediately after time 0, appears initially ambiguous and gradually differentiates over the course of a S2 presentation. Projection trajectories appear maximally separate roughly in the middle of the stimulus, and by the end of the stimulus presentation, trajectories return to the origin of the subspace. These temporal dynamics suggest that early population responses function to detect a rapid change, regardless of feature, whereas sustained responses elicit finer-grained feature selectivity. Differences between onset and sustained responding have been widely observed in auditory cortex (Wang et al., 2005; Kuśmierek et al., 2012; Osman et al., 2018). These findings support that the temporal dynamics of sensory neuron responses correspond to distinct encoding stages in population activity patterns.

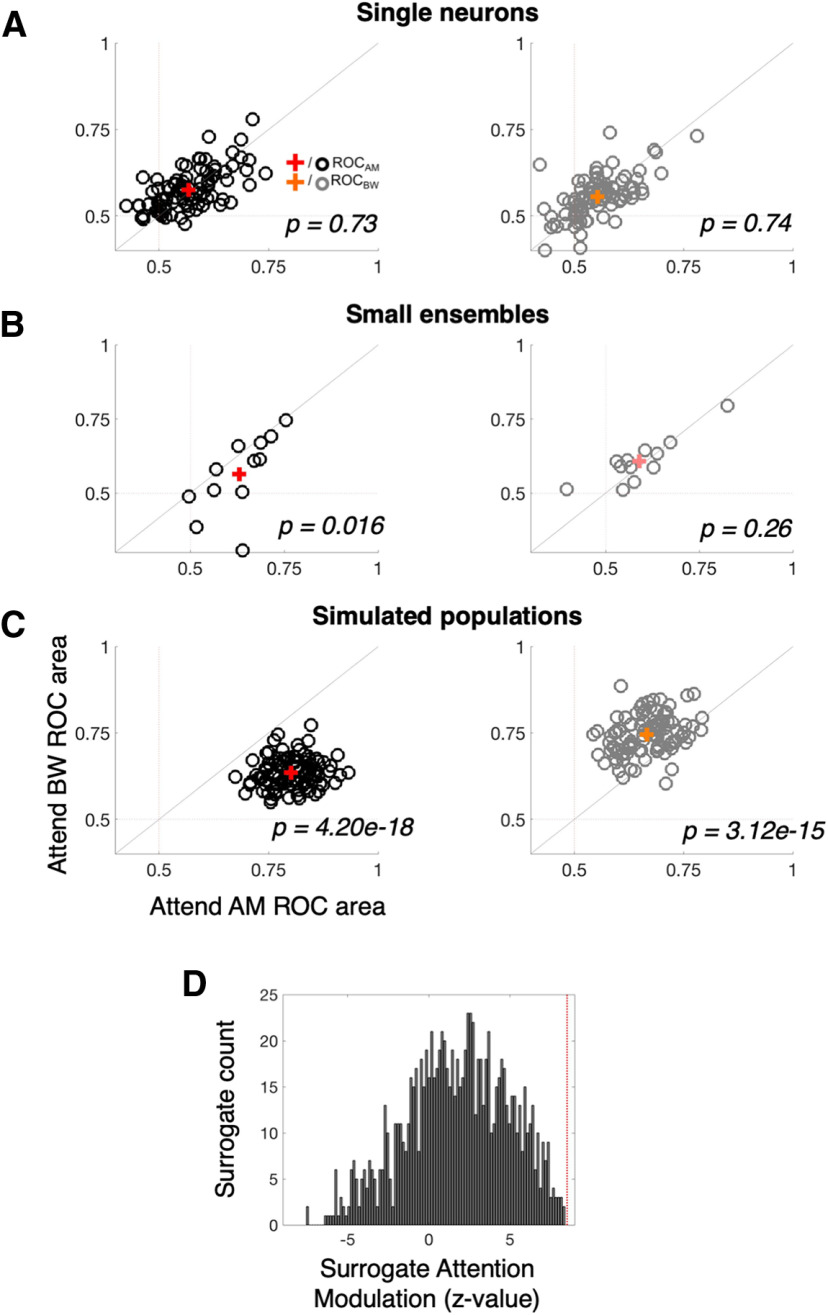
Qualitative effects of attention are apparent when comparing the population activity patterns across attend AM and attend BW conditions (e.g., Figs. 7B vs C, 8B,D vs C,E). We next quantified to what extent population encoding of relevant versus irrelevant stimulus features was affected by these changes. At the single-neuron FR level, we observe no effect of attention enhancing the representation of attended versus unattended features (Wilcoxon signed-rank test, p = 0.73 for ROC_AM, p = 0.74 for ROC_BW; Fig. 9A). However, in the small ensembles of simultaneously recorded neurons, subtle increases in the coding of the attended feature begin to emerge (Fig. 9B). Namely, the AM ROC area increases from 0.58 during attend BW to 0.63 during attend AM (Wilcoxon signed-rank test, p = 0.016) and the BW ROC area increases from 0.59 during attend AM to 0.61 during attend BW (Wilcoxon signed-rank test, p = 0.26). The attention-related increase is only statistically significant for AM ROC area. Moreover, using signal detection analyses on TDR population responses (see Materials and Methods) we find that simulated population projections onto two-dimensional weighted-feature space afford better decoding accuracy for each feature when it is attended (Fig. 9B). Across 100 simulated neural populations, the average ROC enhancement is 0.159 (0.77 vs 0.611) for AM ROC area and 0.108 (0.721 vs 0.612) for BW ROC area (Wilcoxon signed-rank test, p = 2.41e-30 and p = 3.08e-17, respectively).

Figure 9.

Population, not single neuron, representations sharpen with attention. A, Single-neuron ROC areas (similar to Fig. 6F,G) are compared between the attend AM (x-axis) and attend BW (y-axis) conditions. Black (gray) “o” markers represent single neuron average AM (BW) ROC values, with the red (orange) “+” representing the mean AM (BW) ROC value across the population. AM ROC and BW ROC distributions each lie along the unity line, indicating no average effect of attention (p = 0.73 and 0.74, respectively). B, Small ensemble ROC areas (one black and one gray marker for each of the 12 ensembles) exhibit small effects of attention. AM ROC values are significantly greater during attend AM (0.63 vs 0.58, p = 0.016). BW ROC values are higher during attend BW but the difference is not statistically significant (0.61 vs 0.59, p = 0.26). C, Simulated population ROC areas (one black and one gray marker for each of the 100 simulated populations of size n = 92 neurons) differ significantly between attention conditions, such that the average AM ROC area is 0.159 higher during attend AM than attend BW (red +; p = 2.41e-30) and the average BW ROC areas is 0.108 higher during attend BW than attend AM (orange +; p = 3.08e-17). D, The distribution of attention modulation values (the z-scored increase in ROC area for each feature when it is attended vs ignored) for 1000 surrogate populations is compared against the observed attention modulation in the neural data (vertical red line). Although surrogate populations, on average, exhibit a positive attention modulation (as evidence by the peak of the distribution well above 0), the attention modulation observed in the neural data exceeds that of any given surrogate population. This indicates high confidence that the finding in B constitutes a synergistic effect of attention on neural coding, above and beyond what would be expected if a weak attentional enhancement was present in a majority of individual neurons.

This dissociation between single-neuron and population attentional enhancement suggests a prioritized role for population-level representations in PSC during feature selective attention. Importantly, the difference in sensory sensitivity effects between single neurons and populations cannot be attributed to greater analytical power obtained by selective pooling over many neurons (Fig. 9C). Comparing the attentional modulation index (z score of ROC area difference of attended relative to unattended feature) of the neural data (9C, vertical red line) to that of 1000 surrogate populations, we find no overlap between our observed attentional enhancement and that expected by the simpler single-neuron and pairwise covariance properties. This suggests that our observed population enhancement of sound feature encoding constitutes an emergent effect, relying on higher-order correlations among A1 neurons.

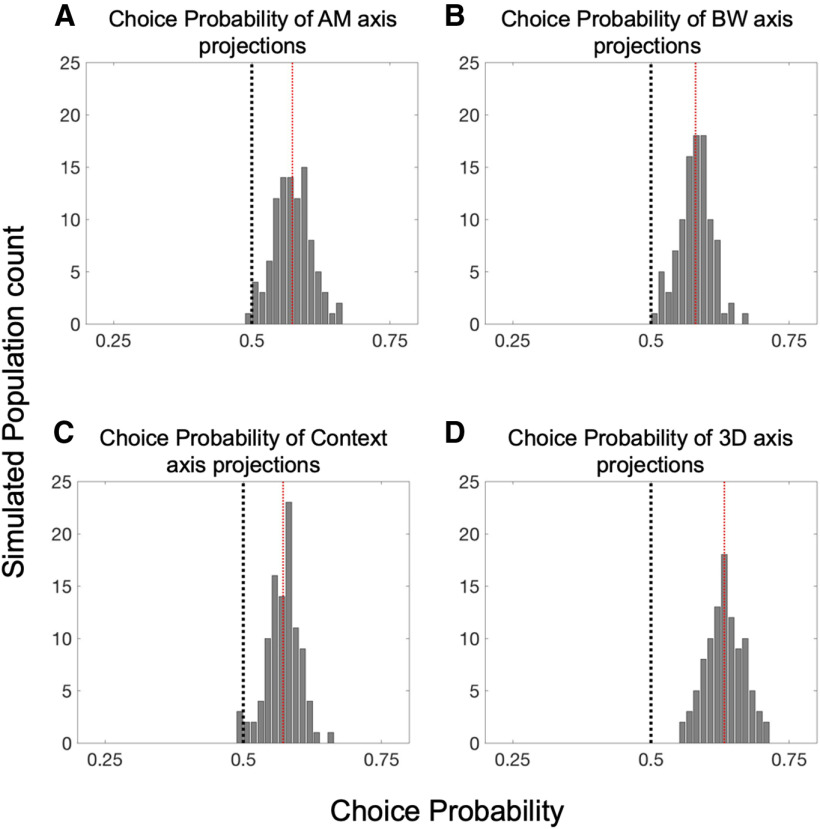
Finally, we analyzed how subjects' reported perceptual decision accounts for variance in trial-by-trial projections within the stimuli near perceptual threshold (AM₁–ΔBW₀ and AM₀–ΔBW₁; Fig. 10). In order to quantify these effects, we calculated the ROC area between correct and incorrect response distributions, a metric commonly referred to as choice probability (CP; Britten et al., 1992). In Figure 10A–C, we show the CP associated with variance along each task variable axis. For each single-axis projection, we find a significant difference from 0.5 in CP across 100 simulated neural populations (mean CP = 0.571, p = 1.9e-39 for AM axis projection; mean CP = 0.581, p = 4.82e-47 for BW axis projection; mean CP = 0.572, p = 1.37e-42 for context axis projection; Wilcoxon signed-rank test for each comparison). We also assessed CP for projections into the three-dimensional (AM × BW × context) subspace using a SVM algorithm to define a plane that best separates correct from incorrect trials' projections (Fig. 10D). This 3D-projection exhibits especially large CP value relative to projections onto the individual axes (mean CP = 0.633, p = 1.12e-61, Wilcoxon signed-rank test). Thus, choice-related activity accounts for some unique proportion of variance in the population data. Taken together with the attentional enhancements, the observation of performance-related population-level activity in A1 supports the notion that neurons in A1 act cooperatively to support auditory perception and decision-making.

Figure 10.

Population subspace projections correlate with trial-by-trial performance. A, The distribution of CP values across 100 simulated populations reveals a significant relationship between AM-axis projections and task performance, as evidenced by a mean CP across simulations of 0.573 (p = 1.90e-39). Likewise, B, C reveal that projections along the BW and context axes also correlate with task performance, with mean CP values of 0.581 and 0.572, respectively (p = 4.82e-47 and 1.37e-42). D, Projections of population activity into the full three-dimensional task variable subspace (AM × BW × context) are very reliably performance related, as evidenced by the entire distribution of CP values across simulated populations lying above 0.5, with a mean of 0.633 (p = 1.12e-61). Each significance test was a Wilcoxon signed-rank test with a null hypothesis of CP = 0.5.

Discussion

We find that single-neuron representations are insufficient to explain attention-related and choice-related activity in A1 neural populations. Instead, a population-level description is required to link sensory cortical activity and perception in A1. Although the finding that attention enhances population, but not single neuron, coding could simply reflect the amplification of a weak single-neuron signal, a surrogate population analysis (Elsayed and Cunningham, 2017) revealed that attention uniquely enhances sound coding at the population level.

Multiple recent studies of A1 highlight the importance of population-level representations (Downer et al., 2015, 2017a,b; Pachitariu et al., 2015; Francis et al., 2018). Population-level analyses can provide clear links between A1 activity and behavior, whereas single neurons may not (Christison-Lagay et al., 2017; Bagur et al., 2018; See et al., 2018; Yao and Sanes, 2018; Sadeghi et al., 2019). A critical question has remained unanswered, however: to what extent are these population-level findings an expected by-product of marginalizing across neurons (Sasaki et al., 2017)? For instance, in comparisons between active and passive states, in which only a single sensory feature matters for task performance, single neurons will likely resemble noisy versions of population representations, simply by virtue of there being very few stimulus parameters influencing single neurons (Gao et al., 2017). A1 neurons exhibit high dimensionality for sound features (O'Connor et al., 2005, 2010; Mesgarani et al., 2008; Sadagopan and Wang, 2009; Sloas et al., 2016) which can provide unambiguous population coding beyond that provided by any single neuron (Bizley et al., 2010). Indeed, it is well established that cortical neurons across sensory modalities have mixed selectivity for many stimulus features [e.g., orientation and contrast in visual cortex (Finn et al., 2007) and location and vibration frequency in somatosensory cortex (Nicolelis et al., 1998)]. In A1, mixed selectivity of up at least five sensory features has been demonstrated (Sloas et al., 2016). However, the effects of attention on sensory cortical neurons' encoding of these features chiefly involves experiments in which only a single feature is considered (Niwa et al., 2012b). Importantly, in the present report, sufficiently high dimensionality of the sensory and behavioral variables of the task allows for direct analysis of high-dimensional representation in single neurons and whether single-neuron representation suffices to explain population findings related to perception. We find that single neurons represent behavioral and sound variables in substantially “mixed” fashion, such that single-neuron FRs provide highly ambiguous information (Fusi et al., 2016). Only at the population level do the effects of attention and choice on neural activity become apparent (Figs. 9, 10). Such mixed selectivity/population-level primacy has previously been more linked with association and PFCs. However, previous studies of feature-selective and feature-based attention across the visual cortical hierarchy have revealed similarly complex single neuron results, suggesting that increasing stimulus and task complexity critically affects the interpretability of single neuron activity in sensory cortex (Chen et al., 2012; Ruff and Born, 2015; Schledde et al., 2017; Hembrook-Short et al., 2018). Additionally, single somatosensory and olfactory cortical neurons display distinct properties depending on task complexity (Miura et al., 2012; Gomez-Ramirez et al., 2014, 2016; Kim et al., 2015; Shiotani et al., 2020). Similar to the present study, neurons in these studies reflect the mixed selectivity commonly associated with “higher” cortical areas. Our findings therefore highlight the importance of studying sensory cortical neurons in sufficiently complex experimental conditions to uncover their function in complex environments.

In many previous studies in which single neurons were recorded while animals performed complex auditory tasks, single neuron encoding of target sounds is enhanced during engagement with, or attention toward, these sounds (Fritz et al., 2003; Niwa et al., 2012b; Buran et al., 2014; Carcea et al., 2017; Kuchibhotla et al., 2017; Schwartz and David, 2018). However, single neuron activity can fail to approximate the information encoded at the population level when more complex behavioral variables such as choice are considered (Christison-Lagay et al., 2017; Yao et al., 2019). The apparent gap between single-neuron and population-level coding can be explained if single neurons are considered as nonlinear contributors to the population as whole. Moreover, increasing experimental complexity likely widens this gap (Gao et al., 2017). We observe that context signals and sensory signals are apparently “tangled” in that the context and sensory signals are largely uncorrelated, leading to ambiguous single neuron codes (DiCarlo and Cox, 2007). Based on our population-level analyses, these tangled single neuron signals are disambiguated only at the population level. Future, similarly complex experiments, will allow a full description of the variables relating single neuron activity to population representations in sensory cortex.

The preponderance of single neurons whose activity is modulated by task context (i.e., attention condition) regardless of neurons' sensory coding bears further consideration. The abundance of neurons encoding task context is surprising for two reasons: (1) task context is more commonly encoded by A1 neurons than either sound feature although A1 is a sensory brain area; (2) the encoding of task context appears uncorrelated with A1 neurons' sensory function (Fig. 6D,E). Similarly, rat A1 neurons exhibit context encoding (Rodgers and DeWeese, 2014). In that study, context encoding is interpreted as important for flexible switching between “selection rules,” with remarkably similar context encoding between A1 and PFC. Considering our results alongside this previous study, a reasonable interpretation is that A1 not only participates in the representation of sensory information but also the behavioral context in which sounds are perceived (Mohn et al., 2021). Indeed, previous studies report task-related changes in single-neuron A1 activity that could be explained as providing crucial task context-related information (Buran et al., 2014; Jaramillo et al., 2014; Guo et al., 2017; Yao et al., 2019; Zempeltzi et al., 2020). Our finding that this context signal is independent of the sensory role of A1 neurons (Fig. 6D,E) suggests that task context coding (often expressed as shifts in baseline activity between task conditions) likely constitute more than an attention-related gain mechanism (Martinez-Trujillo and Treue, 2004), but rather reflect A1's role in more abstract, cognitive and/or behavioral aspects of hearing (Scheich et al., 2011; Kuchibhotla and Bathellier, 2018).

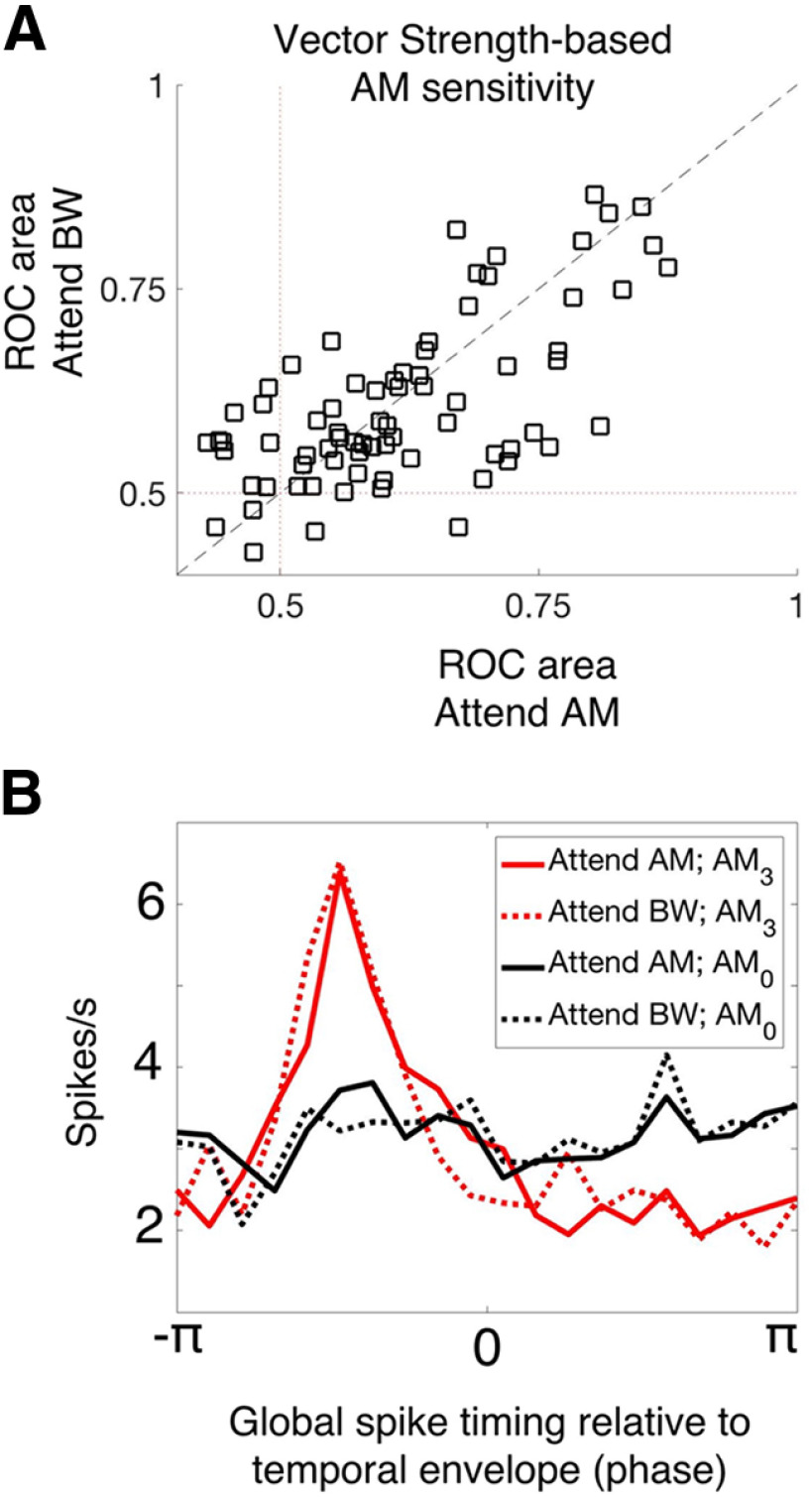
We exclusively used FR, as opposed to spike-timing measures of neural activity. However, A1 neurons encode temporal modulations with phase-locked spikes (Lu et al., 2001; Malone et al., 2007; Yin et al., 2011; Johnson et al., 2012). Task engagement significantly affects spike timing (Yin et al., 2014; Niwa et al., 2015), although in A1 these effects are modest relative to those observed for FR. We find a substantial proportion of neurons that phase lock to temporal sound envelopes, but no evidence of attention-related effects on phase locking (Fig. 11), suggesting that phase locking may not be relevant for feature-selective attention in this task in A1. It is important to note that we designed our task such that, even when attending to the spectral feature, many target sounds are temporally modulated as well, and therefore phase locking can signal the presence of a target in both attention conditions. Thus, the task may not sufficiently challenge the auditory system to drive attention-related changes in the temporal dynamics of A1 neurons' spiking. It remains unresolved whether attention affects temporal coding in other tasks or in other auditory areas, since FR dynamics provide a powerful, explicit code for temporal sound features that could help to disambiguate neural representations when FRs fail to do so. For instance, a task in which subjects must discriminate rather than detect temporal modulations may very well require attentional modulation of spike timing. Few studies have measured A1 activity during a temporal modulation discrimination task. Future studies may find significant attention-related changes in temporal response dynamics in A1 or other auditory structures.

Figure 11.

No evidence of attention-related changes in spike-timing-based sound encoding. A, We plot the vector strength-based neural sensitivity (ROC area) of each A1 neuron across attention conditions (attend AM, x-axis; attend BW, y-axis). There is no average difference in ROC area between conditions (Wilcoxon signed-rank test, p = 0.8849). B, We analyzed the tendency for neurons to fire spikes in the same phase relative to the temporal modulation. Global spike timing in response to the fully temporally modulated stimulus (AM₃, red) shows a prominent peak relative to the unmodulated stimulus (AM₀, black), indicating that A1 neurons tend to fire synchronous spikes relative to temporal modulation. We observe no effect of attention on this property of A1 neurons (solid lines vs dashed lines). These results indicate a lack of attentional modulation on the response dynamics of A1 neurons.

Some types of early sensory neural representations are more obviously high-dimensional – for instance, odorant coding (Laurent, 2002). Traditionally, primary sensory areas A1, S1, and primary visual cortex (V1) have been described in terms of a low-dimensional property, namely the placement of the stimulus on the sensory epithelium. However, no such “place” code exists for olfaction, since combinations of odorants comprise the “adequate stimulus” for olfaction and a two-dimensional sensory receptor surface ca not achieve a simple low-dimensional mapping of this combination space (Mathis et al., 2016; Herz et al., 2017). Like olfaction, auditory, somatic and visual perception also involve the combinations of many basic features (Walker et al., 2011; Gomez-Ramirez et al., 2014; Cowell et al., 2017; Franke et al., 2017; Lieber and Bensmaia, 2020). Therefore, when probed in high-dimensional conditions, all PSC fields may reflect a similar mechanism of representation to that observed in chemosensory areas. Therefore, in contrast to the classic descriptions, PSCs may be best described in terms of their complex, combinatorial, population-level representations.