Abstract
FamEvent is a comprehensive R package for simulating and modelling age-at-disease onset in families carrying a rare gene mutation. The package can simulate complex family data for variable time-to-event outcomes under three common family study designs (population, high-risk clinic and multi-stage) with various levels of missing genetic information among family members. Residual familial correlation can be induced through the inclusion of a frailty term or a second gene. Disease-gene carrier probabilities are evaluated assuming Mendelian transmission or empirically from the data. When genetic information on the disease gene is missing, an Expectation-Maximization algorithm is employed to calculate the carrier probabilities. Penetrance model functions with ascertainment correction adapted to the sampling design provide age-specific cumulative disease risks by sex, mutation status, and other covariates for simulated data as well as real data analysis. Robust standard errors and 95% confidence intervals are available for these estimates. Plots of pedigrees and penetrance functions based on the fitted model provide graphical displays to evaluate and summarize the models.
Keywords: ascertainment correction, mutation carrier probability, correlated time-to-event data, EM algorithm, family study designs, penetrance function estimation
1. Introduction
Family-based studies are efficient study designs, commonly used for linkage (gene mapping) and association (gene discovery) studies of both Mendelian and complex traits. Family-based designs, unlike population-based designs of unrelated individuals, are robust to population admixture and stratification that can distort disease-gene associations. Family-based design is also a very valuable approach to identify and characterize new pathogenic variants involved in complex human diseases through next generation sequencing technologies. Assessing such designs by simulation studies is an important aspect when planning a family study. We provide here a user-friendly R (R Development Core Team 2019) package for the simulation and estimation of time-to-event data under various family designs.
Nearly all of the currently available statistical software for time-to-event or age-at-onset data is only suitable for data collected under a random sampling scheme for independent individuals. The CRAN Survival Analysis task view (https://cran.r-project.org/web/views/Survival.html, version 2019-01-26) lists 264 CRAN packages related to survival data, including packages for estimating survival and hazard functions, fitting regression models, fitting of more complex models such as multistate models, and simulation. One exception is the coxme package (Therneau 2019) that can incorporate frailty terms to model family time-to-event data as well as to estimate the effects of other fixed covariates within a semi-parametric proportional hazards (PH) framework. However, it has functional limitations compared with FamEvent (Choi et al. 2019a): it does not simulate family data for age-at-onset outcomes, it adopts only a Gaussian distribution for the random effects, it does not provide age-dependent penetrance functions or various baseline hazard functions that retain the PH assumption. It also does not address important sources of bias including correction for non-random sampling and inferring missing genotypes and carrier probabilities. Drawbacks shared by both packages include limitations to right-censored data and the PH assumption. A specific shortcoming of FamEvent compared with the coxme package is its focus on fixed effects in the penetrance function estimation, so that mixed effects models are not yet provided. Although both packages can model family age-at-onset data, FamEvent provides substantially more functionality than the coxme package and corrects for two important sources of bias—sampling of families and missing data.
No other R packages that model family data, such as gap (Zhao 2019, 2007) or pbatR (Hoffmann and with contributions from Christoph Lange 2018), found in the Statistical Genetics task view (https://cran.r-project.org/web/views/Genetics.html, version 2019-01-26) provide functionalities for age-at-onset outcomes. On the other hand, some simulation programs have been proposed to simulate family or pedigree data, e.g., SimPed (Leal et al. 2005), SIMLA (Schmidt et al. 2005), PBAT (Lange and Laird 2002), SIMLINK (Boehnke 1986) (a comprehensive list is available at https://github.com/gaow/genetic-analysis-software/), but none of them can handle time-to-event outcomes. Our R package FamEvent is therefore an original contribution that fills a gap in simulating complex time-to-event data in the context of family designs and genetic studies. The simulated data can mimic real data obtained in these types of family studies. In addition, the estimation methods in FamEvent address important features for age-at-onset data from several common family-based designs. Thus, FamEvent provides considerably more advantages with few drawbacks all within one R package.
In the R package FamEvent, we provide methods to generate and model age-at-onset outcomes for families that harbor a genetic mutation. We implement three common family-based designs—population, high risk clinic and multi-stage designs—along with ascertainment correction for the estimation of age-dependent penetrance functions, specifically adapted to the sampling scheme, using a prospective likelihood. We also handle missing genotype data by providing mutation carrier probabilities for family members with missing genotypes and estimating age-dependent penetrance functions via an Expectation-Maximization (EM) algorithm. Plot methods are available for simulated family data and for fitted penetrance models, respectively. To construct pedigree plots, we implemented a pedigree function and its plot method built on kinship2 (Sinnwell and Therneau 2019) into the plot.simfam function to graphically display the pedigree structures of specified families with indication of the proband and affection and mutation carrier statuses of all family members. When mutation carrier status is missing, carrier probabilities can be displayed instead. Following penetrance model estimation, the plot.penmodel function presents both parametric and non-parametric estimates and their confidence intervals for the penetrance functions specific to gender and mutation status groups; parametric age-dependent penetrance curves are estimated from the specified parametric penetrance model by using penmodel or penmodelEM functions and non-parametric Kaplan-Meier estimates of the penetrance curves are obtained by implementing the survfit function built on the survival package (Therneau 2015).
Our comprehensive R package that simulates and models family data will enable development of methods to identify additional risk factors, adjust for interventions and produce unbiased disease risk estimates. In Section 2 we describe the family-based study designs implemented in FamEvent followed by details on the penetrance function and its estimation in Section 3.
Methodological details on ascertainment-corrected likelihoods, an EM algorithm, robust variance estimation and disease gene carrier probabilities are given in Section 4. Details on the key functions from the FamEvent package are provided in Section 5 and four motivating examples, including a real data analysis, are given in Section 6. Concluding remarks are given in Section 7.
2. Family-based study designs
Family-based designs are popular for studying heritable genetic diseases because high risk disease genes are rare in the general population. Often multiple family members are carriers of and affected by a disease gene, and can be identified from disease registries or high risk disease clinics. The study designs for sampling family data considered in FamEvent include population-based, clinic-based and two-stage sampling designs, as described in Table 1.
Table 1:
Family-based study designs implemented in FamEvent package.
| Design | Description and ascertainment criteria |
|---|---|
| POP | population-based design with affected probands whose mutation status can be either carrier or non-carrier. |
| POP+ | population-based design with affected and mutation carrier probands. |
| CLI | clinic-based design that includes affected probands with at least one parent and one sibling affected. |
| CLI+ | clinic-based design that includes affected and mutation carrier probands with at least one parent and one sibling affected. |
| Two-stage | two-stage sampling design that includes random sampling of families in the first stage and oversampling of high risk families in the second stage. |
In population-based studies, an affected family member (proband) leads to selection of the family into the study; the probands can be randomly sampled from the disease population regardless of their mutation status (POP design) or from the diseased and mutation carrier population (POP+ design). In clinic-based studies, the families are selected from high risk disease clinics; selection of families is not only based on a single proband but involves other affected family members. The CLI design samples families with an affected proband and at least two affected family members whereas the CLI+ design samples families with an affected mutation carrier proband and at least two affected members. The two-stage sampling is a popular sampling design method for oversampling high risks families, where the high risk families are defined as the families with multiple (at least two) affected members. In this design, families are sampled in two stages: the first sampling stage is based on the population-based study design and the second stage involves oversampling of high risk families.
For designing efficient studies, a two-stage family design can be used. In the first stage, case patients (i.e., probands) are selected and asked about their family disease history and then are stratified into different categories, e.g., high-, intermediate- and low-risks. In the second stage, case patients and their relatives are subsampled with different sampling probabilities that could depend on their risk category. For a fixed sample size, we can estimate the sampling probability for each stratum that minimizes the variance of the estimate of the parameter of interest. We illustrate a sample size determination for an optimal two-stage design in Section 6.3.
Families identified based on any of these study designs are not representative of the general population, since they tend to have higher disease risks from both genetic and non-genetic factors. Selection of families via each study design can lead to biased disease risk estimates, so adjustment for ascertainment is necessary. The ascertainment correction in the penetrance estimation is provided in Section 4.1.
3. Penetrance models
The risks of diseases arising from identified single or multiple genes often vary in the age at onset and are associated with individuals’ gender and mutation status, where the age-dependent disease risk is referred to as the penetrance. Penetrance in our R package is estimated using the cumulative distribution function given the age and gender of the individual for the disease or phenotypes associated with the gene of interest. A number of factors can impact penetrance such as mutation type, epigenetic factors, gender, modifier genes, etc. (Shawky 2014).
Parametric hazard regression models are implemented in penetrance studies as they can relate covariates, including genetic factors and gender, to the age-at-onset outcome. We first describe proportional hazard models, a most popular model for time-to-event data, which assumes no additional familial variations given the inherited disease gene. Additional variations to induce familial correlation due to unobserved genetic or environmental risk factors are modelled using two approaches: shared frailty model and two-gene model.
Proportional hazard models
Flexible functional forms are adopted for the baseline hazard function that retains the PH assumption and that also makes ascertainment correction easier.
The PH regression model with a baseline hazard h0(t) that relates an individual’s mutation status G and other measured covariates X to the age-at-disease onset can be expressed as follows:
| (1) |
where βX is the vector of regression coefficients for measured covariates X and βg is the regression coefficient for the genetic variable G. This PH regression model is used to estimate the probabilities of disease onset at age t via its cumulative distribution function (CDF)
| (2) |
where is the survival function at age at disease onset t. Penetrance functions for variable age at disease onset are based on this CDF, which conditions on measured covariates including mutation status and gender (Wijsman 2005).
The baseline hazard h0(t) is usually unspecified in PH models for evaluating covariate effects. For the purpose of estimating survival probabilities, a parametric assumption of the h0(t) is made. The possible choices for the parametric baseline hazard distribution are Weibull, log-logistic, log-normal, Gompertz, gamma, and more flexible distributions, including the log-Burr and a piecewise constant baseline. The generalized log-Burr distribution allows a flexible baseline that includes the Weibull model (η → ∞) or the log-logistic model (η = 1) as special cases (Lawless 2003; Kopciuk et al. 2009). The Weibull model is quite flexible but does have a monotonic functional form of the hazard whereas the log-logistic specification does not. The hazard and cumulative hazard functions are summarized in Table 2.
Table 2:
Possible choices of baseline hazard functions. f(t; λ, ρ) = λ(λt)ρ−1e−λt/Γ(ρ) is the density of gamma distribution; is the survival function of gamma distribution; ϕ and Φ are pdf and CDF of the standard normal distribution, respectively; for the piecewise constant hazard, 0 = τ0 < τ1 < ⋯ < τJ = ∞, Δj(t) = 0 if t < τj−1, t − τj−1 if τj−1 ≤ t < τj, or τj − τj−1 if t ≥ τj, j = 1, …, J.
| Distribution | Hazard h(t) | Cumulative hazard H (t) | |
|---|---|---|---|
| Weibull | ρλ(λt)ρ−1 | (λt)ρ | λ > 0 , ρ > 0 |
| Log-logistic | log{1 + (λt)ρ} | λ > 0 , ρ > 0 | |
| Log-normal | −∞ < λ < ∞ , ρ > 0 | ||
| Gompertz | λ > 0 , ρ > 0 | ||
| Gamma | f (t; λ, ρ)/S(t; λ, ρ) | −log S(t; λ, ρ) | λ > 0 , ρ > 0 |
| Log-Burr | η log{1 + (λt)ρ/η} | λ > 0 , ρ> 0 , η > 0 | |
| Piecewise constant | λi for t ∈ [τj−1, τj) | λj > 0 , j = 1,…, J |
Shared frailty models
The shared frailty model is used in conjunction with the PH model, where the frailty term acts multiplicatively on the baseline hazard function to describe the unknown common risks shared within family.
Let Tfi denote the age at disease onset for individual i in family f and Zf > 0 be the frailty shared within family f. The shared frailty models can be expressed as:
| (3) |
where h0(tfi) is the baseline hazard function and Xfi is a vector of covariates for individual i in family f and Gfi is a genetic covariate indicating carrier status of a mutated gene.
As the frailty is an unknown quantity, the penetrance function is obtained by integrating over the frailty distribution, G(z), where the indexes i and f are dropped for simplicity of notation,
| (4) |
where is the Laplace transform of the frailty distribution, is the cumulative baseline hazard function and X and G are their covariates and mutation status of a gene, respectively.
The penetrance function is determined by the choice of baseline hazard and frailty distributions with given covariate values and regression coefficients. The possible choices of the baseline functions and the frailty distributions and their Laplace transforms are listed in Tables 2 and 3, respectively. For example, if Weibull baseline and gamma frailty are assumed, the penetrance function can be obtained as
| (5) |
Table 3:
Possible choices of frailty distributions for familial correlation. ϕ(x; k) is the density function of the normal distribution with mean 0 and variance k.
| Distribution | Laplace transform | |
|---|---|---|
| Gamma | (1 + s/k)−k | k > 0 |
| Lognormal | k > 0 |
Two-gene models
In the two-gene model, we suppose that in addition to a major gene, G1, families share a second gene, G2, that induces familial correlation. G2 is considered as a covariate, that acts multiplicatively on the baseline hazard, but is completely unobserved. The two-gene model can be written, dropping indexes i and f, as:
| (6) |
where G1 and G2, respectively, indicate carrier (= 1) or non-carrier (= 0) status of the major and second genes.
Similarly, the penetrance function for the two-gene model is obtained depending on the choice of hazard function and the status of the second gene,
| (7) |
However, as the second gene G2 is unobserved, the penetrance functions can be obtained as a weighted sum over the two possible values of the second gene status.
| (8) |
where p(G2) is the probability of the second gene status, which is determined by the assumed allele frequency, and G2 takes values of 1 or 0, representing carrier or non-carrier, respectively.
4. Methods
4.1. Ascertainment correction
Assuming, without loss of generality, that the affected family member (proband) who led to selection of the family into the study is a disease gene carrier, then ascertainment correction for the selection process takes one of two forms. If the proband is randomly sampled from the population (POP or POP+ design), say through a disease registry, then ascertainment correction depends only on this individual. If the proband is selected from a high risk disease clinic (CLI or CLI+ design), then ascertainment correction involves other, possibly affected family members. In the prospective likelihood method, the ascertainment correction is based solely on the probability of individuals being affected before their age at examination (Choi et al. 2008).
For family f of size nf, we define , and as the vector forms that represent their phenotypes (disease outcomes), genotypes and covariates, respectively. The contribution of family f to the ascertainment-corrected prospective likelihood is
| (9) |
where we assume that P (Af|Df, Gf, Xf) is 1 if family f qualifies for ascertainment (Af), and 0 otherwise. The numerator, regardless of family study design, assumes conditional independence of family members’ phenotypes given their genotypes, and is specified as
| (10) |
Ascertainment correction of family f from the population-based designs (POP or POP+) depends on the proband (p) in family f being affected before his or her current age at examination , and hence, the denominator P (Af|Gf, Xf) can be written as
| (11) |
where and represents the proband’s genotype and observed covariates in family f. For the clinic-based designs (CLI or CLI+), the ascertainment correction is determined by three additional family members—another affected sibling and at least one affected parent.
By the conditional independence assumption of disease status given genotype information, the denominator for the clinic-based designs is given by
| (12) |
where indices fp, fs, ff, fm represent the proband, proband’s sibling, father and mother in family f, respectively.
In two-stage sampling, the ascertainment correction is based on the sampling weights derived from an inverse probability of sampling families, which are implemented into the composite likelihood as a weighted product of ascertainment-corrected likelihoods corresponding to each family (Choi and Briollais 2011; Lawless et al. 1999). The likelihood contribution of n families sampled from two-stage sampling is written as
| (13) |
where Lf is the ascertainment-corrected likelihood for family f by a population-based design used at the first stage and wf represents the sampling weight for family f at the second stage, which is obtained by the inverse probability of sampling family from the two stages of sampling.
4.2. EM algorithm for missing genotype data
In addition to ascertainment or selection correction, family members with phenotype (disease outcome) but no genotype information can be included via an Expectation-Maximization (EM) algorithm. Given their family’s observed genotypes and phenotypes, the probabilities of an individual’s possible genotypes are computed in the Expectation or E-step. In the Maximization or M-step, the model parameters are estimated by maximizing a weighted log-likelihood. The conditional genotype probabilities found in the E-step form these weights.
The vector of genetic covariates in family f, Gf, is partitioned into observed genotypes and missing genotypes . Both the measured covariates Xf and phenotypes Df are fully observed, with the phenotypes subject to right censoring. Then the single-iteration EM is implemented as follows:
E-step Compute the possible genotype probabilities for each individual i with missing genotype in family f as
| (14) |
where can take the value 1 or 0 to represent a carrier or non-carrier of the mutated gene, respectively, and their probabilities and can be obtained empirically from the family data or analytically from the assumed penetrance model. The empirical carrier probabilities (non-carrier probabilities just as the complementary probability) can be obtained with observed genotype and phenotype information for each subset of the data defined by Df, Xf, after excluding the probands. Based on the penetrance model, these carrier probabilities are obtained as the posterior distribution with the assumed or estimated allele frequency (as shown in Section 4.4). For individuals with known carrier status, their weights are one. Then, the conditional expectation of the log-likelihood function of the complete data given the observed data (D, X, Go) can be written as a weighted log-likelihood which has the form
| (15) |
where is the set of all possible genotypes for individual i in family f.
M-step Maximize the weighted log likelihood to obtain the parameter estimates in the model.
No iteration between the E and M steps is necessary when the empirical carrier probability is used as the possible genotype probabilities only need to be calculated once in the E-step. Otherwise, the E-M steps iterate until convergence.
4.3. Robust variance estimation
To account for familial correlation, as our penetrance model assumes conditional independence of the individuals in the family, the robust variance estimator of the parameter estimates is provided in a ‘sandwich’ form (White 1982) as
| (16) |
where I0(θ) is the observed information matrix obtained from
ℓf(θ) is the ascertainment-corrected log-likelihood for family f and .
The robust variance-covariance matrix then can be consistently estimated by evaluating the at the maximum likelihood estimates.
4.4. Disease gene carrier probabilities
Mutation carrier probabilities for relatives with missing genotype information can be estimated using observed genotypes within the families or alternatively, with the addition of phenotype information. The carrier probability can be calculated based on only observed genotypes using Mendelian transmission probabilities or using data-driven probabilities empirically calculated from the aggregated data for each subgroup based on relation, proband’s mutation status, mode of inheritance, disease status and disease-allele frequency in the population. It can be also obtained based on both observed genotype and phenotype information using the penetrance model fit.
The carrier probability for individual i conditional on the observed phenotype and carrier status of his or her family members is calculated by
| (17) |
where Gi indicates the carrier status of individual i and Go represents the observed carrier status in his or her family members, Di represents the observed phenotype (ti; δi) of individual i in terms of age at disease onset ti and disease status indicator δi (1 for affected individuals and 0 for unaffected individuals).
5. Package description
The R Package FamEvent is available for download from CRAN (The Comprehensive R Archive Network 2019). This package will appeal to users who want to simulate complex pedigree data for age-at-onset phenotypes for families who carry a major gene and/or users who want to estimate disease gene penetrance functions using their own family data with correction for selection bias and missing genotype information. Plotting functions permit visual examination of individual pedigrees, the true penetrance functions and the estimated penetrance functions based on the fitted model. Mutation carrier probabilities for individuals with missing genotype information are estimated using information on family members genotypes and possibly phenotypes. The main functions used in FamEvent are summarized in Table 4 and their usage in practice is described in this section.
Table 4:
Description of main functions in FamEvent package.
| Functions | Description |
|---|---|
| carrierprob | computes the carrier probability from observed genotype or phenotype data or from the penetrance model fit. |
| fampower | computes the power of detecting genetic effect in the penetrance model based on a family-based simulation study. |
| penetrance | estimates the cumulative disease risks (penetrances) and confidence intervals at given age(s) based on the fitted penetrance model. |
| penmodel | fits penetrance models for complete family data. |
| penmodelEM | fits penetrance models for family data with missing genetic information. |
| penplot | plots the penetrance functions given the values of baseline parameters and regression coefficients and choices of baseline and frailty distributions. |
| simfam | simulates family data. |
The package in R is installed and loaded in the usual way:
R> install.packages(“FamEvent”) R> library(“FamEvent”)
5.1. Penetrance curves
The function penplot enables researchers to see the shape of the penetrance function and to choose appropriate penetrance functions for checking the performance of a penetrance model or planing a simulation study.
The shape of penetrance functions is determined by choosing the baseline hazard distribution (base.dist) with their parameter values (base.parms), the regression coefficient values for gender and major gene (vbeta) and the source of residual familial correlation (variation). Familial correlation can be induced by either a shared frailty (variation = “frailty”) or a second gene shared within the family (variation = “secondgene”). The default is “none” implying that event times are independent given major genotypes. When variation = “frailty”, the choice of the frailty distribution (frailty.dist) and the variance of the frailty distribution (depend) should be specified.
For example, the following function call will display the penetrance functions and return penetrance estimates by age 70 specific to gender and mutation-status, based on the Weibull baseline distribution with scale parameter, λ, set to 0.01, shape parameter, ρ, set to 3 and familial correlation induced by a shared frailty within each family which follows a gamma distribution with mean 1 and variance 1 that was specified by the argument depend = 1. We can also specify the minimum age of disease onset agemin for the penetrance function to start.
R> penplot(base.parms = c(0.01, 3), vbeta = c(−1.3, 2.35),
+ base.dist = “Weibull”, frailty.dist = “gamma”, variation = “frailty”,
+ depend = 1, agemin = 20)
Call: gamma frailty with Weibull baseline
Penetrance by age 70:
male-carrier female-carrier male-noncarr female-noncarr
0.26319239 0.56723000 0.03294418 0.11111111
5.2. Family data generation
The simfam function generates data for all family members, including their age, gender, family relation, disease gene mutation status, and times to an event, based on the penetrance model associated with mutated genes and gender as we described in Section 3. The principles of generating family data were described in Choi et al. (2008). Each family consists of three generations—two parents and their offspring whose number ranges in size from 2 – 5, one of whom is the proband. Each offspring has a spouse and their children whose number ranges in size from 2 – 5. The age difference between the second and third generations is assumed to be 20 years on average. Given the study design, the proband’s mutation status is generated first and their age at onset generated conditional on the mutation status. Other family members’ mutation statuses are determined based on the proband’s status and then their ages at onset are generated. Finally, their affection status is determined if their ages at onset are before their current age. This procedure is repeated until the ascertainment criteria specified by the study design is satisfied.
The standard code with default values for generating family data is
R> simfam(N.fam, design = “pop”, variation = “none”, interaction = FALSE, + base.dist = “Weibull”, frailty.dist = NULL, base.parms, vbeta, + depend = NULL, allelefreq = c(0.02, 0.2), dominant.m = TRUE, + dominant.s = TRUE, mrate = 0, hr = 0, probandage = c(45, 2), + agemin = 20, agemax = 100)
With the simfam function, family data can be simulated under various family study designs (design) listed in Table 1. For the two-stage design (design = “twostage”), the proportion of high risk families to be included in the sample should be specified by argument hr. Simulating families under the clinic-based (“cli” or “cli+”) or the two-stage designs can be slower since the ascertainment criteria for the high risk families are diffcult to meet in such settings. In particular, the “cli” design could be slower than the “cli+” design since the proband’s mutation status is randomly selected from a disease population in the “cli” design, so his or her family members are less likely to be mutation carriers and to be affected, whereas when the probands are all mutation carriers (“cli+”), their family members have higher chance to be carriers and affected by disease. Therefore, the “cli” design requires more iterations to sample high risk families than the “cli+” design. All simulations that include variation = “frailty” could be slower in order to generate families with specific familial correlations induced by the chosen frailty distribution.
Popular hazard function distributions—such as Weibull, loglogistic, Gompertz, lognormal, gamma, or logBurr—are available to generate the baseline hazard distribution. Residual familial correlation can be created by incorporating a frailty term (variation = “frailty”) with a choice of lognormal or gamma distribution or via a two-gene model (variation = “secondgene”). For the major and possibly second gene, users can specify if the genetic model is dominant or recessive (dominant.m for the major gene and dominant.s for the second gene) and their population allele frequencies (allelefreq). Additional parameter option values can fix the proportion of missing genotypes (mrate) and the minimum (agemin) and maximum (agemax) age of disease onset.
Details of selected arguments for the simfam function are described in Table 5.
Table 5:
Description of arguments for simfam function.
| Argument | Description |
|---|---|
| N.fam | Number of families to generate. |
| design | Family-based study design. Possible choices are “pop”, “pop+”, “cli”, “cli+”, “twostage”. |
| variation | Source of familial correlation. Possible choices are “frailty” for frailty shared within families, “secondgene” for second gene variation, “none” for no familial correlation given major genotypes. |
| interaction | Logical; if TRUE, allows the interaction between gender and major gene. |
| depend | Variance of the frailty distribution. Dependence within families increases with depend value. |
| base.dist | Choice of baseline hazard distribution. Possible choices are “Weibull”, “loglogistic”, “Gompertz”, “lognormal”, “gamma”, “logBurr”. |
| base.parms | Vector of baseline parameter values. |
| vbeta | Vector of regression coefficients for gender, major gene, interaction between gender and major gene (if interaction = TRUE), and second gene (if variation = “secondgene”). |
| frailty.dist | Choice of frailty distribution. Possible choices are “gamma”, “lognormal” or NULL. |
| mrate | Proportion of missing genotypes; value between 0 and 1. |
| hr | Proportion of high risk families, which include at least two affected members, to be sampled from the two stage sampling (design = “twostage”); value should lie between 0 and 1. |
| probandage | Vector of mean and standard deviation of the proband’s age. |
| agemin | Minimum age of disease onset. |
| agemax | Maximum age of disease onset. |
The following example shows the use of simfam function to generate 200 families using set.seed(4321) from the study design “pop+”, where families are sampled based on affected and mutation carrier probands. The ages to disease onset are assumed to follow a Weibull baseline hazard distribution with the effects of gender and mutation status set at βs = −1.13, βg = 2.35, respectively. The familial correlation is due to a shared frailty following a gamma distribution with mean 1 and variance 1. The allele frequency of the major gene is assumed to be 0.02.
R> fam <- simfam(N.fam = 200, design = “pop+”, variation = “frailty”, + base.dist = “Weibull”, frailty.dist = “gamma”, depend = 1, + base.parms = c(0.01, 3), vbeta = c(−1.13, 2.35), allelefreq = 0.02, + agemin = 20)
Table 6 presents the simulated data for the first family, which includes the founders, probands, ages at disease onset, gene carriers assuming a dominant model as well as other variables needed for estimation.
Table 6:
The simulated data for family 1 from simfam function
| famID | indID | gender | motherID | fatherID | proband | generation | majorgene | secondgene | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 2 | 0 |
| 2 | 1 | 2 | 0 | 0 | 0 | 0 | 1 | 2 | 0 |
| 3 | 1 | 3 | 0 | 2 | 1 | 1 | 2 | 2 | 0 |
| 4 | 1 | 4 | 1 | 0 | 0 | 0 | 0 | 3 | 0 |
| 5 | 1 | 9 | 0 | 3 | 4 | 0 | 3 | 2 | 0 |
| 6 | 1 | 10 | 1 | 3 | 4 | 0 | 3 | 3 | 0 |
| 7 | 1 | 11 | 1 | 3 | 4 | 0 | 3 | 3 | 0 |
| 8 | 1 | 12 | 1 | 3 | 4 | 0 | 3 | 3 | 0 |
| 9 | 1 | 13 | 1 | 3 | 4 | 0 | 3 | 2 | 0 |
| 10 | 1 | 5 | 0 | 2 | 1 | 0 | 2 | 2 | 0 |
| 11 | 1 | 6 | 1 | 0 | 0 | 0 | 0 | 3 | 0 |
| 12 | 1 | 14 | 0 | 5 | 6 | 0 | 3 | 3 | 0 |
| 13 | 1 | 15 | 0 | 5 | 6 | 0 | 3 | 2 | 0 |
| 14 | 1 | 16 | 0 | 5 | 6 | 0 | 3 | 3 | 0 |
| 15 | 1 | 7 | 0 | 2 | 1 | 0 | 2 | 2 | 0 |
| 16 | 1 | 8 | 1 | 0 | 0 | 0 | 0 | 3 | 0 |
| 17 | 1 | 17 | 0 | 7 | 8 | 0 | 3 | 3 | 0 |
| 18 | 1 | 18 | 0 | 7 | 8 | 0 | 3 | 2 | 0 |
| ageonset | currentage | time | status | mgene | relation | fsize | naff | weight | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 103.76925 | 69.19250 | 69.19250 | 0 | 1 | 4 | 18 | 2 | 1 |
| 2 | 64.88982 | 67.31119 | 64.88982 | 1 | 1 | 4 | 18 | 2 | 1 |
| 3 | 45.84891 | 47.57119 | 45.84891 | 1 | 1 | 1 | 18 | 2 | 1 |
| 4 | 269.71990 | 47.37403 | 47.37403 | 0 | 0 | 6 | 18 | 2 | 1 |
| 5 | 69.78355 | 27.80081 | 27.80081 | 0 | 1 | 3 | 18 | 2 | 1 |
| 6 | 192.09392 | 25.34148 | 25.34148 | 0 | 0 | 3 | 18 | 2 | 1 |
| 7 | 124.54791 | 23.42188 | 23.42188 | 0 | 0 | 3 | 18 | 2 | 1 |
| 8 | 115.05352 | 25.20730 | 25.20730 | 0 | 0 | 3 | 18 | 2 | 1 |
| 9 | 117.02180 | 23.33795 | 23.33795 | 0 | 1 | 3 | 18 | 2 | 1 |
| 10 | 66.73818 | 40.44924 | 40.44924 | 0 | 1 | 2 | 18 | 2 | 1 |
| 11 | 236.29150 | 47.44871 | 47.44871 | 0 | 0 | 7 | 18 | 2 | 1 |
| 12 | 90.52633 | 18.75310 | 18.75310 | 0 | 0 | 5 | 18 | 2 | 1 |
| 13 | 75.09973 | 18.17504 | 18.17504 | 0 | 1 | 5 | 18 | 2 | 1 |
| 14 | 92.65091 | 18.49978 | 18.49978 | 0 | 0 | 5 | 18 | 2 | 1 |
| 15 | 69.86995 | 43.10898 | 43.10898 | 0 | 1 | 2 | 18 | 2 | 1 |
| 16 | 179.44599 | 42.12909 | 42.12909 | 0 | 0 | 7 | 18 | 2 | 1 |
| 17 | 143.52790 | 19.55723 | 19.55723 | 0 | 0 | 5 | 18 | 2 | 1 |
| 18 | 57.56951 | 20.63106 | 20.63106 | 0 | 1 | 5 | 18 | 2 | 1 |
The data frame includes columns famID, indID, motherID, fatherID for family, individual, mother and father IDs, respectively; generation which takes values 1, 2, 3 or 0, where 0 indicates spouses; and gender indicating males (= 1) and females (= 0). majorgene indicates the genotype status of a major gene of interest, denoting 1 for AA, 2 for Aa and 3 for aa, where A is a disease-causing allele. ageonset is the age of disease onset generated by the penetrance model shown in (3). However, we do not observe ageonset beyond the current age (currentage), so time takes the minimum value of ageonset and currentage and status indicates disease status at current age, i.e., 1 if the disease is observed by current age and 0 otherwise. mgene records the mutated gene carrier status derived from the major gene genotype, indicating 1 if carrier of disease gene, 0 otherwise. relation represents the family members’ relationship with the proband as described in Table 7.
Table 7:
Family relation code used in simulated data.
| Relation | Description |
|---|---|
| 1 | Proband (self) |
| 2 | Brother or sister |
| 3 | Son or daughter |
| 4 | Parent |
| 5 | Nephew or niece |
| 6 | Spouse |
| 7 | Brother or sister in law |
In addition, data include the family size fsize, the number of affected family members naff and sampling weight weight for each family. For example, the family with famID = 1 has 18 members and includes only one affected individual in addition to the proband. The individual with indID = 3 is the proband whose current age is 47 years old, he was affected (status = 1) at age 47 and is a mutation carrier (mgene = 1) with genotype Aa (majorgene = 2). Figure 1 also graphically displays the pedigree of this family, where the red colour indicates the proband, right shading indicates mutation carriers, non-shading for non-carriers, left filled symbol indicates affected by the disease and non-filled symbol for unaffected by the disease.
Figure 1:
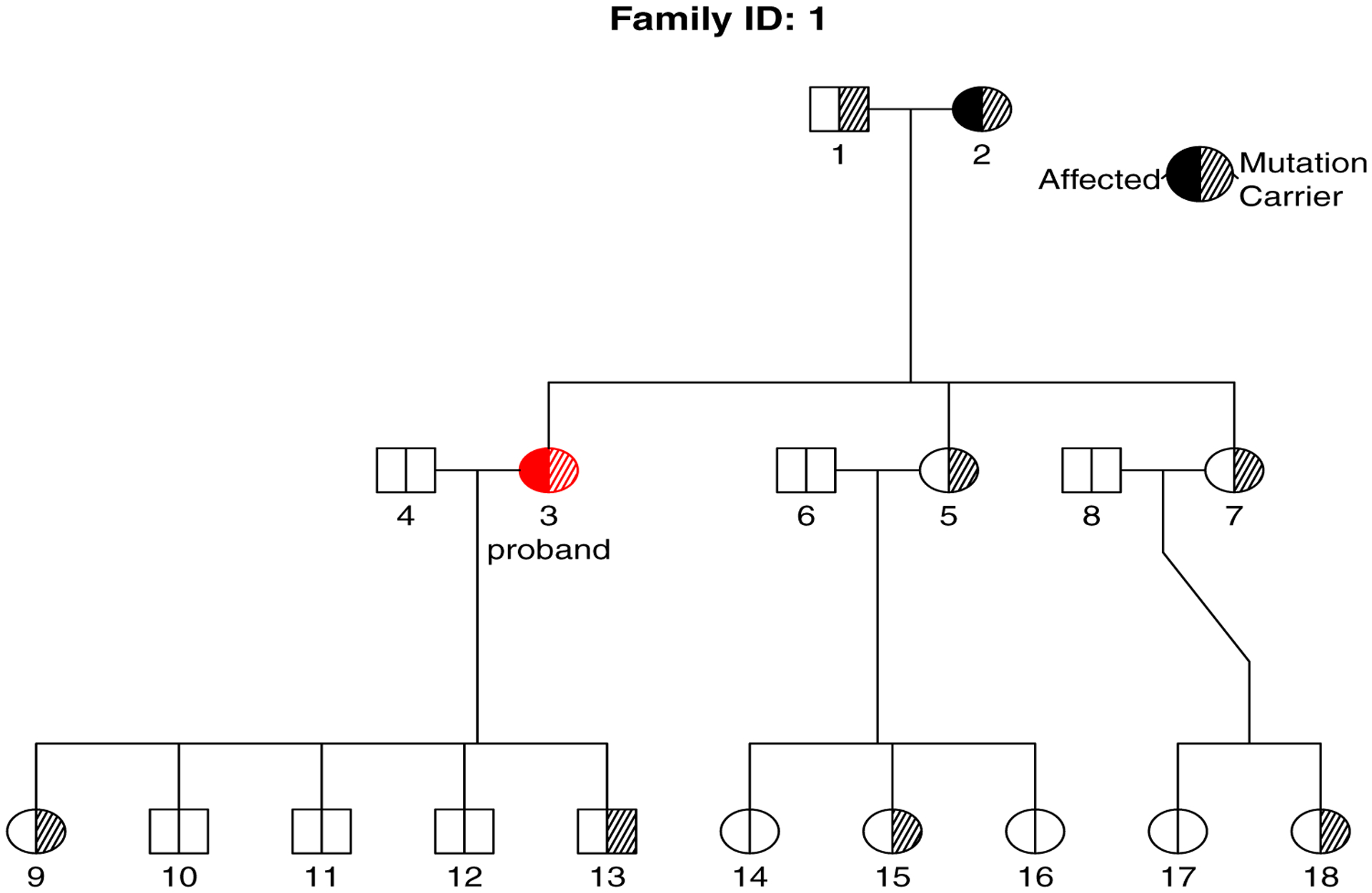
Pedigree plot generated by plot function for a selected family.
The output of simfam function is an object of class ‘simfam’. The ‘simfam’ class has its own summary and plot methods: summary function prints the summary of generated data and plot function provides the pedigree plots of specified families with indication of family members’ affection status and mutation carrier status. Examining several individual pedigrees is helpful for assessing the genetic transmission model, number of carriers and affected individuals within the simulated families.
R> summary(fam) Study design: pop+ Baseline distribution: Weibull Frailty distribution: gamma Number of families: 200 Average number of affected per family: 2.02 Average number of carriers per family: 5.88 Average family size: 15.27 Average age of onset for affected: 43.31 Sampling weights used: 1 R> plot(fam, famid = 1, pdf = TRUE, file = “pedigreeplot.pdf”)
5.3. Penetrance model estimation
The penetrance model is estimated with either the penmodel function for complete genetic data or the penmodelEM function in presence of missing genetic data using the EM algorithm. These functions provide the model parameter estimates with their conventional standard errors based on the Hessian matrix or robust standard errors based on the sandwich variance formula if robust = TRUE. The output of penmodel or penmodelEM is an object of class ‘penmodel’, which has a list with elements of model parameter estimates, their covariance matrix, standard errors, (or robust covariance matrix, robust standard errors if robust = TRUE is specified).
The corresponding program codes for fitting a proportional hazard model for complete or missing genetic data are:
penmodel(formula, cluster = “famID”, gvar = “mgene”, parms, cuts = NULL, data, design = “pop”, base.dist = “Weibull”, agemin = NULL, robust = FALSE) penmodelEM(formula, cluster = “famID”, gvar = “mgene”, parms, cuts = NULL, data, design = “pop”, base.dist = “Weibull”, agemin = NULL, robust = FALSE, method = “data”, mode = “dominant”, q = 0.02)
Both functions take the formula expression as used in other regression models with time-to-event data using the Surv function and covariates, name of the cluster variable (cluster), name of the genetic variable (gvar), initial parameter values including baseline parameters and regression coefficients (parms), family data set (data), as well as specification of the family study design (design), baseline hazard distribution (base.dist) options, allowing for the same or different choice of baseline hazard from the simulated data. In addition to the options for base.dist listed in Table 5, base.dist = “piecewise” fits a piecewise constant baseline hazard function with specified cuts that define the intervals where the hazard function is constant. A prospective likelihood that corrects for ascertainment is used with the type of correction depending on the family study design specified in the design argument.
When imputation of missing genotype is needed, the penmodelEM function implements the EM algorithm to estimate the disease gene carrier probabilities for family members who are missing this key variable. Two methods are available: if sufficient genotype information is available within every family, then carrier probabilities can be empirically calculated from the aggregated data for each subgroup based on generation and proband’s mutation status (method = “data”) otherwise they can be calculated based on Mendelian transmission probabilities by selecting method = “mendelian” with mode of inheritance (mode) specifying as either “dominant” or “recessive” and the allele frequency (q) as a value between 0 and 1.
The output of penetrance model fit includes the parameter estimates, their variance covariance matrix, the corresponding standard errors (SEs), the log-likelihood and Akaike information criterion (AIC) values at its maximum value. In addition, robust SEs and ‘sandwich’ variance covariance matrix are provided if robust = TRUE. Robust SEs could be smaller than the conventional SEs when the sample sizes are small or a parameter is estimated from effectively few non-zero covariate values (Fay and Graubard 2001). When sample sizes are small, the robust SE can be biased downward and some particular techniques can be used to correct this bias (see for example, Imbens and Kolesár (2016)). Conventional SEs could be considered instead although we do not expect a large difference from the robust SE.
The ‘penmodel’ class has its own print, summary and plot methods. The summary method returns and displays the model parameter estimates of transformed baseline parameters and regression coefficients with their SEs (or robust SEs if robust = TRUE), t statistics and corresponding two-sided p values. The plot method produces a graph of estimated penetrance functions for four subgroups by gender and mutation status in different colours along with Kaplan-Meier curves from family data used for fitting the model excluding probands, in order to naïvely correct for ascertainment. Thus, this plot displays both parametric and non-parametric estimates of penetrances from the minimum to the maximum age at onset, along with their 95% confidence intervals if conf.int = TRUE.
Continuing our example from Section 5.2, we fit the data set consisting of 200 families (data = fam) to a penetrance model for the right censored time-to-event outcome, Surv(time, status), with two covariates, gender and mgene, assumed a Weibull baseline hazard distribution and accounted for the family study design (design = “pop+”) used to sample the families. We specified the name of the cluster variable as cluster = “famID”, the name of genetic variable as gvar = “mgene” and the initial values of the baseline parameters, λ and ρ, as well as the gender and mutation effects on the baseline hazard function as parms = c(0.01, 3, −1.13, 2.35). The summary of the model fit is given below and the plot function generates the penetrance curves shown in Figure 2.
Figure 2:
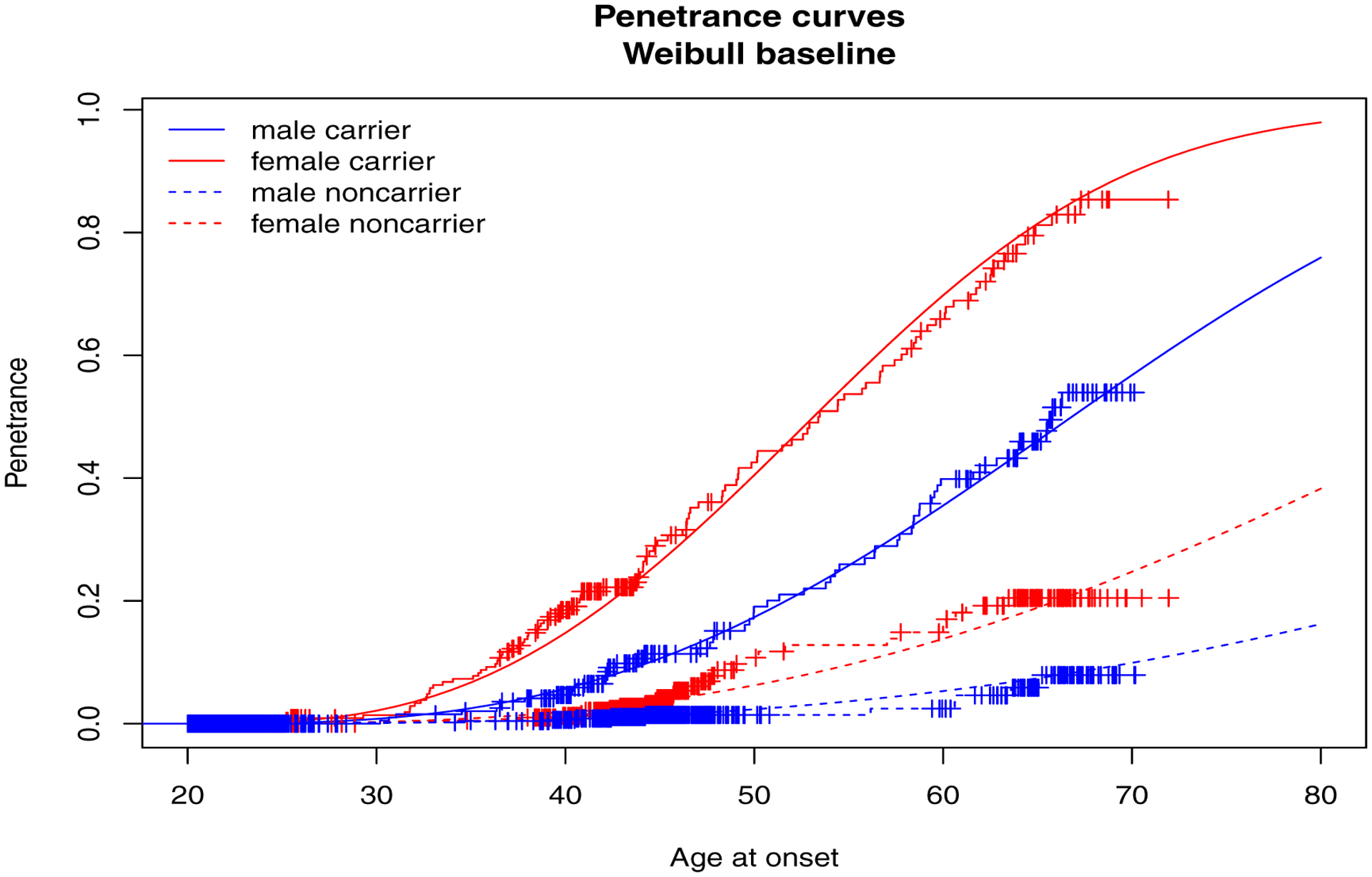
Penetrance curves estimated with ascertainment correction.
R> fit <- penmodel(Surv(time, status) ~ gender + mgene, cluster = “famID”,
+ gvar = “mgene”, parms = c(0.01, 3, −1.13, 2.35), data = fam,
+ design = “pop+”, base.dist = “Weibull”, robust = TRUE)
R> summary(fit)
Estimates:
Estimate Std. Error Robust SE t value Pr(>|t|)
log(lambda) −4.345 0.06489 0.06177 −70.350 0.009049 **
log(rho) 1.066 0.04075 0.03813 27.947 0.022770 *
gender −1.003 0.14877 0.15130 −6.628 0.095336 .
mgene 2.085 0.17462 0.16008 13.023 0.048790 *
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ‘ 1
R> plot(fit, conf.int = FALSE, add.KM = TRUE, MC = 100)
Estimates:
log(lambda) log(rho) gender mgene
−4.345359 1.065674 −1.002791 2.084711
Penetrance (%) by age 70:
male-carrier female-carrier male-noncarr female-noncarr
0.56770489 0.89833272 0.09902695 0.24742489
5.4. Age-specific penetrance estimation with confidence intervals and standard errors
At given age(s) and fixed covariate values, the penetrance function provides penetrance estimates with 95% confidence intervals (CIs) and SEs of the penetrance estimates through Monte Carlo (MC) simulations of the estimated penetrance model. Provided a model fit from penmodel or penmodelEM, parameter estimates of both the transformed baseline parameters and regression coefficients along with their variance-covariance matrix are used as the inputs to a multivariate normal distribution. Based on these inputs, MC = n sets of parameters are generated for given age(s) and fixed covariates and their corresponding penetrance estimates calculated. For baseline parameter estimation, a log transformation is applied to both scale and shape parameters (λ, ρ) for the Weibull, loglogistic, Gompertz, gamma baseline distributions, to (λ, ρ, η) for the log-Burr distribution and to the piecewise constant parameters for a piecewise baseline hazard. But for the lognormal baseline distribution, the log transformation is applied only to ρ, not to λ, which represents the location parameter for the normally distributed logarithm.
Empirical estimates of the the 95% CIs at given age(s) are based on the 2.5th and 97.5th percentiles of the penetrance functions estimated from the n simulated data values. The SE of the penetrance estimate, also for given age(s), is calculated via the standard deviation of the n simulated penetrance functions. Both the 95% CIs and SEs are obtained for fixed covariates at the given age(s). For example, using the penetrance model fitted to the 200 families in Section 5.3, the penetrance estimates by age 50, 60, and 70 for male mutation carriers fixed = c(1, 1) can be obtained using 100 MC simulations (MC = 100) as follows:
R> penetrance(fit, fixed = c(1,1), age = c(50, 60, 70), CI = TRUE, MC = 100) Fixed covariate values: gender = 1 mgene = 1 age penentrance lower upper se 1 50 0.1733465 0.1383407 0.2106344 0.01990850 2 60 0.3551920 0.2969823 0.4246954 0.03577366 3 70 0.5677049 0.4805629 0.6607012 0.04785525
5.5. Carrier probability estimation
The carrierprob function estimates mutation carrier probabilities for relatives with missing genotype information using observed genotypes within the families condition = “geno” or alternatively, with the addition of phenotype information, using condition = “geno+pheno”. When condition = “geno”, inputs for carrierprob include two methods of estimation: method = “mendelian” uses Mendelian transmission probabilities or method = “data” uses data-driven probabilities calculated from the aggregated data for each subgroup based on relation, proband’s mutation status, mode of inheritance, disease status and disease-allele frequency in the population. When condition = “geno+pheno”, method = “model” should be used to calculate the carrier probabilities based on both observed genotype and phenotype information, where the penetrance model should be specified by fit obtained from either the penmodel or penmodelEM functions.
The carrierprob function returns a dataframe that includes the estimated carrier probabilities, named carrp.geno or carrp.pheno, appended after the last column in the family data set, indicating carrier probabilities based on observed genotypes only and those based on both observed genotypes and phenotype, respectively.
6. Illustrating examples
6.1. Penetrance estimation in presence of missing genotype data
The presence of missing genotypes is a common issue in genetic studies. The R package FamEvent can be used to generate and analyze family data with missing genotypes for the major gene. For example, we can generate families with 30% of missing genotypes, assuming a Weibull baseline function with scale and shape parameters of 0.01 and 3, βsex = 0.5 and βgene = 2. Given the parameter values in the Weibull model, the function penplot displays penetrance functions (not shown) and also returns the true penetrance values by age 70. In our situation, those are 0.868, 0.708, 0.240, and 0.153 in male carriers, female carriers, male non-carriers, and female non-carriers, respectively. For this example, set.seed(4321) was used.
R> fam <- simfam(N.fam = 300, design = “pop+”, base.dist = “Weibull”,
+ allelefreq = 0.02, base.parms = c(0.01, 3), vbeta = c(0.5, 2),
+ probandage = c(45, 2.5), agemin = 15, mrate = 0.3)
R> penplot(base.parms = c(0.01, 3), vbeta = c(0.5, 2),
+ base.dist = “Weibull”, agemin = 15)
Call: Weibull baseline
Penetrance by age 70:
male-carrier female-carrier male-noncarr female-noncarr
0.8682518 0.7075186 0.2399006 0.1532713
For model fitting in the presence of missing genotypes, we can consider two approaches: complete-case analysis and an EM algorithm as implemented in FamEvent. The complete-case approach simply ignores the missing genotypes, i.e., considers only the subset of individuals with complete information. Alternatively, the EM algorithm approach can infer missing genotypes by computing the conditional probability of being carriers given the phenotype information in the family (see Section 3.3). In FamEvent, the complete-case analysis is performed with the penmodel function and the EM algorithm with the penmodelEM function. The penetrance estimates by age 70 and their CIs and SEs for male and female carriers are obtained with penetrance function. The command lines and output are:
R> fam0 <- fam[ ! is.na(fam$mgene), ]
R> fit0 <- penmodel(Surv(time, status) ~ gender + mgene, cluster = “famID”,
+ gvar = “mgene”, parms=c(0.01, 1, 0.5, 2), data = fam0, design = “pop+”,
+ base.dist=“Weibull”)
R> summary(fit0)
Estimates:
Estimate Std. Error t value Pr(>|t|)
log(lambda) −4.6506 0.06469 −71.891 0.008855 **
log(rho) 1.0669 0.03543 30.113 0.021133 *
gender 0.4626 0.13011 3.556 0.174542
mgene 2.0634 0.15650 13.185 0.048191 *
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ‘ 1
R> penetrance(fit0, fixed = c(1,1), age = 70, CI = TRUE, MC = 100)
R> penetrance(fit0, fixed = c(0,1), age = 70, CI = TRUE, MC = 100)
Fixed covariate values: gender = 1 mgene = 1
age penentrance lower upper se
1 70 0.8545536 0.8016831 0.9027098 0.0286689
Fixed covariate values: gender = 0 mgene = 1
age penentrance lower upper se
1 70 0.7029629 0.6336492 0.7653958 0.03707987
R> fitEM <- penmodelEM(Surv(time, status) ~ gender + mgene, cluster = “famID”,
+ gvar = “mgene”, parms = c(0.01, 1, 0.5, 2), data = fam, design = “pop+”,
+ base.dist = “Weibull”, method = “mendelian”)
R> summary(fitEM)
Estimates:
Estimate Std. Error t value Pr(>|t|)
log(lambda) −4.652 0.05503 −84.532 0.007531 **
log(rho) 1.079 0.03199 33.715 0.018877 *
gender 0.384 0.11011 3.488 0.177765
mgene 2.174 0.13259 16.400 0.038770 *
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ‘ 1
R> penetrance(fitEM, fixed = c(1, 1), age = 70, CI = TRUE, MC = 100)
R> penetrance(fitEM, fixed = c(0, 1), age = 70, CI = TRUE, MC = 100)
Fixed covariate values: gender = 1 mgene = 1
age penentrance lower upper se
1 70 0.8563912 0.8168521 0.8993619 0.02294077
Fixed covariate values: gender = 0 mgene = 1
age penentrance lower upper se
1 70 0.7333461 0.6782508 0.7916241 0.03105126
The accuracy and precision of parameter and penetrance estimates for the two approaches are summarized in Table 8. The estimates obtained from these two approaches are similar since the missing genotypes were generated at random from simfam function.
Table 8:
The accuracy and precision of parameter and penetrance (%) estimates using complete case analysis and the EM algorithm for 300 POP+ simulated families with 30% missing genotypes.
| Complete case | EM algorithm | ||||
|---|---|---|---|---|---|
| Parameter | True value | Estimate | SE | Estimate | SE |
| β sex | 0.5 | 0.46 | 0.13 | 0.38 | 0.11 |
| β gene | 2.0 | 2.06 | 0.16 | 2.17 | 0.13 |
| Penetrance (%) by age 70 | |||||
| male carrier | 86.83 | 85.46 | 2.87 | 85.64 | 2.29 |
| female carrier | 70.75 | 70.30 | 3.71 | 73.33 | 3.11 |
6.2. Sample size and power calculation
Sample size calculation is a critical task when designing a new family study. In penetrance estimation studies, the goal is to collect enough families to detect a genetic relative risk associated for a known mutation or genetic variant with a specified statistical power and/or to estimate the penetrance function at a certain age in gene carriers with a certain precision. We can use our R package FamEvent to perform the sample size calculation in these two situations.
For the first situation, we can construct the Wald test statistic as
where is the estimated log hazard ratio (HR) associated with a given mutation, β0 its value under the null hypothesis (e.g., β0 = 0) and is a standard error estimate of . For the one-sided test H0 : β ≤ β0 vs. H1 : β > β0, the power of the Wald test is defined as: P (W > Z1−α) under the alternative hypothesis, where Z1−α is the (1−α)th quantile of the standard normal distribution. The power function for β > β0 can then be obtained from the asymptotic normality of the maximum likelihood estimator as
where Φ(.) the cumulative normal distribution.
We can then perform some simulations with FamEvent package to determine the number of families needed to achieve a certain power. Since β and β0 are fixed, simulating different family sizes will affect the standard error of and hence the power of the test. For example, we simulated 50 families under the POP+ design, using a Weibull baseline function with shape and scale parameters of 0.01 and 3, a gender effect with βgender = 1 (i.e., HR = 2.72), a dominant model for the major gene with allele frequency of 0.02 for the minor allele and βgene = 1 (HR = 2.72).
We obtained a robust standard error for of 0.34. If we assume β0 = 0 and a one-sided test with α = 0.05, the power of the Wald statistic to test for βgene > 0 is 89.8%.
R> fam50 <- simfam(50, design = “pop+”, variation = “none”,
+ base.dist = “Weibull”, base.parms = c(0.01, 3), vbeta = c(1, 1),
+ allelefreq = 0.02, probandage = c(45, 2.5), agemin = 20)
R> fit50 <- penmodel(Surv(time, status) ~ gender + mgene, cluster = “famID”,
+ gvar = “mgene”, parms = c(0.01, 3, 1, 1), data = fam50, design = “pop+”,
+ base.dist = “Weibull”, robust = TRUE)
R> summary(fit50)
Estimates:
Estimate Std. Error Robust SE t value Pr(>|t|)
log(lambda) −4.875 0.20437 0.21674 −22.493 0.02828 *
log(rho) 1.090 0.09317 0.08719 12.503 0.05081 .
gender 1.756 0.44694 0.46596 3.769 0.16509
mgene 1.384 0.37311 0.34382 4.025 0.15504
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ‘ 1
Empirically, we can also obtain the power for testing βgene > 0 from simulations using fampower function. Based on 100 simulations of 50 POP+ families, the power of 87% was obtained using the following code, i.e., the probability of 87% to reject the null hypothesis when the true effect size βgene = 1.
R> fampower(N.fam = 50, N.sim = 100, effectsize = 1, beta.sex = 1, side = 1, + base.dist = “Weibull”, design = “pop+”, base.parms = c(0.01, 3), + probandage = c(45, 2.5), agemin = 20) Number of families = 50 1 sided test alpha = 0.05 Effect size = 1 Power = 0.87
For the second situation, using similar code as above we can obtain the penetrance estimate in gene carriers at 70 years of age and its 95% CI. With 50 POP+ families and under the assumptions given above, the penetrance estimate at 70 years is 73.20% (SE = 8.74%) in males and 20.34 (SE = 8.82%) in females.
R> penetrance(fit50, fixed = c(1,1), age = 70, CI = TRUE, MC = 100) R> penetrance(fit50, fixed = c(0,1), age = 70, CI = TRUE, MC = 100) Fixed covariate values: gender = 1 mgene = 1 age penentrance lower upper se 1 70 0.7320258 0.5337312 0.8658422 0.08741793 Fixed covariate values: gender = 0 mgene = 1 age penentrance lower upper se 1 70 0.203384 0.09210014 0.4149234 0.08821385
If an investigator wants a standard error for the penetrance estimate to reach a maximum of 5% in both males and females, about 200 POP+ families would be needed as shown below the output from fitting the 200 simulated families.
R> penetrance(fit200, fixed=c(1,1), age=70, CI=TRUE, MC=100) R> penetrance(fit200, fixed=c(0,1), age=70, CI=TRUE, MC=100) Fixed covariate values: gender = 1 mgene = 1 age penentrance lower upper se 1 70 0.6070111 0.4905026 0.6932932 0.05064867 Fixed covariate values: gender = 0 mgene = 1 age penentrance lower upper se 1 70 0.2494493 0.1721935 0.367085 0.04612641
6.3. Optimal designs
Designing efficient studies is an important aspect of family studies. We illustrate this problem by considering a two-stage family design. Typically case patients (i.e., probands) are selected in the first stage and asked about the history of disease in their family and stratified into different categories, e.g., high-risk (High), intermediate-risk (Med) and low-risk (Low). In the second stage, case patients and their relatives are subsampled with different sampling probabilities that could depend on their risk category. For a fixed sample size, the goal is to estimate the sampling probability for each stratum that minimizes the variance of the estimate of the parameter of interest.
To construct an optimal design we therefore determine some optimal weights for each stratum and then decide the optimal sample sizes accordingly (in our case, the number of families to include into the study). The optimal weighting problem was discussed by Lindsay (1988) who obtained optimal weights in a way that maximizes the information over a class of estimating functions. Let w be the vector of weights, S the vector of component scores and U the score function based on the full likelihood. Then, the optimal weights are obtained by minimizing with respect to w,
and are given by
with E(US) = E(S2) where S2 denotes the vector whose elements are the squared elements of S and the variance Var(S) is a block matrix where the size of each block depends on the size of the stratum.
Consider the problems of determining the optimal weights for estimating: 1) the log hazard ratio measuring the effect of a mutation on a time-to-event outcome, and, 2) the penetrance of the mutation by age 70. We simulated family data corresponding to the three risk categories (High, Med, Low) assuming that High corresponds to the CLI+ design, Med to POP+ and Low to POP. We simulated 150 families from each design. To simulate the family data, we used a Weibull baseline function with shape and scale parameters of 0.01 and 3, respectively, a gender effect with βsex = 1 (HR = 2.72), a dominant model for the major gene with allele frequency of 0.02 for the minor allele, a mean and standard deviation for the proband’s age of 45 and 2.5 years, respectively, and a minimum age at onset for the disease of 20 years. We assumed βgene = 1.5, 0.8, and 0.5 for the High, Med and Low designs, respectively, and the associated penetrance as given in Table 9. The command lines to generate and fit family data are similar to the one described in Section 6.1.
Table 9:
Estimates of the log hazard ratio (HR) for mutation gene and penetrance at 70 years under different family designs with family size n = 150. The standard error of the estimates are indicated in brackets.
| Penetrance at 70 years | Penetrance at 70 years | ||
|---|---|---|---|
| Design | Log HR | in men (%) | in women (%) |
| CLI+ (High) | 1.84 (0.13) | 97.12 (0.95) | 75.63 (4.34) |
| POP+ (Med) | 0.95 (0.21) | 62.08 (5.62) | 25.08 (5.23) |
| POP (Low) | 0.46 (0.52) | 35.92 (13.73) | 14.17 (7.86) |
We are first interested in an optimal design for the log HR estimates. The variances for the log HR estimates in high-risk, intermediate-risk and low-risk families are 0.132, 0.212 and 0.522, respectively (Table 9). As the sampling probabilities are inversely proportional to these variances, if we plan to have a total sample size of n = 300 families, we need the collection of 212 high-, 75 intermediate-, and 13 low-risk families. However, if one wants to optimize the design for the penetrance estimate in males this will lead to the collection of 290 high-, 8 intermediate-, and 2 low-risk families and in females of 150 high-, 104 intermediate-, and 46 low-risk families, respectively.
6.4. Real data analysis
To analyze real data using penmodel or penmodelEM, the data should be prepared following the same data frame that the simfam function provides. The data frame should include column names famID, indID, motherID, fatherID, proband (coded 1 for proband, 0 for non-proband), gender (coded 1 for male, 0 for female), currentage, time, status (coded 1 for affected, 0 for unaffected), mgene (coded 1 for carrier, 0 for noncarrier, or NA for missing). When data includes a sampling weight, it should be named as weight in the data frame. Without this weight variable, all families will be equally weighted. In addition, agemin has to be specified by attr(data, “agemin”) = 18, for example.
The package includes data named LSfam from 32 Lynch Syndrome (LS) families identified through the Ontario Familial Colorectal Cancer Registry (OFCCR) (Cotterchio et al. 2000). Lynch Syndrome is an autosomal dominant condition caused by several DNA mismatch repair (MMR) genes, predominantly MLH1 and MSH2, that predisposes carriers to colorectal cancers.
The OFCCR used the population-based Ontario Cancer Registry to identify incident colorectal cancer (CRC) cases (probands), aged 20 – 74, diagnosed from July 1997 to July 2000. Probands were screened for any MMR gene mutations. For each proband found to carry an MMR mutation, all first- and second-degree relatives of the proband’s family were considered to be eligible for the study. The data set includes a total of 765 individuals. Excluding individuals without information on age at diagnosis or examination or disease status, n = 503 individuals are used for analysis including 32 probands and 471 relatives. The probands are all mutation carriers and of the 471 relatives, 60 are known mutation carriers, 62 are known non-carriers, and the mutation statuses of the rest are unknown. After loading the data, data(“LSfam”), summary.simfam(LSfam) and plot.simfam(LSfam) can be applied to provide a summary of the data and a graphical display of the pedigree structure for the first family, respectively. Using the LS family data, we aimed to estimate the effects of gender and mutation status on CRC risk and to provide age-specific penetrance estimates specific to gender and mutation status by taking missing genetic information into account. To begin, we specified the minimum age of onset as 18 years and used those whose age at onset or current age is greater than the minimum age into the analysis. What follows are two penetrance models fitted using baselines hazard distributions—Weibull and piecewise constant with cut points at c(30,40,50,60).
R> data(“LSfam”)
R> attr(LSfam, “agemin”) <- 18
R> fitLS.Weibull <- penmodelEM(Surv(time, status) ~ gender + mgene,
+ design = “pop+”, cluster = “famID”, gvar = “mgene”,
+ parms = c(0.05, 2, 1, 3), base.dist = “Weibull”, method = “mendelian”,
+ data = LSfam[ ! is.na(LSfam$time), ])
R> summary(fitLS.Weibull)
Estimates:
Estimate Std. Error t value Pr(>|t|)
log(lambda) −4.7159 0.10741 −43.906 0.01450 *
log(rho) 1.0455 0.07044 14.843 0.04283 *
gender 0.4518 0.21070 2.144 0.27779
mgene 2.3436 0.27743 8.447 0.07501.
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ‘ 1
R> plot(fitLS.Weibull, add.KM = FALSE, conf.int = TRUE, ylim = c(0, 1),
+ print = FALSE)
R> penetrance(fitLS.Weibull, fixed = c(1, 1), age = 70, CI = TRUE, MC = 100)
R> penetrance(fitLS.Weibull, fixed = c(0, 1), age = 70, CI = TRUE, MC = 100)
Fixed covariate values: gender = 1 mgene = 1
age penentrance lower upper se
1 70 0.8441975 0.7643877 0.9244254 0.04455421
Fixed covariate values: gender = 0 mgene = 1
age penentrance lower upper se
1 70 0.6937294 0.6034767 0.8011827 0.05491901
Based on the penetrance model with a Weibull baseline hazard distribution, the penetrance estimates by age 70 for male and female carriers are 84.42% (95% CI = (76.44, 92.44)%) and 69.37% (95% CI = (60.35, 80.12)%), respectively.
What follows is the penetrance model fitted with a piecewise-constant baseline. Although it provides more flexibility, it takes longer time to converge as it uses more parameters to estimate the baseline hazard. The penetrance estimates by age 70 for male and female carriers are 80.47% (95% CI = (70.37, 90.59)%) and 67.22% (95% CI = (58.89, 78.04)%), respectively, which are slightly lower compared to the Weibull baseline hazards model. The AIC values for these models are 1111 and 1149, respectively obtained from fitLS.Weibull$AIC and fitLS.piece$AIC.
R> fitLS.piece <- penmodelEM(Surv(time, status) ~ gender + mgene,
+ design = “pop+”, cluster = “famID”, gvar = “mgene”,
+ base.dist = “piecewise”, parms = c(rep(0.01, 5), 1, 1.5),
+ cuts = c(30, 40, 50, 60), method = “mendelian”,
+ data = LSfam[ ! is.na(LSfam$time), ] )
R> summary(fitLS.piece)
Estimates:
Estimate Std. Error t value Pr(>|t|)
log(q1) −8.1065 0.4346 −18.654 0.03409 *
log(q2) −7.0434 0.3649 −19.304 0.03295 *
log(q3) −5.8203 0.3141 −18.530 0.03432 *
log(q4) −5.4490 0.3118 −17.474 0.03639 *
log(q5) −4.9240 0.2801 −17.578 0.03618 *
gender 0.3815 0.2110 1.808 0.32163
mgene 1.9561 0.2581 7.580 0.08351 .
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ‘ 1
R> plot(fitLS.piece, add.KM = FALSE, conf.int = TRUE, ylim = c(0,1),
+ print = FALSE)
R> penetrance(fitLS.piece, fixed = c(1, 1), age = 70, CI = TRUE, MC = 100)
R> penetrance(fitLS.piece, fixed = c(0, 1), age = 70, CI = TRUE, MC = 100)
Fixed covariate values: gender = 1 mgene = 1
age penentrance lower upper se
1 70 0.804729 0.7036892 0.9059321 0.05401238
Fixed covariate values: gender = 0 mgene = 1
age penentrance lower upper se
1 70 0.672183 0.588948 0.780449 0.05204197
Figure 3 displays the penetrance curves ranging from 20 to 80 years for four groups specific to gender and mutation status based on the Weibull (left panel) and piecewise constant (right panel) baselines.
Figure 3:
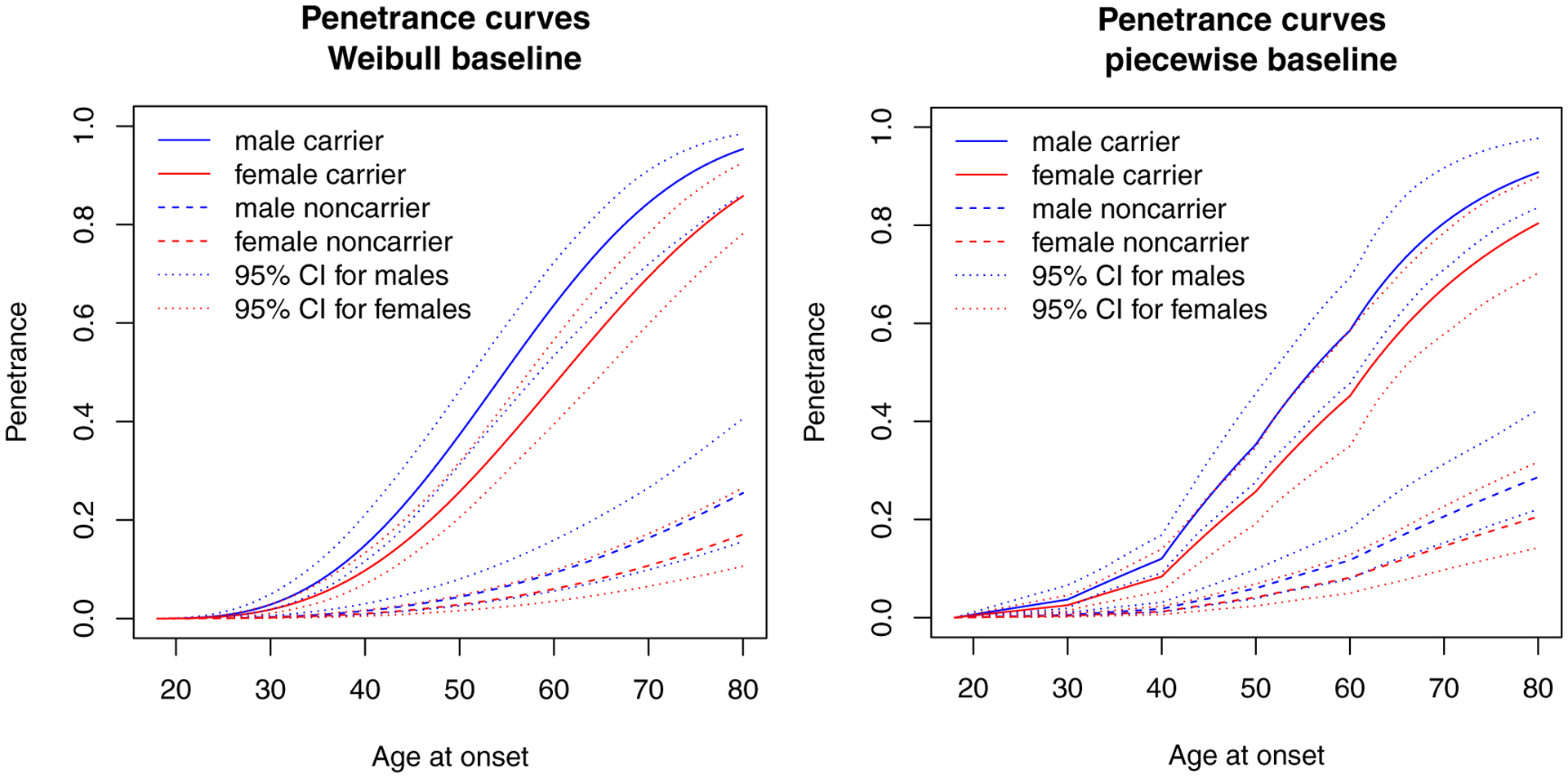
Penetrance functions estimated using Weibull (left) and piecewise constant (right) baselines for Lynch Syndrome families recruited from the OFCCR.
7. Conclusions
FamEvent is a comprehensive R package for simulating and modelling time-to-event data from family-based study designs. Family-based designs continue to be powerful approaches to study complex diseases with a genetic basis, even with increasingly low costs for whole genome sequencing. For example, a recent consortium for affective and psychotic disorders has been developed to identify genetic factors for mental illness (Glahn et al. 2019). Genetic factors are being identified from family studies in vastly different diseases, disorders and behaviours including the intergenerational transmission of divorce (Salvatore et al. 2018), Alzheimer’s Disease (Beecham et al. 2017), human longevity (Yashin et al. 2018), and the impact of the rearing environment on children’s behaviour (Liu and Neiderhiser 2017).
Common issues encountered in family-based designs, regardless of the research domain, include missing genotype information on family members, selection of the families and residual correlation after conditioning on the major gene. Substantial bias in penetrance parameter estimates as well as underestimation of variability can occur without addressing these issues in the analysis of data. No existing R packages, such as gap, pbatR, or coxme, address the missing genotype information or selection bias in their methods. FamEvent is a versatile and user-friendly R package for simulating and fitting time-to-event data in complex pedigrees under various sampling designs. It assumes the segregation of a major gene with or without the presence of residual correlation due to a second gene or shared frailty. The simulated data can mimic real data obtained in many types of family studies. Mutation carrier probabilities for individuals with missing genotypes can also be estimated using information on the relatives’ genotypes and possibly phenotypes using the carrierprob function in the FamEvent package.
Plotting functions permit visual examination of individual pedigrees, as well as the true and estimated penetrance functions while several summary and print options provide the key parameter and penetrance estimates from fitted models or details of the simulated family data set. The power of detecting a genetic effect in the penetrance model based on a family-based simulation study is available in the fampower function. The FamEvent R package also includes data from 32 Lynch Syndrome families segregating MMR mutations selected from the Ontario Familial Colorectal Cancer Registry, including 765 relatives; these data will permit other users to evaluate their models or methods. This package addresses important features of age-at-onset data from common family-based designs, generates data that mimics real family data, and provides important tools for investigators planning family-based studies or analyzing their corresponding data.
Future extensions will include more sophisticated functions for penetrance estimation as well as the simulation of time-to-event data in the context of familial sequencing studies. For instance, we have started to use FamEvent in combination with our other R package sim1000G (Dimitromanolakis et al. 2019), which simulates genetic variants according to the 1000 Genomes data. The penetrance function can then depend on a multi-allelic genetic marker, where the marker can be composed of rare or common genetic variants or a combination of both. This is particularly useful to simulate a pattern of familial aggregation of age-at-onset outcomes given a complex genetic architecture. For example, we recently used FamEvent to simulate a familial aggregation of age at colorectal cancer onset in Familial Colorectal Cancer Type X families to investigate the type of genetic architecture that could explain this familial aggregation (Choi et al. 2019b). FamEvent was also used in combination with sim1000G to assess the power of rare variant association tests in family designs for time-to-event data (Dimitromanolakis et al. 2019) and to simulate sister pair data under early age at onset ascertainment, where the genetic model reflects a scientific hypothesis of locus heterogeneity (Romanescu et al. 2018). This demonstrates that FamEvent can have a broad range of applications in complex genomic studies and we anticipate more to come. This will motivate our future extensions of FamEvent.
Acknowledgements
This research was supported by two grants from the Canadian Institutes of Health Research (MOP 126186 & 110053), an Interdisciplinary Health Research Team award from the Canadian Institutes of Health Research (Grant # 43821), a grant from the Canadian Breast Cancer Foundation (BC-RG-15-2 competition), and Discovery Grants from the Natural Sciences and Engineering Research Council of Canada.
Contributor Information
Yun-Hee Choi, The University of Western Ontario.
Laurent Briollais, Lunenfeld-Tanenbaum Research Institute University of Toronto.
Wenqing He, The University of Western Ontario.
Karen Kopciuk, University of Calgary, Alberta Health Services.
References
- Beecham GW, Bis J, Martin E, Choi SH, DeStefano AL, van Duijn C, Fornage M, Gabriel S, Koboldt D, Larson D, Naj A, Psaty B, Salerno W, Bush W, Foroud T, Wijsman E, Farrer L, Goate A, Haines J, Pericak-Vance MA, Boerwinkle E, Mayeux R, Seshadri S, Schellenberg G (2017). “The Alzheimer’s Disease Sequencing Project: Study Design and Sample Selection.” Neurology Genetics, 3(5). doi: 10.1212/NXG.0000000000000194. URL https://ng.neurology.org/content/3/5/e194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boehnke M (1986). “Estimating the Power of a Proposed Linkage Study: A Practical Computer Simulation Approach.” American Journal of Human Genetics, 39(4), 513–527. [PMC free article] [PubMed] [Google Scholar]
- Choi YH, Briollais L (2011). “An EM Composite Likelihood Approach for Multistage Sampling of Family Data.” Statistical Sinica, 21, 231–253. [PMC free article] [PubMed] [Google Scholar]
- Choi YH, Kopciuk K, He W, Briollais L (2019a). FamEvent: Family Age-at-Onset Data Simulation and Penetrance Estimation. R package version 2.0, URL https://cran.r-project.org/package=FamEvent.
- Choi YH, Kopciuk KA, Briollais L (2008). “Estimating Disease Risk Associated with Mutated Genes in Family-Based Designs.” Human Heredity, 66, 238–251. [DOI] [PubMed] [Google Scholar]
- Choi YH, Lakhal-Chaieb L, Król A, Yu B, Buchanan D, Ahnen D, Le Marchand L, Newcomb PA, Win AK, Jenkins M, Lindor NM, Briollais L (2019b). “Comparison of Risks of Colorectal Cancer and Cancer-related Mortality in Familial Colorectal Cancer Type X and Lynch Syndrome Families.” Journal of the National Cancer Institute, 111(7), 675–683. URL 10.1093/jnci/djy159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cotterchio M, McKeown-Eyssen G, Sutherland H, Buchan G, Aronson M, Easson AM, Macey J, Holowaty E, Gallinger S (2000). “Ontario Familial Colon Cancer Registry: Methods and First Year Response Rates.” Chronic Diseases in Canada, 21, 81–86. [PubMed] [Google Scholar]
- Dimitromanolakis A, Xu J, Król A, Briollais L (2019). “sim1000G: A User-friendly Genetic Variant Simulator in R for Unrelated Individuals and Family-based Designs.” BMC Bioinformatics, 20(1), 26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fay MP, Graubard BI (2001). “Small Sample Adjustments for Wald-type Tests using Sandwich Estimators.” Biometrics, 57(4), 1198–1206. [DOI] [PubMed] [Google Scholar]
- Glahn DC, Nimgaonkar VL, Raventós H, Contreras J, McIntosh AM, Thomson PA, Jablensky A, McCarthy NS, Charlesworth JC, Blackburn NB, et al. (2019). “Rediscovering the Value of Families for Psychiatric Genetics Research.” Molecular Psychiatry, 24(4), 523–535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoffmann T, with contributions fromLange Christoph (2018). pbatR: Pedigree/Family-Based Genetic Association Tests Analysis and Power. R package version 2.2–13, URL https://CRAN.R-project.org/package=pbatR.
- Imbens GW, Kolesár M (2016). “Robust Standard Errors in Small Samples: Some Practical Advice.” Review of Economics and Statistics, 98(4), 701–712. [Google Scholar]
- Kopciuk KA, Choi YH, Parkhomenko E, Parfrey P, McLaughlin JR, Green J, Briollais L (2009). “Penetrance of HNPCC-related Cancers in a Retrospective Cohort of 12 Large Newfoundland Families Carrying a MSH2 Founder Mutation: An Evaluation using Modified Segregation Models in HNPCC Families.” Hereditary Cancer in Clinical Practice, 7(16). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lange C, Laird NM (2002). “Power Calculations for a General Class of Family-based Association Tests: Dichotomous Traits.” American Journal of Human Genetics, 67, 575–584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lawless JF (2003). Statistical Models and Methods for Lifetime Data, 2nd edition. New Jersey: John Wiley and Sons. [Google Scholar]
- Lawless JF, Kalbfleisch JD, Wild CJ (1999). “Semiparametric Methods for Response Selective and Missing Data Problems in Regression.” Journal of the Royal Statistical Society, Series B, 61, 413–438. [Google Scholar]
- Leal SM, Yan K, Müller-Myhsok B (2005). “SimPed: A Simulation Program to Generate Haplotype and Genotype Data for Pedigree Structures.” Human Heredity, 60(2), 119–122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu C, Neiderhiser JM (2017). “Using Genetically Informed Designs to Understand the Environment: The Importance of Family-Based Approaches.” In Gene-Environment Transactions in Developmental Psychopathology, pp. 95–110. Springer-Verlag. [Google Scholar]
- R Development Core Team (2019). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. URL https://www.R-project.org/. [Google Scholar]
- Romanescu RG, Gos G, Andrulis IL, Bull SB (2018). “Rare Variant Tests for Association in Affected Sib Pairs.” Genetic Epidemiology, 42(7), 728. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salvatore JE, Larsson Lönn S, Sundquist J, Sundquist K, Kendler KS (2018). “Genetics, the Rearing Environment, and the Intergenerational Transmission of Divorce: A Swedish National Adoption Study.” Psychological Science, 29(3), 370–378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmidt M, Hauser ER, Martin ER, Schmidt S (2005). “Extension of the SIMLA Package for Generating Pedigrees with Complex Inheritance Patterns: Environmental Covariates, Gene-gene and Gene-environment Interaction.” Statistical Applications in Genetics and Molecular Biology, 4(1), Article15. URL 10.2202/1544-6115.1133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shawky RM (2014). “Reduced Penetrance in Human Inherited Disease.” Egyptian Journal of Medical Human Genetics, 15(2), 103–111. [Google Scholar]
- Sinnwell J, Therneau T (2019). kinship2: Pedigree Functions. R package version 1.8.4, URL https://CRAN.R-project.org/package=kinship2.
- The Comprehensive R Archive Network (2019). The Comprehensive R Archive Network (CRAN). Wirtschaftsuniversität Wien, Vienna, Austria. URL https://cran.r-project.org/. [Google Scholar]
- Therneau TM (2015). survival: A Package for Survival Analysis in S. R package 2.38, URL https://CRAN.R-project.org/package=survival.
- Therneau TM (2019). coxme: Mixed Effects Cox Models. R package version 2.2–14, URL https://CRAN.R-project.org/package=coxme.
- White H (1982). “Maximum Likelihood Estimation of Misspecified Models.” Econometrica, 50, 1–25. [Google Scholar]
- Wijsman EM (2005). Penetrance, Encyclopedia of Biostatistics. New York: John Wiley and Sons. [Google Scholar]
- Yashin AI, Arbeev KG, Wu D, Arbeeva LS, Bagley O, Stallard E, Kulminski AM, Akushevich I, Fang F, Wojczynski MK, et al. (2018). “Genetics of Human Longevity from Incomplete Data: New Findings from the Long Life Family Study.” The Journals of Gerontology: Series A, 73(11), 1472–1481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao JH (2007). “gap: Genetic Analysis Package.” Journal of Statistical Software, 23(8), 1–18. URL http://www.jstatsoft.org/v23/i08. [Google Scholar]
- Zhao JH (2019). gap: Genetic Analysis Package. R package version 1.2.1, URL https://CRAN.R-project.org/package=gap. [Google Scholar]


