Abstract
Background
Meta-analysis is increasingly used to synthesize proportions (e.g., disease prevalence). It can be implemented with widely used two-step methods or one-step methods, such as generalized linear mixed models (GLMMs). Existing simulation studies have shown that GLMMs outperform the two-step methods in some settings. It is, however, unclear whether these simulation settings are common in the real world. We aim to compare the real-world performance of various meta-analysis methods for synthesizing proportions.
Methods
We extracted datasets of proportions from the Cochrane Library and applied 12 two-step and one-step methods to each dataset. We used Spearman’s ρ and the Bland–Altman plot to assess their results’ correlation and agreement. The GLMM with the logit link was chosen as the reference method. We calculated the absolute difference and fold change (ratio of estimates) of the overall proportion estimates produced by each method vs. the reference method.
Results
We obtained a total of 43,644 datasets. The various methods generally had high correlations (ρ > 0.9) and agreements. GLMMs had computational issues more frequently than the two-step methods. However, the two-step methods generally produced large absolute differences from the GLMM with the logit link for small total sample sizes (< 50) and crude event rates within 10–20% and 90–95%, and large fold changes for small total event counts (< 10) and low crude event rates (< 20%).
Conclusions
Although different methods produced similar overall proportion estimates in most datasets, one-step methods should be considered in the presence of small total event counts or sample sizes and very low or high event rates.
Supplementary Information
The online version contains supplementary material available at 10.1007/s11606-021-07098-5.
KEY WORDS: Cochrane review, data transformation, generalized linear mixed model, meta-analysis, proportion
INTRODUCTION
Epidemiological and medical studies frequently report proportions, including the prevalence of disease, case fatality rate, and sensitivity and specificity of a diagnostic test.1,2 Meta-analysis approaches have been increasingly used to synthesize proportion estimates from multiple studies on common topics over the past decade.3 Various methods are available for this purpose, and we may group them into two classes. The first class includes the two-step methods that are widely used in current practice. Because conventional meta-analysis models assume the input data are normally distributed,4 proportion estimates from individual studies are first transformed using a certain function to approximately meet this assumption. Meta-analyses are subsequently performed on the transformed scale, and the synthesized results are back-transformed to the proportion scale from 0 to 100% at the final step.5 Among many options, the Freeman–Tukey double-arcsine transformation has been popular in contemporary meta-analyses of proportions3,6 because it has the advantages of stabilizing variances of transformed proportions and producing smaller biases compared with other transformations.5,7 For example, it was used in a recent systematic review to pool the prevalence of COVID-19 among pregnant women.8 Nevertheless, this transformation suffers from several limitations, such as lacking intuitive interpretations and the potential to give misleading conclusions.9–11
The second class of methods includes generalized linear mixed models (GLMMs).12–15 Although they are less frequently used in current practice, existing simulation studies have shown that these methods outperform the two-step methods in several settings.16,17 They do not require data transformations within studies and thus are referred to as one-step methods. They fully account for uncertainties and thus produce confidence intervals (CIs) with satisfactory coverage probabilities.18 They can be feasibly implemented via many statistical software programs, including SAS and several R packages.17
In a recent survey of 152 meta-analyses of prevalence investigated by Borges Migliavaca et al.,3 32 (21.1%) applied the Freeman–Tukey double-arcsine transformation, 5 (3.3%) applied the logit transformation, and 4 (2.6%) applied the log transformation, while 107 (70.4%) did not explicitly specify the transformations. Although several existing simulation studies have compared the various methods,5,9,16,17 the performance of these methods depends heavily on how the meta-analysis data are simulated. It is largely unclear whether the simulation settings are representative of real-world meta-analyses of proportions. The one-step methods generally perform better than the two-step methods in cases of rare events or small sample sizes, while the two types of methods produce similar results in cases of common events and sufficiently large sample sizes.19,20 Nevertheless, there is no consensus on cutoffs for distinguishing small vs. large sample sizes, rare vs. common events, etc. In addition, the methods’ performance also depends on the number of studies and the extent of heterogeneity. It is infeasible to match real-world settings with existing knowledge from simulation studies and determine the appropriate methods for a specific meta-analysis. This article fills this research gap. We use a large collection of meta-analysis datasets published in the Cochrane Library to evaluate the differences between the overall proportion estimates produced by the various meta-analysis methods.
METHODS
Data Sources
We iteratively downloaded all data of each systematic review published in the Cochrane Database of Systematic Reviews from 2003 Issue 1 to 2020 Issue 1. Each Cochrane review dealt with a specific healthcare-related topic. Some reviews had multiple updates during this period; we only included their latest versions. Moreover, we excluded data from withdrawn reviews.
Each Cochrane review may contain multiple meta-analyses on different outcomes, intervention comparisons, or subgroups. We extracted meta-analyses of intervention comparisons with binary outcomes, and we focused on their control groups to investigate the performance of meta-analysis methods for synthesizing proportions. The control group in each meta-analysis contributed a dataset of proportions. Our analyses were restricted to the datasets with at least three studies.21
Synthesis of Proportions
We applied both the two-step and one-step meta-analysis methods to each dataset of proportions. Appendix A in the Supplemental Information gives a brief review of these methods. For the two-step methods, we used the log, logit, arcsine-square-root, and Freeman–Tukey double-arcsine transformations. For the Freeman–Tukey double-arcsine transformation, a sample size is required for back-transforming the synthesized result to the original proportion scale,10 while this sample size is not well defined for the synthesized result (Appendix A). As suggested by several researchers,5,10,11,17 we considered the harmonic, geometric, and arithmetic means of study-specific sample sizes, as well as the inverse of the variance of the synthesized result. These led to seven two-step methods in total.
When applying the one-step methods, we considered the GLMMs with the commonly used log, logit, probit, cauchit, and complementary log-log (cloglog) link functions, leading to five one-step methods in total. The GLMMs with the log and logit links correspond to the two-step methods with the log and logit transformations, respectively, but the GLMMs fully account for within-study uncertainties. The probit, cauchit, and cloglog links do not correspond to commonly used transformations for the two-step methods. Similarly, the arcsine-based transformations for the two-step methods do not correspond to well-known links for GLMMs. The different links used in GLMMs essentially correspond to different distributional assumptions for continuous latent variables (e.g., Hospital Anxiety and Depression Scale score) that are dichotomized to produce the binary data (e.g., depression).2,22 For example, the logit and probit links correspond to the logistic and normal distributions of continuous latent variables, respectively. The cauchit link corresponds to the Cauchy distribution, which is suitable for modeling data with extreme values. The cloglog link corresponds to an asymmetric distribution (specifically, the so-called extreme value distribution), and it may be suitable for modeling skewed data.
Implementations
We estimated the overall proportion in each dataset via the maximum-likelihood (ML) approach using both the two-step and one-step methods. All meta-analyses were performed under the random-effects setting to account for heterogeneity between studies. Of note, although the restricted maximum-likelihood (REML) estimators may be superior to the ML estimators,23 GLMMs are usually implemented via the ML approach because the REML estimation for GLMMs is computationally challenging.24 Our analyses were performed in R (version 4.0.2) with package “altmeta” (version 3.2). We obtained the overall proportion estimate and its 95% confidence interval (CI) in each meta-analysis. We recorded when the implementations of GLMMs failed (specifically due to the convergence issues related to maximizing likelihood algorithms).
Comparisons of Various Methods
Existing simulation studies have shown that the one-step GLMMs generally produce smaller biases and mean squared errors and CIs with higher coverage probabilities than the two-step methods.16,17 In addition, the logit link is the canonical link for binomial data, and proportions on the logit scale have intuitive interpretations (i.e., log odds) for practitioners. Therefore, we chose the GLMM with the logit link as the reference method when comparing the various methods. We visualized the estimated overall proportions produced by each method against those by the reference method, and we calculated Spearman’s rank correlation coefficient ρ to assess their correlation. Similar analyses were repeated for the lower and upper bounds of 95% CIs.
Moreover, we calculated the absolute difference of the estimated overall proportions produced by each method and the reference method for each dataset. Since proportions are bounded at 0%, outcomes with rare events are likely to have smaller differences. In addition to the absolute difference, we also calculated the fold change of the estimated overall proportion by each method vs. the reference method. The fold change is defined as the ratio of a larger estimate divided by a smaller estimate; thus, it has a minimum value of 1.25 For example, 55% and 50% had an absolute difference of 5% and a fold change of 1.1; 0.2% and 0.1% had a much smaller absolute difference of 0.1% but a much larger fold change of 2. The interpretations of the fold change’s extent may differ case by case, depending on the importance of outcomes, etc.; roughly, a fold change > 1.2 may be considered large.25,26
For each method, we additionally investigated how the computational failures, Spearman’s rank correlation coefficients, absolute differences, and fold changes were related to (1) the number of studies, (2) the total event count, (3) the total sample size, and (4) the crude event rate within a meta-analysis. The crude event rate was calculated as the total event count divided by the total sample size. The total sample size was categorized based on the cutoffs of 10 to 200 by increments of 10. The crude event rate was categorized based on the cutoffs of 0.1%, 0.5%, 1%, 5%, 10% to 90%, 95%, 99%, 99.5%, and 99.9%.
For the one-step GLMMs, we also obtained the value of the Akaike information criterion (AIC) for each dataset. The AIC is a tool for model selection, with smaller values indicating better models. We calculated the difference in AIC between each GLMM and the reference method; a negative difference implied that the corresponding GLMM performed better than the reference method. A difference > 5 (in absolute magnitude) in AIC may be considered substantial.27
RESULTS
Basic Characteristics
In total, we obtained 43,644 datasets of proportions from 3244 Cochrane reviews. Table S1 summarizes some descriptive statistics about the datasets. Most meta-analyses contained few studies, with a median of 5. The median of total event counts was 56 (interquartile range [IQR], 18 to 163), and 1063 (2.4%) meta-analyses had zero total event counts. The total sample sizes had a median of 438 (IQR, 200 to 1049), and the crude event rates had a median of 12.6% (IQR, 4.4 to 29.8%). Tables S2–S5 give the counts of datasets in categories based on the number of studies, total event count, total sample size, and crude event rate.
Computational Issues
Table 1 presents the counts and proportions of datasets that led to computational issues when using the various methods. In the presence of such issues, the methods failed to produce synthesized proportion estimates. All two-step methods led to computational issues in < 1% of the datasets, while the log transformation had more computational issues than other transformations. The one-step GLMMs produced computational issues more frequently than the two-step methods. The GLMM with the logit link generally produced fewer issues than other one-step methods, but its proportion of computational issues (6.3%) was still higher than that of the two-step methods. The GLMM with the cauchit link produced more computational issues than the GLMMs with the probit and cloglog links.
Table 1.
Results Produced by the Various Methods for Synthesizing Proportions Among Cochrane Datasets (n = 43,644)
| Method | Failure* | Absolute difference† | Fold change† |
|---|---|---|---|
| Two-step (log) | 260 (0.6%) | 0.9% (0.2%, 2.4%) | 1.10 (1.03, 1.46) |
| Two-step (logit) | 215 (0.5%) | 0.6% (0.2%, 1.8%) | 1.07 (1.02, 1.42) |
| Two-step (arcsine) | 113 (0.3%) | 0.4% (0.0%, 1.3%) | 1.05 (1.01, 1.26) |
| Two-step (DAS-H) | 125 (0.3%) | 0.3% (−0.1%, 1.2%) | 1.06 (1.01, 1.25) |
| Two-step (DAS-G) | 125 (0.3%) | 0.4% (−0.1%, 1.4%) | 1.06 (1.01, 1.26) |
| Two-step (DAS-A) | 125 (0.3%) | 0.5% (0.0%, 1.5%) | 1.06 (1.01, 1.30) |
| Two-step (DAS-IV) | 125 (0.3%) | 0.6% (0.1%, 1.6%) | 1.06 (1.01, 1.36) |
| GLMM (log) | 3822 (8.8%) | 0.0% (−0.4%, 0.0%) | 1.01 (1.00, 1.03) |
| GLMM (probit) | 2766 (6.3%) | 0.0% (0.0%, 0.2%) | 1.00 (1.00, 1.02) |
| GLMM (cauchit) | 5708 (13.1%) | 0.0% (−0.5%, 0.0%) | 1.02 (1.00, 1.10) |
| GLMM (cloglog) | 2818 (6.5%) | 0.0% (−0.2%, 0.0%) | 1.00 (1.00, 1.01) |
| GLMM (logit) | 2131 (4.9%) | Reference | Reference |
*The column of “failure” gives the counts of datasets that led to computational issues when using the various methods. The corresponding proportions are given in parentheses
†The columns of “absolute difference” and “fold change” give the medians of absolute differences and fold changes of the overall proportion estimates produced by the various methods compared with the reference method. The corresponding interquartile ranges are given in parentheses. The fold change is the ratio of a larger estimate of the overall proportion divided by a smaller estimate
Abbreviations: Two-step (log, logit, or arcsine), two-step method with the log, logit, or arcsine-square-root transformation; Two-step (DAS-H, DAS-G, DAS-A, or DAS-IV), two-step method with the Freeman–Tukey double-arcsine (DAS) transformation, using the harmonic (H), geometric (G), or arithmetic (A) mean of study-specific sample sizes, or using the inverse of the variance (IV) of the synthesized result, as the overall sample size; GLMM (log, logit, probit, cauchit, or cloglog), generalized linear mixed model with the log, logit, probit, cauchit, or complementary log-log link
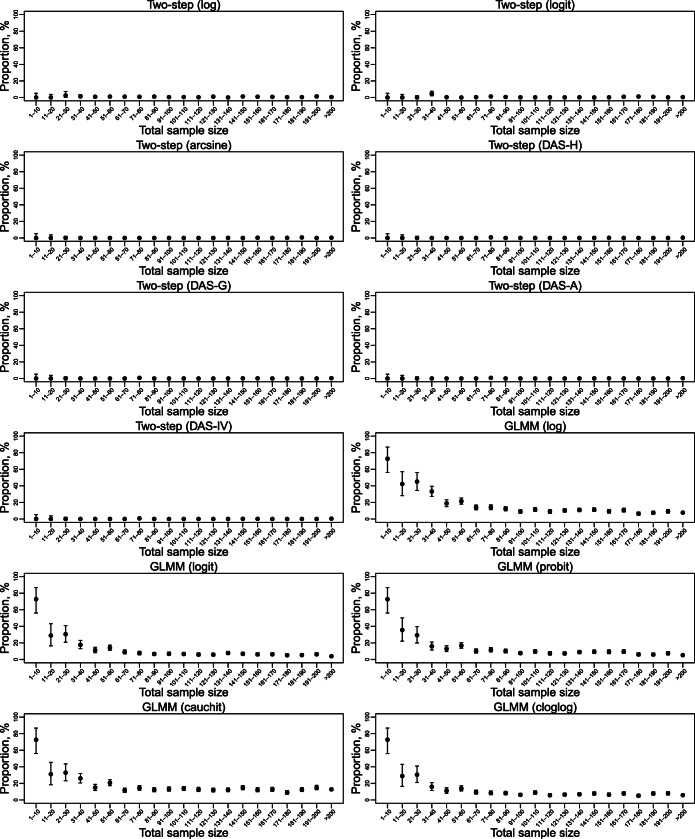
Figures 1 and S1–S4 illustrate how the number of studies, total event count, total sample size, and crude event rate affected computational issues. Because the two-step methods had fewer computational issues than the one-step GLMMs, the following interpretations focus on the GLMMs. The GLMMs could not be implemented in all meta-analyses with zero total event counts. Excluding such meta-analyses, the proportion of computational issues seemed to slightly increase as the number of studies or the total event count increased (Figs. S1–S3). For the GLMM with the cauchit link, the proportion of computational issues was relatively high across different settings. Figure 1 shows that the proportion of computational issues decreased as the total sample size increased. In addition, the GLMMs very likely had computational issues when the crude event rate was < 0.1% or > 99.9% (Fig. S4). The proportion of computational issues produced by the GLMM with the log link sharply increased as the crude event rate increased, especially when the crude event rate was > 50%.
Figure 1.
Proportions (with 95% confidence intervals) of Cochrane datasets that led to computational issues when using various meta-analysis methods, categorized by the total sample size within a meta-analysis. The two-step method (DAS-H, DAS-G, DAS-A, or DAS-IV) corresponds to the Freeman–Tukey double-arcsine (DAS) transformation, using the harmonic (H), geometric (G), or arithmetic (A) mean of study-specific sample sizes, or using the inverse of the variance (IV) of the synthesized result, as the overall sample size.
Comparisons of Results from the 12 Meta-analysis Methods
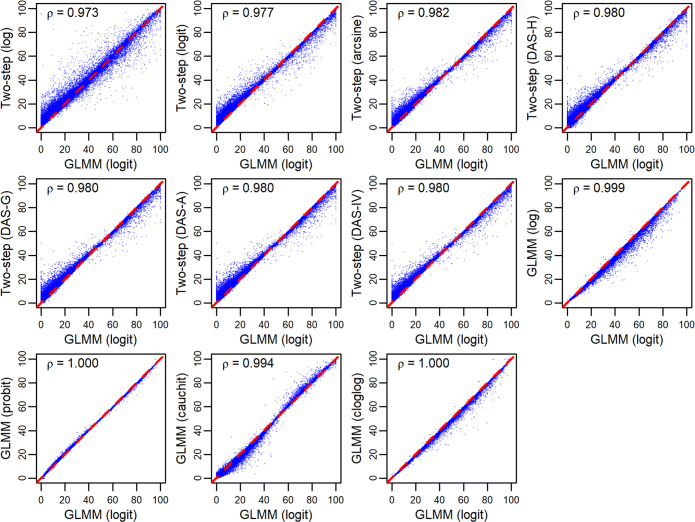
Figure 2 presents the overall proportion estimates produced by the various methods against the reference method, and Figure 3 presents the associated Bland–Altman plots. The figures and the following results were based on the datasets whose overall proportions were successfully produced by both methods in each pairwise comparison without computational issues. Spearman’s ρ was > 0.97 for each pairwise comparison. The various methods produced very similar results with median absolute differences close to 0% and median fold changes close to 1 (Table 1). The GLMMs with different links produced nearly identical results, with ρ>0.99. The GLMM with the probit link seemed to have the most similar performance to the reference method of the GLMM with the logit link. Despite the high correlations, the overall proportion estimates in some meta-analyses by different methods were noticeably different. For example, the two-step method with the logit transformation tended to produce larger and smaller overall proportion estimates than the GLMM with the logit link when the overall proportions were close to 0% and 100%, respectively.
Figure 2.
Scatter plots of overall proportion estimates (in percentage) produced by various meta-analysis methods against those by the generalized linear mixed model with the logit link among Cochrane datasets. In each panel, the diagonal dashed line represents the identity line, and Spearman’s rank correlation coefficient ρ between the corresponding two meta-analysis methods is displayed. The two-step method (DAS-H, DAS-G, DAS-A, or DAS-IV) corresponds to the Freeman–Tukey double-arcsine (DAS) transformation, using the harmonic (H), geometric (G), or arithmetic (A) mean of study-specific sample sizes, or using the inverse of the variance (IV) of the synthesized result, as the overall sample size.
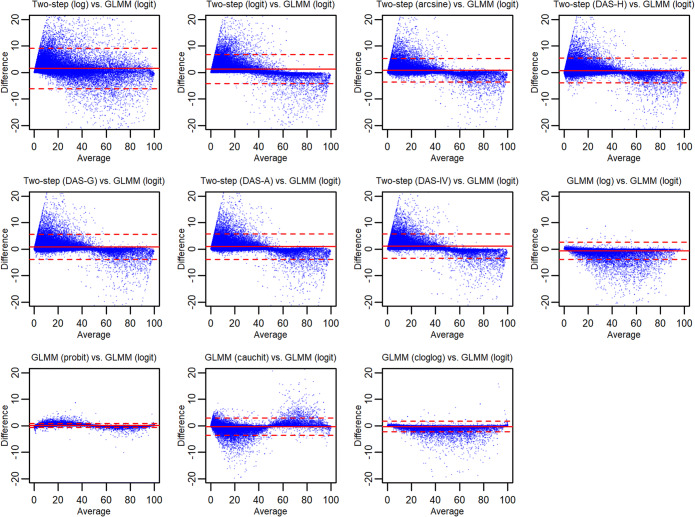
Figure 3.
Bland–Altman plots of agreement between overall proportion estimates (in percentage) produced by various meta-analysis methods and those by the generalized linear mixed model with the logit link among Cochrane datasets. In each panel, the horizontal solid line represents the mean difference, and the horizontal dashed lines represent 95% limits of agreement. The two-step method (DAS-H, DAS-G, DAS-A, or DAS-IV) corresponds to the Freeman–Tukey double-arcsine (DAS) transformation, using the harmonic (H), geometric (G), or arithmetic (A) mean of study-specific sample sizes, or using the inverse of the variance (IV) of the synthesized result, as the overall sample size.
Figures S5–S8 show the relationships between Spearman’s ρ and the number of studies, total event count, total sample size, and crude event rate. Spearman’s ρ for GLMMs was generally high across different settings. The number of studies had a small impact on Spearman’s ρ for the two-step methods (Fig. S5). Spearman’s ρ could be noticeably lower for smaller total event counts (Fig. S6). For crude event rates close to 0% or 100%, Spearman’s ρ could be as low as 0.2 (Fig. S8).
Figures S9 and S10 present the lower and upper bounds of 95% CIs, respectively, and Figures S11 and S12 present the corresponding Bland–Altman plots. The correlations were smaller than those for the point estimates. The two-step methods tended to produce larger CI lower bounds and smaller CI upper bounds than the reference method. The GLMM with the cauchit link generally produced larger CI upper bounds than the reference method, with ρ < 0.7.
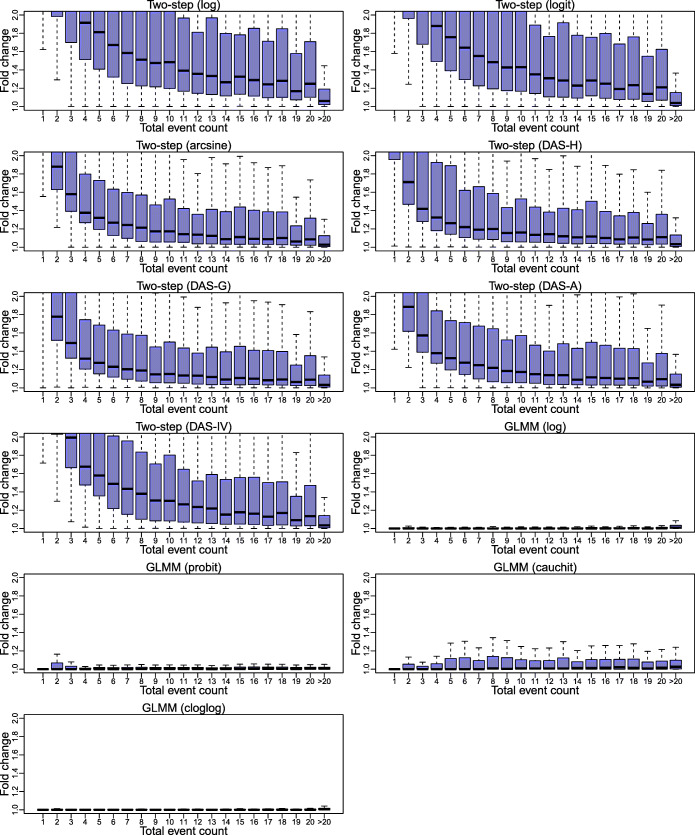
Figures S13 and S17 present the histograms of absolute differences and fold changes by the various methods. Consistent with Figure 2, absolute differences and fold changes were close to 0 and 1 for GLMMs, respectively, while absolute differences could be > 6% and fold changes could be > 2 for the two-step methods in a considerable number of datasets. Because the absolute differences and fold changes among GLMMs were mostly tiny, we focus on those for the two-step methods in the following. The absolute difference and fold change slightly increased as the number of studies increased (Figs. S14 and S18). As the total event count increased, the absolute difference slightly decreased toward 0 (Fig. S15), while the fold change dramatically decreased toward 1 (Fig. 4). As the total sample size increased, the absolute difference dramatically decreased (Fig. 5), while the fold change did not change much (Fig. S19). When the crude event rate was < 50%, the absolute difference tended to be positive, and they mostly changed to be negative when the crude event rate was >50% (Fig. S16). The fold change sharply decreased toward 1 when the crude event rate increased from 0 to 20% (Fig. S20).
Figure 4.
Box plots of fold changes of overall proportion estimates produced by various meta-analysis methods compared with those by the generalized linear mixed model with the logit link among Cochrane datasets, categorized by the total event count within a meta-analysis. Because many datasets led to extreme values of fold changes, the box plots do not present outliers, and the vertical axis only presents the range from 1 to 2. The two-step method (DAS-H, DAS-G, DAS-A, or DAS-IV) corresponds to the Freeman–Tukey double-arcsine (DAS) transformation, using the harmonic (H), geometric (G), or arithmetic (A) mean of study-specific sample sizes, or using the inverse of the variance (IV) of the synthesized result, as the overall sample size.
Figure 5.
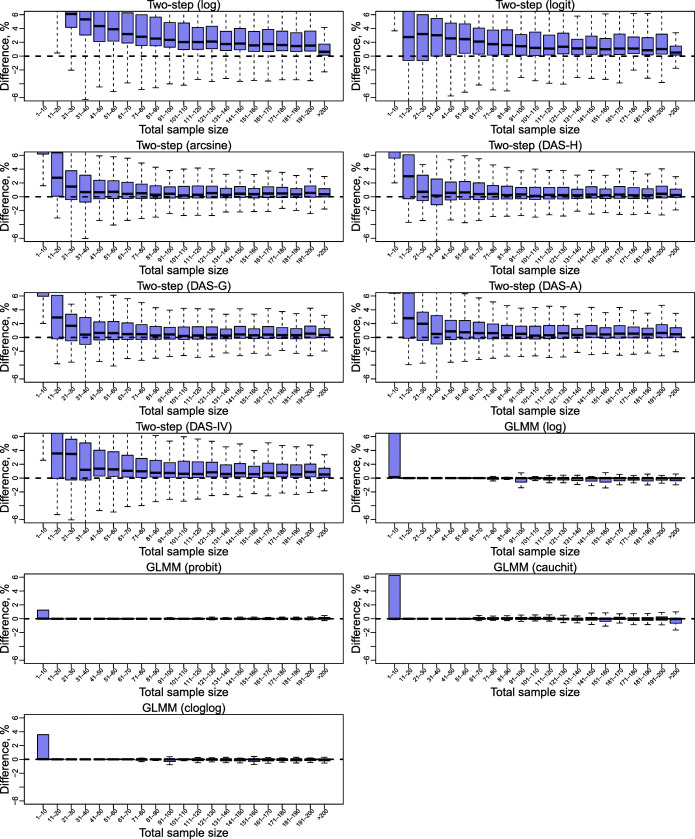
Box plots of absolute differences between overall proportion estimates (in percentage) produced by various meta-analysis methods and those by the generalized linear mixed model with the logit link among Cochrane datasets, categorized by the total sample size within a meta-analysis. In each panel, the horizontal dashed line represents no difference. Because many datasets led to extreme values of absolute differences, the box plots do not present outliers, and the vertical axis only presents the range from − 6 to 6%. The two-step method (DAS-H, DAS-G, DAS-A, or DAS-IV) corresponds to the Freeman–Tukey double-arcsine (DAS) transformation, using the harmonic (H), geometric (G), or arithmetic (A) mean of study-specific sample sizes, or using the inverse of the variance (IV) of the synthesized result, as the overall sample size.
In addition, Figure S21 gives the histogram of differences in AIC values. Many datasets had differences in AIC around 0, indicating no substantial differences between the GLMMs’ performance. However, there were still a noticeable number of datasets with large differences in AIC, especially for the GLMM with the cauchit link. For the GLMM with the log, probit, cauchit, and cloglog links, 2884 (7.4%), 9365 (23.5%), 6490 (17.5%), and 3703 (9.3%) datasets had differences in AIC < − 5, respectively, indicating substantially better performance than the reference method of the GLMM with the logit link; 16,825 (43.2%), 9558 (24.0%), 17,468 (47.2%), and 13,002 (32.5%) datasets had differences in AIC > 5, indicating substantially worse performance than the reference method.
DISCUSSION
This article has investigated 12 two-step and one-step methods for meta-analyses of proportions. This is the largest study in the current literature that compared the various methods using real-world (instead of simulated) data. Although the one-step GLMMs have been shown to outperform two-step methods with smaller biases and mean squared errors and higher CI coverage probabilities in simulation studies, they may lead to computation issues more frequently than the two-step methods, especially when sample sizes were small or proportions were close to 0% or 100%.
In general, the various methods produced similar overall proportion estimates with very high correlation coefficients and agreements. Although the popular Freeman–Tukey double-arcsine transformation has been recently criticized for its misleading conclusions in extreme scenarios (e.g., very diverse sample sizes across studies and small event counts),11 our results indicated that such scenarios were uncommon in practice. Moreover, it is a conventional practice for meta-analysts to report forest plots for displaying the collected studies’ distribution and funnel plots for assessing small-study effects. These plots require study-specific proportion estimates, which need to be obtained from the two-step methods. Our findings indicate that, in most cases, meta-analysts may safely use two-step methods for facilitating data visualizations.
Nevertheless, large absolute differences (e.g., > 6%) and large fold changes (e.g., > 2) existed for the two-step methods in certain cases. Large absolute differences were more likely to occur when the total sample sizes were small (e.g., < 50) or the crude event rates were about 10–20% and 90–95%. Large fold changes were more likely to occur when the total event counts were small (e.g., < 10) or the crude event rates were low (e.g., < 20%). Based on specific research purposes, meta-analysts should cautiously use the two-step methods in such cases.
In addition, the two-step methods generally produced narrower CIs than the GLMM with the logit link. These are in line with conclusions from existing simulation studies that the CIs produced by the two-step methods may have poor coverage probabilities. The CIs produced by the one-step GLMMs may be more suitable because the GLMMs fully account for within-study uncertainties.
This study has several limitations. First, meta-analyses of proportions are frequently used to synthesize prevalence from observational studies with very large sample sizes, while many studies from Cochrane reviews are randomized studies with smaller sample sizes. In this sense, event counts and crude event rates may be more important factors than sample sizes that may affect differences between methods for meta-analyses of prevalence. Second, because meta-analyses from the same Cochrane review investigated different but relevant interventions, outcomes, or subgroups on a specific topic, they may be associated to some extent, potentially affecting our conclusions. On average, each Cochrane review contributed approximately 13 meta-analyses. This problem could be avoided by extracting a single meta-analysis from each review, but it would lead to much fewer datasets and thus larger uncertainties in the results. Also, the criteria for choosing a single meta-analysis from each review might confound the results. Third, besides the 12 methods investigated in this article, other methods are available for synthesizing proportions, such as the beta-binomial model and Bayesian hierarchical models.15,28 These alternatives are seldom used in the current applications of meta-analyses of proportions, so this article did not investigate their empirical performance. In addition, we implemented GLMMs using the Laplace approximation for maximizing likelihoods. Alternative approaches such as the adaptive Gauss–Hermite approximation may also be used, and they may produce different results for GLMMs.29 Fourth, this article has limited to univariate proportions, while multivariate models (e.g., for simultaneously synthesizing sensitivities and specificities of diagnostic tests) may be more efficient by accounting for the correlations when multiple proportions are reported in each study.30
In summary, although different methods produced similar overall proportion estimates in most datasets, sensitivity analyses using both one- and two-step methods are recommended in the presence of small total event counts or sample sizes and very low or high event rates.
Supplementary Information
(PDF 968 kb)
Funding
This research was supported in part by the US National Institutes of Health/National Library of Medicine grant R01 LM012982 and National Institutes of Health/National Center for Advancing Translational Sciences grant UL1 TR001427. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. The financial support had no involvement in the conceptualization of the report and the decision to submit the report for publication.
Data Availability
The datasets and code for this study are available upon reasonable request from the corresponding author.
Declarations
This article focused on statistical methods for meta-analyses of proportions, and all analyses were performed based on published data. Therefore, this study did not require ethical approval and patient consent.
Conflict of Interest
The authors declare that they do not have a conflict of interest.
Footnotes
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Rothman KJ, Greenland S, Lash TL. Modern Epidemiology. Third ed. Philadelphia, PA: Lippincott Williams & Wilkins; 2008. [Google Scholar]
- 2.Rotenstein LS, Ramos MA, Torre M, Segal JB, Peluso MJ, Guille C, Sen S, Mata DA. Prevalence of depression, depressive symptoms, and suicidal ideation among medical students: a systematic review and meta-analysis. JAMA. 2016;316(21):2214–36. doi: 10.1001/jama.2016.17324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Borges Migliavaca C, Stein C, Colpani V, Barker TH, Munn Z, Falavigna M. How are systematic reviews of prevalence conducted? A methodological study. BMC Medical Research Methodology. 2020;20(1):96. doi: 10.1186/s12874-020-00975-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Jackson D, White IR. When should meta-analysis avoid making hidden normality assumptions? Biometrical Journal. 2018;60(6):1040–58. doi: 10.1002/bimj.201800071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Barendregt JJ, Doi SA, Lee YY, Norman RE, Vos T. Meta-analysis of prevalence. Journal of Epidemiology and Community Health. 2013;67(11):974–78. doi: 10.1136/jech-2013-203104. [DOI] [PubMed] [Google Scholar]
- 6.Freeman MF, Tukey JW. Transformations related to the angular and the square root. The Annals of Mathematical Statistics. 1950;21(4):607–11. doi: 10.1214/aoms/1177729756. [DOI] [Google Scholar]
- 7.Lin L, Xu C. Arcsine-based transformations for meta-analysis of proportions: pros, cons, and alternatives. Health Science Reports. 2020;3(3):e178. doi: 10.1002/hsr2.178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Allotey J, Stallings E, Bonet M, Yap M, Chatterjee S, Kew T, Debenham L, Llavall AC, Dixit A, Zhou D, Balaji R, Lee SI, Qiu X, Yuan M, Coomar D, van Wely M, van Leeuwen E, Kostova E, Kunst H, Khalil A, Tiberi S, Brizuela V, Broutet N, Kara E, Kim CR, Thorson A, Oladapo OT, Mofenson L, Zamora J, Thangaratinam S. Clinical manifestations, risk factors, and maternal and perinatal outcomes of coronavirus disease 2019 in pregnancy: living systematic review and meta-analysis. BMJ. 2020;370:m3320. doi: 10.1136/bmj.m3320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Warton DI, Hui FKC. The arcsine is asinine: the analysis of proportions in ecology. Ecology. 2011;92(1):3–10. doi: 10.1890/10-0340.1. [DOI] [PubMed] [Google Scholar]
- 10.Miller JJ. The inverse of the Freeman–Tukey double arcsine transformation. The American Statistician. 1978;32(4):138–38. [Google Scholar]
- 11.Schwarzer G, Chemaitelly H, Abu-Raddad LJ, Rücker G. Seriously misleading results using inverse of Freeman-Tukey double arcsine transformation in meta-analysis of single proportions. Research Synthesis Methods. 2019;10(3):476–83. doi: 10.1002/jrsm.1348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Stijnen T, Hamza TH, Özdemir P. Random effects meta-analysis of event outcome in the framework of the generalized linear mixed model with applications in sparse data. Statistics in Medicine. 2010;29(29):3046–67. doi: 10.1002/sim.4040. [DOI] [PubMed] [Google Scholar]
- 13.Platt RW, Leroux BG, Breslow N. Generalized linear mixed models for meta-analysis. Statistics in Medicine. 1999;18(6):643–54. doi: 10.1002/(SICI)1097-0258(19990330)18:6<643::AID-SIM76>3.0.CO;2-M. [DOI] [PubMed] [Google Scholar]
- 14.Chu H, Guo H, Zhou Y. Bivariate random effects meta-analysis of diagnostic studies using generalized linear mixed models. Medical Decision Making. 2010;30(4):499–508. doi: 10.1177/0272989X09353452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Siegel L, Rudser K, Sutcliffe S, Markland A, Brubaker L, Gahagan S, Stapleton AE, Chu H. A Bayesian multivariate meta-analysis of prevalence data. Statistics in Medicine. 2020;39(23):3105–19. doi: 10.1002/sim.8593. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Trikalinos TA, Trow P, Schmid CH. Simulation-based comparison of methods for meta-analysis of proportions and rates. AHRQ Publication No. 13(14)-EHC084-EF. U.S. Agency for Healthcare Research and Quality: Rockville, MD; 2013. [PubMed] [Google Scholar]
- 17.Lin L, Chu H. Meta-analysis of proportions using generalized linear mixed models. Epidemiology. 2020;31(5):713–17. doi: 10.1097/EDE.0000000000001232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Hamza TH, van Houwelingen HC, Stijnen T. The binomial distribution of meta-analysis was preferred to model within-study variability. Journal of Clinical Epidemiology. 2008;61(1):41–51. doi: 10.1016/j.jclinepi.2007.03.016. [DOI] [PubMed] [Google Scholar]
- 19.Riley RD, Lambert PC, Abo-Zaid G. Meta-analysis of individual participant data: rationale, conduct, and reporting. BMJ. 2010;340:c221. doi: 10.1136/bmj.c221. [DOI] [PubMed] [Google Scholar]
- 20.Kontopantelis E. A comparison of one-stage vs two-stage individual patient data meta-analysis methods: a simulation study. Research Synthesis Methods. 2018;9(3):417–30. doi: 10.1002/jrsm.1303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Bender R, Friede T, Koch A, Kuss O, Schlattmann P, Schwarzer G, Skipka G. Methods for evidence synthesis in the case of very few studies. Research Synthesis Methods. 2018;9(3):382–92. doi: 10.1002/jrsm.1297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Agresti A. Foundations of Linear and Generalized Linear Models. Hoboken, NJ: John Wiley & Sons; 2015. [Google Scholar]
- 23.Langan D, Higgins JPT, Jackson D, Bowden J, Veroniki AA, Kontopantelis E, Viechtbauer W, Simmonds M. A comparison of heterogeneity variance estimators in simulated random-effects meta-analyses. Research Synthesis Methods. 2019;10(1):83–98. doi: 10.1002/jrsm.1316. [DOI] [PubMed] [Google Scholar]
- 24.Noh M, Lee Y. REML estimation for binary data in GLMMs. Journal of Multivariate Analysis. 2007;98(5):896–915. doi: 10.1016/j.jmva.2006.11.009. [DOI] [Google Scholar]
- 25.Mills EJ, Kanters S, Thorlund K, Chaimani A, Veroniki A-A, Ioannidis JPA. The effects of excluding treatments from network meta-analyses: survey. BMJ. 2013;347:f5195. doi: 10.1136/bmj.f5195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Pereira TV, Horwitz RI, Ioannidis JPA. Empirical evaluation of very large treatment effects of medical interventions. JAMA. 2012;308(16):1676–84. doi: 10.1001/jama.2012.13444. [DOI] [PubMed] [Google Scholar]
- 27.Burnham KP, Anderson DR. Multimodel inference: understanding AIC and BIC in model selection. Sociological Methods & Research. 2004;33(2):261–304. doi: 10.1177/0049124104268644. [DOI] [Google Scholar]
- 28.Wong WL, Su X, Li X, Cheung CMG, Klein R, Cheng C-Y, Wong TY. Global prevalence of age-related macular degeneration and disease burden projection for 2020 and 2040: a systematic review and meta-analysis. The Lancet Global Health. 2014;2(2):e106–e16. doi: 10.1016/S2214-109X(13)70145-1. [DOI] [PubMed] [Google Scholar]
- 29.Ju K, Lin L, Chu H, Cheng L-L, Xu C. Laplace approximation, penalized quasi-likelihood, and adaptive Gauss–Hermite quadrature for generalized linear mixed models: towards meta-analysis of binary outcome with sparse data. BMC Medical Research Methodology. 2020;20(1):152. doi: 10.1186/s12874-020-01035-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Chu H, Cole SR. Bivariate meta-analysis of sensitivity and specificity with sparse data: a generalized linear mixed model approach. Journal of Clinical Epidemiology. 2006;59(12):1331–32. doi: 10.1016/j.jclinepi.2006.06.011. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(PDF 968 kb)
Data Availability Statement
The datasets and code for this study are available upon reasonable request from the corresponding author.