Figure 2: The geometry of abstraction.

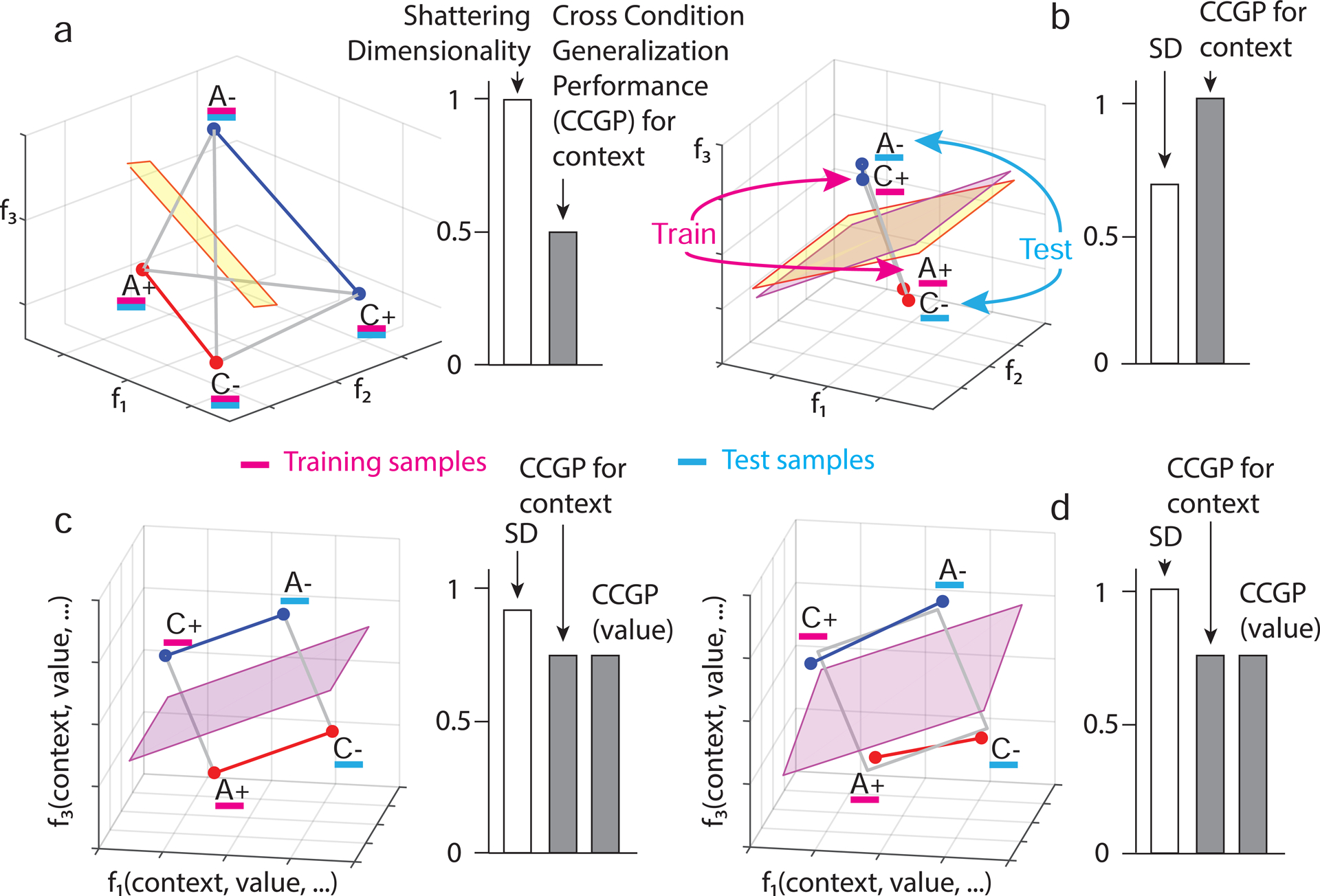
Different representations of context can have distinct geometries, each with different generalization properties. Each panel depicts in the firing rate space points that represent the average firing rate of 3 neurons in only 4 of the 8 conditions from experiments. The 4 conditions are labeled according to stimulus identity (A,C) and reward value (+,−). a. A random representation (points are at random locations in the firing rate space), which allows for decoding of context. The yellow plane represents a linear decoder that separates the 2 points of context 1 (red) from the 2 points of context 2 (blue). The decoder is trained on a subset of trials from all conditions (purple) and tested on held out trials from the same conditions (cyan) (see Figure S1a for more details). All other variables corresponding to different dichotomies of the 4 points can also be decoded using a linear classifier; hence the shattering dimensionality (SD) is maximal, but CCGP is at chance (right histogram). b. Abstraction by clustering: points are clustered according to context. A linear classifier is trained to discriminate context on rewarded conditions (purple). Its generalization performance (CCGP) is tested on unrewarded conditions not used for training (cyan). The separating plane when trained on rewarded conditions (purple) is different from the one obtained when all conditions are used for training (yellow), but for this clustered geometry, both planes are very similar. With clustered geometry, CCGP is maximal for context, but context is also the only variable encoded. Hence, SD is close to chance (right histogram). (See Methods S2 Clustering index as a measure of abstraction). Notice that the form of generalization CCGP involves is different from traditional decoding generalization to held out trials (see Methods S3 Relation between CCGP and decoding performance in classification tasks). c. Multiple abstract variables: factorized/disentangled representations. The 4 points are arranged on a square. Context is encoded along the direction parallel to the two colored segments, and value is in the orthogonal direction. In this arrangement, CCGP for both context and value are high; the SD is high but not maximal because the combinations of points that correspond to an exclusive OR (XOR) are not separable. Individual neurons exhibit linear mixed selectivity (see Methods S6 Selectivity and abstraction in a general linear model of neuronal responses). d. Distorted square: a sufficiently large perturbation of the points makes the representation higher dimensional (points no longer lie on a plane); a linear decoder can now separate all possible dichotomies, leading to maximal SD, but at the same time CCGP remains high for both value and context. See Methods S5 The trade off between dimensionality and our measures of abstraction and Fig. S2 that constructs geometries that have high SD and CCGP at the same time.