Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2021 Jul 6;15(7):11898–11907. doi: 10.1021/acsnano.1c03012

Out-of-Plane Transport of 1T-TaS2/Graphene-Based van der Waals Heterostructures

Carla Boix-Constant †, Samuel Mañas-Valero †,*, Rosa Córdoba †, José J Baldoví †, Ángel Rubio ‡,§, Eugenio Coronado †,*
PMCID: PMC8454993  PMID: 34228445

Abstract

graphic file with name nn1c03012_0006.jpg

Due to their anisotropy, layered materials are excellent candidates for studying the interplay between the in-plane and out-of-plane entanglement in strongly correlated systems. A relevant example is provided by 1T-TaS2, which exhibits a multifaceted electronic and magnetic scenario due to the existence of several charge density wave (CDW) configurations. It includes quantum hidden phases, superconductivity and exotic quantum spin liquid (QSL) states, which are highly dependent on the out-of-plane stacking of the CDW. In this system, the interlayer stacking of the CDW is crucial for interpreting the underlying electronic and magnetic phase diagram. Here, atomically thin-layers of 1T-TaS2 are integrated in vertical van der Waals heterostructures based on few-layers graphene contacts and their electrical transport properties are measured. Different activation energies in the conductance and a gap at the Fermi level are clearly observed. Our experimental findings are supported by fully self-consistent DFT+U calculations, which evidence the presence of an energy gap in the few-layer limit, not necessarily coming from the formation of out-of-plane spin-paired bilayers at low temperatures, as previously proposed for the bulk. These results highlight dimensionality as a key effect for understanding quantum materials as 1T-TaS2, enabling the possible experimental realization of low-dimensional QSLs.

Keywords: 2D materials, van der Waals heterostructures, quantum materials, electrical properties, DFT calculations

Low-dimensional materials offer appealing examples for studying strongly correlated materials with tantalizing physical phenomena such as superconductivity or magnetism.1−3 A relevant example in this context is provided by transition metal dichalcogenides (TMDCs). These compounds, with general formula MX2 (where M is a transition metal and X is a chalcogen), are formed by the stacking of X-M-X layers united through van der Waals interactions (see Figure 1.a).4−7 The physical properties of these layered materials range from insulators to superconductors and, as recently discovered, some of them show intrinsic magnetic properties.8,9

Figure 1.

Figure 1

Open in a new tab

Crystal structure and charge density wave (CDW) arrangement in 1T-TaS2. (a) Unit cell in dash lines. (b) In-plane structure where it has been highlighted the formation of the Stars-of-David, corresponding to the commensurate charge density wave phase (gray line) as well as the triangular lattice of spin 1/2 (turquoise line) that forms the quantum spin liquid. (c) Different out-of-plane stacking configurations of the CDW: AL stacking (left), L stacking (center) and A stacking (right), following the notation of reference (33). Sulfur atoms are represented in yellow and tantalum ones in brown. For clarity, the central tantalum of the Star-of-David (S = 1/2) has been marked in red and the different stacking configurations with green lines. The red, green and blue colors of the axis correspond to the a, b, and c axis, respectively. For simplicity, in c it has been only represented the tantalum atoms.

In particular, 1T-TaS2 is one of the most studied TMDCs due to its unexpected physical properties. Like the rest of group V TMDCs, this compound should be in theory a metal. However, it behaves as a semiconductor and does not show long-range magnetic order even at milliKelvin temperature.10,11 Indeed, motivated by these intriguing properties, Philip W. Anderson developed his resonance band model.12 A key ingredient of this material are the charge density waves (CDW) —periodical localizations of the charge— that are stable with different arrangements, yielding to metastable phases, quantum hidden states,13 and even quantum spin liquid (QSL) phases11,14,15 and superconductivity when doped or under pressure.16−21 Upon cooling, the thermal behavior of bulk 1T-TaS2 shows the formation of an incommensurate charge density wave (I-CDW) at 350 K, followed by a nearly commensurate CDW (N-CDW) to a commensurate CDW (C-CDW) transition around 200 K, generally ascribed as a Mott transition.22 The previous transitions are accompanied by a characteristic hysteresis behavior, as shown by transport measurements or magnetic susceptibility.23 The CDW arranges forming the so-called Star-of-David, where every 13 Ta atoms are coupled. In 12 of them, their spins are paired (marked in brown in Figure 1b,c), while the central one contains a S = 1/2 (marked in red in Figure 1b,c) which forms a triangular lattice below 200 K (Figure 1b).24 This triangular lattice is magnetically frustrated due to the existing antiferromagnetic correlations and is the basis for the possible emerging QSL, as proposed both theoretically14 and experimentally by different techniques.11,15,25

In the monolayer limit, the QSL ground state is theoretically demonstrated14 but, in the multilayer case, the out-of-plane pairing of the Star-of-David has to be considered (see Figure 1c). For instance, if out-of-plane correlations between the layers are absent (A or L stacking, Figure 1c), then the Mott scenario is valid and the QSL is formed; meanwhile, if the Stars-of-David form dimers in the out-of-plane direction as spin paired bilayers (AL stacking, Figure 1c), the system has just to be considered as a conventional band insulator, thus, not being a QSL.14,26 Nonetheless, these options do not need to exclude each other necessarily since they can occur at different temperature regimes.27 Thus, studying the out-of-plane correlations is a key element for understanding the underlying electronic and magnetic scenario occurring in 1T-TaS2.

Notice that, so far, most of the studies on 1T-TaS2 have been focused on bulk samples, both from the theoretical and experimental points of view and the out-of-plane metallic character of the bulk is still under debate. From the experimental side, different interlayer mechanisms have been proposed and the conventional Mott picture, dimerization and the formation of domain wall networks, among others, are being revisited.27−31 Theoretically, some authors have proposed metallic band dispersion along the out-of-plane direction if the Stars-of-David are coupled vertically (A stacking, Figure 1c), or through a diagonal (L stacking, Figure 1c) and an insulating gap in the case of the formation of bilayers (AL stacking, Figure 1c).32,33 However, more recent calculations applying a self-consistent DFT+U generalized basis approach that covers the whole Star-of-David point toward a Mott gap in the bulk, independently of the out-of-plane stacking configuration of the Stars-of-David.34

It is worthwhile to mention that the previous discussions are hold regarding bulk 1T-TaS2 but atomically thin layers do not necessarily behave in the same way as a consequence of their reduced dimensionality. In the thin-layer regime (thickness below 10 nm), several experiments have been performed in order to unveil the CDW phase diagram of 1T-TaS2.20,22 In fact, the fine-tuning of the CDW has been achieved by using conventional electrodes and applying current pulses,35 bias voltage,36 light,37,38 strain,39 or its deposition on different substrates,40 among others. With devices based on van der Waals heterostructures (vdWHs), the few examples reported so far have involved transport measurements on thin-layers of 1T-TaS2 contacted to graphene,41 MoS2,42 or black phosphorus43 in a typical in-plane configuration. Only bulky samples (thicknesses of hundreds of nanometers)28,29,44 or devices incorporating superconducting NbSe245 have been measured in a vertical configuration. Hence, the out-of-plane CDW structure of 1T-TaS2 in the thin-layer limit remains unexplored. In this work we present the fabrication and electrical characterization of vertical vdWHs based on 1T-TaS2 thin-layers interfaced with few-layers graphene.

Results and Discussion

The vdWHs fabrication is based on the successive deterministic transfer of the 2D materials and is implemented inside an argon glovebox.46 From the mechanical exfoliation of the flakes and its inspection to the vdWH assembly and electrical transport measurements, the vdWHs are not exposed to air (see Methods for further details). This is a key factor since thin-layers of 1T-TaS2 degrade in ambient conditions.20,35 The identification of thin-layers of 1T-TaS2 on 285 nm SiO2/Si substrates is performed by optical microscopy. The optimal contrast region is observed for the green channel of the visible spectrum, as it is experimentally and theoretically investigated within the Fresnel framework in the Supporting Information (SI) Section 1. The vdWH consists on a 1T-TaS2 thin-layer sandwiched via van der Waals forces between few-layers graphene that are placed on top of the metallic contacts (Figure 2a,b). Although the geometrical factors cannot be fully controlled within the present vdWH approach, it benefits of being fully integrated under inert atmosphere conditions, thus being an excellent option for studying air-unstable 2D materials, as recently performed with some highly unstable 2D magnets as CrI3.47 The electrical-transport characterization is performed by standard four-probe configuration: a current is injected through the whole vdWH by the outer leads and the voltage drop is measured using the inner ones (Figure 2a,b; see Methods for technical details). Figure 2d shows a scanning transmission electron microscopy (STEM) image of an area of the cross-sectional view of the vertical vdWH, where 5 layers of 1T-TaS2 can be clearly identified (see Methods and SI Section 5 for other vdWHs).

Figure 2.

Figure 2

Open in a new tab

Vertical van der Waals heterostructures (vdWHs) based on 1T-TaS2. (a) Optical image of the vdWH and electronic transport configuration. For clarity, the different flakes are enclosed with dashed lines: the bottom h-BN in red, the bottom contact in purple, the 1T-TaS2 flake in orange, the top contact in blue and the top h-BN in green. Scale bar: 20 μm. (b) Artistic representation —not to scale— of the vdWH with the back gate voltage configuration sketched. In dark yellow it is represented the metal contacts, in purple the bottom FLG contact, in green the top FLG contact and, in yellow, the 1T-TaS2 thin-layer. (c) Electrical transport properties of a nine layers 1T-TaS2 vdWH (device A in the SI) and Arrhenius plot (inset). The dashed lines highlight the different transitions described in the literature for bulk 1T-TaS2 (see main text). In particular, from I-CDW to N-CDW at 350 K (purple), from N-CDW to C-CDW at 200 K (red), from C-CDW to H-CDW at ca. 50 K (green) and the QSL crossovers described at 100 K (yellow) and 25 K (blue). (d) STEM image of a vdWH showing 5 layers of 1T-TaS2 (device D in the SI). Scale bar: 5 nm. (e) Comparative of in-plane (data from Yu et al.(20) and Yoshida et al.(22)) and out-of-plane (this work; the 1T-TaS2 thickness in nm is obtained by atomic force microscopy whereas the number of layers in brackets is determined by STEM images) transport measurements on 1T-TaS2 atomically thin layers. Reported transitions temperatures on bulk 1T-TaS2 are highlighted with dashed lines as in c. Comparative with bulk data and a close inspection around the 350 K region is presented in SI Figures S.7 and S.8.

A total of nine different vdWHs with 1T-TaS2 thickness ranging from three to nine layers are fabricated and their electrical transport properties inspected (the characterization of all the vdWHs is discussed in the SI). All the heterostructures exhibit an ohmic behavior with linear IV curves (see SI Section 4), in agreement with the absence of a Schottky barrier in our devices. The electrical properties of a representative device (device A in the SI) are shown in Figure 2c. As reference, the different transitions reported in the literature for bulk 1T-TaS2 are also plotted in the figures as vertical dashed lines: 350 K (I-CDW),48 200 K (C-CDW),48 100 K (QSL crossover),49 50 K (H-CDW and QSL crossover)13,15,28,50 and 25 K (QSL crossover).49 The characteristic hysteretic transition from I-CDW to N-CDW transition at 350 K (Figure 2c and SI Section 2) is clearly observed even in our thinnest vdWH (3 layers; SI Sections 2, 4, and 5), in contrast to previous reports where it was absent for thicknesses below 3.5 nm (ca. 6 layers).20 We attribute it to the fact of working under strict inert atmosphere conditions that avoid the oxidation of 1T-TaS2. While cooling down, the vdWH resistance increases without exhibiting the abrupt hysteresis around 200 K observed in bulk samples (Figure 2c and SI Figure S.7), as attributed to the reduced dimensionality of the 1T-TaS2 thin-layers.51 We note that the absence of this hysteresis in thin-layers does not imply that the commensurate CDW is not formed. For example, Sakabe et al.52 have observed a commensurate CDW phase in trilayer 1T-TaS2 by transmission electron microscopy at room temperature. In order to relate different devices, the resistance at different temperatures, R(T), is normalized, Rnorm, to the value of the resistance at the highest temperature measured (ca. 400 K), R(HT) (see Figure 2e and SI Section 3), thus Rnorm = R(T)/R(HT). In Figure 2e, SI Figures S.7 and S.8 and Section 2, measurements of different horizontal devices are compared to those of vertical ones (this work). In these vertical heterostructures, Rnorm is ca. two times lower in the high temperature regime and several orders of magnitude at low temperatures (2 K), reflecting that the insulating state due to the in-plane commensuration of the Star-of-David formation (hysteretic behavior at 350 K) is affecting more the overall transport properties of the horizontal devices. This is in line with transport measurements in bulk 1T-TaS2, which show a much smaller resistance change at 350 K in the out-of-plane direction compared to the in-plane one.29 From all these observations, it is inferred that the out-of-plane contribution is the dominant term in our vertical devices. All measured vdWHs exhibit similar trends (see SI).

The vdWH resistance in the present case has two main contributions: the intrinsic 1T-TaS2 resistance (formed by the in-plane and the out-of-plane resistances in parallel) and the contact resistance at the interface, Rinterface (formed between the few-layers graphene and 1T-TaS2).28Rinterface is not expected to exhibit a temperature dependence unless an electronic gap or barrier –as, for example, a Schottky barrier– is formed.53 A simple way to consider these transitions is by assuming that the transport properties for distinct CDW configurations are associated with different activation energies. This can be modeled by an Arrhenius law, where the conductance, G, is of the form G = G0·exp(−Ea/kBT), being G0 a prefactor, Ea the activation energy, kB the Boltzmann constant and T the temperature.54 Other mechanisms, as variable range or nearest-neighbor hopping conduction,55 are also considered (see SI Section 3), not observing any single transport mechanism suitable for all the temperature range. In the Arrhenius plots (Figure 2c and SI Section 3), two linear regimes are investigated: one at low temperatures (LT) and one in the N-CDW region (200 K to 350 K). The present data shows a progressive transition between the HT and LT regimes where different activation energies regimes can be found, without any sharp or abrupt transition below 350 K, in stark contrast with bulk 1T-TaS2.28 The involved activation energies are in the order of 0.05 and 11 meV, for the LT and HT regimes, respectively. The value for the HT phase is comparable with the one reported by Svetin et al.(28) for bulky samples (10 meV) in the 40 K – 140 K range. Note that, in contrast to the results reported for bulk 1T-TaS2 in the out-of-plane direction,28,29 we do not find a linear regime below 200 K, nor the CDW hysteresis at 200 K. This underlines the possible electronic changes due to dimensionality effects (bulk crystals of ∼100 μm vs. atomically thin layers below 10 nm) and differences in the geometrical factors of the devices. The projection of the LT and HT fittings intercepts around 70 K. This temperature is in accordance with that proposed for the H-CDW to C-CDW transition reported by previous phototransport experiments.13,28

The use of a back gate voltage, Vg, allows the experimental access to the density of states of the vdWH. Although the 1T-TaS2 carrier density is high, requiring in principle the use of electrochemical techniques,20 it has been shown recently that a solid gate is effective when thin-layers of 1T-TaS2 are integrated in a heterostructure with other 2D materials, like black phosphorus or 2H-MoS2.42,43,56 As shown in Figure 3 for the vdWH of 9 1T-TaS2 layers (device A in the SI), at 200 K the conductance as a function of the back gate voltage presents a minimum that broadens and shifts toward 0 V upon cooling down, until a plateau is reached around 50 K and a second peak emerges at T < 25 K. This second minimum at Vg ∼ −2 V is related to the charge neutrality point of the few-layers graphene contacts. The behavior of the overall vdWH cannot be ascribed to the simple addition of the charge neutrality point of the bottom and top few-layers graphene (Figure 3a), as corroborated by performing DC IV curves at different back gate voltages and temperatures and comparing their resistances (SI Section 4.1). For clarity, in Figure 3b the conductance is normalized, ΔG, with respect to the value at zero voltage gate, being ΔG = {[G(Vg) – G(Vg = 0)]/ G(Vg = 0)}·100; thus, ΔG < 0 (red color in Figure 3b) represents a higher resistance that can be attributed to a lower density of states with respect to the case of Vg = 0. Assuming that the Fermi level of the whole vdWH resides at Vg = 0, it can be seen that at low temperatures an electronic gap emerges around Vg = 0. Since the charge neutrality point remains at the same position in the vdWH and in the few-layer graphene contacts, the origin of the plateau in conductance cannot be ascribed to different doping levels in the few-layer graphene flakes. This gap state shows a magnetic field dependence as well (Figure 4). At 2 K, the gap at Vg = 0 survives until a field of ca. 1 T and, while increasing the temperature, this value decreases (more detailed data can be seen in the SI Section 4.1, including the gate and field dependence in the −8 T to 8 T range for the vdWH and the top and bottom few-layers graphene). At high magnetic fields, the characteristic Landau levels of graphene that develop forming a Landau fan are observed.57 The overall same tendencies have been observed in several vdWHs (SI Sections 4.1, 4.2, 4.3, and 4.9), although the insulating gap size differs from sample to sample. This may be attributed to the different geometrical factors that yields to a different effective electric field between vdWHs.

Figure 3.

Figure 3

Open in a new tab

Conductance as a function of the back gate voltage of a 9 layers 1T-TaS2 heterostructure (device A in the SI). (a) Temperature dependence for the bottom few-layers graphene (FLG), the heterostructure and the top FLG. (b) Detailed view around Vg = 0 for the heterostructure where, for clarity, it has been added a contour plot, the values of ΔG = {[G(Vg) – G(Vg = 0)]/G(Vg) = 0)}·100 and dashed lines for the previous reported transitions in bulk 1T-TaS2 (C-CDW to H-CDW transition at ca. 50 K —green— and the QSL crossovers at 100 K —yellow—and 25 K —blue—).

Figure 4.

Figure 4

Open in a new tab

Conductance as a function of the back gate voltage and perpendicular external magnetic field for the 9 layers 1T-TaS2 heterostructure (device A in the SI) at 2 K, 40 and 140 K.

In order to explore the nature of the insulating behavior observed in the conductance experiments, we carry out first-principles calculations for different number of 1T-TaS2 layers. Owing to the strong correlation of electrons in the d orbitals of the Ta atoms due to the CDW formation, we adopt a spin-polarized DFT+U approach, where U is the on-site Coulomb repulsion. We estimate self-consistently a Hubbard U of 2.86 eV for the d orbitals of the central Ta in the Star-of-David using density functional perturbation theory (DFPT)58 in QuantumEspresso.59 This value is in accordance with the obtained U from other authors (2.94 eV) using the same DFPT method for the undeformed structure.29 The 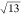Inline graphic × Inline graphic supercells for 1 layer, 2 layers, 3 layers, 4 layers, and bulk (containing 2 layers) are fully optimized without constrains considering the Hubbard U in all cases. Then, we compute the electronic band structure for the different slabs and the bulk, applying U to the d orbitals of the Ta atoms of the whole Star-of-David (Figure 5). Indeed, our self-consistent ground state DFT+U calculations also support the formation of the commensurate CDW phase at low temperatures. In the monolayer, we have evaluated the Hubbard U based on an iterative recalculation until achieving consistency of the final Hubbard U parameter with the crystal structure following the protocol defined by Timrov et al.60 based on density-functional perturbation theory. This has resulted in the formation of the Stars-of-David with average distances of 12.13 Å between the central Ta atoms of neighboring Stars-of-David.

Figure 5.

Figure 5

Open in a new tab

Calculated band structure for C-CDW √13 × √13 supercells of 1T-TaS2 for (a) atomically thin layers (from one to four layers from left to right) and (b) bulk (blue/red refers to spin up/down). The Brillouin zone is depicted in c. (d) Thickness dependence of the gap.

In Figure 5.a one observes that the in-plane bands (Γ-M-K- Γ) are gapped around the Fermi energy, independently of the number of layers. This is due to the formation of a commensurate CDW in the material, which avoid the in-plane hopping between neighboring Stars-of-David. On the contrary, the out-of-plane bands (Γ-A) exhibit marked band dispersion in the bulk in agreement with previous calculations in the literature (Figure 5.b),32−34 displaying a Mott gap (∼0.19 eV) that is dependent on U and can be suppressed by the application of external stimuli such as moderate hydrostatic pressure.29 This band dispersion flattens when the dimensionality is reduced and a more robust bandgap appears, which is independent of the Stars-of-David stacking and the degree of correlation (see SI Section 6), being enhanced when the number of layers is reduced (from 0.19 eV in the 4 layers slab to 0.39 eV in the monolayer, Figure 5.a). Therefore, this gap, which is intrinsic to the monolayer, can also be taken as a fingerprint of the few-layers 1T-TaS2 system. It arises from the confinement of the electrons within the Star-of-David, either in-plane as well as out-of-plane, as illustrated by the flat character of the band dispersion near the Fermi level in the few-layer limit. This is in sharp contrast with the bulk where a dispersive band near the Fermi level is predicted, thus facilitating the out-of-plane delocalization. This manifests that dimensionality effects play a key role in the electronic behavior of 1T-TaS2 in such a way that the observed insulating behavior is not necessarily due to the formation of out-of-plane spin-paired bilayers at low temperatures, as theoretically proposed for the bulk case.32,33 In order to evaluate the effect of the few-layer graphene on the band structure of 1T-TaS2, we optimized a heterostructure formed by a 1T-TaS2 monolayer sandwiched between two layers of graphene. We combined a 5 × 5 supercell of graphene with the fully relaxed 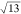Inline graphic × Inline graphic unit cell of the commensurate CDW 1T-TaS2 monolayer. The electronic structure (see SI Section 6) shows the lack of hybridization between the electronic states of both materials. The bandgap of the 1T-TaS2 has been slightly reduced to 0.29 eV and the graphene Dirac cone appears embedded in the conduction band of the 1T-TaS2 at about 0.33 eV, without inducing any dispersion in the out-of-plane direction (Γ-A direction). Thus, we can infer that the few-layers graphene used in the experiment is not affecting significantly the 2D CDW sheet, which preserves its structural and electronic properties.

Conclusion

Different CDW multistable configurations are explored in air-unstable thin-layers of 1T-TaS2 by the fabrication of vertical van der Waals heterostructures with few-layers graphene. Based on an Arrhenius model, a progressive transition with different activation energies is observed from 200 K (C-CDW) to the lowest temperature with a slope change at ca. 70 K. In addition, a gap in the Fermi level emerges at low temperatures. The present results, supported by fully self-consistent DFT+U calculations, highlight the electron confinement across the layers when approaching to the two-dimensional limit. In fact, as a result of the reduced dimensionality, a band flattening in the out-of-plane direction is predicted, in clear contrast to the bulk.

So far, the requisites for stabilizing a QSL state in these layered materials are (i) to have a frustrated spin network with antiferromagnetic correlations (encountered here by a commensurate Star-of-David structure), (ii) to have electron confinement (in-plane as well as out-of-plane localization), and (iii) to have an odd number of electrons per unit cell (even numbers, for example bilayers, yield to a conventional band insulator). In the present case, the first requirement is fulfilled and we have demonstrated the second one, both experimentally and theoretically. As far as the third condition is concerned, this remains elusive with the techniques used in this work (transport measurements). However, it is worth noting that we have observed the formation of a gap in atomically thin layers of 1T-TaS2 having an odd number of layers (3, 5, and 9 layers, as proved by cross-section STEM; see SI Section 5). Hence, even in the presence of a bilayer paring, in these specific cases an unpaired layer would remain, where a QSL could exist. This would be highly relevant to the fields of quantum information and communication as it could enable the use of low dimensional 1T-TaS2 materials for fabricating devices based on 2D van der Waals heterostructures displaying large entanglement effects.

Methods

Crystal Growth of 1T-TaS2

High quality crystals were grown by chemical vapor transport (CVT) using iodine as a transport agent, as already reported by some of us.49

Exfoliation, Characterization, and Manipulation of Atomically Thin Layers

1T-TaS2 crystals and natural graphite were mechanically exfoliated using adhesive tape (80 μm thick adhesive plastic film from Ultron Systems) inside an argon glovebox. The exfoliated samples were inspected primarily by optical microscopy (Nikon Eclipse LV-100 optical microscope with a Nikon TU Plan Fluor 100× objective lens of 1 mm working distance and a numerical aperture of 0.9 and 10 nm fwhm visible band-pass filters from Thorlabs) as a fast tool for the identification of thin-layers and atomic force microscopy (Nano-Observer AFM from CSI Instruments) inside an argon glovebox. Following the recently developed fabrication of vertical vdWHs for studying air unstable 2D magnets, like CrI3 or MnPS3,47,61 the vertical vdWHs were built in a deterministic way using polycarbonate, as reported in reference46 and placed on top of prelithographed metal contacts fabricated by conventional electron beam lithography techniques (5 nm Ti/50 nm Pd) on 285 nm SiO2/Si substrates (from NOVA Electronic Materials, LLC).

Electrical Measurement Setup

Electrical measurements were performed in a Quantum Design PPMS-9 with a base temperature of 2 K, using conventional DC and AC lock-in techniques with a MFLI Lock-in Amplifier from Zurich Instruments at low frequencies (27.7 Hz). All shown measurements are performed in DC unless it is explicitly said that AC was applied. In order to perform current-bias experiments, an external resistance of 100 MΩ is used, that is, much larger than the resistance of the sample. Bottom back gate voltage was applied with a Keithley 2450. All temperature sweeps were performed at 1 K/min and field sweeps at 200 Oe/s.

TEM

Standard TEM cross-sectional sample preparation by using a FEI Helios Nanolab 650 Dual Beam instrument was carried out on the vertical vdWHs. Scanning transmission electron microscopy (STEM) imaging was carried out with a probe-corrected FEI Titan 60–300 operated at 300 kV and equipped with a high brightness X-FEG and a Cs CETCOR corrector for the condenser system to provide subangstrom probe size. STEM images are shown in SI Section 5.

Band Structure Calculations

DFT+U electronic structure calculations were performed using the Quantum ESPRESSO package.59 Exchange-correlation energy is described considering the Perdew–Burke–Ernzerhof (PBE) generalized gradient approximation (GGA) functional. We use standard solid-state pseudopotentials (SSSP) from the efficiency library of Materials Cloud.62,63 The electronic wave functions are expanded with well-converged kinetic energy cut-offs for the wave functions and charge density of 45 and 360 Ry, respectively. The Brillouin zone was sampled by a fine Γ-centered 8 × 8 × 8 k-point Monkhorst–Pack mesh for the case of the bulk system and 8 × 8 × 1 for the case of slab calculations. Dispersion corrections to account for van der Waals interactions between the 1T-TaS2 layers are considered by applying semiempirical Grimme-D3 corrections. All the structures are fully optimized using the Broyden-Fletcher-Goldfarb-Shanno (BFGS) algorithm until the forces on each atom are smaller than 1 × 10–3 Ry/au and the energy difference between two consecutive relaxation steps is less than 1 × 10–4 Ry. The Hubbard U is determined self-consistently using used the simplified version proposed by Dudarev et al.64 using density functional perturbation theory.58

Acknowledgments

We thank Á. López-Muñoz for his constant technical support and helpful discussions. The electron microscopy measurements have been conducted in the “Laboratorio de Microscopías Avanzadas” at “Instituto de Nanociencia de Aragón - Universidad de Zaragoza” (LMA-INA). We acknowledge I. Rivas for TEM sample preparation and A. Ibarra for the assistance in the TEM measurements.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsnano.1c03012.

  • Optical contrast of 1T-TaS2 on SiO2/Si substrates, comparative of in-plane vs. out-of-plane devices, geometrical factors, Arrhenius and hopping analysis of the transport data, supplementary transport measurements for all the different measured van der Waals heterostructures and band structure calculations. This manuscript has been previously submitted to arXiv preprint server: Boix-Constant, C.; Mañas-Valero, S.; Córdoba, R.; Baldoví, J.J.; Rubio, Á.; Coronado, E. Out-of-Plane Transport of 1T-TaS2/Graphene-Based van der Waals Heterostructures. 2021, 2009.14550v2. arXiv.https://arxiv.org/abs/2009.14550v2 (accessed 2021/4/2) (PDF)

Author Contributions

C.B.-C. and S.M.-V. grown and characterized the 1T-TaS2 crystals, performed the exfoliation, optical contrast, heterostructure fabrication, transport measurements and data analysis. R.C. performed the e-beam lithography and helped with TEM measurements and device fabrication. J.J.B. performed the DFT+U calculations. J.J.B. interpreted the electronic structure calculations with the supervision of A.R. S.M.-V. conceived the work and coordinated the experiments. E.C. and S.M.-V. supervised the project and the preparation of the manuscript. All authors discussed the results and commented on the manuscript. All authors have given approval to the final version of the manuscript.

We acknowledge the financial support from the European Union (ERC AdG Mol-2D 788222 and ERC-2015-AdG-694097), the Spanish MICINN (MAT2017-89993-R cofinanced by FEDER and Excellence Unit “María de Maeztu”, CEX2019-000919-M), the Generalitat Valenciana (Prometeo program and PO FEDER Program, ref IDIFEDER/2018/061 and IDIFEDER/2020/063), the Basque government (Grupos Consolidados, IT1249-19) and the Deutsche Forschungsgemeinschaft (DFG) under Germany’s Excellence Strategy - Cluster of Excellence Advanced Imaging of Matter (AIM) EXC 2056-390715994 and funding by the Deutsche Forschungsgemeinschaft (DFG) under RTG 1995 and GRK 2247. Support by the Max Planck Institute - New York City Center for Non-Equilibrium Quantum Phenomena is acknowledged. R.C. acknowledges the support of a fellowship from “la Caixa” Foundation (ID 100010434). The fellowship code is LCF/BQ/PR19/11700008. J.J.B. thanks support from the Plan Gent of Excellence of the Generalitat Valenciana (CDEIGENT/2019/022). C.B.-C. thanks the Generalitat Valencia for a PhD fellowship.

The authors declare no competing financial interest.

Supplementary Material

nn1c03012_si_001.pdf (33.6MB, pdf)

References

  1. Bader S. D. Magnetism in Low Dimensionality. Surf. Sci. 2002, 500 (1–3), 172–188. 10.1016/S0039-6028(01)01625-9. [DOI] [Google Scholar]
  2. Huang B.; Clark G.; Navarro-Moratalla E.; Klein D. R.; Cheng R.; Seyler K. L.; Zhong D.; Schmidgall E.; McGuire M. A.; Cobden D. H.; Yao W.; Xiao D.; Jarillo-Herrero P.; Xu X. Layer-Dependent Ferromagnetism in a van der Waals Crystal down to the Monolayer Limit. Nature 2017, 546 (7657), 270–273. 10.1038/nature22391. [DOI] [PubMed] [Google Scholar]
  3. Navarro-Moratalla E.; Island J. O.; Mañas-Valero S.; Pinilla-Cienfuegos E.; Castellanos-Gomez A.; Quereda J.; Rubio-Bollinger G.; Chirolli L.; Silva-Guillén J. A.; Agraït N.; Steele G. A.; Guinea F.; van der Zant H. S. J.; Coronado E. Enhanced Superconductivity in Atomically Thin TaS2. Nat. Commun. 2016, 7, 11043. 10.1038/ncomms11043. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Roldán R.; Chirolli L.; Prada E.; Silva-Guillén J. A.; San-Jose P.; Guinea F. Theory of 2D Crystals: Graphene and Beyond. Chem. Soc. Rev. 2017, 46 (15), 4387–4399. 10.1039/C7CS00210F. [DOI] [PubMed] [Google Scholar]
  5. Manzeli S.; Ovchinnikov D.; Pasquier D.; Yazyev O. V.; Kis A. 2D Transition Metal Dichalcogenides. Nat. Rev. Mater. 2017, 2, 17033. 10.1038/natrevmats.2017.33. [DOI] [Google Scholar]
  6. Wang H.; Feng H.; Li J. Graphene and Graphene-Like Layered Transition Metal Dichalcogenides in Energy Conversion and Storage. Small 2014, 10 (11), 2165–2181. 10.1002/smll.201303711. [DOI] [PubMed] [Google Scholar]
  7. Koski K. J.; Cui Y. The New Skinny in Two-Dimensional Nanomaterials. ACS Nano 2013, 7 (5), 3739–3743. 10.1021/nn4022422. [DOI] [PubMed] [Google Scholar]
  8. Mañas-Valero S.; García-López V.; Cantarero A.; Galbiati M. Raman Spectra of ZrS2 and ZrSe2 from Bulk to Atomically Thin Layers. Appl. Sci. 2016, 6 (9), 264. 10.3390/app6090264. [DOI] [Google Scholar]
  9. Tsen a. W.; Hunt B.; Kim Y. D.; Yuan Z. J.; Jia S.; Cava R. J.; Hone J.; Kim P.; Dean C. R.; Pasupathy a. N. Nature of the Quantum Metal in a Two-Dimensional Crystalline Superconductor. Nat. Phys. 2016, 12 (3), 208–212. 10.1038/nphys3579. [DOI] [Google Scholar]
  10. Wilson J. A.; Yoffe A. D. The Transition Metal Dichalcogenides Discussion and Interpretation of the Observed Optical, Electrical and Structural Properties. Adv. Phys. 1969, 18 (73), 193–335. 10.1080/00018736900101307. [DOI] [Google Scholar]
  11. Kratochvilova M.; Hillier A. D.; Wildes A. R.; Wang L.; Cheong S.-W.; Park J.-G. The Low-Temperature Highly Correlated Quantum Phase in the Charge-Density-Wave 1T-TaS2 Compound. npj Quantum Mater. 2017, 2 (1), 42. 10.1038/s41535-017-0048-1. [DOI] [Google Scholar]
  12. Anderson P. Who or What Is RVB?. Phys. Today 2008, 61 (4), 8–9. 10.1063/1.2911190. [DOI] [Google Scholar]
  13. Stojchevska L.; Vaskivskyi I.; Mertelj T.; Kusar P.; Svetin D.; Brazovskii S.; Mihailovic D. Ultrafast Switching to a Stable Hidden Quantum State in an Electronic Crystal. Science 2014, 344 (6180), 177–180. 10.1126/science.1241591. [DOI] [PubMed] [Google Scholar]
  14. Law K. T.; Lee P. A. 1T-TaS2 as a Quantum Spin Liquid. Proc. Natl. Acad. Sci. U. S. A. 2017, 114 (27), 6996–7000. 10.1073/pnas.1706769114. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Klanjšek M.; Zorko A.; Žitko R.; Mravlje J.; Jagličić Z.; Biswas P. K.; Prelovšek P.; Mihailovic D.; Arčon D. A High-Temperature Quantum Spin Liquid with Polaron Spins. Nat. Phys. 2017, 13 (11), 1130–1134. 10.1038/nphys4212. [DOI] [Google Scholar]
  16. Ritschel T.; Trinckauf J.; Koepernik K.; Büchner B.; Zimmermann M. V.; Berger H.; Joe Y. I.; Abbamonte P.; Geck J. Orbital Textures and Charge Density Waves in Transition Metal Dichalcogenides. Nat. Phys. 2015, 11 (4), 328–331. 10.1038/nphys3267. [DOI] [Google Scholar]
  17. He R.; Ye Z.; Ye G.; Anderson H.; Dai X.; Wu X.; Hu J.; Liu Y.; Lu W.; Sun Y.; Pasupathy A. N.; Tsen A. W. Distinct Surface and Bulk Charge Density Waves in Ultrathin 1T-TaS2. Phys. Rev. B: Condens. Matter Mater. Phys. 2016, 94 (20), 1–6. 10.1103/PhysRevB.94.201108. [DOI] [Google Scholar]
  18. Suzuki A.; Koizumi M.; Doyama M. Thermal Evidences for Successive CDW Phase Transitions in 1T-TaS2. Solid State Commun. 1985, 53 (2), 201–203. 10.1016/0038-1098(85)90126-7. [DOI] [Google Scholar]
  19. Scruby C. B.; Williams P. M.; Parry G. S. The Role of Charge Density Waves in Structural Transformations of 1T TaS2. Philos. Mag. 1975, 31 (2), 255–274. 10.1080/14786437508228930. [DOI] [Google Scholar]
  20. Yu Y.; Yang F.; Lu X. F.; Yan Y. J.; Cho Y.-H.; Ma L.; Niu X.; Kim S.; Son Y.-W.; Feng D.; Li S.; Cheong S.; Chen X. H.; Zhang Y. Gate-Tunable Phase Transitions in Thin Flakes of 1T-TaS2. Nat. Nanotechnol. 2015, 10 (3), 270–276. 10.1038/nnano.2014.323. [DOI] [PubMed] [Google Scholar]
  21. Sipos B.; Kusmartseva A. F.; Akrap A.; Berger H.; Forro L.; Tutíš E. From Mott State to Superconductivity In-1T-TaS2. Nat. Mater. 2008, 7 (12), 960–965. 10.1038/nmat2318. [DOI] [PubMed] [Google Scholar]
  22. Yoshida M.; Zhang Y.; Ye J.; Suzuki R.; Imai Y.; Kimura S.; Fujiwara A.; Iwasa Y. Controlling Charge-Density-Wave States in Nano-Thick Crystals of 1T-TaS2. Sci. Rep. 2015, 4 (1), 7302. 10.1038/srep07302. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Wilson J. A.; Di Salvo F. J.; Mahajan S. Charge-Density Waves and Superlattices in the Metallic Layered Transition Metal Dichalcogenides. Adv. Phys. 1975, 24 (2), 117–201. 10.1080/00018737500101391. [DOI] [Google Scholar]
  24. Fazekas P.; Tosatti E. Electrical, Structural and Magnetic Properties of Pure and Doped 1T-TaS2. Philos. Mag. B 1979, 39 (3), 229–244. 10.1080/13642817908245359. [DOI] [Google Scholar]
  25. Ribak A.; Silber I.; Baines C.; Chashka K.; Salman Z.; Dagan Y.; Kanigel A. Gapless Excitations in the Ground State of 1T-TaS2. Phys. Rev. B: Condens. Matter Mater. Phys. 2017, 96 (19), 195131. 10.1103/PhysRevB.96.195131. [DOI] [Google Scholar]
  26. He W. Y.; Xu X. Y.; Chen G.; Law K. T.; Lee P. A. Spinon Fermi Surface in a Cluster Mott Insulator Model on a Triangular Lattice and Possible Application to 1T-TaS2. Phys. Rev. Lett. 2018, 121 (4), 46401. 10.1103/PhysRevLett.121.046401. [DOI] [PubMed] [Google Scholar]
  27. Wang Y. D.; Yao W. L.; Xin Z. M.; Han T. T.; Wang Z. G.; Chen L.; Cai C.; Li Y.; Zhang Y. Band Insulator to Mott Insulator Transition in 1T-TaS2. Nat. Commun. 2020, 11 (1), 4215. 10.1038/s41467-020-18040-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Svetin D.; Vaskivskyi I.; Brazovskii S.; Mihailovic D. Three-Dimensional Resistivity and Switching between Correlated Electronic States in 1T-TaS2. Sci. Rep. 2017, 7 (1), 46048. 10.1038/srep46048. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Martino E.; Pisoni A.; Ćirić L.; Arakcheeva A.; Berger H.; Akrap A.; Putzke C.; Moll P. J. W.; Batistić I.; Tutiš E.; Forró L.; Semeniuk K. Preferential Out-of-Plane Conduction and Quasi-One-Dimensional Electronic States in Layered 1T-TaS2. npj 2D Mater. Appl. 2020, 4 (1), 7. 10.1038/s41699-020-0145-z. [DOI] [Google Scholar]
  30. Park J. W.; Cho G. Y.; Lee J.; Yeom H. W. Emergent Honeycomb Network of Topological Excitations in Correlated Charge Density Wave. Nat. Commun. 2019, 10 (1), 1–7. 10.1038/s41467-019-11981-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Park J. W.; Lee J.; Yeom H. W. Zoology of Domain Walls in Quasi-2D Correlated Charge Density Wave of 1T-TaS2. npj Quantum Mater. 2021, 6 (1), 32. 10.1038/s41535-021-00330-9. [DOI] [Google Scholar]
  32. Ritschel T.; Berger H.; Geck J. Stacking-Driven Gap Formation in Layered 1 T-TaS2. Phys. Rev. B: Condens. Matter Mater. Phys. 2018, 98 (19), 1–8. 10.1103/PhysRevB.98.195134. [DOI] [Google Scholar]
  33. Lee S. H.; Goh J. S.; Cho D. Origin of the Insulating Phase and First-Order Metal-Insulator Transition in 1T-TaS2. Phys. Rev. Lett. 2019, 122 (10), 106404. 10.1103/PhysRevLett.122.106404. [DOI] [PubMed] [Google Scholar]
  34. Shin D.; Tancogne-Dejean N.; Zhang J.; Okyay M. S.; Rubio A.; Park N. Identification of the Mott Insulating Charge Density Wave State in 1T-TaS2. Phys. Rev. Lett. 2021, 126 (19), 196406. 10.1103/PhysRevLett.126.196406. [DOI] [PubMed] [Google Scholar]
  35. Tsen A. W.; Hovden R.; Wang D.; Kim Y. D.; Spoth K. A.; Liu Y.; Lu W.; Sun Y.; Hone J. C.; Kourkoutis L. F.; Kim P.; Pasupathy A. N. Structure and Control of Charge Density Waves in Two-Dimensional 1T-TaS2. Proc. Natl. Acad. Sci. U. S. A. 2015, 112 (49), 15054–15059. 10.1073/pnas.1512092112. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Liu G.; Rumyantsev S.; Bloodgood M. A.; Salguero T. T.; Balandin A. A. Low-Frequency Current Fluctuations and Sliding of the Charge Density Waves in Two-Dimensional Materials. Nano Lett. 2018, 18 (6), 3630–3636. 10.1021/acs.nanolett.8b00729. [DOI] [PubMed] [Google Scholar]
  37. Wen W.; Zhu Y.; Dang C.; Chen W.; Xie L. Raman Spectroscopic and Dynamic Electrical Investigation of Multi-State Charge-Wave-Density Phase Transitions in 1 T-TaS2. Nano Lett. 2019, 19 (3), 1805–1813. 10.1021/acs.nanolett.8b04855. [DOI] [PubMed] [Google Scholar]
  38. Zhu C.; Chen Y.; Liu F.; Zheng S.; Li X.; Chaturvedi A.; Zhou J.; Fu Q.; He Y.; Zeng Q.; Fan H. J.; Zhang H.; Liu W. J.; Yu T.; Liu Z. Light-Tunable 1T-TaS2 Charge-Density-Wave Oscillators. ACS Nano 2018, 12 (11), 11203–11210. 10.1021/acsnano.8b05756. [DOI] [PubMed] [Google Scholar]
  39. Bu K.; Zhang W.; Fei Y.; Wu Z.; Zheng Y.; Gao J.; Luo X.; Sun Y. P.; Yin Y. Possible Strain Induced Mott Gap Collapse in 1T-TaS2. Commun. Phys. 2019, 2 (1), 1–7. 10.1038/s42005-019-0247-0. [DOI] [Google Scholar]
  40. Zhao R.; Wang Y.; Deng D.; Luo X.; Lu W. J.; Sun Y. P.; Liu Z. K.; Chen L. Q.; Robinson J. Tuning Phase Transitions in 1T-TaS2via the Substrate. Nano Lett. 2017, 17 (6), 3471–3477. 10.1021/acs.nanolett.7b00418. [DOI] [PubMed] [Google Scholar]
  41. Zheng S.; Liu F.; Zhu C.; Liu Z.; Fan H. J. Room-Temperature Electrically Driven Phase Transition of Two-Dimensional 1T-TaS2 Layers. Nanoscale 2017, 9 (7), 2436–2441. 10.1039/C6NR07541J. [DOI] [PubMed] [Google Scholar]
  42. Mahajan M.; Majumdar K. Gate- and Light-Tunable Negative Differential Resistance with High Peak Current Density in 1T-TaS2 /2H-MoS2 T-Junction. ACS Nano 2020, 14 (6), 6803–6811. 10.1021/acsnano.0c00331. [DOI] [PubMed] [Google Scholar]
  43. Wang Z.; Chu L.; Li L.; Yang M.; Wang J.; Eda G.; Loh K. P. Modulating Charge Density Wave Order in a 1T-TaS2 /Black Phosphorus Heterostructure. Nano Lett. 2019, 19 (5), 2840–2849. 10.1021/acs.nanolett.8b04805. [DOI] [PubMed] [Google Scholar]
  44. Geremew A. K.; Rumyantsev S.; Debnath B.; Lake R. K.; Balandin A. A.. High-Frequency Current Oscillations in Charge-Density-Wave 1T-TaS2 Devices: Revisiting the “Narrow Band Noise” Concept. Appl. Phys. Lett. 2020, 116, 163101. 10.1063/5.0007043. [DOI] [Google Scholar]
  45. Boix-Constant C.; Mañas-Valero S.; Córdoba R.; Coronado E. van der. Waals Heterostructures Based on Atomically-Thin Superconductors. Adv. Electron. Mater. 2021, 2000987. 10.1002/aelm.202000987. [DOI] [Google Scholar]
  46. Wang L.; Meric I.; Huang P. Y.; Gao Q.; Gao Y.; Tran H.; Taniguchi T.; Watanabe K.; Campos L. M.; Muller D. a.; Guo J.; Kim P.; Hone J.; Shepard K. L.; Dean C. R. One-Dimensional Electrical Contact to a Two-Dimensional Material. Science 2013, 342 (6158), 614–617. 10.1126/science.1244358. [DOI] [PubMed] [Google Scholar]
  47. Klein D. R.; MacNeill D.; Lado J. L.; Soriano D.; Navarro-Moratalla E.; Watanabe K.; Taniguchi T.; Manni S.; Canfield P.; Fernández-Rossier J.; Jarillo-Herrero P. Probing Magnetism in 2D van der Waals Crystalline Insulators via Electron Tunneling. Science 2018, 360 (6394), 1218–1222. 10.1126/science.aar3617. [DOI] [PubMed] [Google Scholar]
  48. Thompson A. H.; Gamble R. F.; Revelli J. F. Transitions between Semiconducting and Metallic Phases in 1T-TaS2. Solid State Commun. 1971, 9 (13), 981–985. 10.1016/0038-1098(71)90444-3. [DOI] [Google Scholar]
  49. Mañas-Valero S.; Huddart B.; Lancaster T.; Coronado E.; Pratt F.. Quantum Phases and Spin Liquid Properties of 1T-TaS2. 2020, 2007.15905. arXiv. https://arxiv.org/abs/2007.15905v2 (accessed 2021/11/2).
  50. Stahl Q.; Kusch M.; Heinsch F.; Garbarino G.; Kretzschmar N.; Hanff K.; Rossnagel K.; Geck J.; Ritschel T. Collapse of Layer Dimerization in the Photo-Induced Hidden State of 1T-TaS2. Nat. Commun. 2020, 11 (1), 1247. 10.1038/s41467-020-15079-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Deng Y.; Yu Y.; Song Y.; Zhang J.; Wang N. Z.; Sun Z.; Yi Y.; Wu Y. Z.; Wu S.; Zhu J.; Wang J.; Chen X. H.; Zhang Y. Gate-Tunable Room-Temperature Ferromagnetism in Two-Dimensional Fe3GeTe2. Nature 2018, 563 (7729), 94–99. 10.1038/s41586-018-0626-9. [DOI] [PubMed] [Google Scholar]
  52. Sakabe D.; Liu Z.; Suenaga K.; Nakatsugawa K.; Tanda S. Direct Observation of Mono-Layer, Bi-Layer, and Tri-Layer Charge Density Waves in 1T-TaS2 by Transmission Electron Microscopy without a Substrate. npj Quantum Mater. 2017, 2 (1), 1–5. 10.1038/s41535-017-0025-8. [DOI] [Google Scholar]
  53. Zhu X.; Li A. J.; Stewart G. R.; Hebard A. F. Detection of Charge Density Wave Phase Transitions at 1T-TaS2 /GaAs Interfaces. Appl. Phys. Lett. 2017, 110 (18), 181603. 10.1063/1.4982964. [DOI] [Google Scholar]
  54. Kang S. D.; Snyder G. J. Charge-Transport Model for Conducting Polymers. Nat. Mater. 2017, 16 (2), 252–257. 10.1038/nmat4784. [DOI] [PubMed] [Google Scholar]
  55. Bedoya-Pinto A.; Prima-García H.; Casanova F.; Coronado E.; Hueso L. E. Spin-Polarized Hopping Transport in Magnetically Tunable Rare-Earth Quinolines. Adv. Electron. Mater. 2015, 1 (6), 1500065. 10.1002/aelm.201500065. [DOI] [Google Scholar]
  56. Mahajan M.; Murali K.; Kawatra N.; Majumdar K. Gate-Controlled Large Resistance Switching Driven by Charge-Density Wave in 1T-TaS2/2H-MoS2 Heterojunctions. Phys. Rev. Appl. 2019, 11 (2), 1. 10.1103/PhysRevApplied.11.024031. [DOI] [Google Scholar]
  57. Taychatanapat T.; Watanabe K.; Taniguchi T.; Jarillo-Herrero P. Quantum Hall Effect and Landau-Level Crossing of Dirac Fermions in Trilayer Graphene. Nat. Phys. 2011, 7 (8), 621–625. 10.1038/nphys2008. [DOI] [Google Scholar]
  58. Timrov I.; Marzari N.; Cococcioni M. Hubbard Parameters from Density-Functional Perturbation Theory. Phys. Rev. B: Condens. Matter Mater. Phys. 2018, 98 (8), 085127. 10.1103/PhysRevB.98.085127. [DOI] [Google Scholar]
  59. Giannozzi P.; Baroni S.; Bonini N.; Calandra M.; Car R.; Cavazzoni C.; Ceresoli D.; Chiarotti G. L.; Cococcioni M.; Dabo I.; Dal Corso A.; de Gironcoli S.; Fabris S.; Fratesi G.; Gebauer R.; Gerstmann U.; Gougoussis C.; Kokalj A.; Lazzeri M.; Martin-Samos L.; Marzari N.; Mauri F.; Mazzarello R.; Paolini S.; Pasquarello A.; Paulatto L.; Sbraccia C.; Scandolo S.; Sclauzero G.; Seitsonen A. P.; Smogunov A.; Umari P.; Wentzcovitch R. M. QUANTUM ESPRESSO: A Modular and Open-Source Software Project for Quantum Simulations of Materials. J. Phys.: Condens. Matter 2009, 21 (39), 395502. 10.1088/0953-8984/21/39/395502. [DOI] [PubMed] [Google Scholar]
  60. Timrov I.; Marzari N.; Cococcioni M. Self-Consistent Hubbard Parameters from Density-Functional Perturbation Theory in the Ultrasoft and Projector-Augmented Wave Formulations. Phys. Rev. B: Condens. Matter Mater. Phys. 2021, 103 (4), 045141. 10.1103/PhysRevB.103.045141. [DOI] [Google Scholar]
  61. Long G.; Henck H.; Gibertini M.; Dumcenco D.; Wang Z.; Taniguchi T.; Watanabe K.; Giannini E.; Morpurgo A. F. Persistence of Magnetism in Atomically Thin MnPS3 Crystals. Nano Lett. 2020, 20 (4), 2452–2459. 10.1021/acs.nanolett.9b05165. [DOI] [PubMed] [Google Scholar]
  62. Lejaeghere K.; Bihlmayer G.; Bjorkman T.; Blaha P.; Blugel S.; Blum V.; Caliste D.; Castelli I. E.; Clark S. J.; Dal Corso A.; de Gironcoli S.; Deutsch T.; Dewhurst J. K.; Di Marco I.; Draxl C.; Du ak M.; Eriksson O.; Flores-Livas J. A.; Garrity K. F.; Genovese L.; Giannozzi P.; Giantomassi M.; Goedecker S.; Gonze X.; Granas O.; Gross E. K. U.; Gulans A.; Gygi F.; Hamann D. R.; Hasnip P. J.; Holzwarth N. A. W.; Iu an D.; Jochym D. B.; Jollet F.; Jones D.; Kresse G.; Koepernik K.; Kucukbenli E.; Kvashnin Y. O.; Locht I. L. M.; Lubeck S.; Marsman M.; Marzari N.; Nitzsche U.; Nordstrom L.; Ozaki T.; Paulatto L.; Pickard C. J.; Poelmans W.; Probert M. I. J.; Refson K.; Richter M.; Rignanese G.-M.; Saha S.; Scheffler M.; Schlipf M.; Schwarz K.; Sharma S.; Tavazza F.; Thunstrom P.; Tkatchenko A.; Torrent M.; Vanderbilt D.; van Setten M. J.; Van Speybroeck V.; Wills J. M.; Yates J. R.; Zhang G.-X.; Cottenier S. Reproducibility in Density Functional Theory Calculations of Solids. Science 2016, 351 (6280), aad3000–aad3000. 10.1126/science.aad3000. [DOI] [PubMed] [Google Scholar]
  63. Prandini G.; Marrazzo A.; Castelli I. E.; Mounet N.; Marzari N. Precision and Efficiency in Solid-State Pseudopotential Calculations. npj Comput. Mater. 2018, 4 (1), 72. 10.1038/s41524-018-0127-2. [DOI] [Google Scholar]
  64. Dudarev S. L.; Botton G. A.; Savrasov S. Y.; Humphreys C. J.; Sutton A. P. Electron-Energy-Loss Spectra and the Structural Stability of Nickel Oxide: An LSDA+U Study. Phys. Rev. B: Condens. Matter Mater. Phys. 1998, 57 (3), 1505–1509. 10.1103/PhysRevB.57.1505. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nn1c03012_si_001.pdf (33.6MB, pdf)

Articles from ACS Nano are provided here courtesy of American Chemical Society

RESOURCES