Tensor-Based Morphometry of Fibrous Structures with Application to Human Brain White Matter

Abstract

Tensor-based morphometry (TBM) is a powerful approach for examining shape changes in anatomy both across populations and in time. Our work extends the standard TBM for quantifying local volumetric changes to establish both rich and intuitive descriptors of shape changes in fibrous structures. It leverages the data from diffusion tensor imaging to determine local spatial configuration of fibrous structures and combines this information with spatial transformations derived from image registration to quantify fibrous structure-specific changes, such as local changes in fiber length and in thickness of fiber bundles. In this paper, we describe the theoretical framework of our approach in detail and illustrate its application to study brain white matter. Our results show that additional insights can be gained with the proposed analysis.

1. Introduction

Tensor-based morphometry (TBM) is one of the most popular deformation-based approaches for analyzing anatomy. It computes, for each voxel in the image domain, the spatial derivatives of the transformations that align a set of input subject images to a template of choice. These images can be acquired from different populations, enabling cross-sectional study of anatomical differences between populations. TBM can also be applied to study longitudinal changes in anatomy by examining the transformations that match images acquired sequentially of the same subjects. The standard TBM has primarily taken advantage of the determinant of the spatial derivative matrix (known as the Jacobian matrix) [1, 2], which enables statistical mapping of local volumetric changes across populations and in time.

A well-understood weakness of using only the Jacobian determinant is that significant amount of information captured in the full matrix is being discarded. As a result, it will not be able to detect many patterns of differences that involve anisotropic changes along different spatial directions but result in no net volumetric changes. Recently, Lepore et al [3] proposed the generalized TBM as a solution to this problem. The generalized TBM extends the standard approach by applying multivariate statistics on the full deformation tensors which are derived from the Jacobian matrices and completely capture shape changes contained within them. The consistent gain in power to detect structural abnormalities makes the approach highly desirable for drug trials or computer-assisted diagnosis. However, the multivariate approach makes it difficult to interpret the detected abnormalities in anatomically intuitive terms.

In this paper, we propose a different approach for remedying the weakness of the standard TBM. The approach is specifically tailored for examining fibrous structures such as white matter and muscle. It is driven by the key observation that, for fibrous structures, the effect of transformation depends not only on the properties of the transformation itself but also on the configuration of the fibrous structure undergoing the warping. The proposed approach leverages the configuration information of the fibrous structures available from diffusion tensor imaging (DTI) and establishes both rich and intuitive descriptors of shape properties. Its ability to gain additional insights is demonstrated in an application to examine gender-related white matter differences in the aging population.

The paper is organized as follows: Section 2 describes the proposed approach in detail. Section 3 describes the application of the proposed approach to examine gender difference of white matter in the aging population. Section 4 summarizes the contribution and discusses future works.

2. Method

2.1. Tensor-Based Morphometry

In the TBM framework, given an input subject, we first establish the spatial correspondence between the subject and a template using a high-dimensional nonlinear image registration algorithm. The correspondence between the two images is captured by some diffeomorphic spatial transformation ϕ : Ω → Ω, where $\Omega \subseteq {ℝ}^n$ is the image domain (n = 2 for 2D and n = 3 for 3D). In particular, the Jacobian of the transformation, J_ϕ : x → Dϕ(x), establishes a local affine transformation model that maps the local neighborhood around a point x in the template to the corresponding neighborhood around the point ϕ(x) in the subject, such that,

$$\varphi (x+ϵ)=\varphi (x)+J_{\varphi }(x)ϵ+O\left({‖ϵ‖}^2\right),$$

with J_ϕ being a n × n matrix, the (i, j)^th entry of which is (Dϕ)_ij ≔ ∂ϕ_i/∂x_j. Beause the determinant of the Jacobian matrix J_ϕ quantifies the volume change from mapping a local neighborhood in the template to the corresponding one in the subject, a map of local volumetric change can be produced by computing this quantity at each point in the image domain [1, 2]. This approach is most commonly used in the TBM analysis, in part because the descriptive nature of the measure makes it easy to understand and to interpret. On the other hand, its inability to differentiate other patterns of shape changes that do not result in volume change has motivated active research in identifying alternative complementary measures.

2.2. Overview of the Proposed Framework

The proposed framework builds upon the standard TBM analysis by establishing a set of descriptors of shape changes that are natural and specific for fibrous structures. We observe that the fiber orientation information encoded in DTI can be leveraged to decompose the Jacobian matrix of a transformation into parts that can be interpreted in intuitive terms. This observation is illustrated in Fig. 1, which depicts, in the left panel, the local neighborhood around a point x in a DTI template, and in the right panel, the transformed version of this neighborhood using some transformation ϕ. The original neighborhood around x is represented using a shaded rectangle; its transformed version, which is centered around ϕ(x), is represented using a shaded parallelogram. The diffusion tensor at x and its warped version at ϕ(x) are shown as two lightly-shaded ellipses. The eigenvectors of each diffusion tensor form a natural local reference frame for its neighborhood: their primary eigenvectors, denoted by e₁ at x and $e_1^{\prime }$ at ϕ(x), are parallel to the orientations of the underlying fiber bundles; their secondary eigenvectors, denoted by e₂ at x and $e_2^{\prime }$ at ϕ(x), are perpendicular to the fiber orientations. The local trajectories of the underlying fiber bundles are depicted by the pairs of dashed curves, which shall not be interpreted as the fiber bundle boundaries. Observe that the effect of the Jacobian matrix J_ϕ on the transformation of the original neighborhood can be parsed into three steps: (1) rotating the rectangle such that e₁ and e₂ coincide with $e_1^{\prime }$ and $e_2^{\prime }$, respectively; (2) compressing the rectangle along $e_2^{\prime }$, and (3) shearing the rectangle along $e_1^{\prime }$. In other words, by factoring out some appropriate rotation matrix, the action of the remainder of J_ϕ can be interpreted intuitively in the local reference frame of the warped underlying fiber bundle.

Fig. 1.

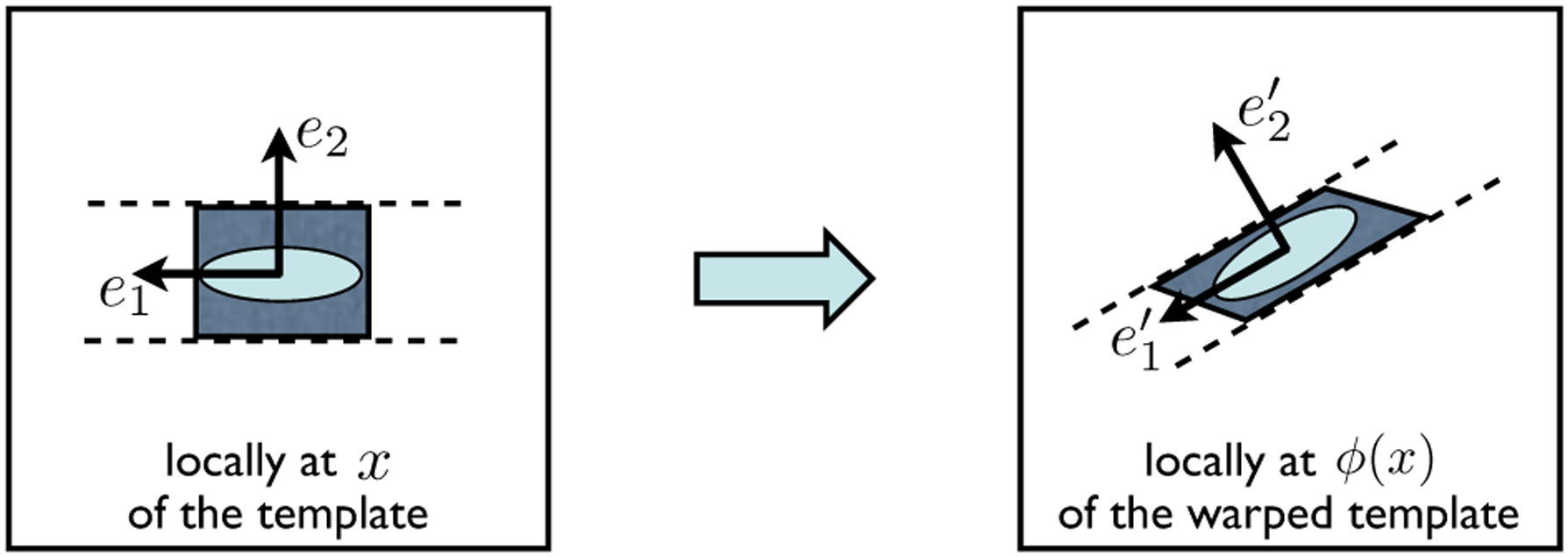
The schematic illustrates the local behavior of warping some fibrous structure with the transformation ϕ. See the main text in Section 2.2 for the details.

It turns out that this kind of decomposition of the Jacobian matrix can be done in general for fibrous structures, provided the fiber orientation information is available. In this paper, we consider the particular scenario in which the fiber orientation is derived from DTI measurements. Specifically, given the diffusion tensor D at x, its eigenvectors {e_i}_1≤i≤n, ordered in the descending order of the corresponding eigenvalues, form the basis of a natural local reference frame for the underlying fiber bundle; the rotation matrix that constitutes a change of basis from this local reference frame to the laboratory frame, which we will denote by Q, has e_i as its ith column. Similarly, the eigenvectors ${\left\{e_i^{\prime }\right\}}_{1\le i\le n}$ of the warped diffusion tensor D′ at ϕ(x) form the basis of a natural local reference frame for the warped fiber bundle; the change-of-basis matrix from this local reference frame to the laboratory frame will be denoted as Q′. The appropriate rotation matrix that matches the local reference frame of D to the one of D′ is then Q′ Q⁻¹. Therefore, we can write the Jacobian matrix as

$$J_{\varphi }=\left(Q^{\prime }R{Q}^{\prime -1}\right)\left(Q^{\prime }{Q}^{-1}\right),$$ (1)

with R denotes the remainder of J_ϕ after factoring out the rotation Q′ Q⁻¹ and being viewed in the local reference frame of D′. The following section describes the computation of R and shows that the structure of the matrix makes it particularly amenable to intuitive description of its action similar to the example given in Fig. 1.

2.3. Computation of the Residual Deformation and Its Structure

The key to computing R is in finding the tensor corresponding to the fiber bundle configuration after warping. This is known as the tensor reorientation problem, the solution to which has been established by the seminal work of Alexander et al. [4]. The authors proposed and validated a number of strategies for tensor reorientation, including the finite strain (FS) strategy and the preservation of principal direction (PPD) strategy. We choose to use the PPD strategy, summarized in Algorithm 1, because it preserves the connectivity of the underlying fiber bundle, crucial to the fidelity of warping. As illustrated in Fig. 2, the preservation of connectivity requires that the appropriate reorientation depends both on the warping transformation and the fiber configuration before warping, as done in the PPD strategy. In contrast, the FS strategy applies an identical reorientation to all tensors regardless of their fiber configurations, which evidently can disrupt fiber connectivity and thus represents only an approximation to PPD.

Fig. 2.

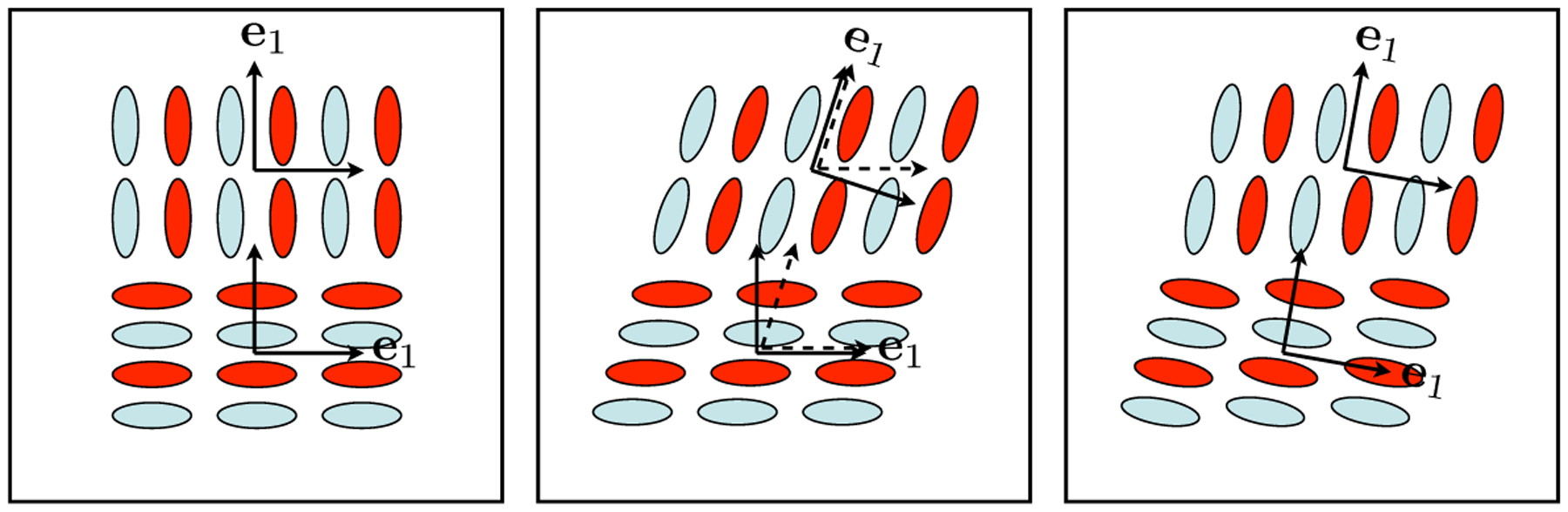
Tensor reorientation strategies for recovering correct fiber configuration after warping with a horizontal shear transformation. From left to right, the image before warping, the warped image using the PPD strategy, the warped image using the FS strategy. Observe how the original fiber connectivity, indicated with identically colored ellipses, is intact when PPD is used but is severely disrupted when FS is used.

Given our choice of the reorientation strategy, the computation of the residual deformation viewed in the local frame of the warped tensor can now be summarized in Algorithm 2, which uses Equation (1) and the fact that Q′ is orthogonal, i.e., Q′⁻¹ = Q′^T. The structure of the residual deformation is formally stated with Theorem 1.

Algorithm 1.

PPD strategy for tensor reorientation

1:	compute $e_1^{\prime }:e_1^{\prime }=J{e}_1/\Vert J{e}_1\Vert$
2:	compute $e_2^{\prime }:e_2^{\prime }=n/\Vert n\Vert$, where $n=J{e}_2-\left({\left(J{e}_2\right)}^{\text{T}}{e}_1^{\prime }\right)e_1^{\prime }$
3:	compute $e_3^{\prime }:e_3^{\prime }=e_1^{\prime }\times e_2^{\prime }$

Algorithm 2.

Compute the residual deformation R at a point x

1:	compute the Jacobian matrix J at x
2:	compute the matrix Q = (e1, e2, e3) with {ei}1≤i≤3 being the eigenvectors of the diffusion tensor D at x ordered in the descending order of the corresponding eigenvalues
3:	compute the matrix $Q^{\prime }=\left(e_1^{\prime },e_2^{\prime },e_3^{\prime }\right)$ with ${\left\{e_i^{\prime }\right\}}_{1\le i\le 3}$ being derived from J and {ei}1≤i≤3 using the PPD strategy
4:	compute the matrix R = Q′TJQ

Theorem 1.The residual deformation R, computed usingAlgorithm 2, is an upper-triangular matrix with positive diagonal entries.

Proof. First, we simplify and rewrite Equation (1) as

$$JQ=Q^{\prime }R.$$ (2)

Recall that, by defintion, Q = (e₁, e₂, e₃). Hence we have JQ = (Je₁, Je₂, Je₃). Here we use a different formulation of the PPD strategy that was pointed out by Cao et al [5]. They recognized that the PPD strategy, as described in Algorithm 1, is in fact equivalent to the application of the Gram-Schmidt orthonormalization procedure, which produces an orthonormal basis from a non-orthogonal but linearly-independent basis. In this case, the non-orthogonal but linearly-independent basis is composed of the vectors $J{e}_1$, $J{e}_2$, and $J{e}_3$. The orthonormal basis that the Gram-Schmidt procedure generates from this basis consists of precisely the vectors $e_1^{\prime }$, $e_2^{\prime }$, and $e_3^{\prime }$. The procedure is summarized in Algorithm 3; its equivalence to Algorithm 1 can be readily verified.

Algorithm 3.

Gram-Schmidt procedure applied to $J{e}_1$, $J{e}_2$, and $J{e}_3$

1:	Initialize $v_i=J{e}_i$ for 1 ≤ i ≤ 3
2:	compute u1: u1 = vl
3:	compute $u_2:u_2=v_2-{\text{proj}}_{u_1}{v}_2$, where projab = (aTb)a/(aTa)
4:	compute $u_3:u_3=v_3-{\text{proj}}_{u_1}{v}_3-{\text{proj}}_{u_2}{v}_3$
5:	compute $e_1^{\prime }$, $e_2^{\prime }$, and $e_3^{\prime }:e_1^{\prime }=u_1/\Vert u_1\Vert$, $e_2^{\prime }=u_2/\Vert u_2\Vert$, and $e_3^{\prime }=u_3/\Vert u_3\Vert$

The equivalence of Algorithms 1 and 3 is important because the Gram-Schmidt procedure can be further viewed as the QR-decomposition of matrices which uniquely decompose any invertible matrix A into an orthogonal matrix Q_A and an upper triangular matrix R_A with positive diagonal entries such that A = Q_AR_A (See [6] for a proof). In particular, the column vectors of the orthogonal matrix Q_A are computed from applying the Gram-Schmidt procedure to the column vectors of the matrix A. In our case, JQ is the matrix to be decomposed with the QR-decomposition procedure. The matrix is clearly invertible since J is the Jacobian matrix of a diffeomorphic transformation and Q is an orthogonal matrix. By definition, Q′, whose column vectors are $e_1^{\prime }$, $e_2^{\prime }$, and $e_3^{\prime }$, is precisely the orthogonal matrix computed from the QR-decomposition of JQ. From Equation (2) and the uniqueness of the QR-decomposition, it is evident that R is the upper-triangluar matrix with positive diagonal entries. □

An additional property of the proposed decomposition can be seen by rewriting Equation (1) as

$$J_{\varphi }=\left(Q^{\prime }{Q}^{-1}\right)\left(QR{Q}^{-1}\right),$$

which reads that the effect of J_ϕ can also be seen as first applying the same residual deformation but viewed in the local reference frame of D, then applying the same rotation Q′ Q⁻¹. In other words, the order in which the residual deformation and the rotation are applied does not change the output.

2.4. Intuitive Descriptors for White Matter Morphometry

To derive intuitive descriptors for white matter morphometry, we first observe that, in white matter, the primary eigenvector, e₁, has been shown to provide a good estimate to the orientation of the underlying axon fiber bundle [7]. On the other hand, the secondary and the tertiary eigenvectors, e₂ and e₃, can not be determined consistently or can be of any two orthogonal unit vectors lying in the plane perpendicular to e₁, because the secondary and tertiary eigenvalues are often very close to one another or can not be consistently differentiated due to noise. In this scenario, the residual deformation will take the following more general form:

$$R=\left(\begin{array}{cc}{s}_1& V^{\text{T}}\\ 0& S_{23}\end{array}\right),$$

where V is a 2-dimensional vector and S₂₃ is a 2-by-2 matrix. It can be viewed as the QR-decomposition with the basis formed by e₁ and the subspace orthogonal to it, spanned by e₂ and e₃. Because det R = s₁ × det(S₂₃), the structure of R enables us to decompose the determinant of Jacobian, det J = det R, into two components, s₁ and det S₂₃. s₁ measures local changes along the eigenvector e₁, i.e., elongation or compression along the fiber bundle; det S₂₃, referred to as s₂₃ hereafter, measures local changes orthogonal to e₁, i.e., expansion or shrinkage in the cross-sectional area of the fiber bundle.

3. Application

To demonstrate the utility of the proposed analysis, we applied the analysis to study gender difference of white matter in the aging population. The subjects used in the present study were extracted from the IXI brain database (http://www.ixi.org.uk) developed jointly by Imperial College of Science Technology & Medicine and University College London. The IXI database consists of brain MR images from 550 normal subjects between the age of 20 and 80 years acquired at three sites and freely available for downloads. We selected a total of 35 subjects (16 males and 19 females) with the following criteria: 65 years or older, scanned at the same site, and with available DTI data of sufficient quality. To spatially normalize the data, we applied the approach described in [8] which simultaneously constructs a population-specific DTI template from the subject data and normalizes the subjects to the resulting template. The approach is based on high-dimensional tensor-based image registration and has been shown to outperform scalar-based registration.

After normalization, we applied both the standard TBM and the proposed approach to the Jacobian matrix fields computed from the spatial transformations mapping the subjects to the template. The standard voxel-based statistical mapping on the whole-brain white matter was then computed for the Jacobian determinant map, the maps of the two proposed descriptors. The white matter region is defined as the voxels with fractional anisotropy above 0.2. The voxels with significant differences between the gender groups were determined after FDR-based multiple comparison correction at the significance level p_FDR < 0.05.

The results are shown in Fig. 3, which clearly demonstrates that additional insights can be gained with the proposed approach. The two signifcant clusters were identified with the standard TBM approach, shown on slice 49 and 75 respectively. The cluster on the slice 75 co-localizes with one of the clusters of s₁, suggesting that local volumetric change at the location can be attributed to local change along the fiber bundle. On the other hand, the cluster on the slice 49 co-localizes with one of the clusters of s₂₃, indicating that local volumetric change at the location can be attributed to local change in the cross-sectional area of the fiber bundle. Furthermore, additional clusters, such as the examples on the slices 82 and 88, were identified by s₁ and s₂₃. These group differences were otherwise not detected by the standard TBM alone.

Fig. 3.

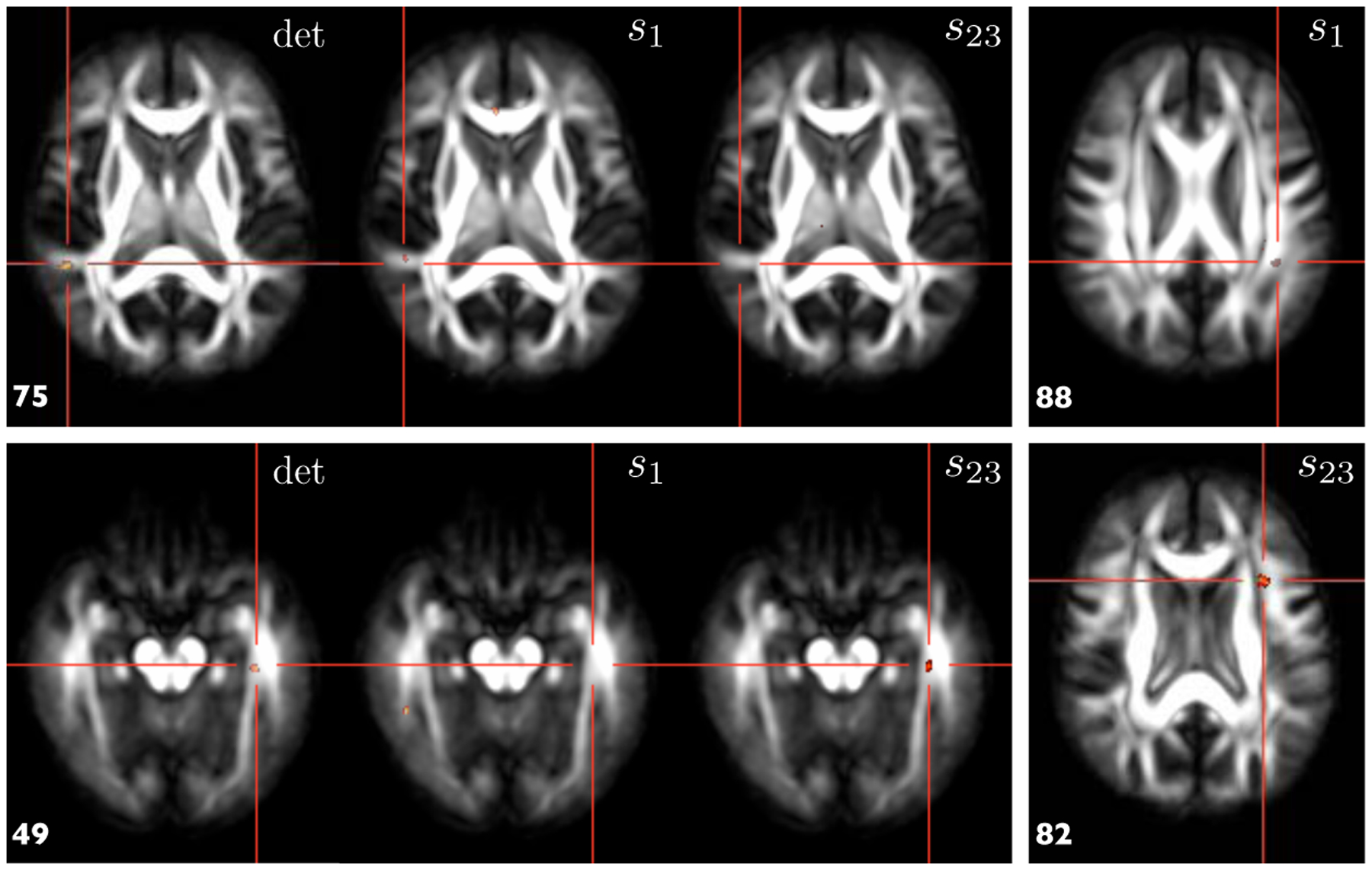
Results of the voxel-based statistical mappings on the Jacobian determinant (det), s₁ and s₂₃. See Sec. 3 for the details

4. Discussion

In summary, we have described a new approach for TBM tailored specifically for examining fibrous structures. The approach derives the information on fibrous structure configuration from DTI data and combines it with the transformations computed from image registration to elucidate shape and orientational changes specific to fibrous structures. The resulting descriptors are highly intuitive and specific. We note that additional orientational descriptors can also be determined from the rotation matrix Q′ Q⁻¹, e.g., $e_1^{\text{T}}{e}_1^{\prime }$ which measures the angle between e₁ and $e_1^{\prime }$. Future works will examine the application of such orientational descriptors and apply this new theorectical framework to study cardiac laminar structures.