Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2021 Aug 30;21(18):7617–7624. doi: 10.1021/acs.nanolett.1c02237

Squeeze-Film Effect on Atomically Thin Resonators in the High-Pressure Limit

Robin J Dolleman †,‡, Debadi Chakraborty ‡, Daniel R Ladiges ‡,§, Herre S J van der Zant †, John E Sader ‡, Peter G Steeneken †,∥,*
PMCID: PMC8461654  PMID: 34461013

Abstract

graphic file with name nl1c02237_0007.jpg

The resonance frequency of membranes depends on the gas pressure due to the squeeze-film effect, induced by the compression of a thin gas film that is trapped underneath the resonator by the high-frequency motion. This effect is particularly large in low-mass graphene membranes, which makes them promising candidates for pressure-sensing applications. Here, we study the squeeze-film effect in single-layer graphene resonators and find that their resonance frequency is lower than expected from models assuming ideal compression. To understand this deviation, we perform Boltzmann and continuum finite-element simulations and propose an improved model that includes the effects of gas leakage and can account for the observed pressure dependence of the resonance frequency. Thus, this work provides further understanding of the squeeze-film effect and provides further directions into optimizing the design of squeeze-film pressure sensors from 2D materials.

Keywords: graphene, nanoelectromechanical systems (NEMS), pressure sensor, gas damping

The hexagonal structure of graphene gives rise to unique electronic properties, which has attracted considerable interest in the scientific community.1 Moreover, the strong bonds between the carbon atoms make this material one of the strongest materials ever measured.2,3 These properties, in combination with a low mass per area, high flexibility, and gas impermeability, make graphene an interesting material for sensing applications.4−19 Graphene pressure sensors using the squeeze-film effect promise high responsivity, while at the same time considerably reducing the sensor area compared to state-of-the art sensors.9,10 Squeeze-film pressure sensors compress a gas in a shallow cavity underneath the vibrating membrane, which raises the stiffness of the system by an amount that depends on the gas pressure.20−27 If the membrane vibrates at sufficiently high frequencies and if the compression is isothermal, then the resonance frequency, ω, of the graphene membrane has a pressure dependence that can be described by10

graphic file with name nl1c02237_m001.jpg 1

where ω0 is the mechanical resonance frequency in vacuum, p is the ambient gas pressure, g0 is the distance between the moving membrane and the fixed substrate, and ρh is the membrane’s mass per square meter. Due to the ultralow ρh of single-layer graphene, large shifts in frequency ω can be expected from eq 1. Although eq 1 describes the pressure dependence of the resonance frequency at low pressures well, significant deviations from this equation are observed at pressures above 100 mbar, which are presently not understood.10 To clarify these observations, a more in-depth understanding of the squeeze-film effect in these nanoscale systems is required.

Here, we study the squeeze-film effect on single-layer graphene membrane resonators as a function of pressure for different types of gases. A clear, gas-dependent, deviation of the frequency response from the behavior predicted by eq 1 is found in the 100–1000 mbar pressure range. Both the experiments and simulations show that the onset of the deviation is correlated to the quality factor of the resonance, which can be accounted for by the gas leakage out of the gap region with a rate that is characterized by a single relaxation time. This work therefore provides a deeper understanding on squeeze-film dynamics and its effect on atomically thin membranes. The results can contribute to improving the operation and design of squeeze-film pressure sensors.

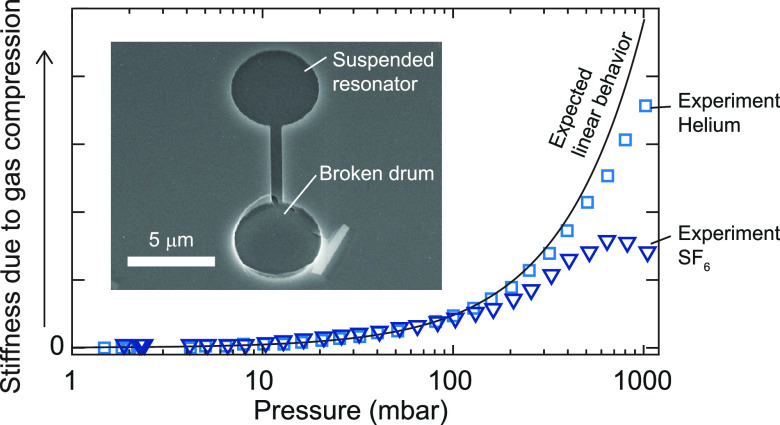
The samples consist of suspended single-layer graphene grown by chemical vapor deposition which are suspended over a dumbbell shaped cavity (Figure 1a,c,d) and of which the graphene over one-half of the dumbbell is broken. Since the other half of the graphene dumbbell remains intact, a venting channel is created toward the environment, and this prevents pressure differences from forming across the membrane’s surface, thus preventing resonance frequency shifts due to pressure-induced membrane tension.4,7,10 The venting channel therefore ensures that any frequency shift can be attributed to the squeeze-film effect. The fabrication process to produce these samples is identical to that reported in several previous works28−32 and described in more detail in Supporting Information section S1. The sample is mounted in a chamber which can contain different gases at a controlled pressure. The membrane is opto-thermally actuated, and its motion is read out using the optical setup shown in Figure 1b. By fitting a damped harmonic oscillator model to the frequency responses, the natural resonance frequency and the quality factor is extracted as a function of pressure (Figure 1e,f). More details regarding the samples, experimental setup, and data analysis can be found in the Supporting Information S1.

Figure 1.

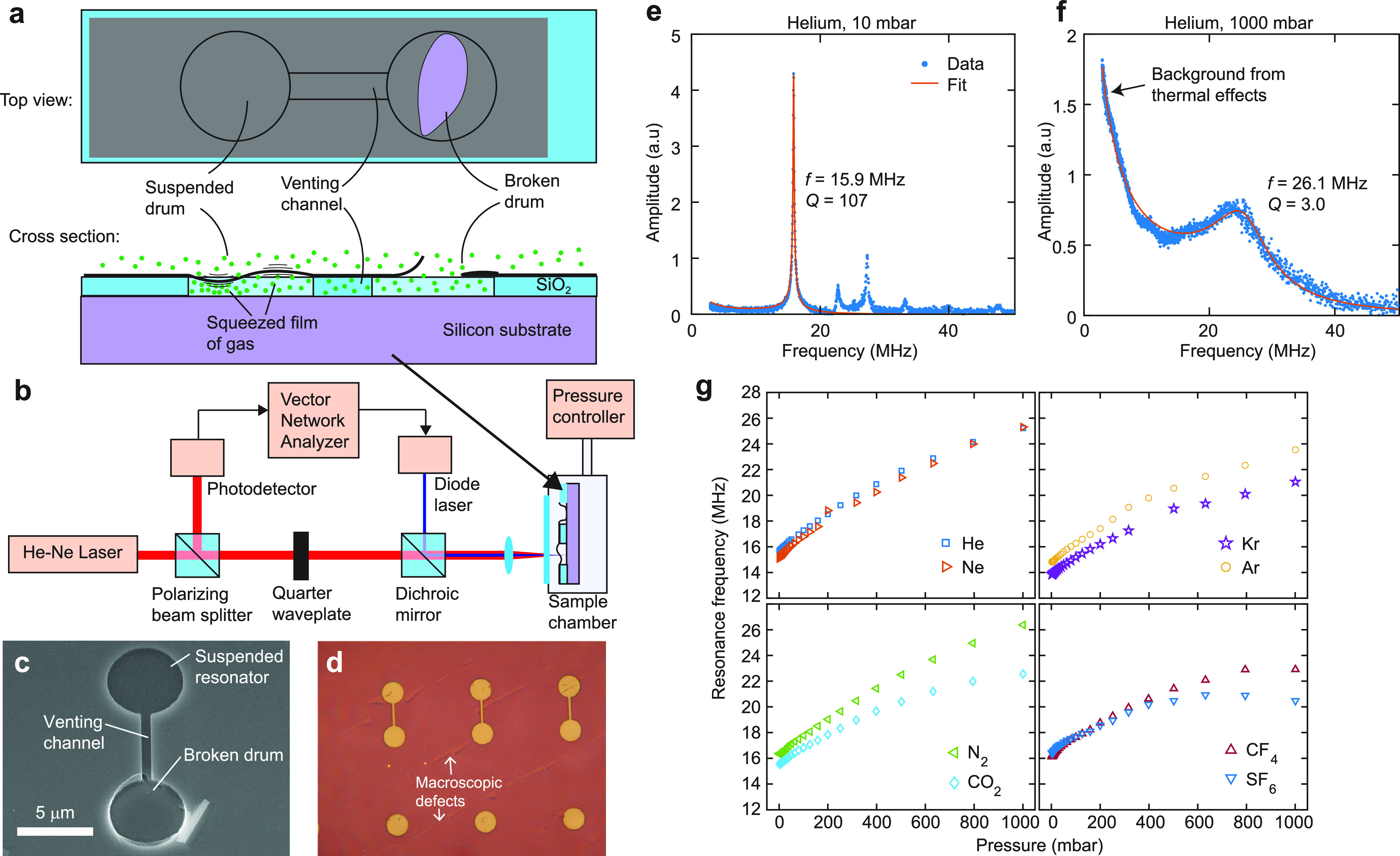
Figure 1

Open in a new tab

Graphene samples used in the experiment and the experimental setup to actuate and detect their motion. (a) Top view and cross-sectional view of a graphene resonator on a dumbbell-shaped cavity. The cross-sectional view shows a schematic drawing of the resonator’s motion, highlighting where compression of the gas occurs due to the squeeze-film effect. (b) Interferometric setup used to actuate and detect the motion. (c) Scanning electron microscopy image of a representative device used in this study. The bottom half of the dumbbell is broken, while the top half is whole. (d) Optical microscopy image of a part of the chip, showing the coverage of graphene over the chip’s surface and the macroscopic defects which helps one part of the dumbbell to break. (e) Measured amplitude of motion for a 5 μm diameter membrane as a function of frequency in a 10 mbar helium environment, and a fit (red lines) to the first resonance peak and the low-frequency background using the procedure described in Supporting Information section S1. The measured amplitude is corrected for any delays in the electronic components of the experimental setup. (f) Same as (e), but at a higher pressure of 1000 mbar. The background at low frequencies originates due to thermal effects, as explained in Supporting Information section S1. (g) Pressure-dependent resonance frequency for 8 different gases measured on a 5 μm diameter drum.

Figure 1g shows the pressure-dependent resonance frequency for 8 different gases on a 5 μm diameter drum. For all gases, the resonance frequency increases as a function of pressure due to the squeeze-film effect. It is observed that the total frequency shift depends on the type of gas: gases with a high molecular mass such as CF4 and SF6 show a lower shift than gases with a low molecular mass such as He and Ne. Furthermore, while most gases show a monotonic increase of the resonance frequency with pressure, SF6 also shows a decrease in resonance frequency at high pressures. Both the gas dependence and the decrease in resonance frequency are not in agreement with eq 1, and we will study this in more detail.

Since the vacuum resonance frequency (ω0) can change up to 20% between consecutive measurements (Figure 1g), it is convenient to rescale the measured resonance frequency as a function of pressure. We therefore define a dimensionless squeeze-film stiffness Δ that rescales the measured pressure-dependent resonance frequency ω, based on eq 1:

graphic file with name nl1c02237_m002.jpg 2

where pref is a reference pressure chosen to be 1000 mbar, ρh for single-layer graphene is 7.70 × 10–7 kg/m2, and g0 is measured to be 300 nm. This dimensionless stiffness Δ allows us to compare the squeeze-film effect for different measurements, even when the vacuum resonance frequency of the resonator has shifted.

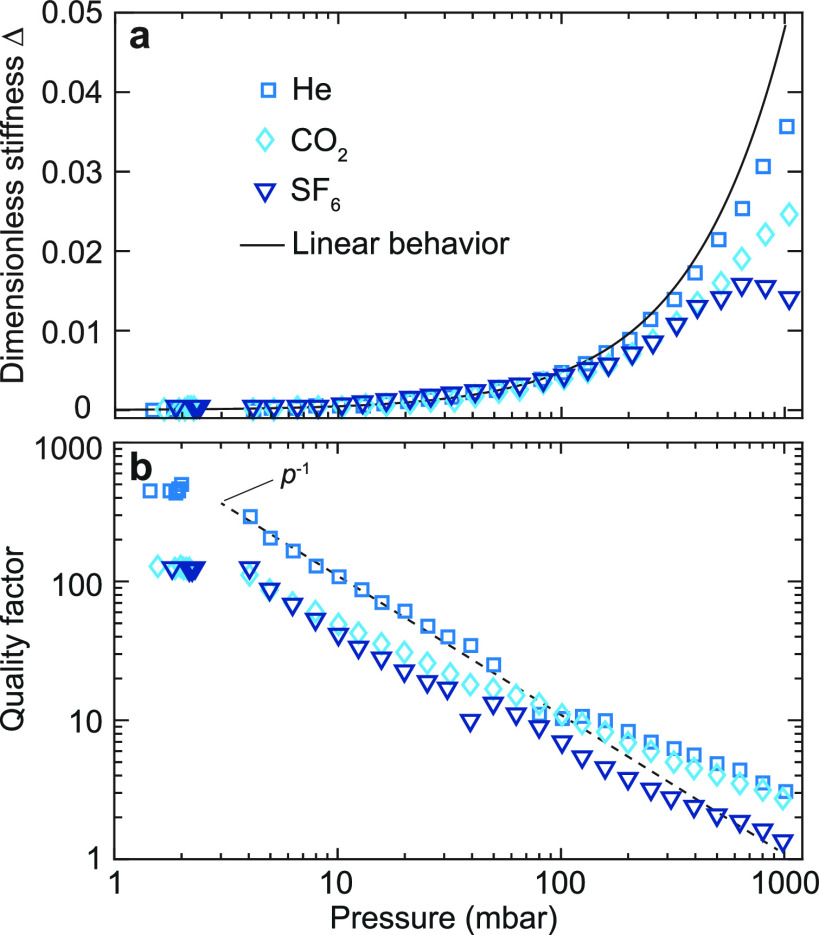
Figure 2a shows the measured dimensionless squeeze-film stiffness Δ as a function of pressure for three different gases from the same drum as Figure 1g; the results on 5 other gases are shown in the Supporting Information S2. To analyze the deviations from the linear behavior in Figure 2a, we fit a polynomial to the Δ of helium, Δ = A1p + A2p2 + ..., where the order is increased until we obtain a reasonable fit in the whole pressure range. In this case, the fit was made using a second order polynomial. For the squeeze-film effect in the ideal case, meaning described well by eq 1, we expect that 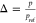Inline graphic. However, since the mass of the single-layer graphene can deviate significantly from theory33,34 and is unknown to us, we assume that in the ideal case Δ scales linearly with pressure p. This behavior is represented by the black line in Figure 2a, where we only plot Δlin = A1p. For all the gases in Figure 2a, we observe that Δ is similar up to 100 mbar and described well by this linear behavior. However, at higher pressures, a significant gas dependence of Δ is observed, and all gases show a lower stiffness than expected. We do not find significant gas-dependence in the linear part of the squeeze-film stiffness (see Supporting Information section S6). This confirms our notion that the gas compression is well-approximated as isothermal, because in the adiabatic case the stiffness would depend on the number of degrees of freedom of the gas particles.22 Furthermore, this rules out that the observed frequency shift can be attributed to mass loading from the potential flow of the gas on the top surface.

Figure 2.

Figure 2

Open in a new tab

Measured squeeze-film stiffness and quality factor as a function of pressure and gas for a 5 μm diameter single-layer graphene drum. (a) Dimensionless stiffness Δ as function of gas pressure for 3 different gases. The linear behavior line in both figures is obtained by fitting a polynomial to the helium response and plotting only the linear part. (b) Quality factor of the fundamental resonance as a function of pressure for 3 different gases. The dashed line shows Q ∝ p–1 at low pressures.

The quality factor as a function of gas pressure is shown in Figure 2b. For all gases, the quality factor decreases as a function of pressure due to friction with the gas, with a similar slope on a logarithmic scale. Throughout the pressure range studied here, low-density gases tend to show less dissipation than high-density gases. At any pressure, the quality factor changes with less than an order of magnitude as a function of the molecular weight of the gases. In the 40–100 mbar pressure range, deviations can be observed in the quality factor, which can be attributed due to imprecisions arising from the fitting, since the amplitude in this pressure range is low (see Supporting Information section S1). At low pressures, we find that Q ∝ p–1, as expected for the free molecular regime.35 At high pressures, however, the quality factor is higher than this trend which is in agreement with other works that show the same effect at higher pressures.10,35

To examine the cause of the reduced stiffness at high pressures, we compare the experimental results to several dimensional numbers describing the properties of the fluid flow or the mechanics of the resonator. For each gas, we define the dimensionless stiffness deviation as Δdev = Δ – Δlin. The dimensionless stiffness deviation is then compared to other dimensionless numbers: first, the quality factor of resonance, and second, the Reynolds number, that gives the ratio between inertial and viscous forces. For an oscillating flow, this is defined as21

graphic file with name nl1c02237_m004.jpg 3

where ρg is the density of the gas and μ is the viscosity. The third dimensionless number is the Knudsen number, which characterizes the degree of gas rarefaction and is defined as

graphic file with name nl1c02237_m005.jpg 4

where λ is the mean free path of the molecules of the gas. The fourth dimensionless squeeze number is defined by Blech:21,36

graphic file with name nl1c02237_m006.jpg 5

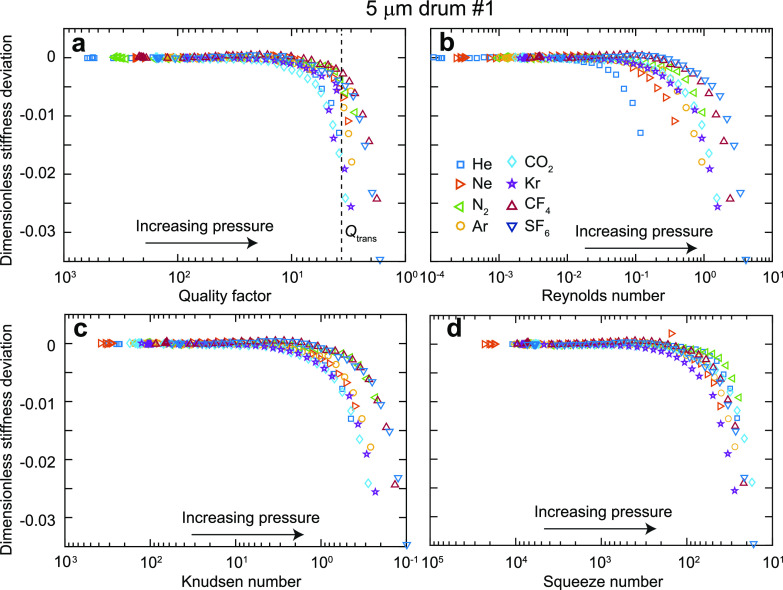
Figure 3 shows the result of the analysis for a 5-μm diameter drum for all eight gases used in this study. Additional data sets with different drums are shown in the Supporting Information S2. For easier comparison, the horizontal axis of the quality factor, Knudsen number, and squeeze number are reciprocal such that the left-hand side of the graph corresponds to low pressure and the right-hand side corresponds to high pressure. In all graphs, the stiffness deviation is initially zero and then goes toward negative values; this corresponds to the deviations from the linear behavior discussed above.

Figure 3.

Figure 3

Open in a new tab

Stiffness deviation as a function of dimensionless parameters. (a) Dimensionless stiffness deviation measured on a 5-μm diameter drum as a function of quality factor for 8 different gases, (b) as a function of Reynolds number, (c) as a function of Knudsen number, and (d) as a function of squeeze number.

To identify the main parameter that determines the deviation from linear behavior, we compare the values of Q, Re, Kn, and Sq at a value of Δdev,trans = −0.005. This represents a significant deviation from linear behavior that exceeds experimental uncertainties. Although the exact parameter choice for Δdev,trans will affect the quantitative values, it will not affect the qualitative conclusions and comparison. Determining the transition point for each gas and each drum used in this study (including those presented in the Supporting Information S2), we find that the transition occurs at Q = 3.81 ± 1.07, Re = 0.55 ± 0.38, Kn = 0.82 ± 0.55, and Sq = 94.3 ± 71.7 where the error bars represent the standard deviation. The relative standard deviations σ for each parameter are σQ = 28%, σRe = 50%, σKn = 69%, and σSq = 76%. This analysis shows that transition point where the stiffness deviates from the ideal linear behavior is thus most strongly associated with a certain number of the quality factor (Qtrans ≈ 3.8), since this shows the smallest relative spread compared to the Reynolds, Knudsen, and squeeze numbers.

The experimental analysis reveals that eq 1 is no longer valid when the quality factor is lower than approximately 3.8. However, due to experimental uncertainties, we cannot fully rule out that this effect still originates from transitions in the fluid flow characterized by the Reynolds, Knudsen, or squeeze number. Therefore, we use simulations using two approaches and analyze them in a manner similar to that used for the experimental data. The first approach employs finite element simulations by solving the compressible unsteady Stokes equation for the gas together with Navier’s equation for the solid membrane using the eigenfrequency solver of COMSOL Multiphysics.37,38 An axisymmetric slice of the drum is considered in this continuum model (see Supporting Information section S3). No-slip boundaries were implemented on the solid surfaces. The second approach includes the effects of gas rarefaction by simulating the system using the frequency-domain Monte Carlo Method.39,40 This approach solves the Boltzmann Transport Equation (BTE), and should therefore provide more accurate results for low gas pressures. The simulations are benchmarked against a previously published data set10 from a 5 μm diameter drum from 31-layer graphene over a 400 nm deep cavity, which is shown in the Supporting Information section S3. While both the BTE and continuum simulations show the experimentally observed deviations in the stiffness, the BTE simulations are computationally expensive at high pressures. We therefore choose to perform the comparison to the dimensionless numbers with different gases on the continuum simulations only in regions where the Knudsen number is smaller than 1. For the BTE simulations, we only performed simulations on He, CO2, and SF6 below 200 mbar for this analysis.

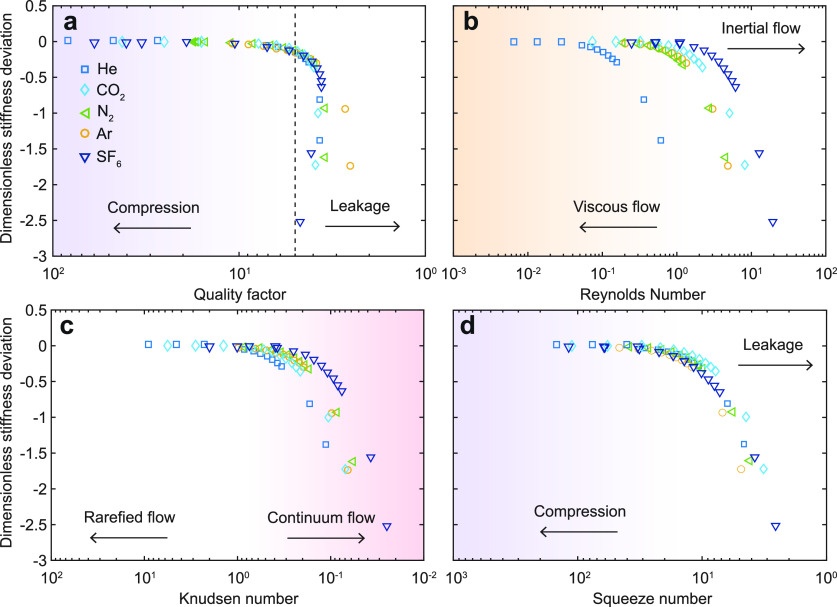
The analysis on the simulated data is shown in Figure 4. This reveals that there is a single quality factor of Q ≈ 5 where the transition takes place indicated by the dashed line in Figure 4. The simulations also show that the point Δdev = −0.005 is not at the same Reynolds or Knudsen number, confirming that the Q-factor is the strongest correlated to the point beyond which deviations from eq 1 start to increase. Comparing the dimensionless stiffness deviation shift to the case of the 5 μm diameter drum in the experiments (Figure 3), the deviations found in the simulation are similar to those of a function of Reynolds and Knudsen numbers, with transitions taking place in similar ranges. However, we observe a much smaller spread in the squeeze number in the simulations compared to the experimental data; this may be attributed to slip-flow effects in the experiment that alter the degree of squeezing of the gas, since these slip flow effect are not included in the model.

Figure 4.

Figure 4

Open in a new tab

Simulated dimensionless stiffness deviation as a function of (a) the mechanical quality factor, (b) the Reynolds number, (c) the Knudsen number, and (d) the squeeze number.

The experiments and simulations thus both show a smaller squeeze-film stiffness effect compared to eq 1, and the transition is point is associated with a certain value of the quality factor. To investigate why this happens, we constructed a simple 1D model for the motion of the membrane in the frequency domain:

graphic file with name nl1c02237_m007.jpg 6

where β is a proportionality constant and the change in gas pressure Δp is related to the displacement x as17

graphic file with name nl1c02237_m008.jpg 7

where γ is another proportionality constant. This equation is equivalent to the linearized Reynolds equation,21 where the lateral position dependence of the pressure has been projected onto one generalized coordinate Δp. The relaxation of Δp after the membrane compresses the gas is approximated with a single characteristic leak time constant τg. A similar approach has been taken in the free molecular regime, where τg is the random walk diffusion time.41 Solving this coupled system (eqs 6 and 7) gives complex eigenvalues (see Supporting Information section S4):

graphic file with name nl1c02237_m009.jpg 8

where σ = τgω is a dimensionless number describing the compression of the gas, which compares the time scale of compression 1/ω to the pressure relaxation time τg. For σ ≫ 1, eq 8 becomes equal to eq 1. However, for lower values of σ, the resonance frequency (as determined by the real part of eq 8) becomes smaller than that in eq 1. Using that the quality factor 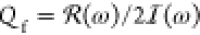Inline graphic, we find (see Supporting Information section S4):

graphic file with name nl1c02237_m011.jpg 9

where

graphic file with name nl1c02237_m012.jpg 10

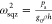where Inline graphic. The quality factor thus depends on two dimensionless numbers: the dimensionless number σ and the relative shift in resonance frequency ωsqz/ω0.

Equation 8 predicts a relation between the stiffness and damping due to the squeeze-film effect for a certain fixed σ. To verify this relation, we define the relative stiffness deviation, which can be related to the dimensionless number σ as shown in the Supporting Information section S5:

graphic file with name nl1c02237_m014.jpg 11

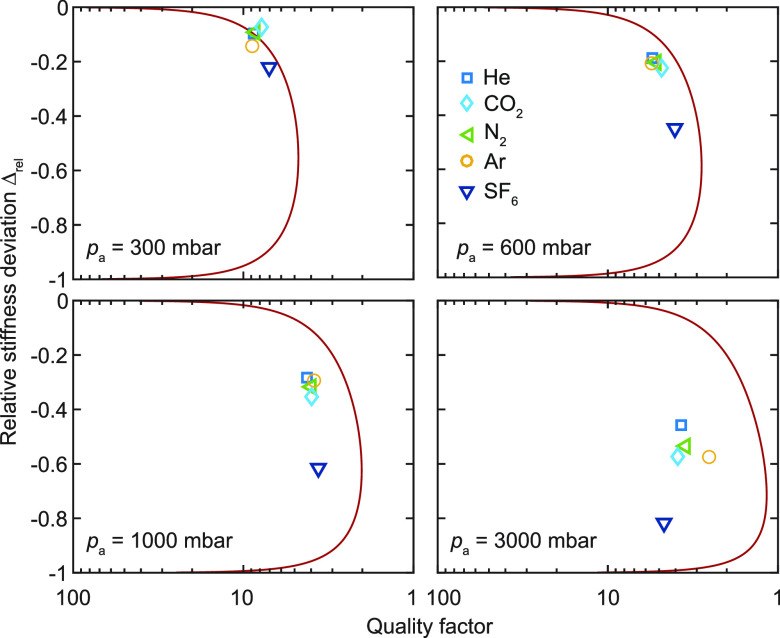
This equation is inverted to obtain σ and then substituted into eqs 9 and 10, which results in a relationship between the quality factor Qf and relative stiffness deviation Δrel where the only free parameter is the pressure pa (assuming ρh and g0 are known). Figure 5 shows this relationship at fixed pressures compared to the results of the continuum simulation. The trend predicted by eqs 9–11 is in qualitative agreement with the results from the continuum simulation at pressures of 300 and 600 mbar. However, at 1000 and 3000 mbar, the single relaxation time model predicts lower quality factors than those obtained by the continuum model. The simplifications behind the single relaxation time model may account for this difference, since the continuum model can take multiple time scales into account. The relation between Δrel and the quality factor revealed in Figure 5 explains why the stiffness deviations are more strongly correlated to the quality factor of resonance instead of the dimensionless numbers describing the fluid flow.

Figure 5.

Figure 5

Open in a new tab

Relative stiffness deviation (eq 11) versus the quality factor from the continuum model. The red lines are predictions at fixed pressures obtained from the single relaxation time models from eq 8.

From the model, we conclude that the cause of the deviations from eq 1 is the effect of gas leakage, leading to relaxation times that are not long enough compared to the period of oscillation to be neglected. These effects modify the dimensionless number σ and reduce the resonance frequency with respect to eq 1. This reduced responsivity can be mitigated by either increasing the resonance frequency or the leak time constant τg. One approach to achieve a higher resonance frequency may be to clean the graphene membrane to reduce the mass. In Supporting Information section S3, we show both continuum and BTE simulation results for a helium atmosphere in the case of clean single-layer graphene (with a mass of 7.70 × 10–7 kg/m2) and a 31-layer device in nitrogen, presented in ref (10). These simulations suggest that if the graphene is cleaned in order to reduce the mass that the responsivity of the squeeze-film pressure sensors will significantly improve. We attempted to clean the single-layer graphene in this study by argon annealing at 400 °C; however, this resulted in destruction of the drums.

In the future, eq 8 can be used instead of eq 1 to understand the effects of gas leakage on the responsivity of squeeze-film pressure sensors. Furthermore, we find that in 2D materials the quality factor of resonance is a better indication of these leakage effects than the dimensionless squeeze number, which can be attributed to the onset of slip-flow effects in the near-continuum regime where these sensors operate. Their behavior crucially depends on the exact value of τg, which is determined by the exact geometry of the device17 and the properties of the gas flow. Therefore, the simulations on a device level, such as the continuum and BTE simulations presented in this work, are crucial to understand the behavior of these sensors.

In conclusion, we studied the squeeze-film effect in single-layer graphene resonators in different gases and found a lower resonance frequency than expected. By examining the experiments and simulations of the device, we find that the transition toward this lower resonance frequency regime is correlated to the quality factor of the resonance. We explain this by a one-dimensional mechanical model and show that this is related to a low value of the dimensionless number σ. This suggests that to improve future squeeze-film pressure sensors from graphene the resonance frequency and the leak time constant need to be increased. The experiments and simulations thus provide an improved understanding into the fluid-structure interaction at the nanoscale and provides a means to better engineer future sensors from suspended 2D materials.

Acknowledgments

The authors thank Applied Nanolayers B.V. for the supply and transfer of the single-layer graphene used in this study. This work is part of the research programme Integrated Graphene Pressure Sensors (IGPS) with project number 13307 which is financed by The Netherlands Organisation for Scientific Research (NWO). The research leading to these results also received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 785219 and 881603 Graphene Flagship. This work has received funding from the EMPIR programme cofinanced by the Participating States and from the European Union’s Horizon 2020 research and innovation programme. R.J.D. also acknowledges funding from the Mobility Grant within the European Union’s Horizon 2020 research and innovation programme under grant agreement No 785219 Graphene Flagship, and support from the University of Melbourne and the Graduate Union of the University of Melbourne, Inc. D.C., D.R.L., and J.E.S. gratefully acknowledge support from the Australian Research Council Centre of Excellence in Exciton Science (CE170100026) and the Australian Research Council Grants Scheme. D.R.L. also acknowledges funding from the US Department of Energy, Office of Science, Office of Advanced Scientific Computing Research, Applied Mathematics Program under Contract No. DE-AC02-05CH11231.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.nanolett.1c02237.

  • Details on the fabrication, experimental setup, and data analysis; additional references; remainder of the data in Figure 2; the resonance frequency and Q factor of six more samples and their stiffness deviation as a function of dimensionless numbers; further details on the numerical simulations; derivation of the relation between the Q factor and the dimensionless number σ (eqs 9 and 10); further derivation of the relation between the relative stiffness deviation (eq 11) and the Q factor; comparison of the linear stiffness slopes between the different gases to rule out adiabatic compression and potential flow effects (PDF)

Author Present Address

# Second Institute of Physics, RWTH Aachen University, 52074, Aachen, Germany

The authors declare no competing financial interest.

Supplementary Material

nl1c02237_si_001.pdf (1.9MB, pdf)

References

  1. Geim A. K.; Novoselov K. S. The rise of graphene. Nat. Mater. 2007, 6, 183–191. 10.1038/nmat1849. [DOI] [PubMed] [Google Scholar]
  2. Lee C.; Wei X.; Kysar J. W.; Hone J. Measurement of the elastic properties and intrinsic strength of monolayer graphene. Science 2008, 321, 385–388. 10.1126/science.1157996. [DOI] [PubMed] [Google Scholar]
  3. Wang L.; Williams C. M.; Boutilier M. S. H.; Kidambi P. R.; Karnik R. Single-layer graphene membranes withstand ultrahigh applied pressure. Nano Lett. 2017, 17, 3081–3088. 10.1021/acs.nanolett.7b00442. [DOI] [PubMed] [Google Scholar]
  4. Bunch J. S.; Verbridge S. S.; Alden J. S.; van der Zande A. M.; Parpia J. M.; Craighead H. G.; McEuen P. L. Impermeable atomic membranes from graphene sheets. Nano Lett. 2008, 8, 2458–2462. 10.1021/nl801457b. [DOI] [PubMed] [Google Scholar]
  5. Koenig S. P.; Wang L.; Pellegrino J.; Bunch J. S. Selective molecular sieving through porous graphene. Nat. Nanotechnol. 2012, 7, 728–732. 10.1038/nnano.2012.162. [DOI] [PubMed] [Google Scholar]
  6. Smith A. D.; Niklaus F.; Paussa A.; Vaziri S.; Fischer A. C.; Sterner M.; Forsberg F.; Delin A.; Esseni D.; Palestri P.; et al. Electromechanical piezoresistive sensing in suspended graphene membranes. Nano Lett. 2013, 13, 3237–3242. 10.1021/nl401352k. [DOI] [PubMed] [Google Scholar]
  7. Dolleman R. J.; Cartamil-Bueno S. J.; van der Zant H. S. J.; Steeneken P. G. Graphene gas osmometers. 2D Mater. 2017, 4, 011002. 10.1088/2053-1583/4/1/011002. [DOI] [Google Scholar]
  8. Davidovikj D.; Scheepers P. H.; van der Zant H. S. J.; Steeneken P. G. Static capacitive pressure sensing using a single graphene drum. ACS Appl. Mater. Interfaces 2017, 9, 43205–43210. 10.1021/acsami.7b17487. [DOI] [PubMed] [Google Scholar]
  9. Vollebregt S.; Dolleman RJ.; van der Zant H. S. J.; Steeneken PG.; Sarro PM. Suspended graphene beams with tunable gap for squeeze-film pressure sensing. 2017 19th Int. Conf. Solid-State Sens., Actuators Microsyst. 2017, 770–773. 10.1109/TRANSDUCERS.2017.7994162. [DOI] [Google Scholar]
  10. Dolleman R. J.; Davidovikj D.; Cartamil-Bueno S. J.; van der Zant H. S. J.; Steeneken P. G. Graphene squeeze-film pressure sensors. Nano Lett. 2016, 16, 568–571. 10.1021/acs.nanolett.5b04251. [DOI] [PubMed] [Google Scholar]
  11. Verbiest G. J.; Kirchhof J. N.; Sonntag J.; Goldsche M.; Khodkov T.; Stampfer C. Detecting ultrasound vibrations with graphene resonators. Nano Lett. 2018, 18, 5132–5137. 10.1021/acs.nanolett.8b02036. [DOI] [PubMed] [Google Scholar]
  12. Fan X.; Forsberg F.; Smith A. D.; Schroder S.; Wagner S.; Rodjegard H.; Fischer A. C.; Ostling M.; Lemme M. C.; Niklaus F. Graphene ribbons with suspended masses as transducers in ultra-small nanoelectromechanical accelerometers. Nature Electronics 2019, 2, 394–404. 10.1038/s41928-019-0287-1. [DOI] [Google Scholar]
  13. Fan X.; Forsberg F.; Smith A. D.; Schroder S.; Wagner S.; Ostling M.; Lemme M. C.; Niklaus F. Suspended graphene membranes with attached silicon proof masses as piezoresistive nanoelectromechanical systems accelerometers. Nano Lett. 2019, 19, 6788–6799. 10.1021/acs.nanolett.9b01759. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Wittmann S.; Glacer C.; Wagner S.; Pindl S.; Lemme M. C. Graphene membranes for hall sensors and microphones integrated with cmos-compatible processes. ACS Applied Nano Materials 2019, 2, 5079–5085. 10.1021/acsanm.9b00998. [DOI] [Google Scholar]
  15. Blaikie A.; Miller D.; Aleman B. J. A fast and sensitive room-temperature graphene nanomechanical bolometer. Nat. Commun. 2019, 10, 4726. 10.1038/s41467-019-12562-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Dolleman R. J.; Katan A. J.; van der Zant H. S. J.; Steeneken P. G. Semi-permeability of graphene nanodrums in sucrose solution. 2D Mater. 2021, 8, 015031. 10.1088/2053-1583/abbecd. [DOI] [Google Scholar]
  17. Rosłoń I. E.; Dolleman R. J.; Licona H.; Lee M.; Šiškins M.; Lebius H.; Madauß L.; Schleberger M.; Alijani F.; van der Zant H. S. J.; Steeneken P. G. High-frequency gas effusion through nanopores in suspended graphene. Nat. Commun. 2020, 11, 6025. 10.1038/s41467-020-19893-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Siskins M.; Lee M.; Wehenkel D.; van Rijn R.; de Jong T. W.; Renshof J. R.; Hopman B. C.; Peters W. S. J. M.; Davidovikj D.; van der Zant H. S. J.; Steeneken P. G. Sensitive capacitive pressure sensors based on graphene membrane arrays. Microsystems & Nanoengineering 2020, 6, 102. 10.1038/s41378-020-00212-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Lemme M. C.; Wagner S.; Lee K.; Fan X.; Verbiest G. J.; Wittmann S.; Lukas S.; Dolleman R. J.; Niklaus F.; van der Zant H. S. J.; et al. Nanoelectromechanical sensors based on suspended 2D materials. Research 2020, 2020, 8748602. 10.34133/2020/8748602. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Steeneken P. G.; Rijks T. G. S. M.; van Beek J. T. M.; Ulenaers M. J. E.; De Coster J.; Puers R. Dynamics and squeeze film gas damping of a capacitive RF MEMS switch. J. Micromech. Microeng. 2005, 15, 176. 10.1088/0960-1317/15/1/025. [DOI] [Google Scholar]
  21. Bao M.; Yang H. Squeeze film air damping in MEMS. Sens. Actuators, A 2007, 136, 3–27. 10.1016/j.sna.2007.01.008. [DOI] [Google Scholar]
  22. Andrews M.; Harris I.; Turner G. A comparison of squeeze-film theory with measurements on a microstructure. Sens. Actuators, A 1993, 36, 79–87. 10.1016/0924-4247(93)80144-6. [DOI] [Google Scholar]
  23. Andrews M. K.; Turner G. C.; Harris P. D.; Harris I. M. A resonant pressure sensor based on a squeezed film of gas. Sens. Actuators, A 1993, 36, 219–226. 10.1016/0924-4247(93)80196-N. [DOI] [Google Scholar]
  24. Southworth D. R.; Craighead H. G.; Parpia J. M. Pressure dependent resonant frequency of micromechanical drumhead resonators. Appl. Phys. Lett. 2009, 94, 213506. 10.1063/1.3141731. [DOI] [Google Scholar]
  25. Kumar L.; Reimann K.; Goossens M. J.; Besling W. F. A.; Dolleman R. J.; Pijnenburg R. H. W.; van der Avoort C.; Sarro L. P. M.; Steeneken P. G. MEMS oscillating squeeze-film pressure sensor with optoelectronic feedback. J. Micromech. Microeng. 2015, 25, 045011. 10.1088/0960-1317/25/4/045011. [DOI] [Google Scholar]
  26. Naserbakht S.; Dantan A. Squeeze film pressure sensors based on SiN membrane sandwiches. Sens. Actuators, A 2019, 298, 111588. 10.1016/j.sna.2019.111588. [DOI] [Google Scholar]
  27. Dantan A. Membrane sandwich squeeze film pressure sensors. J. Appl. Phys. 2020, 128, 091101. 10.1063/5.0011795. [DOI] [Google Scholar]
  28. Dolleman R. J.; Houri S.; Davidovikj D.; Cartamil-Bueno S. J.; Blanter Y. M.; van der Zant H. S. J.; Steeneken P. G. Optomechanics for thermal characterization of suspended graphene. Phys. Rev. B: Condens. Matter Mater. Phys. 2017, 96, 165421. 10.1103/PhysRevB.96.165421. [DOI] [Google Scholar]
  29. Dolleman R. J.; Davidovikj D.; van der Zant H. S. J.; Steeneken P. G. Amplitude calibration of 2D mechanical resonators by nonlinear optical transduction. Appl. Phys. Lett. 2017, 111, 253104. 10.1063/1.5009909. [DOI] [Google Scholar]
  30. Dolleman R. J.; Houri S.; Chandrashekar A.; Alijani F.; van der Zant H. S. J.; Steeneken P. G. Opto-thermally excited multimode parametric resonance in graphene membranes. Sci. Rep. 2018, 8, 9366. 10.1038/s41598-018-27561-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Dolleman R. J.; Belardinelli P.; Houri S.; van der Zant H. S. J.; Alijani F.; Steeneken P. G. High-frequency stochastic switching of graphene resonators near room temperature. Nano Lett. 2019, 19, 1282–1288. 10.1021/acs.nanolett.8b04862. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Dolleman R. J.; Verbiest G. J.; Blanter Y. M.; van der Zant H. S. J.; Steeneken P. G. Nonequilibrium thermodynamics of acoustic phonons in suspended graphene. Physical Review Research 2020, 2, 012058. 10.1103/PhysRevResearch.2.012058. [DOI] [Google Scholar]
  33. Dolleman R. J.; Hsu M.; Vollebregt S.; Sader J. E.; van der Zant H. S. J.; Steeneken P. G.; Ghatkesar M. K. Mass measurement of graphene using quartz crystal microbalances. Appl. Phys. Lett. 2019, 115, 053102. 10.1063/1.5111086. [DOI] [Google Scholar]
  34. Steeneken P. G.; Dolleman R. J.; Davidovikj D.; Alijani F.; van der Zant H. S. J. Dynamics of 2D material membranes. 2D Mater. 2021, 8, 042001. 10.1088/2053-1583/ac152c. [DOI] [Google Scholar]
  35. Verbridge S. S.; Ilic R.; Craighead H. G.; Parpia J. M. Size and frequency dependent gas damping of nanomechanical resonators. Appl. Phys. Lett. 2008, 93, 013101. 10.1063/1.2952762. [DOI] [Google Scholar]
  36. Blech J. J. On Isothermal Squeeze Films. J. Lubr. Technol. 1983, 105, 615–620. 10.1115/1.3254692. [DOI] [Google Scholar]
  37. Chakraborty D.; van Leeuwen E.; Pelton M.; Sader J. E. Vibration of nanoparticles in viscous fluids. J. Phys. Chem. C 2013, 117, 8536–8544. 10.1021/jp401141b. [DOI] [Google Scholar]
  38. Chakraborty D.; Sader J. E. Constitutive models for linear compressible viscoelastic flows of simple liquids at nanometer length scales. Phys. Fluids 2015, 27, 052002. 10.1063/1.4919620. [DOI] [Google Scholar]
  39. Ladiges D. R.; Sader J. E. Frequency-domain Monte Carlo method for linear oscillatory gas flows. J. Comput. Phys. 2015, 284, 351–366. 10.1016/j.jcp.2014.12.036. [DOI] [Google Scholar]
  40. Ladiges D. R.; Sader J. E. Frequency-domain deviational Monte Carlo method for linear oscillatory gas flows. Phys. Fluids 2015, 27, 102002. 10.1063/1.4932108. [DOI] [Google Scholar]
  41. Suijlen M. A. G.; Koning J. J.; van Gils M. A. J.; Beijerinck H. C. W. Squeeze film damping in the free molecular flow regime with full thermal accommodation. Sens. Actuators, A 2009, 156, 171–179. 10.1016/j.sna.2009.03.025. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nl1c02237_si_001.pdf (1.9MB, pdf)

Articles from Nano Letters are provided here courtesy of American Chemical Society

RESOURCES