Stagnation points control chaotic fluctuations in viscoelastic porous media flow

Significance

Viscoelastic porous media flows become chaotic beyond critical flow conditions, impacting processes including enhanced oil recovery and targeted drug delivery. Understanding how geometric details of the porous medium affect the onset and strength of the chaotic flows can lead to fundamental insights and potential optimization of such processes. Recently, it has been argued that geometric disorder in the medium suppresses chaotic fluctuations. In contrast, we demonstrate that disorder can also significantly enhance fluctuations given a different originally ordered configuration. We show that the occurrence of stagnation points in the flow field is the vital factor controlling the onset and strength of fluctuation, providing a general and intuitive understanding of how pore geometry affects this important class of complex viscoelastic flows.

Abstract

Viscoelastic flows through porous media become unstable and chaotic beyond critical flow conditions, impacting widespread industrial and biological processes such as enhanced oil recovery and drug delivery. Understanding the influence of the pore structure or geometry on the onset of flow instability can lead to fundamental insights into these processes and, potentially, to their optimization. Recently, for viscoelastic flows through porous media modeled by arrays of microscopic posts, Walkama et al. [D. M. Walkama, N. Waisbord, J. S. Guasto, Phys. Rev. Lett. 124, 164501 (2020)] demonstrated that geometric disorder greatly suppressed the strength of the chaotic fluctuations that arose as the flow rate was increased. However, in that work, disorder was only applied to one originally ordered configuration of posts. Here, we demonstrate experimentally that, given a slightly modified ordered array of posts, introducing disorder can also promote chaotic fluctuations. We provide a unifying explanation for these contrasting results by considering the effect of disorder on the occurrence of stagnation points exposed to the flow field, which depends on the nature of the originally ordered post array. This work provides a general understanding of how pore geometry affects the stability of viscoelastic porous media flows.

Unlike viscous Newtonian liquids (e.g., water), many fluids exhibit an elastic response to an applied strain. Such “viscoelastic” fluids are widespread in biology (blood, mucus, synovial fluid) and industry (paints, coatings, fracking fluids). The elasticity is imparted by the presence of a microstructure (formed by, e.g., polymers, proteins, or self-assemblies of lipids or surfactants) that relaxes after deformation (1). The strength of the elastic response of the fluid to an imposed deformation (or flow) is quantified by the Weissenberg number $\text{Wi}=\tau \dot{\gamma }$, with $\tau$ the fluid relaxation time and $\dot{\gamma }$ the rate of strain. While flows of Newtonian fluids become unstable and turbulent due to the onset of inertial effects at high Reynolds number, $\text{Re}\gg 1$, viscoelastic flows can become unstable and exhibit so-called “elastic turbulence” even for $\text{Re}\ll 1$, purely due to elastic effects that arise at high $\text{Wi}$ (2–7).

Viscoelastic porous media flow occurs in diverse processes ranging from enhanced oil recovery (EOR) and filtration to drug delivery (8, 9). Porous media flow subjects a fluid to a complex cycle of deformation with high shear rates through the pore throats or between obstacles and high elongational rates at points of constriction or at stagnation points, leading to stretching of the fluid microstructure if $\text{Wi}\gtrsim 1$ (10, 11). Stagnation points (which occur at the front and rear poles of obstacles in a flow) are particularly effective at causing high stretching and large tensile stresses due to the combination of zero flow velocity and finite velocity gradient that exists in such regions (10–15). Elastic tensile stresses due to stretching on curvilinear streamlines (as through porous media) are conditions well established to lead to linear instabilities in viscoelastic fluids (16–19), which can be precursors to elastic turbulence as $\text{Wi}$ is further increased (7, 20–23). The chaotic fluctuations that result are expected to greatly enhance the pressure loss and the dispersion in porous media, with positive impacts on, for example, removing oil ganglia from the pore space in EOR or improving the distribution of drugs throughout a tumor (24–27).

There have been various recent advances in modeling viscoelastic porous media flows both experimentally and numerically (14, 27–36). However, the complexity of the problem has limited numerical simulations to extremely simplified regular geometries (32, 36) and/or small computational domains and/or regimes of low $\text{Wi}$ (31). Experimentally, Browne and coworkers (27, 33) have achieved the detailed characterization of the pore-scale dynamics in model porous media formed by three-dimensional (3D) random packings of spherical glass particles, correlating a global increase in the pressure drop across the media with the onset of elastic turbulence in the pores. Importantly, due to the complexity of the random sphere packings of Browne and coworkers (27, 33), fluid arriving at each pore experiences a unique flow history, and the flow through different pores becomes unstable at different values of the nominal $\text{Wi}$ (computed based on macroscopic flow conditions). Fundamental questions remain over how the details of the pore-space geometry affect the onset and strength of the chaotic fluctuations that arise.

While randomly packed beds of polydisperse spheres provide a good model for the complex pore geometries that arise in real media such as sandstone or carbonate rock (37, 38), ordered and regular geometries enable investigation of the role of different packing structures and hence, pore shape (29, 39, 40). This is most conveniently achieved by arrangements of posts forming either linear models of the interconnecting capillary network through the pore space (e.g., refs. 36, 41, and 42) or two-dimensional (2D) arrays that represent the tortuous flow paths around closely spaced grains (e.g., refs. 14, 24, 25, 28, 30, 35, 43, and 44).

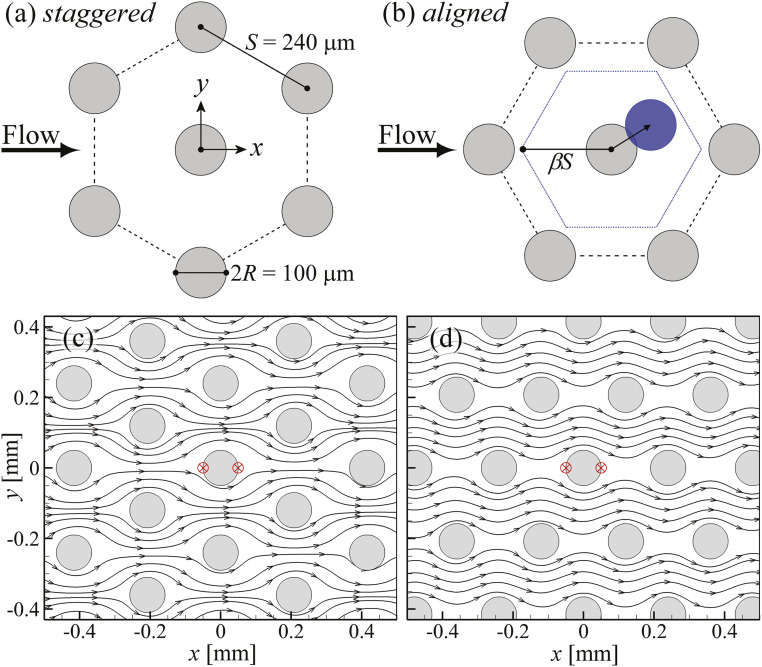
An outstanding open question concerns how the chaotic dynamics of viscoelastic flows are affected when geometric disorder (inherent in real heterogeneous systems) is introduced to a regular model porous medium. In a recent attempt to address this issue, Walkama et al. (28) performed experiments in a series of 2D microfluidic post arrays using shear thinning viscoelastic polymeric test solutions. They examined how the introduction of increasing random disorder to a hexagonal post array (arranged as shown in Fig. 1A) affected the onset and strength of the chaotic fluctuations observed for $\text{Wi}\gtrsim 1$. Their results led to the broad general conclusion that “disorder suppresses chaos in viscoelastic flows.” However, other works have shown that instabilities and fluctuations in viscoelastic flows through 2D ordered post arrays strongly depend on the orientation of the array relative to the flow direction (30). Thus, different behavior might be anticipated from an ordered array of posts that are staggered along the flow direction (Fig. 1A) (as employed in ref. 28) than from an identical array rotated by $\mathrm{30}°$ such that the posts become aligned (Fig. 1B). Indeed, as shown in Fig. 1 C and D, even the low-$\text{Re}$ flow of a simple Newtonian fluid shows qualitatively different flow patterns in the two contrasting post arrangements. Notably, in Fig. 1C, it is clear that each post presents both an upstream point and a downstream stagnation point that are accessible to the flow field. However, in the rotated arrangement in Fig. 1D, the flow is concentrated between the aligned rows of posts, largely bypassing the stagnation points. Given the known role of stagnation point regions in driving the onset of instabilities and fluctuations in viscoelastic flows (e.g., refs. 15, 17, and 45–49), we question the generality of the conclusions drawn by Walkama et al. (28), based on modifications made to a single-ordered geometry like in Fig. 1 A and C.

Fig. 1.

(A and B) Unit cell representations of two contrasting ordered hexagonal arrays of posts used in the flow experiments. In A, the posts are staggered along the $x$ direction in which the flow is imposed. The post radius is $R$, and lattice spacing is $S$. Rotating the array by $\mathrm{30}°$ aligns the posts in the flow direction (B). Disordered aligned arrays are generated by the random displacement of each post within a hexagon of circumradius $\beta S$, as described in ref. 28. (C and D) Streamlines determined by flow velocimetry (Materials and Methods) with a Newtonian fluid in the staggered (C) and aligned (D) arrays at $\text{Re}\approx 10^{-3}$. The red crossed circles in C and D indicate the locations of the leading and trailing-edge stagnation points on one of the circular posts.

Here, we show by microfluidic experiments with a viscoelastic wormlike micelle (WLM) solution that a rotation of the hexagonal post array in Fig. 1 A and C in order to align the posts with the flow direction (Fig. 1 B and D) strongly suppresses the chaotic fluctuations for a range of $\text{Wi}\gtrsim 1$, consistent with our expectation based on the removal of stagnation points. Subsequently, following the methods of Walkama et al. (28), we introduce random disorder to the aligned array of posts (Fig. 1B). In this case, contrary to Walkama et al. (28), disorder does not further suppress but rather, promotes chaotic fluctuations over a wide range of $\text{Wi}$. Although our results appear to contradict those recently reported in Walkama et al. (28), both are simply explained by considering how disorder affects the prominence of stagnation points in the flow field (which is opposite, depending on the originally ordered geometric arrangement). Furthermore, we significantly extend the range of imposed $\text{Wi}$ beyond that studied by Walkama et al. (28), showing that at sufficiently high $\text{Wi}$, the nature of the flow fluctuations becomes essentially geometry independent. Our work reaches an intuitive and general understanding of the role of geometry (specifically the importance of stagnation points) in controlling the onset and strength of chaotic fluctuations in viscoelastic porous media flows.

Results

Experiments are conducted in microfluidic channels ($W=2.4$-mm wide, $H=1$-mm high, and 25-mm long) containing arrays of $\approx 300$ circular posts (radius $R=50\hspace{0.17em}\mathrm{\mu }$m). Two of the channels contain ordered hexagonal arrays (disorder $\beta =0$, lattice spacing $S=240\hspace{0.17em}\mathrm{\mu }$m) in either “staggered” or “aligned” orientations (Fig. 1 A and B, respectively). Five additional aligned arrays have increasing degrees of random disordering with $\beta =\left[0.05,0.1,0.2,0.3,0.4\right]$, where the disorder is introduced by the same method reported in ref. 28, as illustrated schematically in Fig. 1B. All seven arrays have the same porosity $\varphi \approx 0.84$.

The model viscoelastic test fluid is an aqueous WLM solution composed of 100 mM cetylpyridinium chloride (CPyCl) and 60 mM sodium salicylate (NaSal) (50). The fluid is shear thinning with a zero shear viscosity ${\eta }_0\approx 48$ Pa$\cdot$s and a single-mode Maxwell relaxation time $\tau =1.5$ s (Fig. 2). Flow through the post arrays is driven by a syringe pump (neMESYS; Cetoni GmbH) infusing at controlled volumetric flow rate $Q$; hence, average flow velocity $U=Q/\varphi WH$, and characteristic deformation rate $\dot{\gamma }=U/R$. The maximum Reynolds number, $\text{Re}=\rho UR/\eta \left(\dot{\gamma }\right)<10^{-5}$ (where $\rho$ is the density and $\eta \left(\dot{\gamma }\right)$ is the shear rate–dependent viscosity), means that inertia can be neglected.

Fig. 2.

Rheometric characterization of the 100:60 mM CPyCl:NaSal WLM test solution in (A) steady shear and (B) small-amplitude oscillation at $\mathrm{25}°$C in a DHR3 rotational rheometer (TA instruments Inc.) fitted with a 40-mm-diameter $\mathrm{1}°$ cone and plate geometry. The steady shear flow curve in A is described by the C-Y model, and the storage and loss moduli in B are described by a single-mode Maxwell model (Materials and Methods).

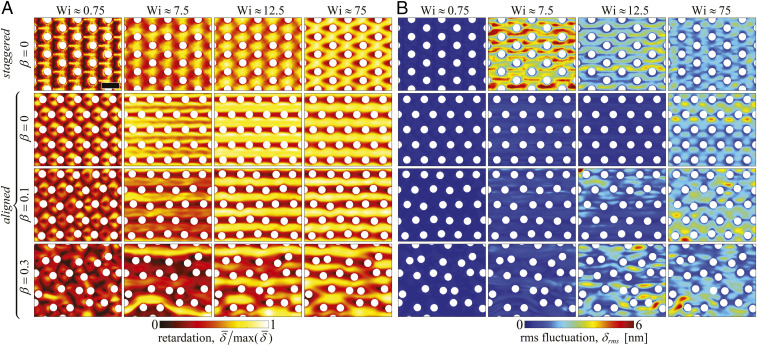
A high-speed polarizing camera (CRYSTA PI-1P; Photron Ltd.) is used to visualize the regions of high micelle orientation and elastic stress in the post arrays over a range of imposed $\text{Wi}=\tau \dot{\gamma }$, via the flow-induced optical retardation, $\delta$. Time-averaged fields $\overline{\delta }={⟨\delta ⟩}_t$, captured at 125 Hz, are shown for a few of the arrays and several values of $\text{Wi}$, alongside the corresponding local rms fluctuations ${\delta }_{rms}=\sqrt{{⟨{\left(\delta -\overline{\delta }\right)}^2⟩}_t}$ (Fig. 3). For the ordered staggered geometry ($\beta =0$) (first row of Fig. 3), at low $\text{Wi}\approx 0.75$ each post has an associated downstream wake of high retardation, of similar appearance to that seen downstream of isolated cylinders (15). This indicates that the downstream stagnation point of each post is effective at orienting and stretching the micellar microstructure. At $\text{Wi}\approx 0.75$, the flow is steady, and the rms fluctuations are low. For increasing $\text{Wi}$, the flow becomes time dependent, and at $\text{Wi}\approx 7.5$, strong fluctuations are observed. The fluctuation appears as the transverse wagging motion of each downstream wake (Movie S1). The growth of fluctuations with $\text{Wi}$ is consistent with the recent experiments reported in ref. 28 using a similar staggered hexagonal array and over a similar range of $\text{Wi}\lesssim 7.5$. We have significantly extended the range of $\text{Wi}$ beyond this value, and we observe that fluctuations remain but apparently become less intense for $\text{Wi}\gtrsim 7.5$. For $\text{Wi}\approx 75$ (and beyond), the fluctuations appear more uniformly throughout the field and are of increased frequency compared with $\text{Wi}\approx 7.5$ (Movie S2).

Fig. 3.

Evolution of the retardation fields with increasing $\text{Wi}$ for the WLM solution in the ordered staggered post array and in aligned arrays with various disorder $\beta$: (A) normalized, time-averaged retardation fields $\overline{\delta }/max\left(\overline{\delta }\right)$ and (B) local retardation fluctuations ${\delta }_{rms}$. Flow is from left to right (i.e., along the $x$ direction), and the field of view is centered at the coordinate origin at the center of each array (54% of full field of view shown). (Scale bar: $250\hspace{0.17em}\mathrm{\mu }$m.)

In the ordered aligned geometry ($\beta =0$) (second row of Fig. 3), the retardation field at $\text{Wi}\approx 0.75$ is qualitatively different from the staggered array. Here, there is no significant downstream wake, and the regions of high stress are concentrated upstream and to the sides of each post. As $\text{Wi}$ is increased, the retardation becomes concentrated in the gaps between the rows of aligned posts. Fluctuations in the ordered aligned array remain low relative to the staggered array until, for $\text{Wi}\approx 75$, a similar level of time dependence is observed throughout the field. Movies S3 and S4 show the time-resolved retardation at $\text{Wi}\approx 7.5$ and $\text{Wi}\approx 75$, respectively.

For increasing disorder of the aligned array ($\beta =0.1$ and $\beta =0.3$) (third and fourth rows of Fig. 3, respectively), at low $\text{Wi}\approx 0.75$, high stress wakes appear downstream of a few of the posts, although unlike in the staggered array, these are not necessarily aligned in the primary flow ($x$) direction owing to the disorder. At intermediate $\text{Wi}\approx 7.5$ and $\text{Wi}\approx 12.5$, the flow becomes unsteady, and although less intense than for the staggered array, fluctuations are clearly greater than for the aligned array with $\beta =0$. For the highest $\text{Wi}$ shown ($\text{Wi}\approx 75$), fluctuations are roughly similar in all arrays.

Spatially averaged rms retardation fluctuations ${⟨{\delta }_{rms}⟩}_i$ in the staggered array show a large local peak at intermediate $\text{Wi}\approx 7.5$, followed by a reduction and a subsequent growth toward an apparent high-$\text{Wi}$ plateau (Fig. 4). In the aligned geometry ($\beta =0$), the peak at intermediate $\text{Wi}$ is greatly diminished, although at higher $\text{Wi}$, fluctuations reach a similar plateau value as for the staggered array. With increasing disorder of the aligned geometry, the fluctuations at intermediate $\text{Wi}$ increase. At $\beta =0.4$, a peak emerges at a similar $\text{Wi}$ as the peak seen in the staggered array. At higher $\text{Wi}$, most of the geometries tend to a similar limiting plateau in the level of fluctuation; however, at $\beta =0.1$, fluctuations remain higher than those for $\beta =0$.

Fig. 4.

Spatially averaged retardation fluctuations ${⟨{\delta }_{rms}⟩}_i$ vs. $\text{Wi}$ in various post arrays. The shaded gray region about the data for the aligned array with $\beta =0$ indicates the typical variability over repeated test runs. Inset compares fluctuations between the ordered and disordered aligned arrays. For the aligned array, disorder tends to increase temporal fluctuations over a wide range of $\text{Wi}$.

Spatially averaged fluctuations from the disordered arrays are compared against those from the ordered aligned array as $\left({⟨{\delta }_{rms}⟩}_i-{⟨{\delta }_{rms,\beta =0}⟩}_i\right)/{⟨{\delta }_{rms,\beta =0}⟩}_i$ (Fig. 4, Inset). Within experimental error, the data for $\beta =0.05$ do not deviate significantly from zero, but for $\beta >0.05$, all of the disordered arrays show a relative peak in the fluctuations around $\text{Wi}\approx 10$ where ${⟨{\delta }_{rms}⟩}_i\approx 2\times {⟨{\delta }_{rms,\beta =0}⟩}_i$. Perhaps surprisingly, the increase in fluctuations is saturated (or maximal) for a rather low disorder of $\beta =0.1$. It is noted that Walkama et al. (28) showed that small amounts of disorder were also sufficient to strongly suppress the fluctuations occurring in a staggered post array configuration.

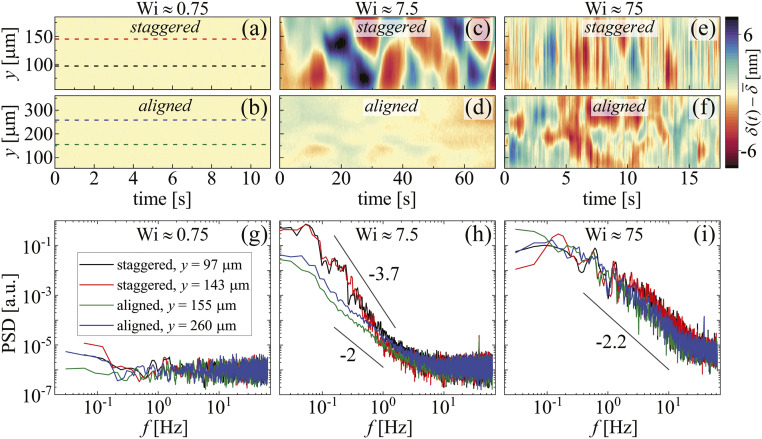
Analysis of retardation fluctuations about the local mean $\delta \left(t\right)-\overline{\delta }$ in the ordered staggered and aligned arrays ($\beta =0$) at three representative values of $\text{Wi}$ is provided in Fig. 5. Kymographs of the fluctuations (Fig. 5 A–F) are extracted along the line $x=0$ between the post located at the origin and its neighbor located to positive $y$. For low $\text{Wi}\approx 0.75$, the fluctuations in both the staggered (Fig. 5A) and ordered aligned (Fig. 5B) arrays are weak, and the kymographs indicate the noise level of the measurement. At this $\text{Wi}$, the power spectral density (PSD) of the fluctuations with time along the four colored dashed lines all show a uniformly flat frequency response (Fig. 5G). At intermediate $\text{Wi}\approx 7.5$, the strong fluctuations in the staggered array (Fig. 5C) translate to a PSD with high power at low frequencies that decays steeply into the noise with a power law exponent $-3.7$ (Fig. 5H). In contrast, in the ordered aligned array at $\text{Wi}\approx 7.5$ (Fig. 5 D and H), the fluctuations are an order of magnitude weaker at low frequencies and decay with an exponent $-2$. At high $\text{Wi}\approx 75$, both the staggered and the ordered aligned arrays show fluctuations of similar intensity (Fig. 5 E and F) and with similar frequency content in the PSD (Fig. 5I). The PSD is shifted to higher frequencies than at $\text{Wi}\approx 7.5$ and decays with an exponent of $\approx -2.2$. The power law decays in the power spectra of the fluctuating signals indicate that the fluctuations are aperiodic, and the slopes are consistent with values reported in studies of elastic turbulence (7, 21, 26–28).

Fig. 5.

Analysis of retardation fluctuations about the local mean $\delta \left(t\right)-\overline{\delta }$ in the ordered staggered and aligned arrays ($\beta =0$). Kymographs of the fluctuations along $x=0$ for (A and B) $\text{Wi}\approx 0.75$, (C and D) $\text{Wi}\approx 7.5$, and (E and F) $\text{Wi}\approx 75$. PSD distributions of the fluctuations for (G) $\text{Wi}\approx 0.75$, (H) $\text{Wi}\approx 7.5$, and (I) $\text{Wi}\approx 75$, taken along the correspondingly colored horizontal dashed lines in A and B.

Our results reveal a broad consistency with those of Walkama et al. (28) for viscoelastic flow through an ordered staggered array of posts. However, introducing disorder to an aligned array has a diametrically opposite effect from that shown by Walkama et al. (28) for introducing disorder to a staggered array. Disordering an aligned array causes chaotic flow fluctuations to be enhanced rather than suppressed. These contrasting results can be understood in context with each other by using microparticle image velocimetry ($\mathrm{\mu }$-PIV) to measure the flow fields through the arrays at low $\text{Wi}$ prior to the onset of instability. From the measured velocity fields $\mathbf{u}=\left(u,v\right)$, the deformation rate $\mathbf{D}$ and vorticity $\mathbf{\Omega }$ tensors are computed. Fig. 6, Left shows the normalized magnitude of the velocity fields $\left|\mathbf{u}\right|/max\left(\left|\mathbf{u}\right|\right)$. To indicate the local flow kinematics, Fig. 6, Center shows the “flow-type parameter” $\xi =\left(\left|\mathbf{D}\right|-\left|\mathbf{\Omega }\right|\right)/\left(\left|\mathbf{D}\right|+\left|\mathbf{\Omega }\right|\right)$, where $\left|\mathbf{D}\right|=\sqrt{2\mathbf{D}:\mathbf{D}}$ and $\left|\mathbf{\Omega }\right|=\sqrt{2\mathbf{\Omega }:\mathbf{\Omega }}$ (51). Here, $\xi =-1$ indicates solid body rotation, $\xi =0$ indicates simple shear, and $\xi =1$ indicates pure extension. The flow strength in the extensional regions is quantified by the principle strain rate [or eigenvector of $\mathbf{D}$ (52)], ${\lambda }_1=\frac{1}{2}\sqrt{{\left({\mathbf{D}}_{11}-{\mathbf{D}}_{22}\right)}^2+4{\mathbf{D}}_{12}^2}$ (Fig. 6, Right). In the staggered array (Fig. 6, row 1), it is evident that streamlines diverge upstream of each post and reconverge downstream, resulting in extension-dominated regions at the up- and downstream stagnation points. Extensional rates are particularly high downstream of each post, where elastic stresses are also high (Fig. 3) and time dependence is first manifested (Movie S1). By contrast, in the ordered aligned array (Fig. 6, row 2), the flow is concentrated in between the aligned rows of posts, and streamlines do not connect between successive streamwise-oriented posts. Every stagnation point is thus effectively “screened” from the flow field. It is notable that, for the ordered aligned array, the flow-type parameter shows regions of extensional flow between the aligned posts. However, this is inevitable due to the symmetry of the flow about $y=0$ and highlights that the flow-type parameter alone does not provide a complete picture; it is necessary to also consider deformation rates in the regions of interest (53). In the case of the ordered aligned array, the principal strain rate ${\lambda }_1$ in the extension-dominated regions is weak, indicating that micelle deformation in these regions will also be weak (consistent with the corresponding retardation image shown in Fig. 3). We remark that the velocity fields measured in the ordered hexagonal staggered and aligned arrays in Fig. 6 are also consistent with the qualitative flow visualization shown by Kawale et al. (30) made for polymer solutions flowing in similar arrangements of posts. As disorder is applied to the aligned array (Fig. 6, rows 3 and 4), locations emerge where streamlines split and reconverge, reintroducing stagnation points to the flow field. It becomes possible to identify posts downstream of which both the flow kinematics are extension dominated, and the streamwise-oriented strain rates are high (examples are marked by gray arrowheads in Fig. 6).

Fig. 6.

Flow velocimetry in various post arrays at $\text{Wi}\approx 0.75$: (Left) Normalized flow speed $\left|\mathbf{u}\right|/max\left(\left|\mathbf{u}\right|\right)$. (Center) Flow-type parameter $\xi$. (Right) Normalized principal strain rate ${\lambda }_1/\left(U/R\right)$. Disordering the aligned array introduces stagnation points, where extension-dominated regions also have high strain rates (examples are indicated by gray arrowheads). (Scale bar: $250\hspace{0.17em}\mathrm{\mu }$m.)

Discussion

Contrary to the conclusions of Walkama et al. (28), our results clearly show that disorder does not necessarily suppress chaotic fluctuations in viscoelastic flows. Depending on the original ordered configuration, disorder can, in fact, promote such fluctuations over a range of $\text{Wi}$. In general, this can be understood by considering the rate of occurrence of stagnation points in the flow field. Stagnation points are locations prone to elastic instability due to the high tensile stresses they induce and the consequent feedback on the locally curving streamlines (13, 15, 17, 23, 45–48, 54). In particular, for viscoelastic flows around posts, it is quite well established that instability onset scales with geometric parameters and the imposed $\text{Wi}$ according to the well-known criterion proposed by McKinley and coworkers (16, 17). This scaling is based on the curvature of streamlines and the elastic tensile stress close to the rear stagnation point of the post, indicating that this location is the most sensitive to stability loss. Several recent papers examining flows of viscoelastic polymer and wormlike micellar solutions around isolated cylinders confined in microfluidic channels clearly confirm that instabilities originate at the rear stagnation point (15, 49, 57–60).

In the ordered staggered configuration considered both here and in ref. 28, the number of stagnation points is maximized; every array element contributes both an upstream and a downstream stagnation point. Thus, disordering a staggered array (as performed in ref. 28) can only serve to reduce the incidence of such locations; effectively, disorder will result in some posts becoming hidden in the wakes of others, thus screening their stagnation points and suppressing fluctuations. By contrast, in the ordered aligned array considered here, every stagnation point is screened from the flow field by the previous upstream post (i.e., stagnation points are minimized). In this case, introducing disorder must inevitably expose new stagnation points to the flow field, introducing locations where instability and strong fluctuations will initiate as $\text{Wi}$ is increased. An equivalent, but perhaps more intuitive, way to express this is as follows; disordering a staggered array tends to open free paths for the fluid to flow (as shown in ref. 28), but disordering an aligned array acts to block the free paths that previously existed. Naturally, for high disorders, both staggered and aligned configurations should tend toward randomness, hence homogeneity. Note that the stagnation point screening effect between streamwise-oriented posts is also evident in recent viscoelastic numerical simulations presented by Kumar and Ardekani (61).

By examining the effect of disorder on a contrasting geometry from that presented by Walkama et al. (28) and considering the results of both studies as a whole, we are able to arrive at a far more general understanding of how the onset of instability and chaos in viscoelastic flows through porous media depends on the features of the flow geometry. We note that, at present, our arguments regarding the importance of stagnation points are based on a logical and intuitive understanding that emerges from the combination of our results and those of ref. 28. Future work will employ experimental and/or numerical approaches to attempt a more direct correlation between the flow fluctuations and the occurrence of stagnation points per unit area of array.

It should be mentioned that we have maintained the ratio of post radius $R$ to lattice spacing $S$ the same as employed in ref. 28 in order to provide a counterexample to the prior work while retaining equivalent porosity. However, it is certain that other geometric factors such as the array porosity (e.g., ref. 24) and the post shape (e.g., ref. 30) will also have a strong influence on the flow behavior. As an obvious example, if the porosity of the aligned array was sufficiently reduced, the flow could be expected to redevelop in the space between the aligned posts, thus exposing their stagnation points. In contrast, reducing the porosity of the staggered array might be expected to enhance the velocity gradients near the stagnation points. As alluded to above, we expect the general principles of the elastic instability criterion of McKinley and coworkers (16, 17) to hold in viscoelastic porous media flows. Manipulating the porosity of ordered post arrays in order to vary the streamline curvature would be one way to confirm if the predicted scaling is indeed universal. Attempting to further extrapolate our results to understand fluctuations that arise in random 3D packed beds more representative of real porous media (c.f., refs. 27 and 33), it is possible that the presence (or absence) of a stagnation point immediately upstream of a pore influences the $\text{Wi}$ at which flow in the pore becomes unstable, thus explaining the pore-scale heterogeneity of the fluctuations observed. It would be of great interest to apply the pore-level visualization methods of Browne and coworkers (27, 33) to examine viscoelastic flows in ordered 3D porous media in which stagnation points could be introduced (or removed) locally. This should be possible by the 3D printing technique of selective laser-induced etching (SLE) (62, 63) and is a focus of current research efforts.

It is also worthwhile mentioning that in this work, we have employed higher–aspect ratio microfluidic devices than those used by Walkama et al. (28) ($H/W\approx 0.42$ here, but $H/W\approx 0.013$ in ref. 28), where the large channel height $H$ in the present case was primarily to enable the acquisition of the retardation signals (Fig. 3). We also employed a viscoelastic WLM solution in favor of a polymer solution since WLM solutions show a greater degree of optical anisotropy under flow. However, our flow velocimetry in the ordered post arrays (Fig. 6) is quite consistent with the qualitative flow visualization provided by Kawale et al. (30), who used similar polymeric fluids as those employed in ref. 28 and similarly low–aspect ratio microfluidic devices ($H/W\approx 0.048$). Our results also compare favorably with recently reported 2D numerical simulations employing a viscoelastic constitutive model appropriate for shear thinning polymer solutions (64). Furthermore, in previous experiments on flows around isolated posts, we found a close correspondence between the behavior of polymeric and WLM fluids (15, 57, 60). In those prior works, the onset and nature of instability depended on the strength of shear thinning as well as of elastic forces in the flow (49, 57). We expect the same to be true in post arrays, so a full parametric study of rheological effects would be valuable. This would provide another potential route to confirming the scaling of the elastic instability criterion of McKinley et al. (16, 17).

Finally, we reiterate that, in the present work, fluctuations become effectively geometry independent at sufficiently high $\text{Wi}$, where both staggered and aligned configurations show very similar characteristics in their power spectra, indicative of elastic turbulence. This should not be surprising since any viscoelastic flow with streamline curvature will become linearly unstable beyond a certain critical $\text{Wi}$ (6, 16, 17, 19); however, it was not observed by Walkama et al. (28) as their experiments were restricted to much lower $\text{Wi}$ than accessed here ($\text{Wi}\lesssim 10$ in ref. 28, but $\text{Wi}>100$ here).

This work serves as a demonstration of the crucial importance of geometry in determining the onset and strength of chaotic fluctuations in viscoelastic flows. In particular, over a range of $\text{Wi}$, a disorder of just $\beta =0.1$ applied to an aligned array of posts can increase rms fluctuations by up to $\approx 100\%$, suggesting that even relatively few stagnation points in a flow field can have a significant impact on the global dynamics of viscoelastic flows.

Materials and Methods

Microfluidic Device Fabrication.

Microfluidic post array devices were fabricated in fused silica glass by the technique of SLE (65), implemented on a commercial LightFab SLE system [LightFab GmbH (62, 63)].

Viscoelastic Test Fluid Characterization.

The aqueous 100:60 mM CPyCl:NaSal WLM solution was characterized rheometrically at $\mathrm{25}°$C on a DHR3 rotational rheometer (TA Instruments Inc.) equipped with a 40-mm-diameter, $\mathrm{1}°$ cone and plate fixture (Fig. 2). In steady shear (Fig. 2A), the viscosity function is well described by the Carreau–Yasuda generalized Newtonian fluid (C-Y) model:

$$\eta ={\eta }_{\infty }+\frac{{\eta }_0-{\eta }_{\infty }}{{\left[1+{\left(\dot{\gamma }/\dot{\gamma }*\right)}^a\right]}^{\left(1-n\right)/a}},$$ [1]

where ${\eta }_{\infty }=0.001$ Pa$\cdot$s is the infinite–shear rate viscosity, ${\eta }_0=48$ Pa$\cdot$s is the zero–shear rate viscosity, $\dot{\gamma }*=0.45$ ${\mathrm{s}}^{-1}$ is the characteristic shear rate for the onset of shear thinning, $n=0$ is the “power law exponent” in the shear thinning region, and $a=2$ is a dimensionless fitting parameter that controls the rate of the transition between the constant viscosity and the shear thinning regions. The C-Y model fit to the viscosity function is used to compute characteristic values of $\eta \left(\dot{\gamma }\right)$ inside the post arrays for the estimation of the Reynolds number.

The storage and loss moduli, $G^{\prime }$ and $G^{″}$, of the WLM test solution (Fig. 2B) were determined by small-angle oscillatory shear measurements made at 5% strain over a range of angular frequency $0.01\le \omega \le 100$ rad ${\mathrm{s}}^{-1}$. The data are well described over most of the frequency range using a single-mode Maxwell model:

$$G^{\prime }\left(\omega \right)=\frac{G_0{\left(\tau \omega \right)}^2}{1+{\left(\tau \omega \right)}^2};G^{″}\left(\omega \right)=\frac{G_0\tau \omega }{1+{\left(\tau \omega \right)}^2},$$ [2]

providing values for the Maxwell relaxation time $\tau =1.5$ s and plateau modulus $G_0=30.2$ Pa.

Flow-Induced Retardation Measurement.

Spatially resolved optical retardation due to microstructural orientation in the flowing WLM test solution is measured using a high-speed polarization camera [CRYSTA PI-1P; Photron Ltd. (59)] that combines a “micropolarizer array” with a complementary metal–oxide–semiconductor (CMOS) imaging sensor. The micropolarizer array consists of $\mathrm{1,024}\times \mathrm{1,024}$ linear polarizing elements, each the size of one pixel of the $\mathrm{1,024}\times \mathrm{1,024}$ CMOS sensor. The polarizing elements are arranged in sets of $2\times 2$ with orientations of $0°$, $45°$, $90°$, and $135°$. White light is passed through a band-pass filter (520 nm) and a circular polarizer before passing through the sample and being focused by a $10\times$ objective lens through the micropolarizer array and onto the imaging sensor. Analysis of the light intensity received at the individual pixels in each set of four provides a spatially resolved and quantitative measurement of the retardation, $\delta$, and the orientation angle, $\theta$. The retardation describes the total phase shift occurring as light polarized at $\theta$ and $\theta +90°$ passes through the sample, which is due to the difference in the refractive indices ($n_1$ and $n_2$) along the two orthogonal directions (i.e., the birefringence $\mathrm{\Delta }n=n_1-n_2$). The birefringence is related to the retardation by $\mathrm{\Delta }n=\delta /\ell$, where $\ell$ is the path length through the birefringent material (66, 67). Images are captured at 125 Hz and have a spatial resolution of $\approx 1.8\hspace{0.17em}\mathrm{\mu }$m.

Flow Velocimetry.

Flow velocimetry was performed using a FlowMaster volume illumination $\mathrm{\mu }$-PIV system [LaVision GmbH (68, 69)]. The $xy$ plane at the midheight ($H/2$) of the post arrays was imaged at $12\times$ magnification on a microscope (SteREO Discovery V20; Zeiss), while a dual-pulsed neodymium-doped yttrium lithium fluoride (Nd:YLF) laser synchronized with a high-speed camera (Phantom VEO410; Vision Research Inc.) operating in frame-straddling mode excited the fluorescence of 2-μm-diameter tracers (PS-FluoRed; Microparticles GmbH) seeded in the test fluid. One hundred image pairs captured at 12 Hz were processed by a standard particle image velocimetry algorithm implemented in DaVis software (LaVision GmbH) and averaged to obtain velocity vectors $\mathbf{u}=\left(u,v\right)$ spaced at $\approx 13\hspace{0.17em}\mathrm{\mu }$m in $x$ and $y$. For this setup, the measurement depth over which particles contribute to the determination of velocity vectors is $\approx 230\hspace{0.17em}\mathrm{\mu }$m (70).

Data Availability

All study data are included in the article and/or supporting information.