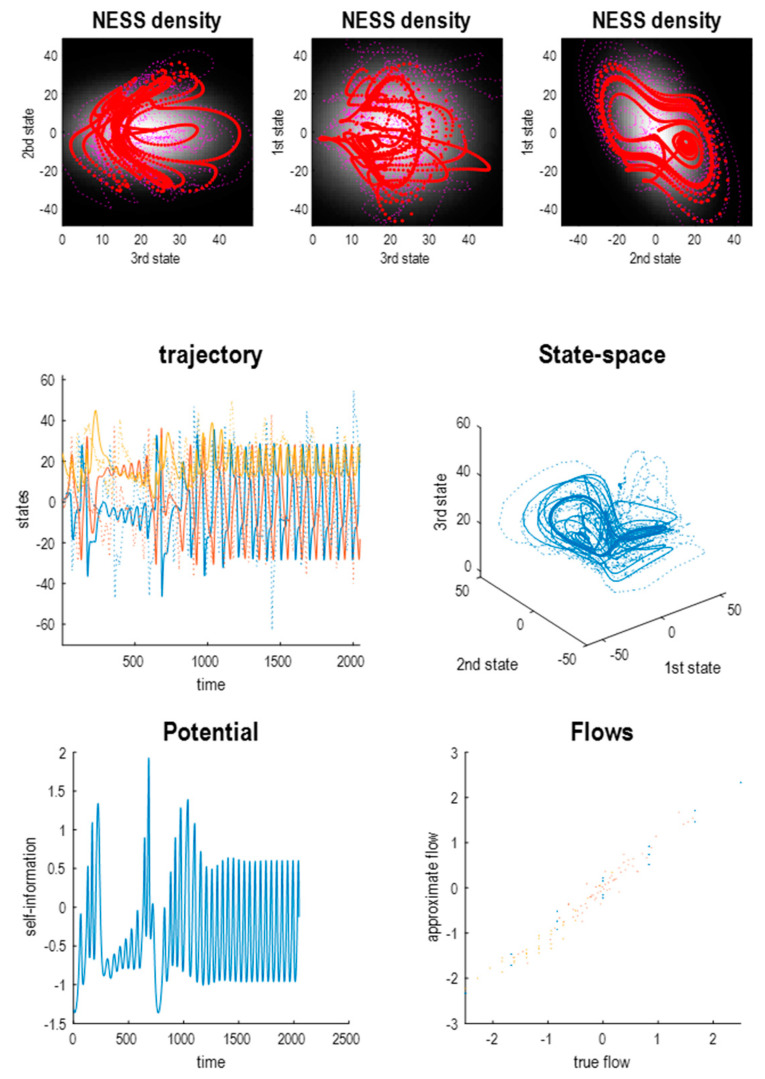
Figure 3.

A chaotic Laplacian system. (Upper panels) these show the solution or trajectory of three states comprising a Laplacian approximation to a stochastic Lorenz system. The red dots mark a deterministic solution to the equations of motion, while the purple dots illustrate a stochastic solution with random fluctuations. These trajectories are superimposed on an image representation of the nonequilibrium steady-state density that—by construction in this Laplacian system—is multivariate Gaussian. (Middle panels) the left panel shows the deterministic (solid lines) and stochastic (dotted lines) solutions as a function of time, while the right panel plots the same trajectories in state-space. The shape of the attractor retains a butterfly-like form but is clearly different from the Lorenz attractor. (Lower left panel) this plots the potential or self-information as a function of time based upon the analytic form for the equations of motion and the deterministic trajectory of the previous panel. In the absence of the correction term, the gradient flow would ensure that this potential decreased over time, because solenoidal flow is divergence free (i.e., is conservative). However, there are slight fluctuations around the minimum potential induced by the correction term. (Lower right panel) this plots the flow of the Laplacian system (approximate flow) against the flow of the Lorenz system (true flow) evaluated at 64 equally spaced sample points. The different colours correspond to the components of flow or motion in the three dimensions. It can be seen that although there is a high correlation between the flows of the Laplacian and Lorenz systems, they are not identical.