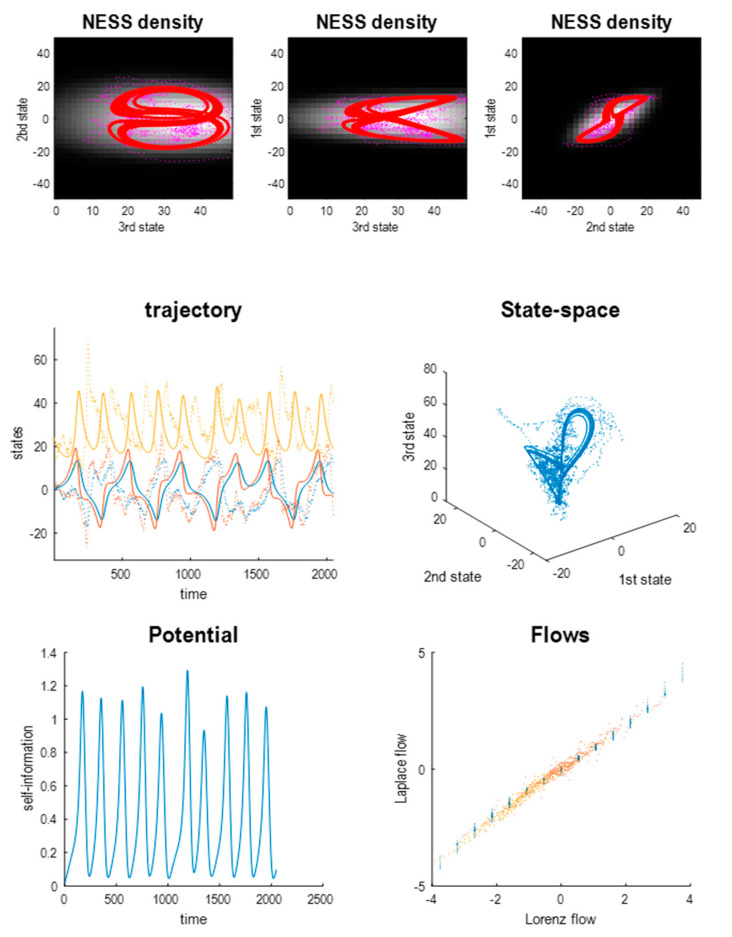
Figure 5.

A high-order approximation. This figure uses the same format as Figure 3 to illustrate the dynamics of a three-dimensional system that is indistinguishable from a Lorentz system. However, in this instance, the equations of motion can be decomposed into a solenoidal and gradient flow in which the dissipative part of the flow operator and Hessian are positive definite. In other words, this system is apt to describe stochastic chaos driven by random fluctuations to a proper nonequilibrium steady-state density. In this example, the solenoidal flow was parameterised up to second-order and the potential up to fourth-order, with constraints to ensure the Hessian was positive definite everywhere. The high order terms in the Hessian mean that the steady-state density in the upper panels is no longer Gaussian (although univariate and bivariate conditional densities remain Gaussian).