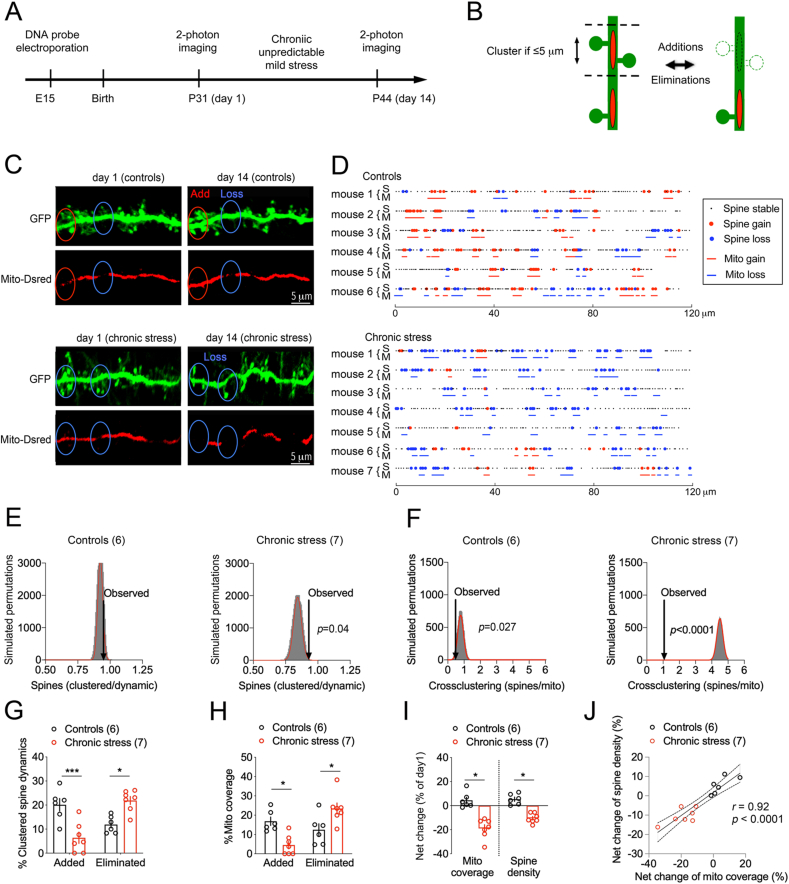
Fig. 4.

Mitochondrial network remodeling at sites of dendritic spine turnover.

A. Experimental timeline.

B. Working model.

C. Two-photon images of dendritic Mito-dsRed and GFP in pyramidal neurons of cortex before and after chronic stress. A distance ≤5 μm is indicated where the loss/gain of groups of spines corresponded with the loss/gain of mitochondrial coverage.

D. Topography of mitochondria (M) and spine (S) remodeling in dendritic territories imaged twice 14 days apart.

E. Clustered spine dynamics is greater than chance. Histogram shows the distribution of spine permutations in 30,000 simulations of randomized new spine positions (mean Gaussian fit = 0.94 ± 0.014, observed = 0.97 ± 0.35, N = 6 Controls, p = 0.1 and mean Gaussian fit = 0.84 ± 0.03, observed = 0.93 ± 0.1, N = 7 Stress, p = 0.04).

F. Cross-clustering of proximal (≤5 μm) spine dynamics and mito remodeling is greater than chance. Histogram shows the distribution of spine permutations in 30,000 simulations of randomized new spine positions with respect to mito remodeling (mean Gaussian fit = 0.786 ± 0.17, observed = 0.58 ± 0.075, N = 6 Controls, p = 0.027 and mean Gaussian fit = 4.5 ± 0.18, observed = 1.02 ± 0.37, N = 7 Stress, p < 0.0001).

G. Gain/loss of clustered dendritic spines. Two-way ANOVA: stress x clustered dynamic F_1,22 = 32.45, p < 0.0001 post-hoc Tukey test: control vs stress groups for gains p = 0.0007 for losses p = 0.012, N = 7 stress, 6 control mice.

H. Gain/loss of dendritic mitochondrial coverage. Two-way ANOVA: stress x mitochondrial remodeling F_1,22 = 20.37, p = 0.0002 post-hoc Tukey test: control vs stress for gains p = 0.013 for losses p = 0.03, N = 7 stress, 6 control mice.

I. Effect of stress on the net change of mitochondrial coverage and spine density. Student two-tailed T-test comparing control and stress groups for the mitochondria *p = 0.0005 and spines *p = 0.001, N = 7 stress and 6 control mice.

J. Pearson correlation between the net change of spine density and mitochondria coverage.