TABLE.

Summary of Assumptions for Consistent Estimation

	Assumption	Consequences of Violation	Example of Violation	Possible Solution(s)
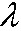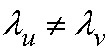1	There is a constant incidence rate () across time within each treatment arm (but it may differ across treatment arms due to vaccine effect, )	The prevalence odds will no longer be proportional to the product of incidence and mean duration. The transmission probability will no longer be proportional to the product of the mean duration time and the mean infectiousness in the sample. Equations 3–5 fail.	(1) If the epidemic is growing or waning in the communities in which the trial is conducted. (2) If 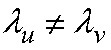then prevalence odds in vaccinated will reflect a mix of incidence before and after the vaccine took effect.	Use outside information to adjust distributions for epidemic trajectory. Estimates at different time points in an outbreak could be useful for other communities with similar epidemics.
2	Vaccination status does not affect probability of contact with susceptible individual at any time point	Probability of transmission is no longer proportional to the product of the probability of infection, the mean duration of infectiousness, and the mean infectiousness given contact. Equations 3–5 fail.	(1) If vaccination reduces the probability of symptoms given infection and symptomatic patients are less likely to contact other individuals. (2) If vaccinated individuals increase risky behavior in a rollout or if there is unblinding in a trial. (3) In a rollout or cluster randomized trial, if vaccinated individuals are more likely to come into contact with other vaccinated individuals rather than unvaccinated susceptible individuals.	If the effect is through an effect on symptoms or another measured covariate, the infectiousness function can be adjusted. This estimate might distinguish the vaccine efficacy measured in an individual randomized controlled trial from the vaccine effectiveness seen in a cluster randomized controlled trial or a real-world rollout.
3	Undetectable individuals are un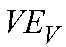infectious	no longer measures vaccine efficacy against being infectious. Equation 5 fails.	Low test sensitivity.	Might be able to adjust if sensitivity is known, but need to account for relative infectiousness of undetectable individuals.
4	Vaccination affects per-contact infectiousness only through the measured viral load (and other measured covariates), via. a known function or functions	Comparison of viral loads no longer estimates 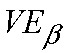. Equation 6 fails.	(1) If vaccination reduces the likelihood of being symptomatic at each viral load level and symptomatic patients have higher infectiousness per contact. (2) If viral load measured at a point in time is an inaccurate summary of mean viral load and the infectiousness function does not correctly account for this mismeasurement. (3) If the relationship between viral load and infectiousness is unknown or mismeasured, or the effect of vaccination on this relationship is unknown.	If it affects a covariate (e.g., symptom status) that is measured in the sample, then the infectiousness functions can be specified conditional on the covariate. Can use hypothesized relationships to get bounds on 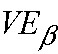. Can conduct sensitivity analyses with other possible relationships.