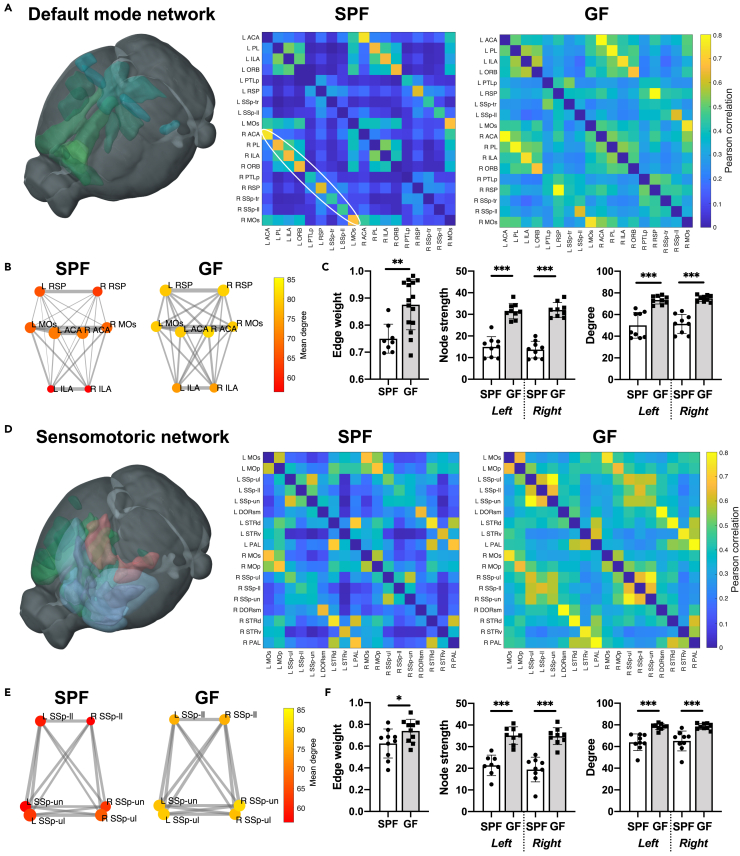
Figure 2.

Germ-free mice with increased functional connectivity in the default mode and sensorimotor network

(A) 3D-illustration of brain regions related to the default mode network (DMN) (represented by the regions ACA, PL, ILA, ORB, PTLp, RSP, SSp-tr, SSp-ll, and MOs). The adjacency matrices present the Pearson correlation values for the related regions in the SPF and GF group.

(B) Graph representation of intra- and interhemispheric connectivity between a subset of DMN regions. Circle color represents mean degree. The edge weight line thickness was scaled 0-1 and the node size represents the node strength.

(C) Quantitative comparison of edge weight, node strength and degree for DMN regions (Student's t test and two-way ANOVA with FDR correction for multiple comparisons). Edge weight calculated for homotopic connections only (e.g., Left ACA – Right ACA), node strength and degree reported for left and right hemisphere separately.

(D) 3D-illustration of brain regions related to the sensorimotor network (SMN) (represented by the regions MOp, MOs, SSp-ul, -ll, -un, DORsm, DORpm, STRd, STRv, and PAL). The adjacency matrices present the Pearson correlation values for the related regions in the SPF and GF group.

(E) Graph representation of intra- and interhemispheric connectivity between a subset of SMN regions SSp-ll/-ul/-un. Circle color represents mean degree. The edge weight line thickness was scaled 0-1 and the node size represents the node strength.

(F) Quantitative comparison of edge weight, node strength, and degree for SMN regions (Student's t test and two-way ANOVA with FDR correction for multiple comparisons). Edge weight calculated for homotopic connections only (e.g., Left SSp-ul – Right SSp-ul), node strength and degree reported for left and right hemisphere separately.

Data are represented as an adjacency matrix with mean values across groups, and bar plots with individual data points, mean and SD. SPF n = 8, GF n = 15.