Skip to main content
. Author manuscript; available in PMC: 2022 Oct 1.
Published in final edited form as: Epilepsia. 2021 Jul 29;62(10):2372–2384. doi: 10.1111/epi.17025

Figure 2. Tractography-based source localization of interictal spikes.

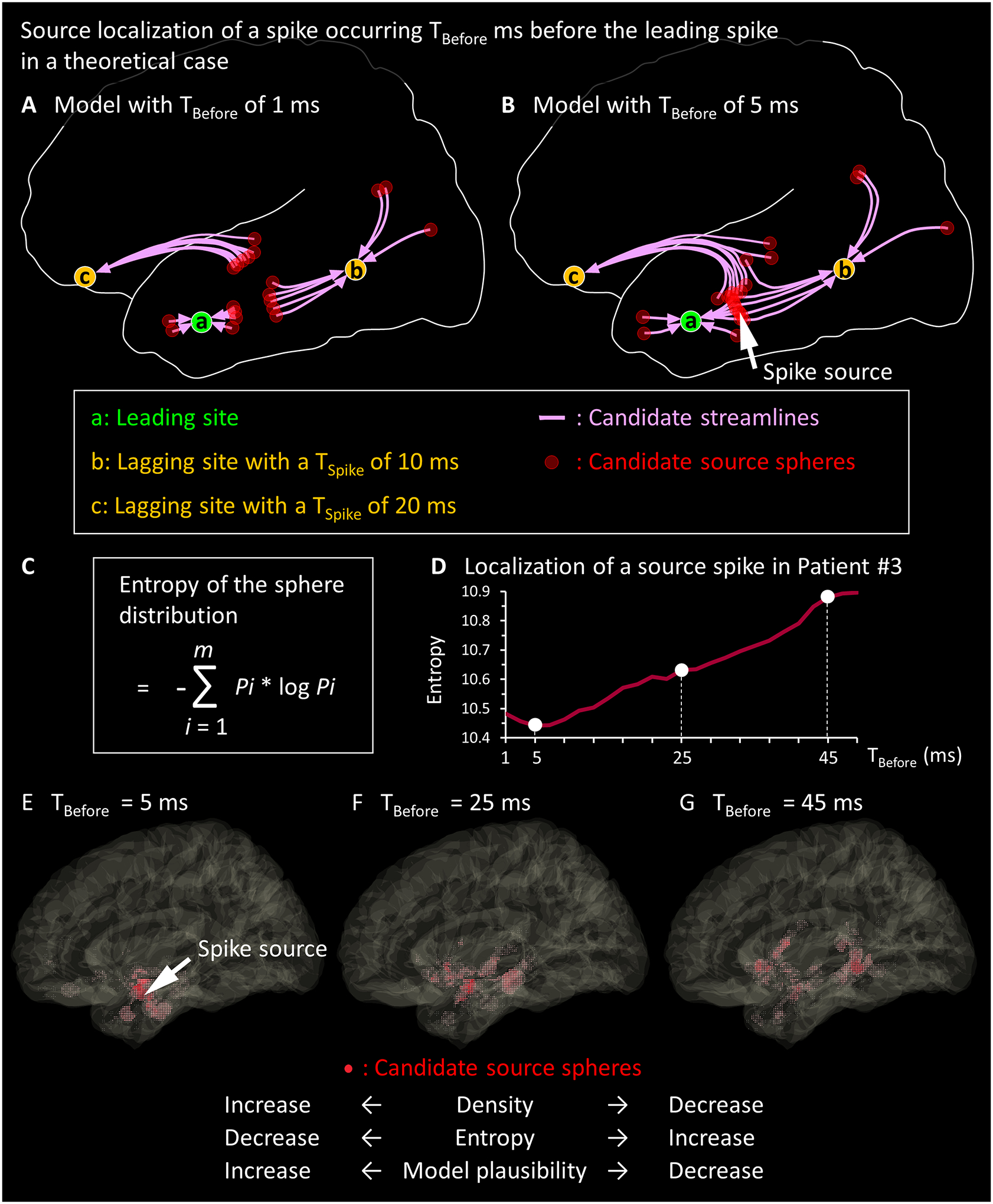
Figure 2.

(A-B) The schematic illustrations present the concept of our tractography-based source localization in a scenario where Channel [a] is the leading site, Channel [b] is a lagging site with a spike latency (TSpike) of 10 ms, and Channel [c] is a lagging site with a TSpike of 20 ms. (A) The model with TBefore of 1 ms results in a scarce spatial distribution of ‘candidate source spheres’; thus, none of the resulting spheres plausibly induce spike propagations at these lagging sites at given observed latencies. (B) The model with TBefore of 5 ms results in the densest distribution of ‘candidate source spheres’; the spike source will comprise the center of gravity of spheres (arrow). The source is estimated to be located where the spike would occur 5 ms before the leading site does. This model indicates that the spike would propagate from the source to the leading site in 5 ms. (C) The formula to compute the entropy of the sphere distribution is presented. Thereby, m is the total number of 1-mm voxels consisting of the entire space occupied by all spheres delineated with a given TBefore. Pi is [the number of candidate source spheres directly affecting the i-th voxel] divided by [the total number of voxels included in all spheres]. (D-G) The empirical data from a spike event observed in Patient #3 is presented. (D) The relationship between the TBefore and the entropy of sphere distribution is shown. (E) TBefore of 5 ms achieved the minimum entropy of the sphere distribution; in other words, the densest distribution of spheres (red shaded areas) was achieved at a focal area. The arrow denotes the estimated source of this spike discharge. Since the VProxy was found to be 1.46 ms in the present study, the spike source was suggested to be 7.3 mm (i.e., 1.46 × 5) away from the leading site. TBefore of (F) 25 ms or (G) 45 ms failed to achieve a unifocal distribution of spheres; thus, we considered these latencies less plausible than 5 ms for localizing the spike source.