Cope with the COVID-19 pandemic: Dynamic bed allocation and patient subsidization in a public healthcare system

Abstract

In many countries and territories, public hospitals play a major role in coping with the COVID-19 pandemic. For public hospital managers, on the one hand, they must best utilize their hospital beds to serve the COVID-19 patients immediately. On the other hand, they need to consider the need of bed resources from non-COVID-19 patients, including emergency and elective patients. In this work, we consider two control mechanisms for public hospital managers to maximize the overall utility of patients. One is the dynamic allocation of bed resources according to the evolution process of the COVID-19 pandemic. The other is the usage of a subsidy scheme to move elective patients from the public to private hospitals. We develop a dynamic programming model to study the allocation of isolation and ordinary beds and the effect of the subsidy policy in serving three types of patients, COVID-19, emergency, and elective-care. We first show that the dynamic allocation between isolation and ordinary beds can provide a better utilization of bed resources, by cutting down at least 33.5% of the total cost compared with the static policy (i.e., keeping a fixed number of isolation beds) when facing a medium pandemic alert. Our results further show that subsidizing elective patients and referring them to private hospitals is an efficient way to ease the overcrowded situation in public hospitals. Our results demonstrate that, by dynamically conducting bed allocation and subsidy scheme in different phases of the COVID-19 pandemic, patient overall utility can be greatly improved.

1. Introduction

The coronavirus disease 2019 (COVID-19) has struck the world in a fast speed, affecting 222 countries, areas or territories in months; until December 31, 2020, there have been 80, 773, 033 confirmed cases (WHO 2020a). In coping with the COVID-19 pandemic, public hospitals play a major role in many counties and territories. For example, in Hong Kong (HK), COVID-19 patients are only treated by public hospitals appointed by the government. The public hospital managers are facing a significant challenge. On the one hand, with a surging number of COVID-19 patients, they are facing massive shortages of isolation beds with a negative pressure environment. In particular, the isolation beds are set at negative pressure; this aims to prevent airborne microorganisms from entering corridors, which can result in secondary infections (The U.S. Centers for Disease Control and Prevention, 2019). On the other hand, they still need to consider the need from the non-COVID-19 patients with other diseases such as cancer and leukemia. During the pandemic period, many non-COVID-19 patients, particular those emergency ones, still require hospitalization in public hospitals. How to optimally allocate the limited amount of hospital beds between COVID-19 and non-COVID-19 patients is a very critical management problem.

The inpatient beds for two types of patients are different. Since COVID-19 is very contagious, the average number of new infections generated by an infected patient, i.e., the mean of reproductive number R ₀, is ranged from 1.4 to 6.5 (WHO 2020b; Park et al., 2020). Thus, to avoid cross-infection in a healthcare facility, the COVID-19 patients must be provided with the isolation beds under a negative pressure environment. In contrast, non-COVID 19 patients only need ordinary beds. Two types of beds (i.e., isolation and ordinary beds) need to be separately prepared to satisfy different demands from COVID-19 and non-COVID-19 patients. The two types of beds can be transformed into each other, after taking certain steps of modification work. In this work, we not only consider the bed reservation issue on two types of beds, but also consider the transformation possibilities between them. Different types of patients have different urgency levels on bed request. To prevent further spread of coronavirus, the adequate capacity of isolation beds should be prepared so that confirmed COVID-19 patients can be admitted immediately. The non-COVID-19 patients can be further divided into two classes, emergency non-COVID-19 patients (hereafter referred to emergency patients) and elective non-COVID-19 patients (hereafter referred to elective patients). The emergency patients must be admitted immediately upon their arrival, while the elective patients can wait. Therefore, ordinary beds shall be first allocated for emergency patients and the extra ones can be used to admit elective patients.

Upon the outbreak of COVID-19, the surging number of COVID-19 patients can cause big pressure to the public hospitals and elective patients are often been put on waiting list. For example, millions of operations in the UK had been postponed by NHS to tackle the COVID-19 pandemic (The Guardian, 2020), and reducing elective surgery is one of essential manners to utilize the limited medical capacity (7NEWS, 2020). Waiting in the queue can cause a deterioration in patients’ health condition and a waiting cost is incurred for them. Therefore, besides serving the COVID-19 patients and emergency patients, reducing waiting time for elective patients is also a key issue for the public hospital managers. One effective way to reduce the waiting line is to subsidize elective patients and refer them to private hospitals for treatment. Even without pandemic, the subsidy mechanism has been widely adopted to relieve the pressure of the public hospitals by many countries and areas such as England, Australia and Hong Kong; see Qian et al. (2017), Guo et al. (2019). There are multiple merits by conducting this mechanism during the COVID-19 pandemic. One, elective patients can obtain faster treatment in private hospitals, without worrying about the expensive payment and the infection from COVID-19. Two, the overcrowded situation in public hospitals can be eased and the bed resource can be utilized to cope with the COVID-19 patients. Three, private hospitals may face a thinned patient flow in the pandemic period because some of their regular patients are afraid of going to hospitals during pandemic. It is good for them to serve these subsidized patients, even with some price discounts. Indeed, between late February and April 15, 2020, the Hong Kong government subsidized part of non-COVID-19 patients, e.g., 66 babies, 5 cancer patients, and 15 pregnant women, and referred them to private hospitals for treatment (Cheung, 2020). However, subsidy scheme is not perfect because the government budget is limited and governments have to adopt some requirements on patients so that the subsidy is appropriately applied; see Qian et al. (2017) for the discussions of pros and cons of different types of subsidy schemes. We do not consider the detailed format of subsidy scheme here but instead we consider a general cost function associated with the number of subsidized patients. The policy makers concern about the following question: how many elective patients in public hospitals should be subsidized and be referred to the private hospitals during different phases of the COVID-19 pandemic?

Our work is motivated by healthcare operations (i.e., capacity planning) to cope with the most recently COVID-19 pandemic. However, our model and analysis are not restricted to manage the pandemic created by COVID-19 from an operational perspective. In this work, we aim to investigate the effectiveness of a dynamic scheduling rule for serving three types of patients in different phases of the pandemic. The utilization of bed capacity is a key factor that impacts the effectiveness of the dynamic bed allocation and waiting list management. In this context, we explore how a hospital manager's operational decisions (i.e., bed allocation and patient subsidization) impact the total cost of the public healthcare system. We develop a dynamic programming model to find optimal decisions on bed allocation and patient subsidization in different periods, by considering evolution processes of the COVID-19 pandemic.

Compared with the literature, our dynamic programming model has the following unique features. First, we take a more holistic approach by jointly considering the hospital beds allocation and waiting list management while past studies consider these two problems separately. Second, we consider three types of patients (COVID-19, emergency and elective patients) in our study while past studies normally consider two types (emergency and elective patients). Furthermore, the arrival processes of different type of patients are time-dependent, while they are often stationary in the past studies. This time-dependence feature is driven by the evolution process of pandemic and its big impact on patients’ behavior. In reality, WHO adopts a six-phased approach to illustrate the evolution process of pandemic and make response plans (WHO, 2009). We mainly consider two phases, namely outbreak and post-peak phases. Our outbreak phase is corresponding to WHO phases 5–6, during which an increasing number of COVID-19 patients are presenting at public hospitals and the elective patients are decreasing because they are worrying about infection from the pandemic (Mafham et al., 2020). Thus, arrival processes of COVID-19 and elective patients present a negative correlation in this phase. In the post-peak phase, arrival processes of COVID-19 patients and elective patients has downward and upward trends, respectively, and public hospitals should also prepare for a possible second wave. Third, our bed allocation decision considers two types of bed reservation issues: ordinary and negative-pressure beds. Furthermore, we not only consider the bed reservation problem but also consider the converting between the ordinary and the isolation beds. This type of exclusive consideration can provide a better utilization of bed resource.

Our results are helpful for hospital managers. First, we demonstrate the multimodularity of the total expected cost function on the number of reserved isolation beds and the length of waiting list. We show that a longer waiting list makes it harder to reserve more isolation beds. Second, we prove that our dynamic allocation rule can provide a better utilization of isolation and ordinary beds in different phases of a pandemic disease, especially in saving the total cost compared with the static policy (i.e., keeping a fixed number of isolation beds). We also find that our dynamic allocation policy works best under conditions when a region facing a medium pandemic situation and it can reduce the cost of the static policy by at least 33.5%. Third, our results show that subsidizing elective patients and referring them to private hospitals is an efficient way to ease the overcrowded situation in public hospitals. Specifically, by comparing the experiment outcomes with and without a subsidy scheme, we show that a subsidy-scheme can reduce the total cost by 38% and shorten the queue length by 58%. We also find that the cost saving effect of a subsidy scheme is convex in the hospital bed capacity. In short, these useful results are critical to hospital managers for determining the best strategies for serving multiple types of patients through the course of a pandemic.

The remainder of this paper is organized as follows. The related literature is reviewed in Section 2. We introduce the model setting by considering the epidemiology features of the COVID-19 pandemic in Section 3. And the research problem is formulated as a finite-horizon Markov decision process. In Section 4, we analyze the structure properties of dynamic programming model, that establishes fundamental insights on the optimal scheduling rule. In Section 5, we analyze optimal decisions in different phases of the COVID-19 pandemic. In Section 6, we provide various numerical examples to validate our analytical results. And we summarize key results and discuss implications of these results in Section 7. All proofs can be found in Appendix A.

2. Literature review

This paper focuses on analyzing the dynamic hospital bed allocation and patient subsidization to cope with pandemic diseases, which contributes to the following three streams of the literature. Interested readers also can refer to Keskinocak and Savva (2020) for more comprehensive and the latest review about the research opportunities of healthcare management (modeling).

2.1. Hospital bed allocation

Several studies have investigated hospital bed allocation issue in normal circumstances. Astaraky and Patrick (2015) formulate a dynamic programming model to study the surgical scheduling issue by considering the multi-class patients and two types of resources (i.e., operating rooms and recovery beds). The Least Squares Approximate Policy Iteration algorithm is developed to validate analytical results and proposed operational policy. Besides, Best et al. (2015) explore a hospital manager's optimal decisions to allocate bed capacity: the number of wings to form and the number of beds to allocate to each wing. Kilinc et al. (2016) study the dynamic assignment of Emergency Department admitted two types of patients: primary and secondary patients. However, Kilinc et al. (2016) do not consider the effect of the time-varying discharge as we have incorporated this feature in our model. More recently, Lee et al. (2021) propose a coordination mechanism via a fork-join queueing system to reduce delays in bed allocation for emergency department patients. Li et al. (2021) investigate capacity reallocation in a hierarchical medical system with high- and low-level types of hospitals. They develop two payments schemes to coordinate capacity sinking. Research work described above mainly focus on a single type of ordinary inpatients bed; in contrast, we consider two types of beds, i.e., isolation and ordinary beds, which can be transformed into each other to satisfy the demands from COVID-19, elective, and emergency patients.

2.2. Infectious disease management

Our work is related to the literature on infectious disease management. The allocation of scarce resources is a key issue to cope with pandemic diseases, e.g., SARS, MERS, H1N1, and COVID-19. For example, Mamani et al. (2013) examine a contractual mechanism to increase vaccine supplies in advance of seasonal influenza rather than in response to a pandemic. Ekici et al. (2014) develop a facility location and resource allocation model to analyze food distribution when facing a severe influenza pandemic. Deo and Sohoni (2015) build an optimization model to study the allocation of point-of-care HIV diagnostic devices to mitigate the potential of long diagnostic delays. Long et al. (2018) formulate an optimization model to forecast the occurrence of new infections and to analyze spatial resource allocation. More recently, there are plenty of reports and studies on the COVID-19, mainly published in medical journals. In the operations management field, Kaplan (2020) develops scratch models to support their local community decisions to cope with the outbreak of the COVID-19 pandemic. Kaplan (2020) considers multiple measures on bed reservation and also mentions the converting from ordinary beds into isolation beds. However, Kaplan (2020) does not provide a dynamic decision of the resource allocation as we have done in our work.

2.3. Capacity planning in healthcare management

Our work is also related to capacity planning in a healthcare system, e.g., Green et al. (2006), KC and Terwiesch (2012), Kim et al. (2015). For example, Patrick et al. (2008) study a dynamic capacity allocation problem for patients with different priories in a public hospital. To reduce waiting time in a cost-effective manner, they proposed the approximate optimal policy based on the analytical results of an approximate dynamic programming. The threshold for the amount of overtime is identified that can assist the resource manager make daily allocation decisions. Dai and Shi (2019) investigate the problem of inpatient overflow by introducing a multi-class, multi-pool parallel-server queueing system. The overflow decision is formulated as an average-cost Markov decision process. Our work differs from this stream in two aspects. First, previous studies examine the optimal decisions of a single type of medical resources, e.g., hospital diagnostic facilities, intensive care unit capacity, and staff. Our work instead considers two types of hospital beds. Specifically, we investigate isolation beds reservation given the limited capacity and the transformation possibilities between two types of beds during different phases of the COVID-19 pandemic. Second, previous studies assume patients arrive according to a stochastic process, e.g., a Poison process, that is exogenous and independent of the current state of the system, see, Samiedaluie et al. (2017), and Liu et al. (2019). For example, Liu et al. (2019) focus on allocating a single resource to admit elective and emergency patients; they also assume capacity usage in two successive stages are independent. In contrast, we consider two arrival settings for the COVID-19 and elective patients, which are assumed to be time-dependent according to the epidemiology features of the COVID-19 pandemic. We also consider using isolation and ordinary beds separately to admit COVID-19 and non-COVID-19 patients; besides, these two types can be transformed into each other in the outbreak and post-peak phases. In our model, due to the existence of COVID-19 patients, the capacity planning has to consider infection among patients, and hospital beds have to be separated into two types, which is more challenging in analysis.

3. The model

In this section, we describe the model setting of a discrete-time dynamic programming model and introduce notation used throughout the paper. We consider the allocation of the limited medical capacity, i.e., isolation and ordinary beds, to admit both COVID-19 and non-COVID-19 patients in a finite time horizon t, where t = 1, …, T. The summary of notation used in our paper is attached in Appendix B.

Demands of COVID-19, emergency, and elective patients over a period t are nonnegative integer-valued random variables, denoted by ε _t, λ _t, and δ _t, respectively, where ${\epsilon }_t,{\lambda }_t,{\delta }_t\in \mathbb{Z}$ ($\mathbb{Z}$ denotes the set of nonnegative integers). We assume the demand of emergency (non-COVID-19) patients, λ _t, is an independent and identically distributed (i.i.d.) random variable for t = 1, …, T. In reality, all inpatients stay in the public system for a random number of days before being discharged from the public system. We assume random fractions ${\xi }_t^c$ and ${\xi }_t^n$ of COVID-19 and non-COVID-19 inpatients exit the public system at the end of period t, respectively, where ${\xi }_t^j\in (0,1)$ and ${\xi }_t^j$ is i.i.d. for j ∈ {c, n}. This assumption is in line with the literature, for example, Liu et al. (2019).

We denote by x _t the number of available ordinary beds at the beginning of period t, after non-COVID-19 inpatients discharged from the public system; y _t the number of reserved isolation beds (created in a negative pressure environment) for serving COVID-19 patients. Let w _t be the number of elective patients on the waiting list to receive public healthcare. The triplet (x _t, y _t, w _t) is the vector of state variables observable before any decision made in period t.

3.1. The dynamic of flow

In our model, the arrival processes of COVID-19 and elective patients are assumed to be time-dependent according to the epidemiology features of COVID-19 pandemic. Both COVID-19 patients and emergency patients are admitted immediately, whereas elective patients should join a waiting list if ordinary beds are unavailable. Meanwhile, to relieve the congested public health care system, elective patients can be removed from the waiting list by being offered with a financial subsidy. The patient flow, bed transformation and allocation are illustrated in Fig. 1 .

Fig. 1.

The illustration of patient flow and bed allocation.

In each period, the decisions of the hospital manager are summarized as follows: (1) the hospital manager needs to reserve a number of isolation beds, n _1,t, to cope with COVID-19 patients, and allocate some of ordinary beds, n _2,t = x _t − n _1,t, to admit non-COVID-19 patients; (2) the hospital manager decides to remove a number of elective patients, n _3,t, with a financial subsidy; (3) the hospital manager decides to transform some of excessively reserved isolation beds into ordinary beds, n _4,t, to admit elective patients, especially in the post-peak period. In summary, there are three decision variables for the manager, (n _1,t, n _3,t, n _4,t). As it is not cost-efficient to reserve the isolation beds and reallocate the reserved isolation beds to admit non-COVID-19 patients simultaneously, n _1,t ⋅ n _4,t = 0 in any period t.

The sequence of events in any period is summarized as follows.

• 1.At the beginning of period t, there are w _t elective patients on the waiting list and a waiting cost M _t(w _t) is incurred. We assume M _t(w _t) is an increasing convex function of the queue length, which is in line with the literature, for example, Mandelbaum and Stolyar (2004). The hospital manager obtains the number of available isolation and ordinary beds, y _t and x _t, respectively.
• 2.The hospital manager retrofits a number of ordinarily beds n _1,t into isolation beds to admit COVID-19 patients. The unit retrofitting cost is denoted as c _b. The remaining capacity, n _2,t = x _t − n _1,t, can be allocated to admit non-COVID-19 patients, with emergency patients to be served first. The unit treatment cost for admitting a non-COVID-19 patient is denoted by c _n. If isolation beds are excessively reserved, the manager needs to determine how many of them, n _4,t, can be transferred back to ordinary beds to serve non-COVID-19 patients. The unit transferring cost is denoted as c _d.
• 3.The number of COVID-19 patients, emergency patients, and elective patients, represented by (ε _t, λ _t, δ _t), is realized. The COVID-19 patients must be admitted immediately using the reserved isolation beds, y _t. And non-COVID-19 patients are allocated with the available ordinary beds, n _2,t. New incoming elective patients join the waiting list if there is no available beds for them. If too many non-COVID-19 patients are admitted, the limited isolation beds are unable to meet the demand of COVID-19 patients, which may cause big hazard for the society. We denote c _p as the unit penalty cost for the public hospital if COVID-19 patients cannot be served immediately. If too few non-COVID-19 patients are admitted, the waiting time of elective patients increases. Besides, if the excessively reserved isolation beds cannot be fully utilized, this is a waste of medical resource. There is an idling cost, c _o, inured for each reserved isolation bed. At the end of a period, we denote by F _t(y _t, w _t) the penalty/idling and waiting costs, where F _t(y _t, w _t) = L _t(y _t) + M _t(w _t) and $L_t(y_t)=c_p{y}_t^{-}+c_o{y}_t^{+}$, where x ⁻ = min(0, x), x ⁺ = max(0, x). Recall that we do not consider the penalty cost for unmet emergency non-COVID-19 patients because there are normally multiple public hospitals and, if one hospital capacity is full, the emergency patient will be sent to another hospital via ambulance diversion (Allon et al., 2013).
• 4.If the waiting list is too long, the manager can offer a financial subsidies, c _s(n _3,t), to some elective patients who can then be referred to private hospitals for treatment. This subsidy cost function is assumed to be increasing and convex in the number of subsidized elective patients n _3,t. The subsidy discipline is first-come-first-serve, which prioritizes patients based on their arrival times.
• 5.At the end of period t, the COVID-19 and non-COVID-19 patients are discharged from the public hospital with random proportions ${\xi }_t^c$ and ${\xi }_t^n$, respectively, where ${\xi }_t^j\in (0,1),j\in \{c,n\}$. Emptied beds are cleaned following cleaning and disinfecting procedures before admitting new patients. This is a common setting in literature, e.g., Liu et al. (2019).

The objective of the hospital manager is to identify a bed reservation rule and financial subsidy rule for elective patients, to minimize the overall cost of the whole system, including the total operations cost over the planning horizon and patient waiting cost.

3.2. Dynamic programming formulation

We now formulate the manager's decision problem as a Markov decision process (MDP). Based on the above analysis, we consider a finite planning horizon of T periods. The hospital manager reviews the system states and makes decisions in each period. The dynamic of states observed at the beginning of period t evolves into period t + 1 are formulated as follows.

The state of COVID-19 patients evolves following the equation:

$${\epsilon }_{t+1}={\alpha }_c{\epsilon }_t+u_t,$$ (1)

where the coefficient α _c indicates reproduction of COVID-19 patients in different phases of pandemic alert, and u ₁, …, u _T are independent random variables representing the noisy terms of ε _t with mean zero. As discussed in the introduction, we denote by α _c > 1 to describe the widespread human infection in outbreak phase, and denote by α _c < 1 to represent the post-peak phase with few infections. We use this to capture the reproduction number of COVID-19 and this is a common setting in the field of mathematical epidemiology, see Lloyd-Smith et al. (2005), Diekmann and Heesterbeek (2000).

The number of COVID-19 patients in the system is updated by:

$$l_{t+1}^c=(1-{\xi }_t^c)l_t^c+{\epsilon }_t,$$ (2)

on the right hand-side of Eq. (2), the first term is the number of COVID-19 patients in the system after discharging in period t; the second term is the noisy terms of COVID-19 patients.

The state of reserved isolation beds evolves following the equation:

$$y_{t+1}=y_t+{\xi }_t^c{l}_t^c-{\epsilon }_t+n_{1,t}-n_{4,t},$$ (3)

on the right hand-side of Eq. (3), the first term is number of reserved isolation beds in period t; the second term is emptied isolation beds after COVID-19 patients discharging from the hospital; the third term is the noisy terms of COVID-19 patients; the fourth term is number of reserved isolation beds used to admit COVID-19 patients in period t; the last term is the number of isolation beds transformed back into ordinary beds in period t.

For elective patients, the state evolves following the equation:

$${\delta }_{t+1}={\alpha }_n{\delta }_t+k_t,$$ (4)

where the coefficient α _n indicates newly generated elective patients in different phases of pandemic alert, and k ₁, …, k _T are independent random variables representing the noisy terms of δ _t with mean zero. Fearing cross-infections in the public hospital, elective patients may choose to wait, especially in outbreak period, and opt for public healthcare in the post-peak period. Thus, we denote by α _n < 1 to show outbreak phase, and denote by α _n > 1 to represent the post-peak phase.

The number of non-COVID-19 patients in the system is updated by:

$$l_{t+1}^n=(1-{\xi }_t^n)l_t^n+{\lambda }_t+\min \{{(n_{2,t}+n_{4,t}-{\lambda }_t)}^{+},w_t\},$$ (5)

on the right hand-side of Eq. (5), the first term is the number of elective patients in the system after discharging in period t; the second term is the newly arrived elective patients in period t; the third term is the number of available ordinary beds used to admit elective patients.

The number of available ordinary beds in the system is updated by:

$$x_{t+1}=x_t+{\xi }_t^n{l}_t^n-n_{1,t}-n_{2,t},$$ (6)

on the right hand-side of Eq. (6), the first term is number of ordinary beds in period t; the second term is emptied ordinary beds after elective patients discharging from the hospital; the third term is the number of retrofitted ordinary beds into isolation beds in period t; the last term is the number of ordinary beds allocated to serve non-COVID-19 patients in period t.

The state of elective patients on the waiting list evolves following the equation:

$$w_{t+1}={(w_t+{\delta }_t-{(n_{2,t}+n_{4,t}-{\lambda }_t)}^{+}-n_{3,t})}^{+},$$ (7)

on the right hand-side of Eq. (7), the first term is number elective patients on the waiting list in period t; the second term is newly arrived elective patients in period t; the third term is the maximum number of admitted elective patients in period t, the last term is the number of subsidized elective patients form the waiting list in period t.

In line with the literature in healthcare management, we aim to minimize total cost to reduce wait-time and improve utilization of medical capacity in a cost-effective manner (Patrick et al. (2008), Astaraky and Patrick (2015), Dai et al. (2019)). Let V _t(x _t, y _t, w _t, d _t) be the total discounted cost incurred from periods t to T given the state variables (x _t, y _t, w _t, d _t), where d _t denotes the nonnegative vector consisting of ε _t, λ _t, and δ _t. Thus, the Bellman equation can be established as follows:

$$\begin{array}{cc}& V_t(x_t,y_t,w_t,{\mathbf{d}}_t)={\min }_{\begin{array}{c}{n}_{1,t},n_{2,t},\\ n_{3,t},n_{4,t}⩾0\end{array}}\left\{c_b{n}_{1,t}+c_n{n}_{2,t}+c_s(n_{3,t})+c_d{n}_{4,t}+\mathbb{E}{F}_t\left(y_t-{\epsilon }_t+n_{1,t}^c-n_{4,t}\right)\right)\\ & \left(\left(+{\xi }_t^c{l}_t^c,w_t+{\delta }_t-{(n_{2,t}+n_{4,t}-{\lambda }_t)}^{+}-n_{3,t}\right)+\gamma \mathbb{E}{V}_{t+1}(x_{t+1},y_{t+1},w_{t+1},{\mathbf{d}}_{t+1})\right\}\end{array}$$ (8)

where n _2,t = x _t − n _1,t, the expectation is taken over random variables, and the termination function V _T+1 = 0. Note that on the right hand side of Eq. (8), the first term in the brackets, c _b n _1,t, is the cost of retrofitting ordinary beds as isolation beds to cope with COVID-19 patients in period t; the second term, c _n n _2,t, is the treatment cost by admitting non-COVID-19 patients using ordinary beds in period t; the third term, c _s(n _3,t), is the financial subsidy offered to remove elective patients; the fourth term, c _d n _4,t, is the transferring cost by using the reserved isolation beds to serve non-COVID-19 patients; the fifth term, $\mathbb{E}{F}_t(\cdot ,\cdot )$, is the expectation of penalty/idling and waiting costs; the last term, $\gamma \mathbb{E}{V}_{t+1}(\cdot ,\cdot ,\cdot ,\cdot )$, is the minimum expected total discounted cost from period t + 1 to T.

In the following sections, we first analyze the structure properties of this problem and then find the optimal decisions on patient admission, bed allocation and waiting list reduction. We also conduct sensitivity analysis to provide some managerial insights.

4. Structure properties analysis

In this section, we examine the characteristics of the total expected cost function in Eq. (8). In our study, we adopt modularity analysis to obtain some structure properties of our decision problem. We first provide definitions and preliminaries analysis of modularity. Interested readers can refer to Topkis (1998), Murota (2005), and Li and Yu (2014) for comprehensive introduction of modularity analysis and its properties.

A partially ordered set X = {x’, x”} that contains the join (x′ ∨ x″) and the meet (x′ ∧ x″) of each pair of its elements is a lattice. If X′ is a subset of a lattice X and X′ contains the join and the meet of each pair of elements of X′, then, X′ is a sublattice of X. Suppose that f(x) is a real-valued function on a lattice X. A function f(x) is submodular if f(x′) + f(x″)⩾f(x′ ∨ x″) + f(x′ ∧ x″). Similarly, if − f(x) is submodular, then f(x) is supermodular. If f(x) and g(x) are supermodular on X, then f(x) + g(x) is supermodular on X (Topkis 1998).

Let $X\in {\mathbb{R}}^n$ and $Y\in \mathbb{R}$ be polyhedral satisfying that the nonzero components of a _i are either consecutive ones or consecutive negative ones, where $X=\{\mathit{x}\in {\mathbb{R}}^n|{\mathbf{a}}_i\cdot \mathit{x}⩾b_i,i=1,\dots ,m\}$, $b_i\in \mathbb{R}$. A function f: $X\to \mathbb{R}$ is multimodular if g(x, y) = h(x ₁ − y, x ₂ − x ₁, …, x _n − x _n−1) is submodular on a lattice $S=\{(\mathit{x},y)\in {\mathbb{R}}^n\times \mathbb{R}|y\in Y,(x_1-y,x_2-x_1,\dots ,x_n-x_{n-1})\in X\}$. (i) Suppose that g(v) is multimodular, g(v) has increasing differences; (ii) if g(v, d) is multimodular in v, (ii) for any given d and D is a random variable, then $\mathbb{E}g(\mathit{v},D)$ is multimodular in v (Li and Yu 2014).

Proposition 1

Fort = 1, …, T, V _t(x _t, y _t, w _t) is increasing in w _t and jointly convex in (y _t, w _t).

Proposition 1shows that the optimal expected operations cost is greater if elective patients cannot be admitted to the public hospital but only waiting for treatment. Also, the convexity ofV_t(x_t, y_t, w_t) iny_timplies that increasing marginal effect of reserving one more isolation bed. Besides, the convexity ofV_t(x_t, y_t, w_t) inw_timplies increasing marginal effect associated with adding one more elective patient to the waiting list. The joint convexity implies that there exists a state status of (y _t, w _t) corresponding to a minimal cost-to-go function V _t.

Recall that we have three decision variables for each period. To obtain some structure properties of the optimal decisions, we take a sequential optimization approach on finding the optimal solutions of the three decision variables. First, the hospital manager determinesn_1,t, namely the number of isolation beds reserved for admitting COVID-19 patients. Second, the hospital manager determinesn_3,t, the number of elective patients subsidized from the waiting list andn_4,t, the number of excessively reserved isolation beds transferred back into ordinary bed for admitting non-COVID-19 patients. Following the backward induction, we first find the optimal subsidization and reallocation decisions given the reserved isolation beds in §4.1; and then we find the optimal number of isolation beds reserved for COVID-19 patients in §4.2.

4.1. Managing non-COVID-19 patients

Here, the hospital manager faces the decisions of managing elective patients reserved isolation beds. He can manage the ‘demand’ by subsidizing n _3,t patients and move them away from the waiting list. He can also manage the ‘supply’ by increasing the supply of the ordinary beds through transferring n _4,t isolation beds into ordinary beds. The optimal solutions can be recursively solved through the following Bellman equation, for t = 1, …, T,

$$\begin{array}{cc}{H}_t^{*}(x_t,y_t,w_t,{\mathbf{d}}_t)=& {\min }_{\begin{array}{c}0⩽n_{3,t}⩽w_t\\ 0⩽n_{4,t}⩽y_t\end{array}}\left\{c_s(n_{3,t})+c_d{n}_{4,t}+\mathbb{E}{F}_t\left(y_t-{\epsilon }_t-n_{4,t}+{\xi }_t^c{l}_t^c,w_t+{\delta }_t\right)\right)\\ & \left(\left(-n_{3,t}-n_{4,t}\right)+\gamma \mathbb{E}{V}_{t+1}(x_{t+1},y_{t+1},w_{t+1},{\mathbf{d}}_t)\right\},\end{array}$$ (9)

where the expectation is taken over random variables, and the termination function V _T+1 = 0. On the right hand side of Eq. (9), the term, c _s(n _3,t), is the financial subsidy offered to remove elective patients; the second term, c _d n _4,t, is the transferring cost by using the reserved isolation beds to serve non-COVID-19 patients; the third term, $\mathbb{E}{F}_t(\cdot ,\cdot )$, is the expectation of penalty/idling and waiting costs; the last term, $\gamma \mathbb{E}{V}_{t+1}(\cdot ,\cdot ,\cdot ,\cdot )$, is the minimum expected total discounted cost from period t + 1 to T.

Proposition 2

IfF_t(y_t, w_t) is multimodular in (y _t, w _t) and V _t+1 is multimodular in (y _t+1, w _t+1), we have $H_t^{*}(x_t,y_t,w_t)$ is multimodular in (y _t, w _t).

Proposition 2shows that the property of multimodularity can be preserved under the minimization operation of two decision variables, n_3,tandn_4,t, which also assures the increasing monotonicity of the optimal solutions$(n_{3,t}^{*},n_{4,t}^{*})$in state variablesy_tandw_t (Topkis 1998; Gong et al., 2014). This is quite reasonable: if the number of reserved isolation beds, y _t, is larger, then the manager shall subsidize more patients to move them to the private system (i.e., increasing $n_{3,t}^{*}$) and also it is more likely to transfer some isolation beds back into ordinary beds (i.e., increasing $n_{4,t}^{*}$). Also, if the waiting list, w _t, is longer, it is better for the manager to move away some patients from the waiting list and transfer some isolation beds back into ordinary beds.

The multimodularity property implies the joint convexity of$H_t^{*}$in (y _t, w _t). It also implies the diagonal dominance, i.e., $\frac{{\partial }^2{H}_t^{*}}{\partial y_t^2}\ge \frac{{\partial }^2{H}_t^{*}}{\partial y_t\partial w_t}\ge 0$ and $\frac{{\partial }^2{H}_t^{*}}{\partial w_t^2}\ge \frac{{\partial }^2{H}_t^{*}}{\partial y_t\partial w_t}\ge 0$. This shows that marginal impact on $H_t^{*}$ due to a unit increase on y _t is more sensitive to the change in itself than the change in w _t and similar explanation holds for the change in w _t. We shall investigate the influence of y _t and w _t on the dynamic allocation policy, which is discussed in §5.

4.2. Reserving isolation beds for COVID-19 patients

After obtaining the optimal demand- and supply-side decisions on managing elective patients, we now consider the optimal bed reservation decision for COVID-19 patients.

At the beginning of period t, non-COVID-19 patients are discharged from the public hospital system and the total number of ordinary beds, x _t, can then be obtained. The hospital manager needs to determine n _1,t, namely the number of ordinary beds to be retrofitted into isolation beds, to cope with COVID-19 patients. The remaining ordinary beds, $n_{2,t}={(x_t-n_{1,t})}^{+}$, will be first allocated for emergency non-COVID-19 patients and only the extra ones can be used to admit elective patients.

The optimality equation for t = 1, …, T can be written as follows,

$$V_t(x_t,y_t,w_t,{\mathbf{d}}_t)={\min }_{\begin{array}{c}0⩽n_{1,t}⩽x_t-{\lambda }_t\end{array}}\{c_b{n}_{1,t}+c_n(x_t-n_{1,t})+H_t^{*}(x_t,y_t+n_{1,t},w_t+{\lambda }_t-x_t+n_{1,t},{\mathbf{d}}_t)\},$$ (10)

where the expectation is taken over random variables. On the right hand side of Eq. (8), the first term in the brackets, c _b n _1,t, is the cost of retrofitting ordinary beds as isolation beds to cope with COVID-19 patients in period t; the second term, c _n(x _t − n _1,t), is the treatment cost by admitting non-COVID-19 patients using ordinary beds in period t; the last term, $H_t^{*}$, is the minimum cost obtained by increasing the supply of ordinary beds and subsidizing elective patients. We have the following property of the total expected cost function V _t.

Proposition 3

If$H_t^{*}(x_t,y_t,w_t)$is multimodular in (y _t, w _t), we have V _t is multimodular in (y _t, w _t) for any x _t ⩾ 0.

Propositions 2and3yield the following corollary.

Corollary 1

Fort = 1, …, T, V _t is multimodular in (y _t, w _t) for any x _t ⩾ 0.

This result establishes the existence of global minimizers forV_t. The multimodularity ofV_tshows that the marginal change on the total cost of reserving one more isolation bed is increasing in the waiting listw_t. This implies that a longer waiting list of elective patients makes it harder for the manager to reserve more isolation beds. In addition, when facing too many reserved isolation beds, the hospital manager can manage the ‘supply’ side by transforming isolation beds back into ordinary beds to admit more elective patients. flushleft

4.3. Monotonicity of optimal decisions

With the above properties of the Bellman equation, we analyze the detailed characterizations of the optimal decisions. Since it is not cost-efficient to reserve isolation beds and reallocate the reserved isolation beds simultaneously, we investigate the monotonicity of the optimal retrofitted ordinary beds into isolation beds $n_{1,t}^{*}$ to cope with COVID-19 patients. To achieve efficient allocation and patient admission with the minimum total cost, we then analyze the impacts of number of elective patients on waiting list, w _t, and reserved isolation beds, y _t, on the manager's optimal subsidization and reallocation decisions ($n_{3,t}^{*}$ and $n_{4,t}^{*}$). The results are summarized in the following propositions.

Proposition 4

Fort = 1, …, T, suppose (x _t, y _t, w _t, d _t) is the initial state in period t,

• (i)the optimal number of ordinary beds retrofitted into reserved isolation beds,$n_{1,t}^{*}$, is decreasing inw_tand increasing inx_t;
• (ii)the optimal number of ordinary beds allocated to admit non-COVID-19 patients,$n_{2,t}^{*}$, is decreasing inx_t;
• (iii)the optimal subsidized elective patients,$n_{3,t}^{*}$, and the optimal transformed of excessively reserved isolation beds into ordinary beds,$n_{4,t}^{*}$, are increasing iny_tandw_t.

Proposition 4 shows that the optimal decisions in beds allocation and waiting list management behave the monotonicity of state variables. First, the increasing monotonicity of $n_{1,t}^{*}$ in x _t implies that more isolation beds should be reserved in the outbreak phase; the decreasing monotonicity of $n_{1,t}^{*}$ in w _t indicates that, if a waiting list is longer, subsidizing elective patients and moving them away from the waiting list is cost-efficient. Second, as $n_{2,t}^{*}=x_t-n_{1,t}^{*}$ and $n_{1,t}^{*}$ is increasing in x _t, $n_{2,t}^{*}$ decreases in x _t. Third, as part (iii) shows, if the number of reserved isolation beds, y _t, is larger and the waiting list, w _t, is longer, it is better to transfer more isolation beds back into ordinary beds and also to use subsidy to remove more elective patients from the waiting list.

In the following section, we discuss the efficient control policy regarding bed reservation and patient subsidy. We also conduct the sensitivity analysis of optimal policy towards the state variables y _t and w _t.

5. Decision analysis and implications

By characterizing the properties of the objective function in Eq. (8), we are now ready to analyze the optimal decisions. Facing the limited bed capacity and the COVID-19 pandemic, the hospital manager should manage the situation from both demand- and supply-side. On the supply side, facing the surging demand of COVID-19 patients in the outbreak phase, the manager can retrofit some ordinary beds into isolation beds, especially in the outbreak phase. In the post-peak phase, the demand from COVID-19 patients is diminishing and the hospital manager can transfer excessively reserved isolation beds into ordinary beds. On the demand side, the manager can use subsidy to remove some elective patients from the waiting list. For both outbreak phase and post-peak phase, we conduct comparison analysis of two different decisions to investigate the optimal operational rule.

By Proposition 3, we learn that these decisions can be found recursively by solving the following equation, for t = 1, …, T,

$$V_t(x_t,y_t,w_t,{\mathbf{d}}_t)={\min }_{\begin{array}{c}0⩽n_{1,t}⩽x_t-{\lambda }_t\end{array}}\{c_b{n}_{1,t}+c_n(x_t-n_{1,t})+H_t^{*}(x_t,y_t+n_{1,t},w_t+{\lambda }_t-x_t+n_{1,t},{\mathbf{d}}_t)\},$$ (11)

where

$$H_t^{*}(x_t,y_t,w_t,{\mathbf{d}}_t)=\underset{n_{3,t},n_{4,t}⩾0}{\min }\{c_s(n_{3,t})+c_d{n}_{4,t}+h_t(y_t,w_t,x_t)\}$$

and

$$h_t(y_t,w_t,x_t)=\mathbb{E}{F}_t(y_t-{\epsilon }_t+{\xi }_t{l}_t,w_t)+\gamma \mathbb{E}{V}_{t+1}(x_{t+1},y_{t+1},w_{t+1},{\mathbf{d}}_{t+1}).$$

We discuss trade-offs of bed allocation and subsidization decisions in different phases of COVID-19 pandemic. For the outbreak phase, our decisions variables are n _1,t (or n _2,t) and n _3,t. Given state variables (x _t, y _t, w _t) in period t, the marginal cost of retrofitting an ordinary bed into an isolation bed to cope with COVID-19 patients is c _b + ∂h _t(x _t, y _t, w _t)/∂y _t. According to Lemma 1 (Li and Yu, 2014), c _b + ∂h _t(x _t, y _t, w _t)/∂y _t is increasing in y _t and w _t. The marginal cost of subsidizing an elective patients from the waiting list is c _s − ∂h _t(x _t, y _t, w _t)/∂w _t. To analyze the tradeoff between reserving isolation beds and subsidizing elective patients, we investigate the difference of these two marginal costs, which is c _b − c _s + ∂h _t(x _t, y _t, w _t)/∂y _t + ∂h _t(x _t, y _t, w _t)/∂w _t. This cost difference is increasing in y _t and w _t. Next, we define three curves in (y _t, w _t) plane to illustrate the optimization process. We use superscript ‘o’ to denote the marginal costs incurred in the outbreak phase.

$$\begin{array}{cc}& Y_t^o(w_t,x_t)=\sup \{y_t:c_b+\partial h_t(x_t,y_t,w_t)/\partial y_t<0\},\\ & W_t(y_t,x_t)=\inf \{w_t:c_s-\partial h_t(x_t,y_t,w_t)/\partial w_t<0\},\\ & Z_t^o(w_t,x_t)=\sup \{y_t:c_b-c_s+\partial h_t(x_t,y_t,w_t)/\partial y_t+\partial h_t(x_t,y_t,w_t)/\partial w_t<0\}.\end{array}$$

We adopt the same logic to analyze decisions made in the post-peak phase. For this phase, our decisions variables are n _3,t and n _4,t. Given state variables (x _t, y _t, w _t) in period t, the marginal cost of transferring an isolation bed to an ordinary bed to admit a non-COVID-19 patient is c _n + c _b − ∂h _t(x _t, y _t, w _t)/∂y _t − ∂h _t(x _t, y _t, w _t)/∂w _t. The marginal cost of subsidizing an elective patients from the waiting list is c _s − ∂h _t(x _t, y _t, w _t)/∂w _t. The cost difference of these two decisions is c _n + c _b − c _s − ∂h _t(x _t, y _t, w _t)/∂y _t, which is decreasing in y _t. Similarly, we define three curves in (y _t, w _t) plane to illustrate the optimization process. We use superscript ‘p’ to denote the marginal costs incurred in the post-peak phase.

$$\begin{array}{cc}& Y_t^p(w_t,x_t)=\sup \{y_t:c_n+c_b-\partial h_t(x_t,y_t,w_t)/\partial y_t-\partial h_t(x_t,y_t,w_t)/\partial w_t<0\},\\ & W_t(y_t,x_t)=\inf \{w_t:c_s-\partial h_t(x_t,y_t,w_t)/\partial w_t<0\},\\ & Z_t^p(w_t,x_t)=\sup \{y_t:c_n+c_b-c_s-\partial h_t(x_t,y_t,w_t)/\partial y_t<0\}.\end{array}$$

Here, $Y_t^o(w_t,x_t)$ is the largest y _t which satisfies the requirement that increasing isolation beds is cost effective in the outbreak phase; similarly, $Y_t^p(w_t,x_t)$ is the one in the post-peak phase. W _t(y _t, x _t) is the smallest w _t which satisfies the condition that reducing the length of waiting list is cost effective. $Z_t^o(w_t,x_t)$ is the largest y _t which satisfies the condition that reducing the waiting list is more cost effective than reserving isolation beds in the outbreak phase and $Z_t^p(w_t,x_t)$ is the largest y _t which satisfies the condition that reducing the waiting list is more cost effective than transferring isolation beds to ordinary beds.

Let $({\widehat{y}}_t,{\widehat{w}}_t)$ ($({\tilde{y}}_t,{\tilde{w}}_t)$, resp.) denote the minimizer of V _t corresponding to the smallest y _t and w _t in the outbreak phase (the post-peak phase, resp.). That is, at such a point (y _t, w _t), we have $Y_t^o(w_t,x_t)=W_t(y_t,x_t)=0$ ($Y_t^p(w_t,x_t)=W_t(y_t,x_t)=0$, resp.). As the pandemic progresses, the hospital manager can make dynamic adjustments to utilize the limited inpatient beds. For example, if the cost difference $Z_t^o(w_t,x_t)$ is negative, reserving more isolation beds to cope with COVID-19 patients is a cost effective strategy in the outbreak period. If the cost difference, $Z_t^p(w_t,x_t)$, is positive, transferring excessively reserved isolation beds into ordinary beds to admit non-COVID-19 patients is a cost effective strategy in the post-peak period. By characterizing the monotone property of these curves, a basic scheduling rule can be identified in the following proposition to assist the hospital manager in making patient admission and bed allocation decisions.

Proposition 5

In periodt, we have

• (i)Ash_t(x_t, y_t, w_t) is multimodular in (y _t, w _t) for x _t ⩾ 0, then $Y_t^o(w_t,x_t)$ , $Y_t^p(w_t,x_t)$ , $Z_t^o(w_t,x_t)$ , and $Z_t^p(w_t,x_t)$ are decreasing in the number of elective patients on the waiting list;
• (ii)if$w_t⩽{\widehat{w}}_t$,$Z_t^o(w_t,x_t)$is located to the left of$Y_t^o(w_t,x_t)$and aboveW_t(y_t, x_t); if$w_t<{\widehat{w}}_t$, the curve$Z_t^o(w_t,x_t)$is located underW_t(y_t, x_t) and to the right of$Y_t^o(y_t,x_t)$.
• (iii)if$w_t⩽{\tilde{w}}_t$,$Z_t^p(w_t,x_t)$is located to the left of$Y_t^p(w_t,x_t)$and aboveW_t(y_t, x_t); if$w_t<{\tilde{w}}_t$, the curve$Z_t^p(w_t,x_t)$is located underW_t(y_t, x_t) and to the right of$Y_t^p(y_t,x_t)$.

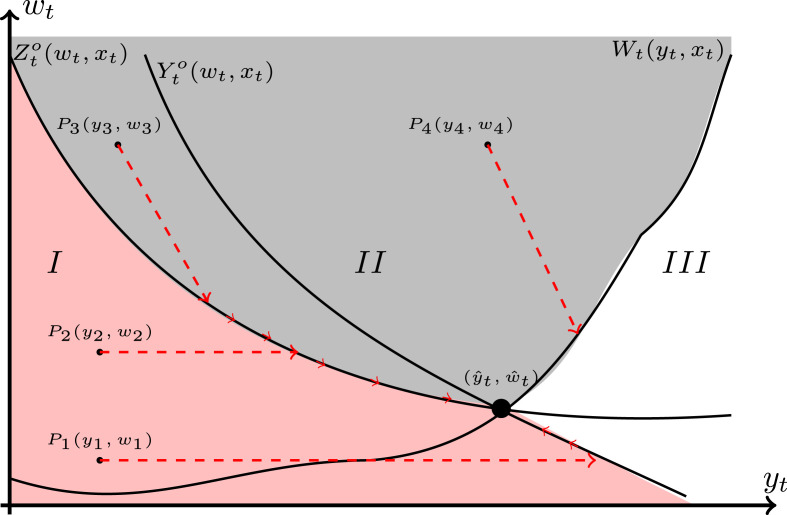
Proportion 5 reveals the monotone property of three curves in the (y _t, w _t) plane which is presented in Fig. 2 . Because both y _t and w _t are non-negative, these curves locate on the first quadrant of the (y _t, w _t) plane. In addition, the monotonicity properties of $Y_t^o(w_t,x_t)$ and $Z_t^o(w_t,x_t)$ are similar to the monotonicity properties of $Y_t^p(w_t,x_t)$ and $Z_t^p(w_t,x_t)$, respectively; thus, we only present the changes of marginal costs in the outbreak phase. In the post-peak phase, the curves of $Y_t^o(w_t,x_t)$ and $Z_t^o(w_t,x_t)$ in Fig. 2 can be replaced by $Y_t^p(w_t,x_t)$ and $Z_t^p(w_t,x_t)$, respectively, and similar insights hold.

Proposition 5(i) shows that, either in outbreak phase or post-peak phase, the number of reserved isolation beds for COVID-19 patients is sensitive to the number of elective patients on the waiting list. This might help explain why less urgent categories have to be canceled or postponed due to the COVID-19 pandemic. For example, in the UK, millions of operations had been postponed by NHS to tackle the COVID-19 crisis (The Guardian, 2020).

To illustrate Proposition 5(ii), we divide the first quadrant of the (y _t, w _t) plane into three regions. Region I is the area on the left side of both $Y_t^o(w_t,x_t)$ and $Z_t^o(w_t,x_t)$. Region II is located above $Z_t^o(w_t,x_t)$ and W _t(y _t, x _t). Region III is located to right side of W _t(y _t, x _t) and above $Y_t^o(w_t,x_t)$. For a state located in different regions, we have the following decision guidelines, which can help the hospital managers.

• ●In region I (colored with pink), it is optimal to primarily retrofit the ordinary beds with the negative pressure facilities as reserved isolation beds to cope with COVID-19 patients. For any point in this area, e.g., P ₁(y ₁, w ₁), we draw a horizontal line that intersects with $Y_t^o(w_t,x_t)$. The intersection point is denoted by $(Y_t^o(w_0,x_t),w_0)$. Because $w_0<\widehat{w}$, the hospital manager should retrofit $Y_t^o(w_0,x_t)-y_t$ ordinary beds into isolation beds. In addition, if $w_t⩾\widehat{w}$ (e.g., a point P ₂(y ₂, w ₂)), the hospital manager should first retrofit $\widehat{y}-Z^o(w_t,x_t)$ ordinary beds into isolation beds, and then subsidize Z ^o(w _t, x _t) − w _t elective patients and move them away from the waiting list.
• ●In region II (colored with gray), it is optimal to mainly subsidize elective patients and move them away from the waiting list. For any point in this area, e.g., P ₄(y ₄, w ₄), we draw a line segment with slope − 1 to intersect with W _t(w _t, x _t), and let $(y_t^0,W_t(y_t^0,x_t))$ be the intersection point. The hospital manager should only subsidize $W_t(y_t^0,x_t)-\widehat{w}$ elective patients. Similarly, for a point P ₃(y ₃, w ₃), we draw a line segment with slope − 1 to intersect with $Z_t^o(w_t,x_t)$, and let $(Z_t^o(w_t,x_t),w_t)$ be the intersection point. In such a scenario, the hospital manager should subsidize $w_t-\widehat{w}$ elective patients and retrofit $\widehat{y}-Z_t^o(w_t,x_t)$ ordinary beds as isolation beds.
• ●In region III (colored with white), the hospital manager can only subsidize more elective patients to reduce the length of waiting list. If any point in this area intersects with W _t(y _t, x _t), then $W_t(y_t^0,x_t)-\widehat{w}$ elective patients should be subsidized and moved away from the waiting list. In addition, it is note that the reserved isolation beds, y _t, is larger than that in other regions. Thus, if the hospital manager is facing a larger y _t, it implies that these reserved isolation beds are adequate to deal with the COVID-19 patients. Next, if the arrival of COVID-19 patients is continuously decreasing, the hospital manager needs to consider transferring isolation beds into ordinary beds in the post-peak phase.

In summary, applying Proportion 5 we conclude that the hospital manager should dynamically adjust the number of reserved isolation beds, especially in the outbreak and the post-peak phases. For example, the first wave of COVID-19 outbreak in HK, 66 babies, 5 cancer patients, and 15 pregnant women were referred to private hospitals (Cheung, 2020); in the mean time, facing such a serious situation, 400 isolation beds (‘second-tier’ beds) are offered in HK to accommodate the surging of confirmed COVID-19 cases. However, On 17th April 2020, according to the announcement from the Hospital Authority in HK, the utilization rate of ‘first-tier’ isolation beds dropped to around 50%, and there are 116 COVID-19 patients admitted using the ‘second-tier’ isolation beds (The Hospital The HK Hospital Authority, 2020). This implies that the isolation beds are not fully utilized. Therefore, it is necessary for the hospital manager to optimize the allocation of these excessively reserved isolation beds, rather than keeping a large number of empty beds.

Fig. 2.

The changes of marginal costs on w_t and y_t.

6. Numerical studies

In this section, we conduct numerical experiments to illustrate theoretical outcomes and to investigate the performance of the dynamic allocation rule. In reality, the COVID-19 situation varies in different countries and regions, which is corresponding to their actions about effective test, trace, isolate, and support systems (Han et al., 2020). High-level pandemic alert is implemented in response to a fast transmission of virus. While a low-level pandemic alert is to cope with the situation that the number of confirmed cases and transmission rate are low.

In numerical experiments, we classify the pandemic alerts of different countries and regions into three categories, namely weak, medium, and serious, to validate the effectiveness of dynamic allocation rule. We compare the expected operation cost between the static policy (i.e., keeping a fixed number of isolation beds) and our proposed dynamic allocation rule. We are particularly interested in the degree of cost saving of utilizing our dynamic allocation rule in comparing with the static policy and finding out the situation under which it works the best. We also investigate the effect of subsidy schemes by comparing experiment outcomes with and without subsidy schemes. The parameter settings are summarized in Table 1 .

Table 1.

Numerical settings.

Parameters	Value
Total number of decision periods T	16
Total number of inpatient beds K	120
The initial number of isolation beds y1	20
The initial number of elective patients on the waiting list w1	50
The arrival rate of COVID-19 patients εt	αc ∈ {1.4, 1.7, 2}, ut ∼ N(0, 2)
The arrival rate of elective patients δt	αn = 0.85, kt ∼ N(0, 2)
The arrival rate of emergency patients λt	Following a Poisson with mean 2
The number of COVID-19 patients being discharged from the system ${\xi }_t^c$	Uniformly distributed over [0.4, 0.5]
The number of non-COVID-19 patients being discharged from the system ${\xi }_t^n$	Uniformly distributed over [0.4, 0.5]
The unit idling cost of an isolation bed co	3
The unit cost of retrofitting an ordinary bed into an isolation bed cb	10
The unit cost for admitting a non-COVID-19 patient cn	1
The unit penalty cost if a COVID-19 patient is not timely admitted cp	500
The unit transferring cost of using an isolation bed to admit non-COVID-19 patients cd	2
The unit waiting cost cw	1
The financial subsidy $c_s(n_{3,t})=a_1{n}_{3,t}^2+a_2{n}_{3,t}$	(a1, a2) ∈ {(1, 19), (2, 18), (3, 17), (4, 16)}
The discount factor γ	0.9

Note: The normal distribution is referred to as N(μ, σ) with mean μ and variance σ.

We consider a fever clinic with a capacity of 120 inpatient beds in a public hospital. The clinic divides all inpatient beds into isolation and ordinary beds with initial numbers of 20 and 100, respectively. Demand for COVID-19 patients is measured by parameters α _c ∈ {1.4, 1.7, 2} and u _t ∼ N(0, 2) under three pandemic alters, including week, medium, and serious. Here, α _c is considered based on the reproductive number R ₀, which is ranged from 1.4 to 6.49 (WHO 2020b; Park et al., 2020). Demand for elective patients is measured by parameters α _n = 0.85 and k _t ∼ N(0, 2). The arrival of emergency patients follows Poisson with mean 2. We set the waiting cost c _w = 1. The unit retrofitting cost c _b, transferring cost c _d, idling cost of an isolation bed c _o are 10, 2, 3, respectively. Other cost parameters include c _p = 500 and c _n = 1. To investigate the effects of the subsidy scheme, we experiment with a quadric function, i.e., $c_s=a_1{n}_{3,t}^2+a_2{n}_{3,t}$, with four different settings, where (a ₁, a ₂) ∈ {(1, 19), (2, 18), (3, 17), (4, 16)}. In line with literature, see Liu et al. (2019), the daily discharge rate is uniformly distributed. In all experiments, we assume the discharge rate of inpatients is on the support [0.4, 0.5]. We simulate the dynamic allocation decisions and the total cost based on the dynamic rule over 16 periods, and the discount factor is γ = 0.9. In addition, we relax the total bed capacity and analyze the effects of waiting cost in Section 6.4 to conduct the robust analysis; we validate the performance and results of our proposed dynamic scheduling rule with a larger case (i.e., a larger bed capacity) as well. Two flow charts showcasing of the solution algorithm can be found in Appendix C.

6.1. Numerical outcomes of three examples

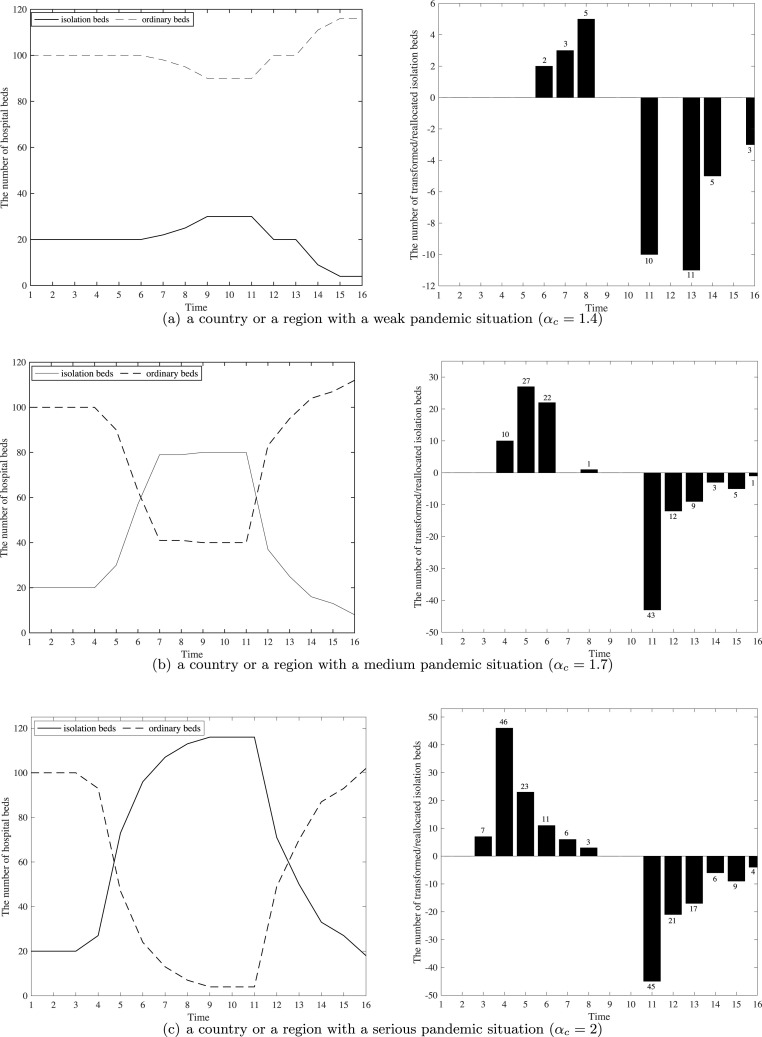
In this section, we use three examples to present the optimal outcomes based on our dynamic allocation rule. In general, when the reproduction number is greater than 1, local pandemics are growing; when the reproduction number is smaller than 1, the number of infections gradually declines (Lloyd-Smith et al., 2005; Diekmann and Heesterbeek, 2000). Thus, in line with literature, we consider three pandemic alerts: weak (α _c = 1.4), medium (α _c = 1.7), and serious (α _c = 2); we choose α _c = 0.8 to present the pandemic situation in the outbreak and post-peak phases. We focus on studying bed allocation decisions in these two phases. By simulating the allocation of isolation and ordinary beds, the results are depicted in Fig. 3 .

Fig. 3.

The hospital beds allocation at different phases of pandemic (K = 120).

As we can see from Fig. 3(a), when a region is facing a weak pandemic situation, holding a certain number of isolation beds to cope with the pandemic is necessary, especially in the outbreak phase. Specifically, Fig. 3(a) shows that total number of 10 ordinary beds are retrofitted into the isolation beds. However, after the peak phase, given the surging demand of elective patients and more vacated isolation beds, 29 isolation beds are transformed back into ordinary beds to admit the elective patients.

Fig. 3(b) shows allocation results when a region is facing a medium pandemic alert. In the first 4 periods, the initial reserved isolation beds can cope with those newly arrived COVID-19 patients. Thus, there is no significant change in terms of the number of two types of beds. However, with more confirmed COVID-19 cases arising in the following periods, more ordinary beds are retrofitted into isolation beds to admit those COVID-19 patients. Since period 11, the excessively reserved isolation beds are gradually transformed back into ordinary beds to admit non-COVID patients. Also, we note that the number of reserved isolation beds does not decline immediately after the peak phase. The reason is that, to avoid the potential risk of the second wave of the COVID-19 pandemic, it is necessary to ensure the adequate number of isolation beds within several time periods. In this case, 80 isolation beds are used to cope with the potential second wave of the COVID-19 pandemic.

Fig. 3(c) presents optimal bed allocation results when facing a serious pandemic alert. Compared to the medium case, this scenario shows a different trend, especially during the outbreak phase. As we can see from Fig. 3(c), there exists a sharp increase since the 4th period. This is because that the COVID-19 appears highly contagious in a short time. Therefore, the hospital manager must take immediate action, i.e., creating more isolation beds by retrofitting the ordinary beds, to deal with a surging number of COVID-19 patients. This experiment result shows that 96 ordinary beds are retrofitted as isolation beds. Similarly, a total of 116 isolation beds are reserved within three periods to avoid the potential risk of second wave. When facing a stabilized situation in the post-peak phase, the excessively reserved reservation beds are transformed back to admit the elective patients.

• (a)a country or a region with a weak pandemic situation (α _c = 1.4)
• (b)a country or a region with a medium pandemic situation (α _c = 1.7)
• (c)a country or a region with a serious pandemic situation (α _c = 2)

Table 2 presents the length of waiting list in each period under three pandemic alerts. If a region is facing a weak pandemic situation, the waiting list is quite short. It is because that a small number of isolation beds are needed to cope with the COVID-19 patients. Elective patients on the waiting list can be admitted. When a region is facing the medium/serious pandemic situation, the length of waiting list first decreases, due to the subsidy scheme and the decreasing number of arrivals from elective patients. In the following periods, the length increases again. The reason may be that the number of ordinary beds gets smaller, and fewer elective patients are admitted, which lengthens the waiting list. After some periods, the waiting list gets shorter. This can be caused by the increasing number of ordinary beds as shown in Fig. 3(b). In periods 14–16, the waiting list gets slightly longer, due to the increasing arrivals of elective patients in the post-peak phase.

Table 2.

The length of the waiting list in each time period (K = 120).

Time	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
αc = 1.4	50	35	26	21	16	4	0	0	0	0	4	0	0	0	0	0
αc = 1.7	50	37	21	6	0	2	10	13	18	28	51	20	12	8	18	28
αc = 2.0	50	34	14	0	5	7	11	16	20	34	62	33	21	14	24	33

6.2. Performance comparison with a static bed allocation policy

In this experiment, we consider a benchmark case with a fixed number of isolation beds over the whole planning periods and with subsidy scheme provided. We define a ratio $V_c^d/V_c^s$, where $V_c^s$ ($V_c^d$, resp.) is the expected cost incurred using the static policy (the dynamic scheduling rule, resp.). The numerical outcomes are summarized in Table 3 .

Table 3.

The cost ratio between the static policy and the dynamic scheduling rule (K = 120).

Fixed isolation beds	10	20	30	40	50	60	70	80	90	100	110	120
αc = 1.4	0.284	0.814	0.725	0.575	0.439	0.343	0.272	0.218	0.179	0.160	0.157	0.156
αc = 1.7	0.269	0.336	0.418	0.497	0.583	0.653	0.665	0.628	0.525	0.471	0.460	0.458
αc = 2.0	0.297	0.342	0.387	0.436	0.485	0.530	0.579	0.621	0.664	0.701	0.776	0.872

If we compare the cost ratio in each column, we can see that, among three cases, when facing a serious pandemic alert, our dynamic approach is slightly better than the static policy. The underlying reason is that, even though putting aside all the beds as isolation beds, total bed capacity cannot handle the surging number of COVID-19 patients. In such a serious situation, both static and dynamic policies need to reserve a large amount of isolation beds throughout the whole horizon. For a region facing a weak pandemic alert, reserving a small number of isolation beds is able to cope with the demand from the COVID-19 patients. The dynamic approach will not significantly reduce the total cost. While for a region facing a medium pandemic alert, the dynamic approach can effectively cope with the demand of COVID-19 patients and, at the same time, reduce idling costs of excessively reserved isolation beds. In this scenario, the dynamic approach can reduce the cost of the static policy by at least 33.5%.

In addition, for a region facing a serious pandemic alert, the dynamic scheduling rule is slightly better than the static policy. In such a serious situation, holding a large number of isolation beds is a reasonable manner to cope with COVID-19 patients. For example, the square-cabin hospitals are created in Wuhan, China to treat and quarantine a large number of patients with mild coronavirus infections. Similarly, in Hong Kong, temporary community isolation facilities have been established to receive mild COVID-19 patients. These isolation facilities can substantially reduce the need and pressure of public hospitals to admit COVID-19 patients as well. Following this way, reprioritization of non-COVID-19 patients can ensure that the public hospital could still provide essential care, especially for emergency and cancer patients.

When a region is facing a weak pandemic alert, reserving a fixed and smaller number of isolation beds is able to serve the COVID-19 patients. In contrast, if a region is facing a medium pandemic alert, the dynamic scheduling rule is a good option to avoid excessively reserved isolation beds. In terms of cost control, the analysis of hospital capacity using dynamic approach provides a significant reference point to the hospital managers, especially how the isolation and ordinary beds allocations can be efficiently coordinated.

6.3. Performance comparison of different subsidy schemes

In this section, we compare the experiment outcomes with and without subsidy schemes. The results are listed in Table 4 . For the subsidy scheme, we assume the subsidy amount offered for each patient is a linear function of the patient's position in the waiting list. For example, if the subsidy rule is s = 20 + 2(w _t − position), it means that each patient can get at least a subsidy amount of 20 units, and the patient at the head of the queue can obtain 2 more units than the following one. We then design four subsidy rules listed in Table 4: all have a fixed part of 20, and their linear slopes are 2, 4, 6, and 8, respectively. In all these subsidy schemes, the total subsidy amount the system needs to pay is an increasing convex function of the number of subsidized patients, which is in line with our original assumption.

Table 4.

The effects of the subsidy scheme (α_c = 2).

Evaluation criteria
Subsidy rule		Total cost		Average queue length
		Value	Δc	Value	Δq
Without Subsidy	–	120,108	–	67.9	–
Subsidy Rule 1	$c_s=n_{3,t}^2+19n_{3,t}$	36,897	0.31	11.3	0.17
Subsidy Rule 2	$c_s=2n_{3,t}^2+18n_{3,t}$	50,294	0.42	17.9	0.26
Subsidy Rule 3	$c_s=3n_{3,t}^2+17n_{3,t}$	62,987	0.52	23.6	0.35
Subsidy Rule 4	$c_s=4n_{3,t}^2+16n_{3,t}$	75,080	0.62	28.5	0.42

To measure the differences with and without subsidy, we use two ratios ${\mathrm{\Delta }}_c=V_c^s/V_c^n$ and Δ_q = L _s/L _n, where $V_c^s$ ($V_c^n$, resp.) is the total expected cost with a subsidy scheme (without a subsidy scheme, resp.), and L _s (L _n, resp.) is the average queue length with a subsidy scheme (without a subsidy scheme, resp.). As we can see from Table 4, subsidy scheme yields a lower total cost and a shorter queue length. By comparison of four subsidy schemes, the values of Δ_c and Δ_q are decreasing when a more generous amount of subsidy is offered to an elective patient. That is, because subsidy cost gets higher when transferring the same number of patients in the waiting list; the effect of subsidy scheme gets less significant.

Samiedaluie et al. (2017), the surging number of COVID-19 patients has created intense pressure on public hospital managers and governments. Meanwhile, elective patients are suffering the long waiting time from the over-congested healthcare systems. However, investment in new capacity for serving more elective patients during the COVID-19 pandemic is unrealistic. It is because this is an expensive investment and it is time-consuming as well. In contrast, the private system can provide additional medical faculties and services as they are unable to admit COVID-19 patients. Thus, our work investigates the effects of different subsidy schemes on mitigating the congestion in the public healthcare system and reducing waiting time for elective patients.

In such a complex environment, our numerical results show that offering subsidies can effectively reduce the total cost. That is, the subsidy scheme is valuable to elective patients, especially for those highly time-sensitive patients. It is because that they have joined the waiting list for a long time; receiving the subsidy and transferring to the private system can benefit them from avoiding wait too long. It is noteworthy, even offering a more generous amount of subsidy, the average queue length is significantly shorter with a subsidy scheme than without offering subsidy.

6.4. The robust analysis

In this section, we validate our dynamic scheduling rule in more complex scenarios. We first investigate the impacts of hospital bed capacity and the unit waiting cost on the total cost. This sensitivity analysis result can help managers to consider whether or not to expand capacity. Then, we populate a larger dataset to validate the performance of our proposed dynamic scheduling rule.

6.4.1. The effects of expansion capacity and waiting cost

Thus far, we note that while our current numerical experiments focus on the fixed bed capacity as 120 and unit waiting cost as 1. In this section, we consider a scenario in which the beds capacity is changing over time; we also investigate the impact of the waiting cost on the total cost. Thus, we change the bed capacity from 100 to 240 in increments of 20, and we vary unit waiting cost w from 2 to 16 in increments of 2. Other parameter settings are the same as those values in the base setting.

Following the previous experiments, Fig. 4 (a) presents the effect of hospital bed capacity on the cost ratio, i.e., $V_c^s/V_c^n$. The numerical result shows the subsidy scheme works best with a moderate size of bed capacity. In this example, it is 180 and the total cost reduced by 57% due to subsidy scheme. In a scenario with ample bed capacity, the subsidy scheme does not work that well because elective patients can be directly admitted into the system. Also, when bed capacity is scarce, relying on subsidy scheme is not enough as the waiting list is too long. In that situation, the manager may have to consider to solve the problem in another approach such as building mobile cabin hospitals. As we can see from Fig. 4(b), the expected cost first decreases and then increases in the unit waiting cost, while the average length of the waiting list is always decreasing.

Fig. 4.

The effects of bed capacity and waiting cost on the total cost.

6.4.2. Robustness testing

In our base setting, the numerical examples focus on somewhat the medium medical systems. The proposed dynamic scheduling rule can handle relatively the large systems as well. Thus, in this section, we consider a fever clinic with a larger capacity of 360 isolation beds in a public hospital. This setting is also reasonable and fits the facts. For example, there are 90 isolation beds (out of 1440 inpatient beds) in the Queen Mary Hospital, which is one of the public district general hospitals in Hong Kong to admit COVID-19 patients. The capacity setting (K = 360) in our work is also ten times as large as the base setting in Liu et al. (2019).

Given a larger capacity, Table 5 shows the cost ratio between the static policy and dynamic scheduling rule. Compared these results to the outcomes presented in Table 3, we can find that our dynamic scheduling rule is robust; this result implies that the proposed dynamic scheduling rule can handle relatively large systems as well. For a region facing a medium pandemic alert, our dynamic approach works efficiently to deal with the demand of COVID-19 patients by reducing the operational cost, especially through converting more ordinary beds and utilizing reserved isolation beds simultaneously. In such a scenario, the total cost can be reduced by at least 39.5%. For a region facing a weak pandemic alert, our dynamic approach can cut down at least 28.6% of the total cost compared with the static policy. For a region facing a serious alter, the challenging issue will be admitting patients as early as possible; then, reserving a large number of isolation beds becomes the most reasonable manner to handle the surging number of COVID-19 patients.

Table 5.

The cost ratio between the static policy and the dynamic scheduling rule (K = 360).

Fixed Isolation Beds	30	60	90	120	150	180	210	240	270	300	330	360
αc = 1.4	0.381	0.653	0.714	0.437	0.288	0.205	0.155	0.134	0.119	0.109	0.108	0.108
αc = 1.7	0.414	0.486	0.550	0.595	0.605	0.595	0.570	0.564	0.552	0.537	0.537	0.536
αc = 2.0	0.562	0.623	0.681	0.719	0.744	0.757	0.748	0.764	0.778	0.804	0867	0.935

When facing a larger capacity, our numerical results show that a lower total cost and a shorter queue length can be obtained by implementing the subsidy scheme and our dynamic approach simultaneously. For example, when choosing the subsidy rule 4 – (a ₁, a ₂) = (4, 16), two evaluation ratios Δ_c and Δ_q are 0.6 and 0.56, respectively, compared with the benchmark, i.e., without subsidy. Furthermore, we validate bed allocation decisions during the outbreak and post-peak phases of the COVID-19 pandemic. By simulating the allocation of isolation and ordinary beds, we find that the numerical results (K = 360) largely preserve the results obtained from our base setting. We present these numerical results in Appendix D.

7. Conclusion and implication

In this paper, we study the issue of hospital beds allocation and waiting list management to serve three classes of patients: COVID-19, emergency and elective patients. Our work is motivated by problems in capacity planning given a number of pandemics in the 21st century, especially the most recent COVID-19 pandemic. We consider the two-way bed allocation decisions on the supply side and managing the waiting list of elective patients on the demand side. In the outbreak phase, facing the surging number of COVID-19 patients, the manager can consider to retrofit ordinary beds into isolation beds with negative pressure facilities; in the post-peak phase, the manager can transfer some excessively reserved isolation beds back into ordinary beds. The extensive numerical examples are conducted to gain insights on managing the system.

7.1. Conclusionconclusion

We demonstrate the multimodularity of the total expected cost function on the number of reservation beds and the length of waiting list. We show that a longer waiting list makes it harder to reserve more isolation beds. Hence it is better to use subsidy scheme to shorten the waiting list. By characterizing the marginal costs of key decisions in our model, we also graphically demonstrate the optimal decisions on bed allocation and patient subsidy, facing different combinations of the number of reserved isolation beds and waiting list.

We conduct some numerical experiments to compare the effects of our dynamic allocation policy with that of a static policy (namely, a policy with a fixed number of isolation beds). We find that our dynamic allocation policy works best when facing a medium-alert pandemic situation and it can reduce the total cost by at least 33.5%. In a serious-alert situation, beds are all reserved for COVID-19 patients and hence there is little room left for dynamic adjustment of bed capacities. In a weak-alert situation, demand for isolation bed is small and hence dynamic allocation also does not work well.

Through our numerical studies, we find that a subsidy scheme can greatly reduce the total cost and shorten the waiting list of elective patients, in comparing with the scenario without subsidy. Our numerical study shows that, with subsidy, the total cost can be reduced by 38% and the waiting list of elective patients can be reduced by 58% compared to the outcome without a subsidy scheme. We also find that the subsidy scheme works best when facing moderate bed capacity.

7.2. Managerial insights

In this work, we provide a contemporary study of healthcare operations to cope with COVID-19 pandemic. The emergence of COVID-19 has forced public hospitals to reorient their routine for dealing with multiple types of patients: COVID-19 and non-COVID-19 patients (i.e., elective and emergency), where COVID-19 patients should be treated in a negative pressure environment avoiding secondary infections. Thus, our work aims to improve the ability of hospital administrators responding effectively to bed capacity allocation and patients admission decisions, especially trough bed transformation and subsidy schemes.

The healthcare organizations are facing significant challenges in different phases of COVID-19 pandemic, especially outbreak and post-peak phases. For example, due to the existing of COVID-19 patients, capacity planning has to consider infections among patients and hospital beds have to be separated into two types: ordinary and isolation beds. For the public hospital administrators, our proposed model can assist them in making appropriate decisions about how many isolation beds should be reserved to cope with COVID-19 patients. When deciding how to allocate limited inpatient beds, hospital administrators must make the best use of isolation beds and ordinary beds in different phases of COVID-19 pandemic, especially retrofitting more ordinary beds with the negative pressure facilities as isolation beds when facing the surging number of COVID-19 infections. To relieve the congested public system, our dynamic scheduling rule can assist hospital administrators in subsidizing a certain number of elective patients and move them away from the waiting list. Numerical example results show that the average length of the waiting list is decreasing when hospital administrators implement our proposed dynamic allocation with a subsidize rule. By implementing proposed bed transformation and subsidy schemes, hospital administrators can effectively coordinate hospital resources; this not only can reduce the pressure of public hospitals, but also ensure that the public hospital could still provide essential care, especially for emergency and cancer patients.

7.3. Limitations

Our work presents a stepping stone to further study questions associated with dynamic medical resource allocation facing the COVID-19 pandemic. Some limitations could be studied in future research. First, it would be interesting to use real data to identify the time-dependent arrival rates of COVID-19 and elective patients in different phases of pandemic, e.g., predicting admission using triage information (Araz et al., 2019). Second, our work only focuses on the issue of internal bed allocation and coordination for a public hospital. Another research question is to study the coordination issues between public and private hospitals in the pandemic. Third, our work mainly investigate the allocation of inpatients beds to cope with COVID-19 patients under a mild condition; it is also worthwhile to explore the management of ICU beds to deal with those COVID-19 patients under a serious condition. Fourth, future research may investigate how triage of patients affects the medical resources allocation for different functional departments in a public hospital.

Appendix A. Supplementary data

The following is the Supplementary data to this article: