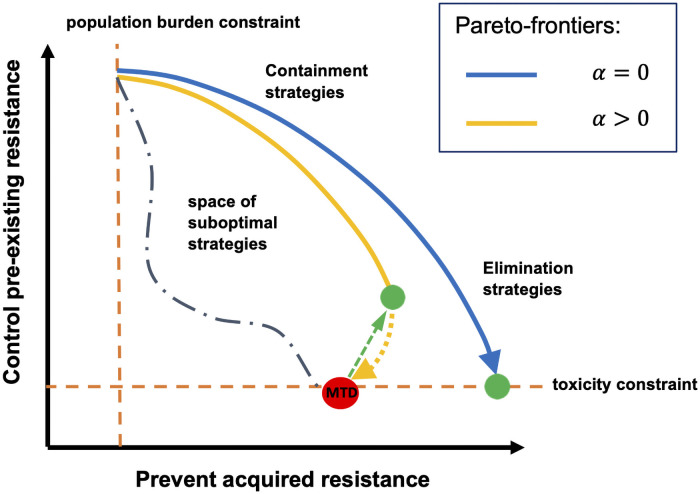
Fig 5. Trade-offs in treatment optimisation.

Every treatment strategy is necessarily a trade-off between preventing acquired resistance, by decreasing the population size, and suppressing pre-existing resistance, by allowing intercellular competition. The rate at which the population size can be decreased is constrained from above by the toxicity constraint as well as by finiteness of control leverage and, on the other hand, from below by the population burden constraint, which forces to apply control to stabilize the population size at some acceptable level. When no drug-induced effects are present (α = 0), the optimal treatment strategy is found somewhere on the blue Pareto-frontier; the arrow points to the direction where the cumulative drug concentration increases and the optimal elimination strategy (the green point) is given by the MTD-strategy. However, if drug-induced effects are present (α > 0), the optimisation must be done on a completely different, yellow Pareto-frontier, which exhibits a bifurcation point after which increasing the cumulative drug concentration becomes detrimental with both respects. In these cases, the optimal elimination strategy (the green point) is reached at intermediate dosages at the bifurcation point, which can be identified using the methods presented here. Hence, substantial Pareto-improvements (represented by the green arrow) may be achieved by switching from the MTD-strategy to the optimised treatments.