Test-trace-and-isolate and moderate contact restrictions offer sustainable exit strategies complementary to vaccination.
Abstract
The traditional long-term solutions for epidemic control involve eradication or population immunity. Here, we analytically derive the existence of a third viable solution: a stable equilibrium at low case numbers, where test-trace-and-isolate policies partially compensate for local spreading events and only moderate restrictions remain necessary. In this equilibrium, daily cases stabilize around ten or fewer new infections per million people. However, stability is endangered if restrictions are relaxed or case numbers grow too high. The latter destabilization marks a tipping point beyond which the spread self-accelerates. We show that a lockdown can reestablish control and that recurring lockdowns are not necessary given sustained, moderate contact reduction. We illustrate how this strategy profits from vaccination and helps mitigate variants of concern. This strategy reduces cumulative cases (and fatalities) four times more than strategies that only avoid hospital collapse. In the long term, immunization, large-scale testing, and international coordination will further facilitate control.
INTRODUCTION
As severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) is becoming endemic and knowledge about its spreading is accumulated, it becomes clear that neither global eradication nor population immunity will be achieved soon. Eradication is hindered by the worldwide prevalence and by asymptomatic spreading. Reaching population immunity without an effective vaccine or medication would take several years and cost countless deaths, especially among the elderly (1, 2). Moreover, evidence for long-term effects (“long COVID”) is surfacing (3–6), advising against strategies aiming to progressively exposing people to the disease so that they acquire natural immunity. Hence, we need long-term, sustainable strategies to contain the spread of SARS-CoV-2. The common goal, especially in countries with an aging population, should be to minimize the number of infections and, thereby, allow reliable planning for individuals and the economy, while not constraining individuals’ number of contacts too much (7). Intuitively, a regime with low case numbers not only would benefit public health and psychological well-being but also would profit the economy (8, 9).
However, control of SARS-CoV-2 is challenging. Many infections originate from asymptomatic or presymptomatic cases (10) or indirectly through aerosols (11), rendering mitigation measures difficult. Within test-trace-and-isolate (TTI) strategies, the contribution of purely symptom-driven testing is limited, but together with contact tracing, it can uncover asymptomatic chains of infections. The rising availability of effective vaccines against SARS-CoV-2 promises to relieve the social burden caused by nonpharmaceutical interventions (NPIs). However, it is unclear how fast the restrictions can be lifted without risking another wave (12–14) and how well vaccines will protect against more contagious or immune response–escaping variants. Additional challenges are the potential influx of SARS-CoV-2 infections (brought in by travelers or commuting workers from abroad), imperfect quarantine, limited compliance, and TTI and case-reporting delays. Last, any country’s capacity to perform TTI is limited, so spreading dynamics change depending on the level of case numbers. Understanding these dynamics is crucial for informed policy decisions.
RESULTS
Analytical framework: Overview
We analytically show the existence of a stable regime at low case numbers, where control of SARS-CoV-2 is much easier to achieve and sustain. In addition, we investigate mitigation strategies and long-term control for corona virus disease 2019 (COVID-19), where we build on our past work to understand the effectiveness of NPIs, particularly TTI strategies (15–17). The strategy that we propose does not rely on the availability of a cure or vaccine, and it is applicable not only to further waves of COVID-19 but also to other emerging diseases with pandemic potential. Nonetheless, we also show how vaccination campaigns will further facilitate the success of the proposed strategy, assuming a vaccination rate as planned for countries in the European Union (13).
For quantitative assessments, we adapt a susceptible-exposed-infectious-recovered (SEIR)–type compartmental model (18) to explicitly include a realistic TTI system that considers the challenges above. In our framework, individuals can be tested (and subsequently quarantined if tested positive) by three different mechanisms. First, symptomatic infections with COVID-19–specific symptoms would self-report or be diligently identified by surveillance and get a preferential test. Second, random asymptomatic screening would be homogeneously deployed in the general population disregarding symptoms so that every individual could be tested alike. Third, all the close contacts of those individuals recently tested positive by the two mechanisms mentioned above would also be tested. Understandably, limited resources pose a complex challenge for resource allocation, where efficient TTI would only be possible at low case numbers. We also built an interactive platform where enthusiastic readers can simulate scenarios different from those presented herein http://covid19-metastability.ds.mpg.de/.
A central parameter for our analysis is the level of contagious contacts kt (relative to pre–COVID-19). More precisely, kt refers to the fraction of infection risk–bearing encounters compared to pre–COVID-19 contact levels. We can then interpret kt in terms of the hidden reproduction number , which accounts for the number of offspring infections generated by individuals unaware of being infectious, i.e., hidden infections in a naive and fully susceptible population (15). Thus, in terms of , kt can be understood as the ratio between the offspring infections a hidden individual would generate in the presence and in the absence of NPIs, in other words, . Apart from direct contact reduction, contributions that allow increasing kt without compromising the stability of the system also come from improved hygiene, mandatory face mask policies, frequent ventilation of closed spaces, and avoiding indoor gatherings, among other precautionary measures. As the latter measures are relatively fixed, direct contact reduction remains the central free variable, which is also the one tuned during lockdowns. All other parameters (and their references) are listed in Table 1.
Table 1. Model parameters.
| Parameter | Meaning | Value (default) | Range | Units | Source |
| M | Population size | 1,000,000 | People | – | |
| R 0 | Basic reproduction number | 3.3 | 2.2–4.4 | – | (19, 20) |
| 𝜈 | Registered contacts (quarantined) | 0.075 | – | Assumed | |
| 𝜖 | Lost contacts (quarantined) | 0.05 | – | Assumed | |
| 𝛾 | Recovery/removal rate | 0.10 | 0.08–0.12 | Day−1 | (64, 65) |
| 𝜉 | Asymptomatic ratio | 0.32 | 0.15–0.43 | – | (51, 52, 54) |
| 𝜆s | Symptom-driven testing rate | 0.25 | 0–1 | Day−1 | Assumed |
| Symptom-driven testing rate (reduced capacity) | 0.1 | Day−1 | Assumed | ||
| 𝜆r | Random testing rate | 0.0 | 0.0–0.1 | Day−1 | Assumed |
| 𝜂 | Tracing efficiency | 0.66 | – | Assumed | |
| 𝜏 | Contact tracing delay | 2 | Days | Assumed | |
| Maximal tracing capacity | 50 | 10–75 | Cases day−1 | Assumed | |
| Φt | External influx | 1 | Cases day−1 | Assumed | |
| 𝜌 | Exposed-to-infectious rate | 0.25 | Day−1 | (10, 66) | |
| D L | Lockdown duration | 4 | 0–8 | Weeks | (27) |
| D ramp | Phase-transition duration (lockdown) | 1 | Weeks | (27) | |
| 𝜒τ | Fraction of contacts traced before becoming infectious |
0.61 | – | Eq. 17 | |
| 𝜒s,r | Fraction of contacts traced after becoming infectious, before being tested (symptomatic and random) |
0.30 | – | Eq. 20 | |
| 𝜒r | Fraction of contacts traced after becoming infectious, before being tested (random) |
0.39 | – | Eq. 18 |
Equilibrium at low case numbers
We find a regime where the spread reaches an equilibrium at low daily case numbers between the scenarios of eradication of the disease or uncontrolled spreading. The main control parameter that determines whether the system can reach an equilibrium is the level of contagious contacts kt.
If the reduction in the contact level kt is mild, then case numbers grow exponentially, as measures could not counterbalance the basic reproduction number [R0 ≈ 3.3 for SARS-CoV-2 (19, 20)] (Fig. 1B). In contrast, if the reduction in kt is strong and (together with hygiene and TTI) outweighs the drive by the basic reproduction number, then case numbers decrease to a low equilibrium value (Fig. 1D).
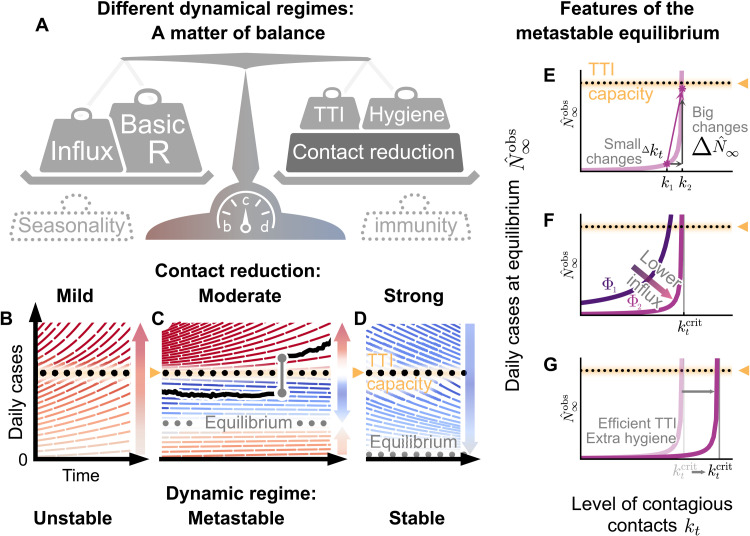
Fig. 1. Spreading dynamics depend on the balance between destabilizing and stabilizing contributions and on the level of case numbers.
(A) Among the factors that destabilize the spread, we find the basic reproduction number R0 and the external influx of infections (and, possibly, seasonality). On the other hand, increased hygiene, TTI strategies, contact reduction, and immunity contribute to stability. We specifically investigated how reductions in the contact level kt and limited TTI capacity determine the stabilization of case numbers. (B) At mild contact reduction (kt = 80% compared to pre–COVID-19 times), TTI is not sufficient; case numbers would grow even when TTI capacity is available. (C) At moderate contact reduction (kt = 60%), a metastable equilibrium emerges (gray dots) to which case numbers converge, if they were below the TTI capacity. However, destabilizing events (e.g., a sudden influx of infections) can push a previously stable system above the TTI capacity and lead to an uncontrolled spread (black line as an example). (D) Assuming strong contact reduction (kt = 40%), case numbers decrease even if the TTI capacity is exceeded. (E) Near to the critical level of contacts , small changes in the contact level will lead to a considerable increase in observed cases in equilibrium . (F) Reducing the influx of infections Φt (by closing borders or deploying extensive testing at arrival) reduces the number of infections. (G) Increasing the efficiency of manual contact tracing and additional measures such as increased hygiene and compulsory use of face masks will increase the maximum allowed level of contacts .
If the reduction in kt is moderate (and just about balances the drive by the basic reproduction number), we find a metastable regime: The spread is stabilized if and only if the overall case numbers are sufficiently low to enable fast and efficient TTI (Fig. 1C). However, this control is lost if the limited TTI capacity is overwhelmed. Beyond that tipping point, the number of cases starts to grow exponentially as increasingly more infectious individuals remain undetected (15).
The capacity of TTI determines the minimal required contact reduction for controlling case numbers around an equilibrium. If case numbers are sufficiently below the TTI capacity limit, then the maximum allowed level of contacts to enable the (meta-)stable regime in our default scenario (cf. Table 1, with R0 = 3.3) is [95% confidence interval (CI): [47, 76]]. When the level of contacts kt is below the threshold, case numbers asymptotically approach to an equilibrium that shows the following features: (i) When the level of contacts kt is close to its critical value , small changes in kt generate large modifications of the equilibrium level (Fig. 1E). (ii) Larger influxes lead to larger equilibrium values, however not modifying the maximum allowed level of contacts (Fig. 1F). (iii) Behavioral changes and policies leading to a reduction in the transmission probability will also lower the equilibrium value because the maximum allowed level of contacts would be larger (Fig. 1G). However, if case numbers exceed the TTI capacity limit, then a considerably stronger reduction in contacts is required to reach the stable regime, so that (95% CI: [38, 47]) (Fig. 2B, fig. S2B, and table S1).
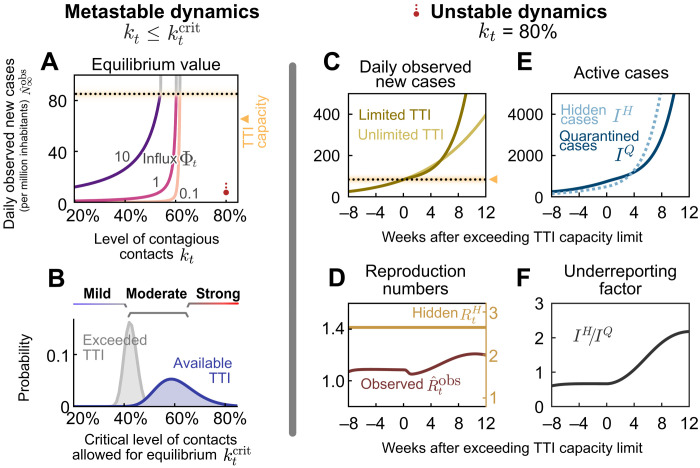
Fig. 2. When the TTI capacity is fixed, the contact level determines the dynamical regime.
(A and B) In the stable and metastable regimes, daily new cases approach an equilibrium value that depends on contact level kt and the external influx of new cases Φt. (A) The equilibrium value increases with increased contact level kt or higher influx Φt. No equilibrium is reached if either kt or Φt is above the respective (critical) threshold values. (B) The critical value represents the maximal contact level that is allowed to reach equilibrium and stabilize case numbers. If case numbers are below the TTI capacity limit, then higher values of are permitted for stabilization (blue) than if cases exceed TTI (gray). CIs originate from error propagation of the uncertainty of the underlying model parameters. (C to F) In the unstable dynamic regime (kt = 80%), a tipping point is visible when exceeding TTI capacity. We observe a self-accelerating increase of case numbers after crossing the TTI limit (C) and a subsequent increase of the reproduction number (D). Furthermore, the absolute number (E) and the fraction (F) of cases that remain unnoticed increase over time.
Equilibrium depends on influx and contact reduction
If an equilibrium is reached, the precise value of daily new cases at which the system stabilizes depends on both the contact level (kt) and the external influx of new cases (Φt) (Fig. 2A). In general, for realistic low values of influx Φt, the equilibrium level is low. However, increases steeply (diverges) when the contact level kt approaches the tipping point to unstable dynamics (Fig. 2, A and B). Such a divergence near a critical point is a general feature of continuous transitions between stable and unstable dynamics (21, 22). As a rule of thumb, in an analytical mean-field approximation (22), would be proportional to Φt and diverge when kt approaches its critical value from below
| (1) |
Robust control of the pandemic requires maintaining a sufficient safety margin from the tipping point (and the subsequent transition to instability) for two reasons. First, small fluctuations in kt and Φt (or other model variables) could easily destabilize the system. Second, near the critical value , reductions in kt are especially effective: Already, small further reductions below lead to substantially lower stable case numbers (Fig. 2A). Already, with moderate reductions in kt (50 % < kt < 60%), the spread can be stabilized to a regime of case numbers clearly below 10 per million (fig. S1B, lower right region).
Limited TTI and self-acceleration
If mitigation measures are insufficient, then case numbers rise and eventually surpass the TTI capacity limit. Beyond it, health authorities cannot efficiently trace contacts and uncover infection chains. Thus, the control of the spread becomes more difficult. We start our scenario with a slight increase in the case numbers over a few months, as seen in many European countries throughout summer 2020 (figs. S4 and S5). A tipping point is then visible in the following observables (Fig. 2, C to F)
First, when case numbers surpass the TTI capacity, the increase in daily new observed cases becomes steeper, growing even faster than the previous exponential growth (Fig. 2C, full versus faint line). The spread self-accelerates because increasingly more contacts are missed, which, in turn, infect more people. In this scenario, the accelerated spread arises solely because of exceeding the TTI limit, without any underlying behavior change among the population.
Second, after case numbers surpass the TTI limit, the observed reproduction number , which had been only slightly above the critical value of unity, increases substantially by about 20% (Fig. 2D). This reflects a gradual loss of control over the spread and explains the faster-than-exponential growth of case numbers. The initial dip in is a side effect of the limited testing: As increasingly many cases are missed, the observed reproduction number reduces transiently.
Third, compared to the infectious individuals who are quarantined IQ, the number of infectious individuals who are hidden IH (i.e., those who are not isolated or in quarantine) increases disproportionately (Fig. 2E), which is measured by the “underreporting factor” (IH/IQ) (Fig. 2F). The hidden infectious individuals are the silent drivers of the spread, as they, unaware of being infectious, inadvertently transmit the virus. This implies a considerable risk, especially for vulnerable people. The TTI system can compensate for the hidden spread at low case numbers because it uncovers hidden cases through contact tracing. However, at high case numbers, the TTI becomes inefficient: If the TTI measures are “slower than the viral spread,” many contacts cannot be quarantined before they become spreaders.
Reestablishing control with lockdowns
Once the number of new infections has overwhelmed the TTI system, reestablishing control can be challenging. A recent suggestion is the application of a circuit breaker (23–25), a short lockdown to substantially lower the number of daily new infections. Already, during the so-called first wave of COVID-19 in Europe (i.e., the time frame between March and June 2020), lockdowns have proven capable of lowering case numbers by a factor of 2 or more every week (corresponding to an observed reproduction number of ) (17, 26). With the knowledge that we now have acquired about the spreading of SARS-CoV-2, more targeted restrictions may yield a similarly strong effect.
Inspired by the lockdowns installed in many countries (27), we assume a default lockdown of 4 weeks, starting 4 weeks after case numbers exceed the TTI capacity limit, and a strong reduction of contagious contacts during a lockdown, leading to kt = 25% (which corresponds to an ; see table S2). We further assume that during lockdown, the external influx of infections Φt is reduced by a factor of 10 and that after the lockdown, a moderate contact reduction (allowing knLD = 60%) is maintained. By varying the parameters of this default lockdown, we show in the following that the lockdown strength, duration, and starting time determine whether the lockdown succeeds or fails to reach equilibrium.
In our scenario, a lockdown duration of 4 weeks is sufficient to reach the stable regime (Fig. 3A). However, if lifted too early (before completing 4 weeks), case numbers will rise again shortly afterward. The shorter an insufficient lockdown, the faster case numbers will rise again. In addition, it is advantageous to remain in lockdown for a short time even after case numbers have fallen below the TTI limit, to establish a safety margin, as shown above. Overall, the major challenge is not to ease the lockdown too early; otherwise, the earlier success is soon squandered.
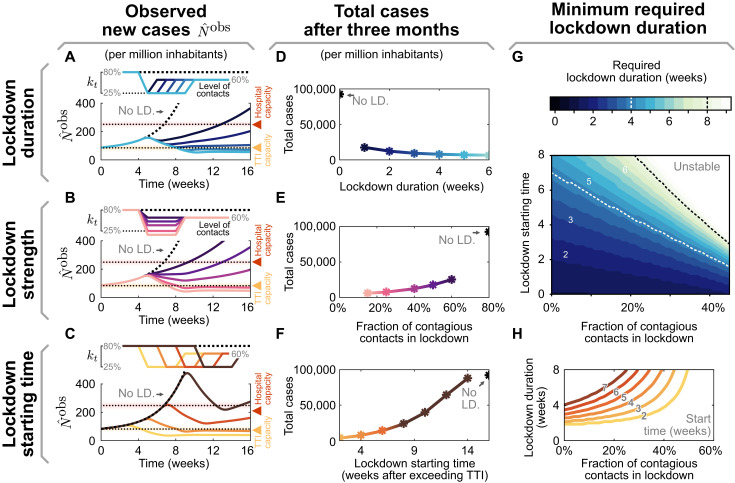
Fig. 3. The effectiveness of a lockdown depends on three primary parameters: its duration, stringency (strength), and starting time.
(A to C) Observed daily new cases for a lockdown (LD.), enacted after exceeding the TTI capacity. Reference parameters are a lockdown duration of 4 weeks, reducing contact level to kt = 25%, and a start time at 4 weeks after exceeding TTI capacity. We vary lockdown duration from 1 to 5 weeks (A), lockdown strength (B), and lockdown starting time (C) to investigate whether stable case numbers can be reached. (D to F) Total cases after 3 months, if the lockdown is parameterized as described in (A) to (C), respectively. (G and H) The minimal required duration of lockdown to reach equilibrium depends both on strength and start time. (G) Heavy contact reduction (leading to lower values of kt) and timely lockdown enacting can create effective short lockdowns (≤2 weeks, lower left, dark region). Whereas with mild contact reduction and very late start times, lockdowns become ineffective even when they last indefinitely (upper right, bright area). (H) Horizontal slices through the color map (G). Here, colors match (C) and (F) and correspond to the lockdown start time.
During a lockdown, it is necessary to severely reduce contagious contacts to decrease case numbers below the TTI capacity limit (Fig. 3B). In our scenario, the contact level has to be reduced to at least kLD = 25% to bring the system back to equilibrium. Otherwise, a lockdown that is slightly weaker would fail to reverse the increasing trend in cases. Furthermore, increasing the lockdown strength decreases both the required lockdown duration (Fig. 3, G and H) and the total number of cases accumulated over 3 months (Fig. 3E). This shows that stricter lockdowns imply shorter-lasting social and economic restrictions.
The earlier a lockdown begins after exceeding the TTI capacity limit, the faster control can be reestablished, and constraints can be loosened again (Fig. 3C). If started right after crossing the threshold, in principle, then only a few days of lockdown are necessary to bring back case numbers below the TTI capacity limit. On the other hand, if the lockdown is started weeks later, then its duration needs to increase (Fig. 3, C and D) and the total number of cases will be substantially larger (Fig. 3F). The parameter regime between these two options is relatively narrow; it is not likely that equilibrium can eventually be reached as a lockdown exceeds many weeks (cf. Fig. 3H). For practical policies, this means that if a lockdown does not start to show apparent effects after 2 or 3 weeks, then the strategy should be revised (this assessment time is necessary because of the delay of 1 to 2 weeks between contagion and case report).
Maintaining control without lockdowns
We show that repeated lockdowns are not required to maintain control over the COVID-19 spread if moderate contact reduction is maintained once case numbers are below the TTI capacity limit (an initial lockdown might still be necessary to establish control). A natural goal would be to keep case numbers below the hospital capacity. However, our model suggests that lowering them below TTI capacity requires fewer contact restrictions (in the long term), involves a shorter total lockdown duration, and costs fewer lives. In the following, we compare the long-term perspective of these two goals and their dependence on the necessary contact reduction.
In our scenario (Fig. 4), we start from the unstable regime, where the initial contact level (kt = 80% of the pre-COVID-19 level) is not sufficient to control the spread. We start a 2-week lockdown when crossing either the TTI or the hospital capacity. During the lockdown, contacts are reduced to kt = 25%. After the first and all subsequent lockdowns, contacts kt are reduced to 80, 60, or 40% relative to pre–COVID-19 levels, thus representing a mild, moderate, or strong reduction. When assuming mild contact reduction after lockdowns, case numbers rise after lifting the lockdown, independent of the chosen threshold (TTI or hospital capacity; Fig. 4A). Thus, repeated lockdowns are necessary.
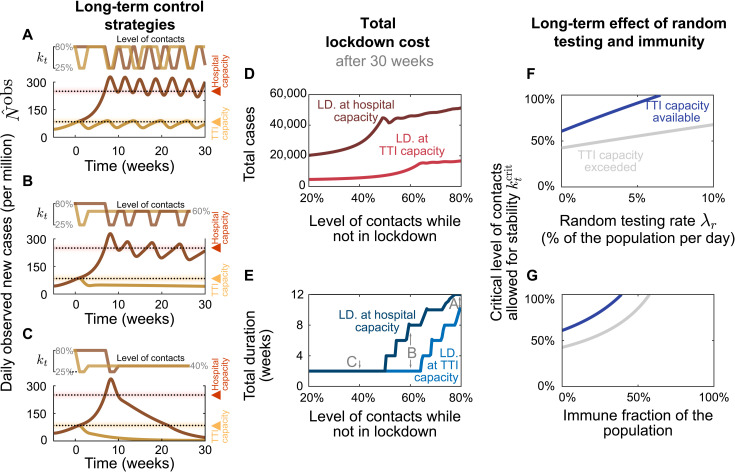
Fig. 4. From a long-term perspective, recurrent lockdowns are not required if the subsequent contact levels kt are sufficiently low to reach equilibrium.
A 2-week lockdown of default strength (reducing contact level to kt = 25% relative to pre-COVID-19 levels) is either enacted when the TTI (yellow lines) or the hospital (red lines) capacity limits are crossed. (A) Given only a mild contact reduction while not in lockdown (to kt = 80%), the imposed lockdowns need to reoccur with a high frequency. Moreover, the frequency at which they reoccur is higher at high case numbers (aiming at hospital capacity) than when aiming at the TTI capacity limit because of the self-accelerating effect described previously. (B) If the contact reduction remains moderate (to kt = 60%), lockdowns only need to reoccur if they fail to bring case numbers below TTI capacity. (C) Only lasting strong contact reduction (to kt = 40%) is sufficient to continue to bring down case numbers after the lockdown. (D and E) The total cost (in terms of cumulative cases and total lockdown duration) depends on the level of contact reduction and the lockdown policy: The cost is low if lockdowns are initiated at the TTI capacity limit and if the contact level kt after the lockdown is low. (F and G) Large-scale random testing (F) or immunization of the population [either after infection or through vaccination (G)] increases the maximal contact level allowed for stability .
However, maintaining a moderate contact reduction while not in lockdown (i.e., a contact level of kt = 60%) is sufficient to stay within the metastable regime, if lockdowns are enacted such that case numbers remain below the TTI capacity (Fig. 4B, yellow line). This is a promising perspective for a long-term control strategy that avoids recurrent lockdowns. Otherwise, if case numbers are above TTI capacity limit but below hospital capacity, then control of the pandemic requires repeated lockdowns (Fig. 4B, red line). Alternatively, lasting strong contact reductions even after the lockdown can be sufficient to drive down case numbers (Fig. 4C).
The advantage of the strategy to stay below the TTI capacity limit becomes very clear when considering the total cost of the required lockdowns: Independent of the degree of contact reduction, (i) the total number of cases (and consequently deaths and long COVID risk) is lower (Fig. 4D), (ii) the total duration spent in lockdown is shorter (Fig. 4E), and (iii) the frequency at which lockdowns have to reoccur—should the after-lockdown contact reduction not be enough to grant metastability—is lower (Fig. 4A). As case numbers and lockdown duration indicate economic costs, a strategy that respects the TTI limit offers a low economic toll, enables mid-term planning, and provides trust to people and society.
The scalability of random testing (screening) (28–30) and immunization programs play a critical role in long-term strategies; both will increase the maximum level of contacts allowed () to maintain control (Fig. 4, F and G). Early effects of immunity can be seen in our scenario of the system stabilized at hospital capacity: The need for lockdowns becomes less frequent over time (Fig. 4, A and B, red lines). However, acquiring natural immunity comes at the cost of a prolonged high level of case numbers, subsequent long COVID cases (4–6), and deceased people. Whereas the duration of the immunity is yet unknown (31), this phenomenon still shows that immunity effects play an increasing role as model predictions extend further into the future.
Vaccination greatly facilitates containment in the effective TTI regime
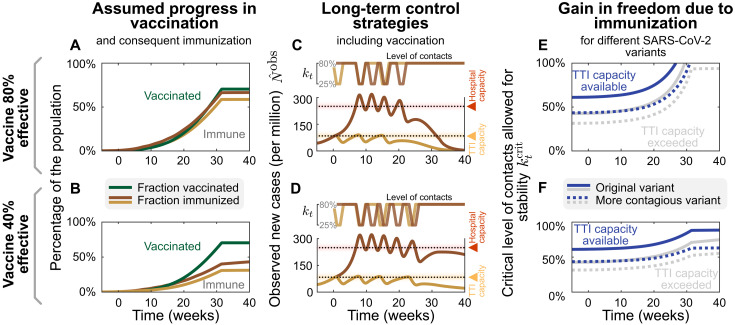
In the following, we show how growing immunity granted by vaccination programs further facilitates both reaching low case numbers below TTI capacity and the stable control thereof. For quantitative assessments, we studied the effect of COVID-19 vaccination programs and how they affect the two control strategies discussed in the previous section.
Investigating explicit vaccination scenarios, we assume that 80% of people getting offered vaccination accept this offer. Since, as of now, none of the available vaccines has been approved for people younger than 16 years, this corresponds to a vaccine uptake of roughly 70% of the overall population (for European demographics). We model the delivery and administration of all doses to be completed within 32 weeks (13), which is comparable to the increasing vaccination rate in the European Union. We investigate two scenarios: that the average vaccine efficacy against transmission is 80%, in line with reported values for current vaccines against the wild type and the widely dominant B.1.1.7 variant (32–34), or 40%, a possible scenario for partially immune-escaping variants.
Comparing the two different control strategies introduced in the preceding section, i.e., either aiming to keep case numbers below the TTI or below the hospital capacity limit, the progressing vaccination Fig. 5, A and B) will eventually lead to declining case numbers Fig. 5, C and D). However, this point will be reached several weeks earlier if case numbers are kept below TTI capacity. Until then, repeated lockdowns will remain necessary if contact reductions outside of lockdown are insufficient (see discussion in the preceding section). A decreasing number of infections will even be reached months earlier if TTI capacity is available than if it is overwhelmed.
Fig. 5. Growing immunity due to mass vaccination will lead to declining case numbers and enable increasing contact levels for 80% (top row) and 40% (bottom row) vaccine efficacy against transmission; we explore the effect of mass vaccination.
(A and B) Vaccine rollout is assumed to accelerate over 32 weeks, ending when 70% of the population have been vaccinated. (C and D) As in Fig. 4A, a 2-week lockdown of default strength (allowing only a kt = 25% of pre-COVID-19 contacts) is either enacted when the TTI (yellow lines) or the hospital (red lines) capacity limits are reached. While not in lockdown, people maintain a level of contacts of kt = 80%. Without a major change in these policies, repeated lockdowns will eventually cease to be necessary because of the growing immunity, and case numbers will decline in all scenarios. However, this decline would occur weeks earlier if case numbers are below TTI capacity and vaccine efficacy is high. (E and F) Growing immunity among the population will considerably increase the maximal, critical, level of contacts allowed for stabilization of case numbers for both strategies but more substantially if not exceeding TTI capacity limit. More contagious variants such as B.1.1.7 (with an assumed base reproduction number of 4.3) will require a lower level of contacts (dotted lines).
Low case numbers are greatly beneficial even in light of progressing vaccination programs. In the high–case number regime, only in the most optimistic scenario can the spread of SARS-CoV-2 be controlled without contact reductions after the vaccination program is finished (Fig. 5E, the full gray line reaches 100%). In all other scenarios, because of the dominance of more contagious (dotted lines) or immune escape variants lowering vaccine efficacy (lower row), an efficiently functioning TTI program is necessary to allow for a high level of contacts (Fig. 5, E and F, blue lines). Therefore, reaching low case numbers is complementary to the vaccination efforts and necessary to maximize the population’s freedom.
DISCUSSION
We demonstrated that between the two extremes of eradication and uncontrolled spread, a metastable regime of SARS-CoV-2 spreading exists. In such a regime, every person only has to reduce their contacts moderately. Simultaneously, case numbers can still be maintained robustly at low levels because the TTI system can operate efficiently. If this regime is within reach, then keeping case numbers below TTI capacity is a suitable strategy for the long-term control of COVID-19 (or other infectious diseases) that features low fatalities and a small societal burden. In addition, it maximizes the effect of large-scale pharmaceutical interventions (as vaccination programs).
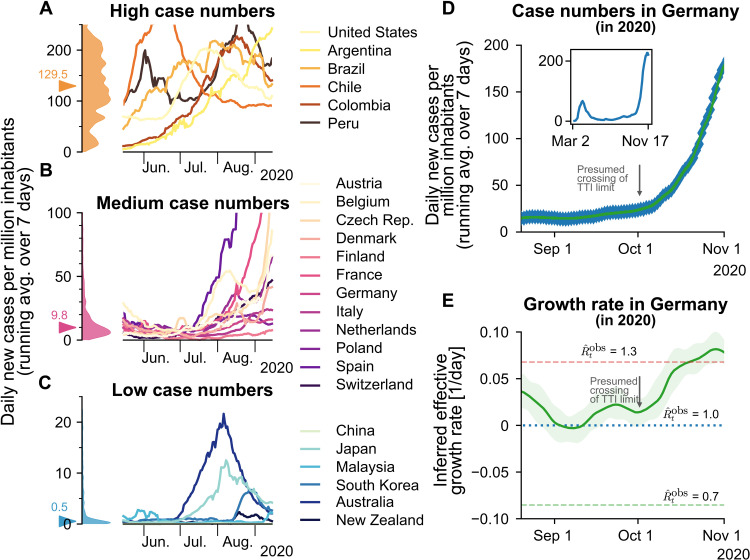
Among countries worldwide, variability in governmental policies and the chosen strategy to face COVID-19 substantially affect the levels of observed COVID-19 case numbers (see also Fig. 6 and note S1.1). Sustained high levels of more than 100 daily new cases per million have been observed in several (but not exclusively) American countries (Fig. 6A). This shows that high levels of daily new infections can be maintained. However, the stringency of interventions is similar to other countries (35), without signs of reaching population immunity. On the other hand, very low case numbers and even local eradication have been achieved by several South and East Asian countries, Australia, and New Zealand. At the time of writing, these countries profit from the absorbing state at zero SARS-CoV-2 infections, but maintaining this state requires substantial international travel restrictions (Fig. 6C). An intermediate level of case numbers could predominantly be observed over summer 2020 in Europe. Case numbers for many countries were typically around 10 daily new cases per million (Fig. 6B), although contacts were only mildly restricted. These stable numbers demonstrate that also, in practice, a regime below TTI capacity limits is maintainable. Nonetheless, in September, the spread substantially accelerated in several European countries, when case numbers began to exceed 20 to 50 daily new cases per million (fig. S5). Beyond these levels of case numbers, the TTI systems began to be overwhelmed, making control difficult, in line with our model’s results.
Fig. 6. Strategies of countries to fight SARS-CoV-2 differ widely and are reflected in case numbers.
(A) Strategies that involve little NPIs rely on the population to hinder the spread in a self-regulated manner and are often accompanied by high case numbers. (B) Strategies that aim to keep case numbers low through extensive TTI, combined with temporary lockdowns, can lead to medium case numbers. As TTI measures’ effectiveness depends on daily infections, case numbers can seemingly explode when the (hard-to-estimate) TTI capacity limit is exceeded. Many European countries managed to stabilize case numbers over summer 2020. However, stability was short lived, and they quickly saw case numbers rising faster than exponentially. (C) When the external influx is low or strategies used to reduce contacts are very effective, the stable regime can be reached. In this case, average case numbers are very low, and local outbreaks can be controlled well through local interventions. Raw data and preliminary visualizations were obtained from (62). (D and E) A substantial increase in Germany’s effective growth rate occurred during October, suggesting that regional TTI capacity limits were exceeded. (D) Observed case numbers were below 20 daily new cases per million until, presumably, a transition into the unstable regime took place over ∼4 weeks in October. The inset compares the extents of the so-called first and second waves. (E) Before October, the reproduction number was slightly above one (corresponding to a daily growth rate slightly above zero). More details are in fig. S4.
To focus our model on the general spreading dynamics, we made simplifying assumptions: We assumed that spreading happens homogeneously in the population, with neither regional nor age-related differences. In reality, heterogeneous spreading can lead to regionally differing case numbers, which illustrates the need for regional monitoring of the remaining TTI capacity to allow for early and targeted control measures. In our scenarios, we further assumed that the population’s behavior and subsequent contact reduction are constant over time (except during lockdown). Real situations are more dynamic, necessitating frequent reevaluations of the current restrictions and mitigation measures. We also assumed constant TTI effectiveness if below the capacity limit. However, if case numbers are very low, then all the available test and trace efforts could be concentrated on the remaining infection chains. This would further facilitate control at low case numbers. Overall, our analytical results describe the general behavior across countries well and identify the relevant factors for controlling the pandemic.
Quantitatively, our assumptions regarding the efficiency of TTI are in agreement with those of other modeling studies. Agent-based models with detailed contact structures (36, 37) and mean-field models (38–41) both agree that TTI measures are an essential contribution for the control of the pandemic but typically do not suffice alone. Their success strongly depends on their implementation: Fast testing, rigorous isolation, and a large proportion of traced contacts are essential. Given our informed assumptions about these parameters, our model shows that TTI can only compensate a basic reproduction number R0 of 3.3, if contagious contacts are also reduced to at most 61% (95% CI: [47, 76]) compared to pre-COVID-19. This is in agreement with the results of other studies (36, 37, 39, 42, 43).
The capacity limit of TTI plays a central role in the control of the spread but depends strongly on the local environment. The precise limit of TTI depends on several factors, including the number of available tests, personnel at the tracing units, potentially a tracing app (39), and the number of relevant contacts a person has on average. Already, the latter can easily differ by a factor of 10, depending on contact restrictions and cultural factors (44). We assumed that the capacity is reached at about 85 daily new cases per million for our scenarios, which is comparably high. Independent of the exact value, when this limit is approached, the risk of tipping over to uncontrolled spread strongly increases, and countermeasures should be taken without delay.
Given the large deviations of the capacity limit of TTI across regions, policy-makers should monitor local health authorities’ and tracing agencies’ capacity instead of relying on fixed limits. Health authorities can also assess whether a local outbreak is controlled or whether infection chains cannot be traced anymore, allowing an early and adaptive warning system. However, one can safely state that daily case numbers larger than 85 per million (corresponding to our modeled limit) are above the capacity limit of TTI programs in Europe, therefore requiring, in any case, further restrictions to reach controllable levels.
Even given the ongoing vaccination campaigns, a low level of case numbers below TTI capacity limits remains essential. We find that during and after the campaigns, TTI still greatly facilitates the containment of COVID-19. The vaccinations’ exact effect depends on several hard-to-model factors. It can change with newly emerging variants of the virus, which can be more contagious, more severe, or escape the immune response. In our analysis of the effect of vaccination, we also neglected age and high-risk-group distributions and contact networks in the population, the exact design of national vaccination plans, or the differential efficacy of vaccines against infection and severe disease. Some of these factors were taken into account in other publications (12–14). However, the long-term success of vaccinations alone remains hard to predict. Thus, it is sensible to accompany mass vaccinations to achieve low case numbers in the vaccine rollout and the time beyond.
Our results show that a stable equilibrium at low case numbers can be maintained with a moderate contact reduction of about 40% less contagious contacts compared to pre–COVID-19. In terms of our parameters, this translates to a maximum, critical, level of contacts of 61% (95% CI: [47, 76]). This level of contacts can be achieved with preventive mitigation measures, as shown by studies analyzing the effectiveness of NPIs during the first wave (17, 26, 27, 45, 46). Restrictions on the maximum size of gatherings already lead to an effective reduction in the range of 10 to 40% (17, 26, 27, 46). Improved hygiene, frequent ventilation of rooms, and the compulsory use of masks can further reduce the number of infectious contacts [by a factor that is more difficult to estimate (47, 48)]. Overall, until mass vaccination plans have been deployed worldwide and available vaccines have been shown to be successful against emerging variants, the regime of low case numbers is very promising for a mid- and long-term management of the pandemic, as it poses the least burden on economy and society.
On the other hand, stabilizing the spread at higher levels of case numbers (e.g., at the hospital capacity limit) requires more stringent and more frequent NPIs because the TTI system cannot operate efficiently. Examples of more stringent measures are the closure of schools and public businesses, stay-at-home orders, and contact ban policies (17, 26, 45).
In conclusion, this paper recommends reaching and maintaining low case numbers that allow efficient TTI measures complementary to pharmaceutical interventions. To this end, it is mandatory to counteract local super-spreading events (or an acute influx of infections) as early as possible and to sustain a sufficient level of mitigation measures. If low case numbers are reached and maintained throughout Europe, it will be possible to lift restrictions moderately in the medium term, and we will be better prepared for the emergence of future variants of concerns.
METHODS
Model overview
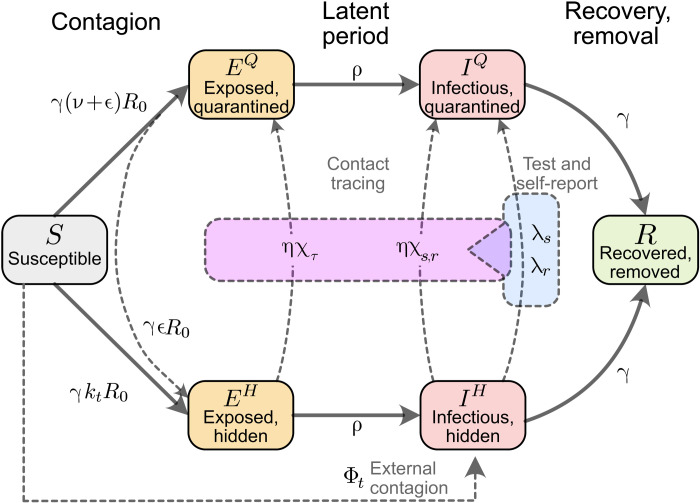
We model the spreading dynamics of SARS-CoV-2 as the sum of contributions from two pools of infectious individuals, i.e., quarantined-isolated IQ and hidden nonisolated IH individuals, while also modeling the infectivity timeline through the incorporation of compartments for individuals exposed to the virus (EQ, EH), following an SEIR-like formalism. The quarantined infectious pool (IQ) contains cases revealed through testing or by contact tracing and subsequently sent to quarantine/isolation to avoid further contacts as much as possible. In contrast, in the hidden infectious pool (IH), infections spread silently and only become detectable when individuals develop symptoms and get tested, via random testing in the population or as part ofthe chain of contacts of recently identified individuals. This second pool (IH) is called the hidden pool; individuals in this pool are assumed to exhibit the general population’s behavior, thus of everyone who is not aware of being infected. Healthy individuals that can be infected belong to the susceptible pool S. At the same time, we assume that, after they recover and for the relatively short time frame here studied, they remain immunized in the R compartment (for a graphical representation of the model, see Fig. 7). We model the mean-field interactions between compartments by transition rates, determining the time scales involved. These transition rates can implicitly incorporate both the disease’s time course and the delays inherent to the TTI process. Individuals exposed to the virus become infectious after the latent period, modeled by the transition rate ρ. We distinguish between symptomatic and asymptomatic carriers; this is central when exploring different testing strategies (as detailed below). We also include the effects of noncompliance to TTI measures, modeled as a higher asymptomatic ratio, and imperfect contact tracing, including an explicit delay between testing and contact tracing of contacts. In the different scenarios analyzed, we include a nonzero influx Φt of new cases that acquired the virus from outside. Although this influx makes a complete eradication of SARS-CoV-2 impossible, different outcomes in the spreading dynamics might arise depending on both contact intensity (contact level kt) and TTI. We then investigate the system’s stability and dynamics, aiming to control the spread with a low total number of cases without necessitating a too large reduction of infectious contacts.
Fig. 7. Flowchart of the complete model.
The solid blocks in the diagram represent different SEIR compartments for both hidden and quarantined individuals. Hidden compartments account for both symptomatic and asymptomatic carriers (as described in Methods). Solid lines represent the natural progression of the infection (contagion, latent period, and recovery). On the other hand, dashed lines account for imperfect quarantine and limited compliance, external factors, and TTI policies.
Spreading dynamics
Concretely, we use a modified SEIR-type model, where infected individuals can be either symptomatic or asymptomatic. They belong to hidden (EH, IH) or a quarantined (EQ, IQ) pools of infections, thus creating, in total, one compartment of susceptible (S), two compartments of exposed individuals (EH and EQ), four compartments of infectious individuals (IH, s, IH, a, IQ, s, and IQ, a), and one compartment for recovered/removed individuals (R).
New infections are asymptomatic with a ratio ξ; the others are symptomatic. In all compartments, individuals are removed with a rate γ because of recovery or death (see Table 1 for all parameters and Table 2 for all variables of the model).
Table 2. Model variables.
| Variable | Meaning | Units | Explanation |
| S | Susceptible pool | People | Noninfected people that may acquire the virus |
| EQ | Exposed pool (quarantined) | People | Total quarantined exposed people |
| EH | Exposed pool (hidden) | People | Total nontraced, nonquarantined exposed people |
| I H, s | Infectious pool (hidden, symptomatic) | People | Nontraced, nonquarantined people who are symptomatic |
| IH | Infectious pool (hidden) | People | Total nontraced, nonquarantined infectious people |
| IQ | Infectious pool (quarantined) | People | Total quarantined infectious people |
| N | New infections (total) | Cases day−1 | Given by: . |
| kt | Contact reduction | % | Reduction of infectious contacts, related to pre–COVID-19 times |
| Observed new infections (influx to traced pool) | Cases day−1 | Daily new cases, observed from the quarantined pool; delayed because of imperfect reporting and realistic contact tracing |
|
| Observed reproduction number | The reproduction number that can be estimated only from the observed cases: |
||
| N test | Number of cases found through testing | People | Cases can be found either through symptomatic or random testing . |
| N traced | Number of uncovered infections through tracing | People | This number is limited (depending on the reproduction number) by the maximal tracing capacity |
In the hidden pools, the disease spreads according to the population’s contact patterns, which can be expressed as a level kt of the intensity they had before COVID-19–related contact restrictions. Defining R0 as the base reproduction number without contact restrictions, the reproduction number of the hidden pool IH is given by ktR0. This reproduction number reflects the disease spread in the general population without testing-induced isolation of individuals. In addition, the hidden pool receives a mobility-induced influx Φt of new infections. Cases are removed from the hidden pool (i) when detected by TTI and put into the quarantined pool IQ or (ii) due to recovery or death.
The quarantined exposed and infectious pools (EQ, IQ) contain those infected individuals who have been tested positive and their positively tested contacts. Infectious individuals in IQ are (imperfectly) isolated; we assume that their contacts have been reduced to a fraction (ν + ϵ) of the ones they had in pre–COVID-19 times, of which only ν are captured by the tracing efforts of the health authorities. The subsequent infections remain quarantined, thus entering the EQ pool and, afterward, the IQ pool. The remaining fraction of produced infections, ϵ, are missed and act as an influx to the hidden pools (EH). Therefore, the overall reproduction number in the IQ pool is (ν + ϵ)R0.
As our model is an expanded SEIR model, it assumes postinfection immunity, which is a realistic assumption given the limited time frame considered in our analysis. Our model can also reflect innate immunity; one has to rescale the population or the reproduction number. The qualitative behavior of the dynamics is not expected to change.
Parameter choices and scenarios
For any testing strategy, the fraction of infections that do not develop any symptoms across the whole infection timeline is an important parameter, and this also holds for testing strategies applied to the case of SARS-CoV-2. In our model, this parameter is called ξap and includes, beside true asymptomatic infections ξ, also the effect of individuals that avoid testing (49). The exact value of the fraction of asymptomatic infections ξ, however, is still fraught with uncertainty, and it also depends on age (50). While early estimates were as high as 50% [for example, ranging from 26 to 63% (51)], these early estimates suffered from reporting bias and small sample sizes and sometimes included presymptomatic cases as well (52). Recent studies estimate the asymptomatic transmission to be more minor (53), estimates of the fraction of asymptomatic carriers range between 12% (52) and 33% (54).
Another crucial parameter for any TTI strategy is the reproduction number of the hidden infections. This parameter is, by definition, impossible to measure, but it is typically the main driver of the spreading dynamics. It depends mainly on the contact behavior of the population and ranges from R0 in the absence of contact restrictions to values below 1 during strict lockdown (17). Here, we decided to include instead contact level compared to the pre–COVID-19 baseline cts to represent the reproduction number of hidden infections . For the default parameters of our model, we evaluated different contact levels kt.
Testing and tracing strategies
We consider a testing and tracing strategy: symptom-driven testing and specific testing of traced contacts, with subsequent isolation (quarantine) of those who tested positive. Our model can also include random testing, but this case is only explored in Fig. 4 of this paper.
Symptom-driven testing is defined as applying tests to individuals presenting symptoms of COVID-19. In this context, note that noninfected individuals can have symptoms similar to those of COVID-19, as many symptoms are rather unspecific. Although symptom-driven testing suffers less from imperfect specificity, it can only uncover symptomatic cases that are willing to be tested (see below). Here, symptomatic, infectious individuals are transferred from the hidden to the traced pool at rate λs.
We define λs as the daily rate at which symptomatic individuals get tested among the subset who are willing to get tested because of surveillance programs or self-report. As default value, we use λs = 0.25, which means that, on average, an individual willing to get tested that develops COVID-19–specific symptoms would get a test within 4 days from the end of the latency period. Testing and isolation happen immediately in this model, but their report into the observed new daily cases is delayed and so is the tracing of their contacts.
Tracing contacts of positively tested infectious individuals presents a very specific test strategy and is expected to be effective in breaking the infection chains if contacts self-isolate sufficiently quickly (36, 55, 56). However, as every implementation of a TTI strategy is bound to be imperfect, we assume that only a fraction η < 1 of all contacts can be traced. These contacts, if tested positive, are then transferred from the hidden to the quarantined infectious pools (IH → IQ) with an average delay of τ = 2 days. The parameter η effectively represents the fraction of secondary and tertiary infections that are found through contact tracing. As this fraction decreases when the delay between testing and contact tracing increases, we assumed a default value of η = 0.66, i.e., on average, only two-thirds of subsequent offspring infections are prevented. Contact tracing is mainly done manually by the health authorities in Germany. This limits the maximum number of new cases observed through testing Ntest, for which contact tracing is still functional.
Random testing is defined here as applying tests to individuals irrespective of their symptom status or whether they belonged to the contact chain of other infected individuals. In our model, random testing transfers infected individuals from the hidden to the quarantined infectious pools with a fixed rate λr, irrespective of whether they are showing symptoms or not. In reality, random testing is often implemented as situation-based testing for a subgroup of the population, e.g., at a hotspot, for groups at risk, or for people returning from travel. These situation-based strategies would be more efficient than the random testing assumed in this model, which may be unfeasible at a country level because of testing limitations (15).
Lockdown modeling
To assess the effectiveness of lockdowns in the broad spectrum of contact-ban governmental interventions, we model how the reduction of contacts and the duration of such restrictive regimes help lower case numbers. We model contact reductions as reductions in the reproduction number of the hidden population, which, for these matters, is presented as percentages of the basic reproduction number R0, which sets the pre–COVID-19 baseline for the number of close contacts.
For the sake of simplicity, we assume that the lockdown scenarios have three stages: (i) an uncontrolled regime, where the TTI capacity is overwhelmed because of high case numbers and unsustainable contact levels, reflected by a high value of kt and a high influx of infections Φt. (ii) Lockdown is enacted, imposing a strong reduction of contacts, leading to lower values of kt, and borders closing, leading to a lower influx of Φt. (iii) Measures are relaxed, allowing higher levels of contacts kt and restoring international transit. All the changes between the different regimes i→ii→iii are modeled as linear ramps for both parameters, which take Dramp = 7 days to reach their set point. The duration of the lockdown, namely, the time frame between the start of the restrictive measures and the beginning of their relaxation, is measured in weeks. Its default length, for analysis purposes, is DL = 4 weeks. These values have been chosen following the results of (27), where the first effects of an NPI were seen after 7 days and the maximum effect was seen after 4 weeks.
Model equations
The contributions of the spreading dynamics and the TTI strategies are summarized in the equations below. They govern the dynamics of case numbers between the different SEIR pools, both hidden (nonisolated) and quarantined. We assume a regime where most of the population is susceptible, and the time frame analyzed is short enough to assume postinfection immunity. Thus, the dynamics are completely determined by the spread [characterized by the reproduction numbers ktR0 and (ν + ϵ)R0], the transition from exposed to infectious (at rate ρ), recovery (characterized by the recovery rate γ), external influx Φt, and the impact of the TTI strategies
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
Initial conditions
Let x be the vector collecting the variables of all different pools
| (10) |
We assume a population size of M = 106 individuals, so that ∑i ≠ 6xi = M, and a prevalence of I0 = 200 infections per million, so that IQ(0) = I0. Assuming that the hidden amount of infections is in the same order of magnitude I0, we would have IH(0) = I0, IH, s(0) = (1 − ξ)I0. We would expect the exposed individuals to scale with ktR0I0, but we rather assume them to have the same size of the corresponding infectious pool. To calculate the initially susceptible individuals, we use S(0) = 1 − ∑i ≠ {1,6}xi.
Effect of delays and capacity limit on the effectiveness of TTI strategies
In this section, we discuss further details on the derivation of the different parameters and variables involved in Eqs. 2 to 9. First, as we assume contact tracing to be effective after a delay of τ days, some of the individuals who acquired the infection from those recently tested might have also become infectious by the time of tracing. Moreover, a fraction of those who became infectious might also have been tested by the tracing time, should they have developed symptoms.
Furthermore, we give explicit forms for Ntest and Ntraced the number of cases identified by testing and contact tracing, respectively. When surpassing TTI capacity, we assume that both testing and contact tracing change their dynamics simultaneously. This happens when the daily amount of cases identified by testing Ntest overpasses the TTI threshold . After being overwhelmed, the overhead testing would change its rate λs → λs′, as only patients with a more specific set of symptoms would be tested. Nonetheless, the contact tracing efforts can only follow the contacts of those observed cases, identifying a fraction η of the offspring infections that they produced in their infectious period spent in unawareness of their state. The possibility of random testing is analyzed in note S1.6.
Limited testing capacity leading to lower testing rates
In the first stages of an outbreak, individuals with any symptoms from the broad spectrum of COVID-19–related symptoms would be tested, disregarding how specific those symptoms are. At this stage, we assume that the rate at which symptomatic individuals are tested is λs, such that the number of individuals identified through testing (which, for simplicity, is assumed to be solely symptom-driven, i.e., λr = 0) is given by
| (11) |
If, in addition, some random testing, independent of symptomatic status, is performed (λr ≠ 0), then . For this case see note S1.6.
When reaching the daily number of positive tests, the testing capacity is reached. We then assume that further tests are only carried out for a more specific set of symptoms, leading to a smaller fraction of the tested population. We, therefore, implement the testing capacity as a soft threshold. Assuming that after reaching , the testing rate for further cases would decrease to λs′, the testing term Ntest would be given by
| (12) |
where represent the size of the infectious-symptomatic, hidden pool, i.e., .
Modeling the number of traced individuals
To calculate the number of traced individuals, we assume that a fraction η of the newly tested individuals’ contacts, and therefore their offspring infections, will be traced and subsequently quarantined. However, in the presence of TTI, individuals stay, on average, a shorter amount of time in the infectious pool because they are quarantined before recovering. Therefore, the number of offspring infections has to be corrected by a factor, the average residence time in the infectious pool. For the case λr = 0, the average residence time is , as IH, s is emptied by , i.e., with a rate γ + λs. The average residence time in the absence of TTI (natural progression of the disease) is . Dividing these two times gives us the wanted correction factor. Thus, the number of traced persons Ntraced at time t is a fraction η from the offspring infections generated during the residence time, per each individual
| (13) |
where Rt − τ represents the effective reproduction number
| (14) |
In other words, the number of infectious individuals found by contact tracing at time t are a fraction η of the number of offspring infections generated by individual while they were untested , times the number of individuals tested τ days ago Ntest(t − τ). However, when the TTI capacity is overwhelmed, we assume that the number of traced individuals is limited, that only the contacts of individuals (already introduced in the previous section) can be traced
| (15) |
Individuals becoming infectious or being tested by the time of tracing
The traced individuals are removed from either the exposed hidden pool EH or from the infectious hidden pool IH after a delay of τ days after testing. As we assume a tracing delay τ of only 2 days, a fraction of the traced individuals would still be in exposed compartments by the time of contact tracing. However, some might already become infectious by that time. To calculate the exact fraction of individuals remaining in the hidden exposed pool by the time of tracing, we proceed as follows. Let s ∈ Iτ = [0, τ] be the time elapsed from the moment of testing. The emptying of the normalized exposed compartment (denoted ) due to progression to the infectious stage follows first-order kinetics
| (16) |
The solution of Eq. 16 is given by . Therefore, we define χτ as the fraction of the traced individuals remaining in the EH compartment at s = τ
| (17) |
The remaining individuals are removed from the infectious compartment, which are then simply described by the fraction
| (18) |
This, however, only holds for the asymptomatic hidden infectious pool. For the symptomatic hidden pool IH, s, we do not want to remove the individuals who have already been tested, as they would be removed twice. For modeling the fraction of nontested individuals remaining in the normalized symptomatic infectious compartment (denoted ), we couple two first-order kinetics
| (19) |
The solution of Eq. 19 depends on whether λs = ρ or not. The solution at s = τ, which is the fraction of traced individuals removed from IH, s, is given by
| (20) |
For the case λr ≠ 0, the reader is referred to note S1.6.
Including the effects of ongoing vaccination campaigns
To incorporate the effects of COVID-19 vaccination programs in our model, we made some simplifying assumptions. First, we assume that vaccinated individuals have a probability κ of not being infected even if they have a contact with somebody infectious and then not contributing to the spreading dynamics. We define this parameter as the “vaccine efficacy against infection,” which has been reported to be around 50 to 90% for available vaccines (32–34). Thus, they can be assumed to have developed perfect immunity and therefore can be removed from the susceptible (S) and put into the removed compartment (R). The assumption above also implies that these individuals would not take part in the TTI scheme, which would resemble the growing trend of “vaccination passports.” Second, we assume a logistically increasing daily vaccination rate v(t) consistent with the projections in the European Union and assume that 70% of the total population gets vaccinated (see Fig. 5, B and E). This would, e.g., in Germany, amount to roughly 80% of the adult population (16+ years old) accepting the offer of vaccination, since as of now, none of the available vaccines is approved for children. We find that efficient TTI can substantially enhance the effect of the growing immunity.
To include gradually growing immunity due to an ongoing vaccination campaign, we modify Eq. 2 with an additional term −κ · v(t), as well as Eq. 9 with a +κ · v(t), with a daily vaccination rate
| (21) |
centered at t = 0, which denotes the start of the vaccinations. This logistic increase in vaccination rates and parameters involved was adapted from (13) and roughly mirrors the projected vaccinations in the European Union (projections dated to the beginning of February 2021). The factor 9.3 × 103 is determined assuming that after tref = 220 days, 70% of the population would be vaccinated. Using as reference the age distribution of Germany, the above would amount to roughly 80% of the adult population (16+ years old) accepting the offer of vaccination. After that time, for simplicity, we assume that the vaccination stops [and therefore v(t) = 0, for t > 220].
This treatment of the vaccination is simplistic. In reality, most currently available vaccines imply receiving two doses in the span of a few weeks, where the first only gives partial protection. Furthermore, vaccinated individuals need some time to develop a proper immune response after receiving the vaccine (57), in which they can still get infected. We also do not incorporate the efficacy of vaccines against a severe course of the disease or death. Since vaccinated but yet infected individuals would have a lower chance of being admitted to the hospital, this would falsify our assumption that hospital capacity can be adequately measured by case numbers alone. As more and more of the daily new infections correspond to individuals already vaccinated, hospitals would only fill up at higher case numbers. To include this effect, the distribution of high-risk groups in the population and the prioritized vaccination programs would have to be taken into account. Including all this is beyond the scope of this work. We addressed those in a separate work, building on the results presented herein (13). However, this simplified implementation is sufficient for our qualitative assessments.
Central epidemiological parameters that can be observed
In the real world, the disease spread can only be observed through testing and contact tracing. While the true number of daily infections N is a sum of all new infections in the hidden and traced pools, the observed number of daily infections is the number of new infections discovered by testing, tracing, and surveillance of the contacts of those individuals in the quarantined infectious pool IQ, delayed by a variable reporting time. This includes internal contributions and contributions from testing and tracing
| (22) |
| (23) |
where ⊛ denotes a convolution and is an empirical probability mass function that models a variable reporting delay, inferred from German data (as the Robert Koch Institute reports the date the test is performed, the delay until the appearance in the database can be inferred): The total delay between testing and reporting a test corresponds to 1 day more than the expected time the laboratory takes for obtaining results, which is defined as follows: from testing, 50% of the samples would be reported the next day, 30% would be reported the second day, 10% would be reported the third day, and further delays complete the remaining 10%, which, for simplicity, we will truncate at day 4. Considering the extra day needed for reporting, the probability mass function for days 0 to 5 would be given by . The spreading dynamics are usually characterized by the observed reproduction number , which is calculated from the observed number of new cases . We here use the definition underlying the estimates that Robert Koch Institute publishes, the official body responsible for epidemiological control in Germany (58): The reproduction number is the relative change of daily new cases N separated by 4 days (the assumed serial interval of COVID-19)
| (24) |
In contrast to the original definition of (58), we do not need to remove real-world noise effects by smoothing this ratio.
Numerical calculation of solutions and critical values
The numerical solution of the delay differential equations (DDEs) governing our model were obtained using a versatile solver that tracks discontinuities and integrates with the explicit Runge-Kutta (2,3) pair, @dde23 implemented in MATLAB (version 2020a), with default settings. This algorithm allows the solution of nonstiff systems of differential equations in the shape y′(t) = f(t, y(t), y(t − τ1), …, y(t − τk), for a set of discrete lags . Suitability and details on the algorithm are further discussed in (59).
To derive the tipping point between controlled and uncontrolled outbreaks (e.g., critical, minimal required contact reduction for both stability and metastability) and to plot the stability diagrams, we used the @fzero MATLAB function, and the linear approximation of the system of DDE (3)–(7) for the limit. This function uses a combination of bisection, secant, and inverse quadratic interpolation methods to find the roots of a function. For instance, following the discussion of note S1.2, the different critical values for the contact reduction were determined by systematically solving the nonlinear eigenvalues problem for stability (60), where the solution operation was approximated with a Chebyshev differentiation matrix (61).
We also study the effect of dividing the exposed compartment into three subcompartments, thereby reducing the variability of the latent period distribution (understood as the distribution of waiting times from being infected until becoming infectious). We explored this extended system’s linear stability in note S1.8 and confirmed that using a single compartment efficiently characterizes the tipping points.
Acknowledgments
We thank M. Brinkmann and Á. Olivera-Nappa for helpful comments and encouraging feedback. We thank M. Loidolt, M. Wibral, J. Zierenberg, J. Wagner, and A. Sanchez for carefully reading, commenting, and improving the manuscript. We thank the Priesemann group for exciting discussions and valuable input. Funding: All authors received support from the Max Planck Society (Max-Planck-Gesellschaft MPRG-Priesemann). S.C. acknowledges funding by the Centre for Biotechnology and Bioengineering (CeBiB; PIA project FB0001, ANID, Chile). J.D. and F.P.S. acknowledge funding by SMARTSTART, the joint training program in computational neuroscience by the VolkswagenStiftung and the Bernstein Network. S.B.M. and S.B. were financially supported by the German Federal Ministry of Education and Research (BMBF) as part of the Network University Medicine (NUM), project egePan (funding code: 01KX2021). Author contributions: Conceptualization: S.C., J.D., and V.P. Methodology: S.C., J.D., and V.P. Software: S.C. and S.B.M. Validation: S.C., J.D., S.B.M., S.B., and V.P. Formal analysis: S.C., J.D., S.B.M., F.P.S., S.B., and V.P. Investigation: S.C., J.D., S.B.M., F.P.S., and S.B. Writing (original draft): S.C., J.D., S.B.M., F.P.S., and V.P. Writing (review and editing): S.C., J.D., S.B.M., F.P.S., S.B., and V.P. Visualization: S.C., F.P.S., and S.B.M. Supervision: V.P. Competing interests: V.P. is currently active in various groups to advise the government. The authors declare that they have no other competing interests. Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials. Raw data and preliminary visualizations of Fig. 6 and figs. S4 and S5 were obtained from (62). Analysis code is available in https://github.com/Priesemann-Group/covid19_metastability and permanently stored in https://doi.org/10.5281/zenodo.5220793 (63). In addition, an interactive platform to simulate scenarios different from those presented here is available at http://covid19-metastability.ds.mpg.de/.
Supplementary Materials
This PDF file includes:
Note S1
Figs. S1 to S6
Tables S1 to S3
References
REFERENCES AND NOTES
- 1.Randolph H. E., Barreiro L. B., Herd immunity: Understanding COVID-19. Immunity 52, 737–741 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Levin A. T., Hanage W. P., Owusu-Boaitey N., Cochran K. B., Walsh S. P., Meyerowitz-Katz G., Assessing the age specificity of infection fatality rates for COVID-19: Systematic review, meta-analysis, and public policy implications. Eur. J. Epidemiol. 35, 1123–1138 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Alwan N. A., Burgess R. A., Ashworth S., Beale R., Bhadelia N., Bogaert D., Dowd J., Eckerle I., Goldman L. R., Greenhalgh T., Gurdasani D., Hamdy A., Hanage W. P., Hodcroft E. B., Hyde Z., Kellam P., Kelly-Irving M., Krammer F., Lipsitch M., McNally A., McKee M., Nouri A., Pimenta D., Priesemann V., Rutter H., Silver J., Sridhar D., Swanton C., Walensky R. P., Yamey G., Ziauddeen H., Scientific consensus on the COVID-19 pandemic: We need to act now. Lancet 396, e71–e72 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Fraser E., Long term respiratory complications of COVID-19. BMJ 370, m3001 (2020). [DOI] [PubMed] [Google Scholar]
- 5.Greenhalgh T., Knight M., Ćourt C. A., Buxton M., Husain L., Management of post-acute COVID-19 in primary care. BMJ 370, m3026 (2020). [DOI] [PubMed] [Google Scholar]
- 6.Topol E. J., COVID-19 can affect the heart. Science 370, 408–409 (2020). [DOI] [PubMed] [Google Scholar]
- 7.Priesemann V., Brinkmann M. M., Ciesek S., Cuschieri S., Czypionka T., Giordano G., Gurdasani D., Hanson C., Hens N., Iftekhar E., Kelly-Irving M., Klimek P., Kretzschmar M., Peichl A., Perc M., Sannino F., Schernhammer E., Schmidt A., Staines A., Szczurek E., Calling for pan-European commitment for rapid and sustained reduction in SARS-CoV-2 infections. Lancet 397, 92–93 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.A. Scherbina, Determining the optimal duration of the COVID-19 suppression policy: A cost-benefit analysis (2019); https://ssrn.com/abstract=3562053.
- 9.Xiong J., Lipsitz O., Nasri F., Lui L. M., Gill H., Phan L., Chen-Li D., Iacobucci M., Ho R., Majeed A., McIntyre R. S., Impact of COVID-19 pandemic on mental health in the general population: A systematic review. J. Affect. Disord. 277, 55–64 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Li R., Pei S., Chen B., Song Y., Zhang T., Yang W., Shaman J., Substantial undocumented infection facilitates the rapid dissemination of novel coronavirus (SARS-CoV-2). Science 368, 489–493 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Van Doremalen N., Bushmaker T., Morris D. H., Holbrook M. G., Gamble A., Williamson B. N., Tamin A., Harcourt J. L., Thornburg N. J., Gerber S. I., Lloyd-Smith J. O., de Wit E., Munster V. J., Aerosol and surface stability of SARS-CoV-2 as compared with SARS-CoV-1. N. Engl. J. Med. 382, 1564–1567 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Moore S., Hill E. M., Tildesley M. J., Dyson L., Keeling M. J., Vaccination and non-pharmaceutical interventions for COVID-19: A mathematical modelling study. Lancet Infect. Dis. 21, 793–802 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.S. Bauer, S. Contreras, J. Dehning, M. Linden, E. Iftekhar, S. B. Mohr, Á. Olivera-Nappa, V. Priesemann, Relaxing restrictions at the pace of vaccination increases freedom and guards against further COVID-19 waves in Europe. arXiv:2103.06228 [q-bio.PE] (2021). [DOI] [PMC free article] [PubMed]
- 14.Contreras S., Priesemann V., Risking further COVID-19 waves despite vaccination. Lancet Infect. Dis. 21, 745–746 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Contreras S., Dehning J., Loidolt M., Zierenberg J., Spitzner F. P., Urrea-Quintero J. H., Mohr S. B., Wilczek M., Wibral M., Priesemann V., The challenges of containing SARS-CoV-2 via test-trace-and-isolate. Nat. Commun. 12, 378 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Linden M., Mohr S. B., Dehning J., Mohring J., Meyer-Hermann M., Pigeot I., Schöbel A., Priesemann V., Case numbers beyond contact tracing capacity are endangering the containment of COVID-19. Dtsch. Arztebl. Int. 117, 790–791 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Dehning J., Zierenberg J., Spitzner F. P., Wibral M., Neto J. P., Wilczek M., Priesemann V., Inferring change points in the spread of COVID-19 reveals the effectiveness of interventions. Science 369, eabb9789 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Hethcote H. W., The mathematics of infectious diseases. SIAM Rev. 42, 599–653 (2000). [Google Scholar]
- 19.Zhao S., Lin Q., Ran J., Musa S. S., Yang G., Wang W., Lou Y., Gao D., Yang L., He D., Wang M. H., Preliminary estimation of the basic reproduction number of novel coronavirus (2019-nCoV) in china, from 2019 to 2020: A data-driven analysis in the early phase of the outbreak. Int. J. Infect. Dis. 92, 214–217 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Alimohamadi Y., Taghdir M., Sepandi M., Estimate of the basic reproduction number for COVID-19: A systematic review and meta-analysis. J. Prev. Med. Public Health 53, 151–157 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.J. P. La Salle, The Stability of Dynamical Systems (SIAM, 1976). [Google Scholar]
- 22.Wilting J., Priesemann V., Inferring collective dynamical states from widely unobserved systems. Nat. Commun. 9, 2325 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Keeling M. J., Guyver-Fletcher G., Holmes A., Dyson L., Tildesley M. J., Hill E. M., Medley G. F., Precautionary breaks: Planned, limited duration circuit breaks to control the prevalence of COVID-19. medRxiv, 2020.10.13.20211813 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Mahase E., COVID-19: Experts recommend two week circuit break to reduce transmission in the UK. BMJ 371, m4038 (2020). [DOI] [PubMed] [Google Scholar]
- 25.Kmietowicz Z., Covid-19: “There is no alternative,” says Johnson, announcing new restrictions for England. BMJ 371, m4247 (2020). [DOI] [PubMed] [Google Scholar]
- 26.Brauner J. M., Mindermann S., Sharma M., Johnston D., Salvatier J., Gavenčiak T., Stephenson A. B., Leech G., Altman G., Mikulik V., Norman A. J., Monrad J. T., Besiroglu T., Ge H., Hartwick M. A., Teh Y. W., Chindelevitch L., Gal Y., Kulveit J., Inferring the effectiveness of government interventions against covid-19. Science 371, eabd9338 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Li Y., Campbell H., Kulkarni D., Harpur A., Nundy M., Wang X., Nair H., The temporal association of introducing and lifting non-pharmaceutical interventions with the time-varying reproduction number (R) of SARS-CoV-2: A modelling study across 131 countries. Lancet Infect. Dis. 21, 193–202 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Holt E., Slovakia to test all adults for SARS-CoV-2. Lancet 396, 1386–1387 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Mina M. J., Parker R., Larremore D. B., Rethinking Covid-19 test sensitivity—A strategy for containment. N. Engl. J. Med. 383, e120 (2020). [DOI] [PubMed] [Google Scholar]
- 30.Larremore D. B., Wilder B., Lester E., Shehata S., Burke J. M., Hay J. A., Tambe M., Mina M. J., Parker R., Test sensitivity is secondary to frequency and turnaround time for COVID-19 screening. Sci. Adv. 7, eabd5393 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Kirkcaldy R. D., King B. A., Brooks J. T., COVID-19 and postinfection immunity: Limited evidence, many remaining questions. JAMA 323, 2245–2246 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Thompson M., Burgess J., Naleway A., Tyner H. L., Yoon S. K., Meece J., Olsho L. E. W., Caban-Martinez A. J., Fowlkes A., Lutrick K., Kuntz J. L., Dunnigan K., Odean M. J., Hegmann K. T., Stefanski E., Edwards L. J., Schaefer-Solle N., Grant L., Ellingson K., Groom H. C., Zunie T., Thiese M. S., Ivacic L., Wesley M. G., Lamberte J. M., Sun X., Smith M. E., Phillips A. L., Groover K. D., Yoo Y. M., Gerald J., Brown R. T., Herring M. K., Joseph G., Beitel S., Morrill T. C., Mak J., Rivers P., Harris K. M., Hunt D. R., Arvay M. L., Kutty P., Fry A. M., Gaglani M., Interim estimates of vaccine effectiveness of BNT162b2 and mRNA-1273 COVID-19 vaccines in preventing SARS-CoV-2 infection among health care personnel, first responders, and other essential and frontline workers—Eight U.S. locations, December 2020–March 2021. MMWR Morb. Mortal. Wkly. Rep. 70, 495–500 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Dagan N., Barda N., Kepten E., Miron O., Perchik S., Katz M. A., Hernán M. A., Lipsitch M., Reis B., Balicer R. D., BNT162b2 mRNA Covid-19 vaccine in a nationwide mass vaccination setting. N. Engl. J. Med. 384, 1412–1423 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Voysey M., Clemens S. A. C., Madhi S. A., Weckx L. Y., Folegatti P. M., Aley P. K., Angus B., Baillie V. L., Barnabas S. L., Bhorat Q. E., Bibi S., Briner C., Cicconi P., Collins A. M., Colin-Jones R., Cutland C. L., Darton T. C., Dheda K., Duncan C. J. A., Emary K. R. W., Ewer K. J., Fairlie L., Faust S. N., Feng S., Ferreira D. M., Finn A., Goodman A. L., Green C. M., Green C. A., Heath P. T., Hill C., Hill H., Hirsch I., Hodgson S. H. C., Izu A., Jackson S., Jenkin D., Joe C. C. D., Kerridge S., Koen A., Kwatra G., Lazarus R., Lawrie A. M., Lelliott A., Libri V., Lillie P. J., Mallory R., Mendes A. V. A., Milan E. P., Minassian A. M., Gregor A. M., Morrison H., Mujadidi Y. F., Nana A., O’Reilly P. J., Padayachee S. D., Pittella A., Plested E., Pollock K. M., Ramasamy M. N., Rhead S., Schwarzbold A. V., Singh N., Smith A., Song R., Snape M. D., Sprinz E., Sutherland R. K., Tarrant R., Thomson E. C., Török M. E., Toshner M., Turner D. P. J., Vekemans J., Villafana T. L., Watson M. E. E., Williams C. J., Douglas A. D., Hill A. V. S., Lambe T., Gilbert S. C., Pollard A. J.; Oxford COVID Vaccine Trial Group , Safety and efficacy of the ChAdOx1 nCoV-19 vaccine (AZD1222) against SARS-CoV-2: An interim analysis of four randomised controlled trials in Brazil, South Africa, and the UK. Lancet 397, 99–111 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.T. Hale, S. Webster, A. Petherick, T. Phillips, B. Kira, Oxford COVID-19 Government Response Tracker, Blavatnik School of Government (2020); www.fda.gov/media/136472/download. [DOI] [PubMed]
- 36.Kucharski A. J., Klepac P., Conlan A. J. K., Kissler S. M., Tang M. L., Fry H., Gog J. R., Edmunds W. J.; CMMID COVID-19 working group , Effectiveness of isolation, testing, contact tracing, and physical distancing on reducing transmission of SARS-CoV-2 in different settings: A mathematical modelling study. Lancet Infect. Dis. 20, 1151–1160 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Kerr C. C., Mistry D., Stuart R. M., Rosenfeld K., Hart G. R., Núñez R. C., Cohen J. A., Selvaraj P., Abeysuriya R. G., Jastrzebski M., George L., Hagedorn B., Panovska-Griffiths J., Fagalde M., Duchin J., Famulare M., Klein D. J., Controlling COVID-19 via test-trace-quarantine. Nat. Commun. 12, 2993 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Fraser C., Riley S., Anderson R. M., Ferguson N. M., Factors that make an infectious disease outbreak controllable. Proc. Natl. Acad. Sci. U.S.A. 101, 6146–6151 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Ferretti L., Wymant C., Kendall M., Zhao L., Nurtay A., Abeler-Dörner L., Parker M., Bonsall D., Fraser C., Quantifying SARS-CoV-2 transmission suggests epidemic control with digital contact tracing. Science 368, eabb6936 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Lunz D., Batt G., Ruess J., To quarantine, or not to quarantine: A theoretical framework for disease control via contact tracing. Epidemics 34, 100428 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Sturniolo S., Waites W., Colbourn T., Manheim D., Panovska-Griffiths J., Testing, tracing and isolation in compartmental models. PLOS Comput. Biol. 17, e1008633 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Hellewell J., Abbott S., Gimma A., Bosse N. I., Jarvis C. I., Russell T. W., Munday J. D., Kucharski A. J., Edmunds W. J., Sun F., Feasibility of controlling COVID-19 outbreaks by isolation of cases and contacts. Lancet Glob. Health 8, e488–e496 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Davis E. L., Lucas T. C. D., Borlase A., Pollington T. M., Abbott S., Ayabina D., Crellen T., Hellewell J., Pi L.; CMMID COVID-19 working group, Medley G. F., Hollingsworth T. D., Klepac P., An imperfect tool: COVID-19‘test & trace’ success relies on minimising the impact of false negatives and continuation of physical distancing. medRxiv , 2020.06.09.20124008 (2020). [Google Scholar]
- 44.Van Bavel J. J., Baicker K., Boggio P. S., Capraro V., Cichocka A., Cikara M., Crockett M. J., Crum A. J., Douglas K. M., Druckman J. N., Drury J., Dube O., Ellemers N., Finkel E. J., Fowler J. H., Gelfand M., Han S., Haslam S. A., Jetten J., Kitayama S., Mobbs D., Napper L. E., Packer D. J., Pennycook G., Peters E., Petty R. E., Rand D. G., Reicher S. D., Schnall S., Shariff A., Skitka L. J., Smith S. S., Sunstein C. R., Tabri N., Tucker J. A., van der Linden S., van Lange P., Weeden K. A., Wohl M. J. A., Zaki J., Zion S. R., Willer R., Using social and behavioural science to support COVID-19 pandemic response. Nat. Hum. Behav. 4, 460–471 (2020). [DOI] [PubMed] [Google Scholar]
- 45.Hsiang S., Allen D., Annan-Phan S., Bell K., Bolliger I., Chong T., Druckenmiller H., Huang L. Y., Hultgren A., Krasovich E., Lau P., Lee J., Rolf E., Tseng J., Wu T., The effect of large-scale anti-contagion policies on the COVID-19 pandemic. Nature 584, 262–267 (2020). [DOI] [PubMed] [Google Scholar]
- 46.Sharma M., Mindermann S., Rogers-Smith C., Leech G., Snodin B., Ahuja J., Sandbrink J. B., Monrad J. T., Altman G., Dhaliwal G., Finnveden L., Norman A. J., Oehm S. B., Sandkühler J. F., Mellan T., Kulveit J., Chindelevitch L., Flaxman S., Gal Y., Mishra S., Brauner J. M., Bhatt S., Understanding the effectiveness of government interventions in Europe’s second wave of COVID-19. medRxiv, 2021.03.25.21254330 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Chu D. K., Akl E. A., Duda S., Solo K., Yaacoub S., Schünemann H. J.; COVID-19 Systematic Urgent Review Group Effort (SURGE) study authors , Physical distancing, face masks, and eye protection to prevent person-to-person transmission of SARS-CoV-2 and COVID-19: A systematic review and meta-analysis. Lancet 395, 1973–1987 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Howard J., Huang A., Li Z., Tufekci Z., Zdimal V., van der Westhuizen H.-M., von Delft A., Price A., Fridman L., Tang L.-H., Tang V., Watson G. L., Bax C. E., Shaikh R., Questier F., Hernandez D., Chu L. F., Ramirez C. M., Rimoin A. W., An evidence review of face masks against COVID-19. Proc. Natl. Acad. Sci. U.S.A 118, e2014564118 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.McDermott J. H., Newman W. G., Refusal of viral testing during the SARS-CoV-2 pandemic. Clin. Med. 20, e163–e164 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Lai C.-C., Liu Y. H., Wang C.-Y., Wang Y.-H., Hsueh S.-C., Yen M.-Y., Ko W.-C., Hsueh P.-R., Asymptomatic carrier state, acute respiratory disease, and pneumonia due to severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2): Facts and myths. J. Microbiol. Immunol. Infect. 53, 404–412 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Lavezzo E., Franchin E., Ciavarella C., Cuomo-Dannenburg G., Barzon L., Del Vecchio C., Rossi L., Manganelli R., Loregian A., Navarin N., Abate D., Sciro M., Merigliano S., De Canale E., Vanuzzo M. C., Besutti V., Saluzzo F., Onelia F., Pacenti M., Parisi S. G., Carretta G., Donato D., Flor L., Cocchio S., Masi G., Sperduti A., Cattarino L., Salvador R., Nicoletti M., Caldart F., Castelli G., Nieddu E., Labella B., Fava L., Drigo M., Gaythorpe K. A. M.; Imperial College COVID-Response Team, Brazzale A. R., Toppo S., Trevisan M., Baldo V., Donnelly C. A., Ferguson N. M., Dorigatti I., Crisanti A., Suppression of COVID-19 outbreak in the municipality of Vo, Italy. Nature 584, 425–429 (2020). [DOI] [PubMed] [Google Scholar]
- 52.Byambasuren O., Cardona M., Bell K., Clark J., McLaws M.-L., Glasziou P., Estimating the extent of asymptomatic COVID-19 and its potential for community transmission: Systematic review and meta-analysis. J. Assoc. Med. Microbiol. Infect. Dis. Canada 5, 223–234 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Cevik M., Kuppalli K., Kindrachuk J., Peiris M., Virology, transmission, and pathogenesis of SARS-CoV-2. BMJ 371, m3862 (2020). [DOI] [PubMed] [Google Scholar]
- 54.Pollán M., Pérez-Gómez B., Pastor-Barriuso R., Oteo J., Hernán M. A., Pérez-Olmeda M., Sanmartín J. L., Fernández-García A., Cruz I., de Larrea N. F., Molina M., Rodríguez-Cabrera F., Martín M., Merino-Amador P., Paniagua J. L., Muñoz-Montalvo J. F., Blanco F., Yotti R.; ENE-COVID Study Group , Prevalence of sars-cov-2 in spain (ene-covid): A nationwide, population-based seroepidemiological study. Lancet 396, 535–544 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Firth J. A., Hellewell J., Klepac P., Kissler S. M., Kucharski A. J., Spurgin L. G., Combining fine-scale social contact data with epidemic modelling reveals interactions between contact tracing, quarantine, testing and physical distancing for controlling COVID-19. medRxiv 10.1101/2020.05.26.20113720 (2020). [Google Scholar]
- 56.Kojaku S., Hébert-Dufresne L., Mones E., Lehmann S., Ahn Y.-Y., The effectiveness of backward contact tracing in networks. Nat. Phys. 17, 652–658 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Polack F. P., Thomas S. J., Kitchin N., Absalon J., Gurtman A., Lockhart S., Perez J. L., Pérez Marc G., Moreira E. D., Zerbini C., Bailey R., Swanson K. A., Roychoudhury S., Koury K., Li P., Kalina W. V., Cooper D., Frenck Jr. R. W., Hammitt L. L., Türeci Ö., Nell H., Schaefer A., Ünal S., Tresnan D. B., Mather S., Dormitzer P. R., Şahin U., Jansen K. U., Gruber W. C.; C4591001 Clinical Trial Group , Safety and efficacy of the bnt162b2 mrna covid-19 vaccine. N. Engl. J. Med. 383, 2603–2615 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.an der Heiden M., Hamouda O., Schätzung der aktuellen Entwicklung der SARS-CoV-2- Epidemie in Deutschland – Nowcasting. Epidemiologisches Bull. 2020, 10–15 (2020). [Google Scholar]
- 59.Shampine L. F., Thompson S., Solving ddes in matlab. Appl. Numer. Math. 37, 441–458 (2001). [Google Scholar]
- 60.Jarlebring E., Some numerical methods to compute the eigenvalues of a time-delay system using MATLAB. E-Delay System Letter 2, 155 (2008). [Google Scholar]
- 61.L. N. Trefethen, Spectral Methods in MATLAB (SIAM, 2000). [Google Scholar]
- 62.H. Ritchie, E. Mathieu, L. Rodés-Guirao, C. Appel, C. Giattino, E. Ortiz-Ospina, J. Hasell, B. Macdonald, D. Beltekian, M. Roser, Coronavirus pandemic (COVID-19), Our World in Data (2020); https://ourworldindata.org/coronavirus.
- 63.J. Dehning, Priesemann-Group/covid19_metastability. Zenodo (2021); 10.5281/zenodo.5220793. [DOI]
- 64.He X., Lau E. H. Y., Wu P., Deng X., Wang J., Hao X., Lau Y. C., Wong J. Y., Guan Y., Tan X., Mo X., Chen Y., Liao B., Chen W., Hu F., Zhang Q., Zhong M., Wu Y., Zhao L., Zhang F., Cowling B. J., Li F., Leung G. M., Temporal dynamics in viral shedding and transmissibility of COVID-19. Nat. Med., 1491–1493 (2020). [DOI] [PubMed] [Google Scholar]
- 65.Pan F., Ye T., Sun P., Gui S., Liang B., Li L., Zheng D., Wang J., Hesketh R. L., Yang L., Zheng C., Time course of lung changes on chest CT during recovery from 2019 novel coronavirus (COVID-19) pneumonia. Radiology 295, 200370 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Bar-On Y. M., Flamholz A., Phillips R., Milo R., SARS-CoV-2 (COVID-19) by the numbers. eLife 9, e57309 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Siegenfeld A. F., Bar-Yam Y., The impact of travel and timing in eliminating COVID-19. Commun. Phys. 3, 204 (2020). [Google Scholar]
- 68.P. Bittihn, R. Golestanian, Containment strategy for an epidemic based on fluctuations in the SIR model. arXiv:2003.08784 [q-bio.PE] (2020).
- 69.Salvatier J., Wiecki T. V., Fonnesbeck C., Probabilistic programming in Python using PyMC3. PeerJ Comput. Sci. 2, e55 (2016). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Note S1
Figs. S1 to S6
Tables S1 to S3
References