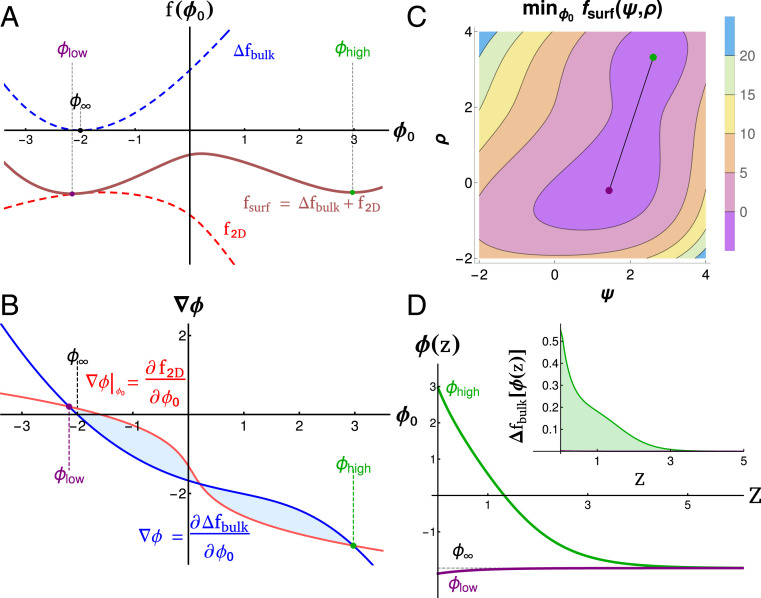
Fig. 5.

Landau theory of surface phases. (A) Bulk $\mathrm{\Delta }{f}_{bulk}$ (blue), membrane $f_{2\text{D}}$ (red, already minimized over $\psi ,\rho$), and surface $f_{surf}=\mathrm{\Delta }{f}_{bulk}+f_{2\text{D}}$ (brown) free energies as a function of surface polymer density ${\varphi }_0$. There are two energy minima, ${\varphi }_{low}$ and ${\varphi }_{high}$ in the combined $f_{surf}$ even in the absence of multiple minima in $\mathrm{\Delta }{f}_{bulk}$ or $f_{2\text{D}}$. (B) Gradient construction used to visualize solutions. Intersections of derivatives of $f_{2\text{D}}$ (red) and $\mathrm{\Delta }{f}_{bulk}$ (blue) give possible surface solutions ${\varphi }_{low}$ and ${\varphi }_{high}$. The free energy difference between these solutions is given by the area between these curves, visualized as the shaded regions. Changing the position or slope of surface or bulk lines changes the surface solutions. (C) Surface free energy $f_{surf}$ calculated over values of $\psi$ and $\rho$, minimized first over ${\varphi }_0$. Two minima (purple and green) correspond to surface compositions that minimize the free energy of the membrane and tethers along with their resulting contributions to bulk energy. (D) Density profiles and energy density (Inset) as a function of distance from the membrane $z$ for the two physical phases. Both ${\varphi }_{high}$ and ${\varphi }_{low}$ decay to the bulk density ${\varphi }_{\infty }$. This adds unfavorable contributions to the free energy $\mathrm{\Delta }{f}_{bulk}\left(\varphi \left(z\right)\right)$ that are balanced by contributions from $f_{surf}$.