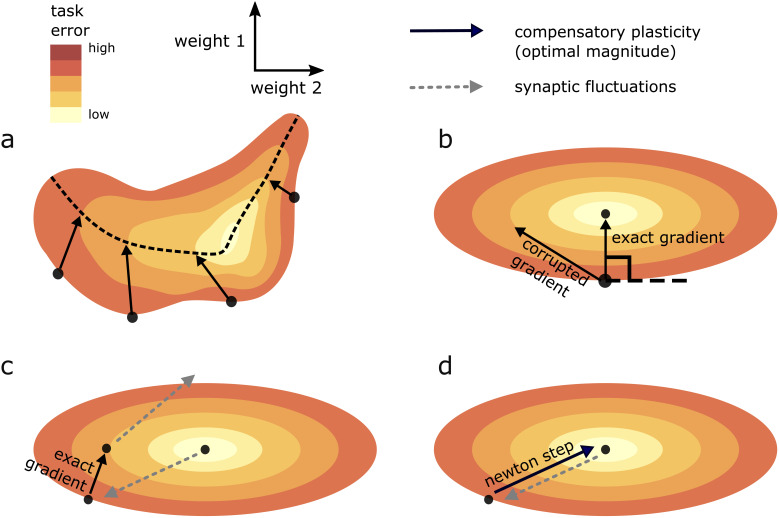
Figure 4. Geometric intuition for the optimal magnitude of different compensatory plasticity directions.

Colours depict level sets of the loss landscape. Elliptical level sets correspond to a quadratic loss function (which approximates any loss function in the neighbourhood of a local minimum). In c and d, we depict compensatory plasticity and synaptic fluctuations as sequential, alternating processes for illustrative purposes, although they are modelled as concurrent throughout the paper. (a) Compensatory plasticity directions locally decrease task error, so point from darker to lighter colours. Optimal magnitude is reached when the vectors ‘kiss’ a smaller level set, that is, intersect that level set while running parallel to its border. Increasing magnitude past this past this point increases task error, by moving network state to a higher-error level set. (b) If compensatory plasticity is parallel to the gradient (i.e. it enacts gradient descent), then it runs perpendicular to the border of the level set on which it lies (i.e. the tangent plane). This is shown explicitly for the ‘exact gradient’ direction of plasticity. The optimal magnitude of plasticity in this direction is smaller than that of a corrupted gradient descent direction, even though the former is more effective in reducing task error, because the exact gradient points in a more highly curved direction. (c) Synaptic fluctuations of a certain magnitude perturb the network state. The optimal magnitude of compensatory plasticity (in the exact gradient descent direction, for this example) is significantly smaller than that of the synaptic fluctuations, using the geometric heuristic explained in (a). If the magnitude of compensation increased to match the synaptic fluctuation magnitude there would be overshoot, and task error would converge to a higher steady state. (d) If compensatory plasticity mechanisms can perfectly calculate both the local gradient and hessian (curvature) of the loss landscape, then network state will move in the direction of the ‘Newton step’. In the quadratic case (elliptical level sets), this will directly ‘backtrack’ the synaptic fluctuations. Thus, the optimal magnitude of compensatory plasticity will be equal to that of the synaptic fluctuations. However, time delays in the sensing of synaptic fluctuations and limited precision of the compensatory plasticity mechanism will preclude this.