SARS-CoV-2 mutational cascades and the risk of hyper-exponential growth

Abstract

The emergence of novel SARS-CoV-2 variants of concern (VOC), in late 2020, with selective transmission advantage and partial immunity escape potential, has been driving further evolution in the pandemic. The timing of mutational evolution and its limits are thus of paramount importance in preparedness planning. Here, we present a model predicting the pattern of epidemic growth including the emergence of variants through mutation. It is based on the SEIR (Susceptible, Exposed, Infected, Removed) model, but its equations are modified according to the transmission parameters of novel variants. Since more transmissible strains will drive a further increase in the number of cases, they will also lead to further novel mutations. As one cannot predict whether there is a viral mutational evolutionary limit, we model a cascade that could lead to hyper-exponential growth (HEG) involving the emergence of even more transmissible mutants that could overwhelm any systematic response. Our results are consistent with the timing, since the beginning of the pandemic, of the concurrent and independent emergence of the VOCs. The current dominance of the Delta variant and the need for additional public health measures indicates some of the risks of a possible HEG. We examine conditions that favor the expected appearance of similar variants, thus enabling better preparedness and more targeted research.

1. Introduction

The SARS-CoV-2 pandemic entered a novel phase in 2021 with the gradual dominance of the variants of concern (VOC). Since, apart from theoretical projections, there is no blueprint about the ways a coronavirus pandemic will evolve (in space, time, and number of cases), and since we cannot ascertain whether there is a limit in the viral transmission, virulence, and immune escape potential, public authorities need to evaluate a range of possible trajectories in order to pre-emptively design public health response measures.

VOCs are defined as variants that possess important novel characteristics in terms of high virulence, transmission potential, reproduction number (R ₀), ability to infect previously low-risk groups like children, and resistance to the neutralizing effect of both serum from convalescent individuals and antibodies emerging post vaccination. As of August 2021, the World Health Organization has defined four SARS-CoV-2 variants as VOCs. Variant Alpha (PANGO lineage B.1.1.7/, formerly also known as 501Y.V1) was first isolated in the United Kingdom and exhibits markedly higher transmission potential as well as increased virulence. Variant Beta (PANGO lineage B.1.351/, formerly also known as 501Y.V2) was first isolated in patients from South Africa and is the most potent escape variant, reducing severalfold convalescent and vaccinated sera neutralizing potential. Gamma variant (PANGO lineage P.1/, formerly also known as 501Y.V3) was first isolated in patients originating from Brazil and possesses marked immunity resistance. Both Beta and Gamma exhibit moderately higher transmissibility. These three variants emerged independently but possess a common mutation, N501Y, conferring stronger adherence of the viral receptor binding domain (RBD) to host receptors. The fourth VOC, Delta variant (PANGO lineage B.1.617.2), does not possess such a mutation. Delta was first isolated in India and rapidly spread to dominance; it is characterized by a major increase in transmissibility (that could be attributed to the P681R mutation, neighboring the furin cleavage site and thus potentially inducing rapid cleavage) and possibly partial immune escape and vaccine breakthrough [[1], [2], [3], [4]] (Fig. 1 ). Other variants under surveillance are termed Variants of Interest.

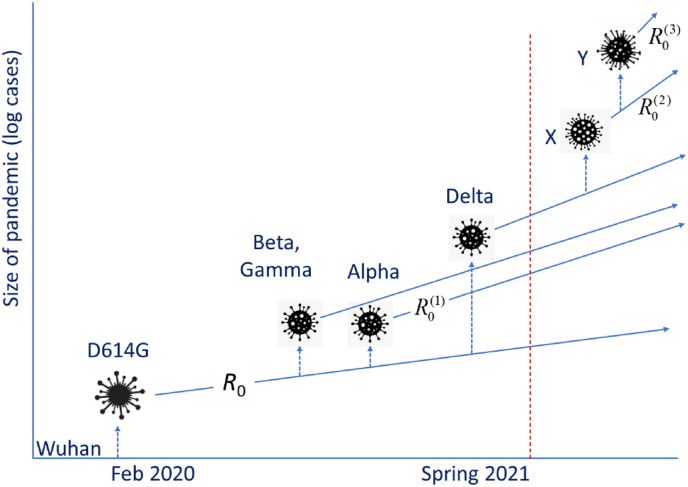
Fig. 1.

Schematic depiction of the evolution of the pandemic. Dotted arrows indicate mutations, while the straight lines depict the slope of the exponential growth in log-space. The original ‘Wuhan’ variant was replaced by D614G, which has spawned in turn several successful variants with a higher reproductive number (R₀⁽¹⁾). This is the current evolution of the pandemic. Future developments (to the right of the red broken line) could include the emergence of more variants (‘X’, ‘Y’ etc.), with even greater reproductive numbers (R₀⁽²⁾, R₀⁽³⁾ etc.).

It is well known that coronaviruses exhibit a lower mutation rate than other major viral pathogens, such as Influenza A. It has recently been demonstrated that coronavirus 229E, a cause of the common cold, needs roughly a decade in order to achieve adequate therapeutic escape (significantly slower than Influenza A/H3N2) [5]. Although most RNA viruses accumulate mutations as a result of their RdRp infidelity, SARS-CoV-2 was initially thought to be less prone to mutations, since its RdRp incorporates proofreading activity [6]. Unfortunately, soon after the expansion of the pandemic (February 2020), a mutation at position 314 of the ORF1b resulted in an amino acid change of the RdRp that led to an increase of subsequent mutations, as Pachetti et al. [7] argued, including those on the spike [8].

The mutation potential of the SARS-CoV-2 is magnified by the vast circulation of the virus during the pandemic over an extended period of time. Variant emergence is a global phenomenon that cannot be controlled simply by imposing strict public health measures at the local scale. For example, it has been shown that variant emergence and circulation in the US paralleled the worldwide viral incidence, instead of following the local epidemiology [9]. An increasing rate of infections itself increases the total number of mutations providing the opportunity for the emergence of new strains of even higher infectiousness. The resulting cascade effect could cause the dynamics to develop a hyper-exponential character. Hyper-exponential growth is essentially exponential growth with an increasing exponent. It is seen in the growth of the human population [10] and economy [11]; it is rarely observed in nature and appears only in evolutionary systems under selection for growth. It has also appeared in some models of genetic instability in neoplasms [12]. In the case of a growing pandemic, as more people become infected, the number of individual viruses does too, with it the total mutation rate, and with them the probability of emergence of a viable new variant. If this variant, in addition, has a higher reproductive number, R ₀, it will increase more rapidly than the original, eventually overtaking it. As a result, the next mutation of significance (conferring higher R ₀) is expected to derive from this new strain. We will thus observe the emergence and ascendance of higher-R ₀ strains. Less infectious variants, with low or negative growth rate, quickly fall behind. Now the epidemic spreads faster, with more infections, more mutations, and the emergence of ever more successful variants. This cascade rapidly moves the process into a hyper-exponential pattern of growth that continues until the epidemic runs out of susceptibles and the number of infected people starts to decline.

The actual emergence and spread of the new aggressive strains shows that such mutations in SARS-CoV-2 are indeed enjoying a selective advantage. Similarly, it can suggest the onset of a process deviating from exponential growth. By using a model of epidemic growth including mutations that enable increased R ₀, the purpose of this study is to examine how likely it is for this process to continue further into HEG in the pandemic of COVID-19. The possible disruptive aspects of HEG, should it happen, deserve scrutiny because they would involve at least greater numbers of cases, more rapid spread, stricter lockdowns, and larger vaccination coverage, to an even greater degree than caused by Delta variant.

Our approach uses a system of SEIR (Susceptible, Exposed, Infected, Removed) equations [13,14] modified to include new variants with variable transmission rates. We model the expansion of the disease in an immunologically naïve population. Selection is by growth rate alone, so that important mutations (leading to future VOCs) are based only on the conferring of higher transmission rates (Fig. 2 a) that lead to higher reproductive numbers.

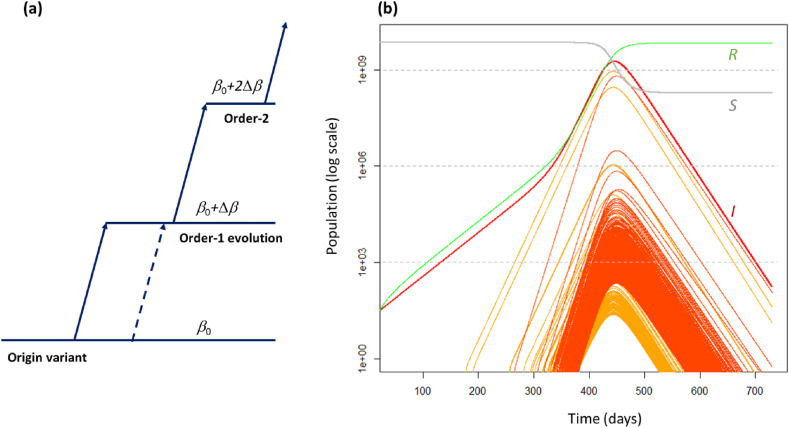
Fig. 2.

(a) Model of the mutating SEIR system used in this paper. Each variant may increase its transmission coefficient by changing its traits, one mutation at a time. If there are k successful mutations, this “order-k” change delivers an increase kΔβ in transmission coefficient. Other mutations of the original strain can create other order-1 variants at any time (broken lines). A single mutation cannot raise the transmission rate by more than Δβ. Thus, a variant cannot jump directly to order-2 or higher from the original. (b) Solutions of modified SEIR equations (Eq. (2)): the red curve is the total number of infectious individuals (I), the grey curve is the number of susceptibles (S), and the green curve is the number of removed (R). Pre-infectious numbers are not plotted. The yellow curves are the numbers of infectious people with order-1 strains of the disease while orange curves are for those of order-2 or higher. The initial values of the SEIR parameters were: E₀ = 27, I₀ = 0, S = 7 × 10⁹, R = 0, transmission rate β₀ = 4.57 × 10⁻¹² per day, and Δβ=0.9β₀. Latency time was 5.2 days and recovery time 14 days. The simulations covered a period of two years. The probability of a successful mutation is p = 10⁻⁵ per infected individual. The equations were solved using the Euler method with a step size Δt = 0.2 days.

2. Results

In Fig. 2b, we can see the epidemic growing initially at a rate of 0.031 per day, the average growth of the COVID-19 pandemic in 2020 [14]. The first mutant strains (orange curves) with greater “fitness” arise at day 180 and increase more rapidly than the initial strain. Three such order-1 variants (yellow curves) appear before the order-2 variants (orange curves) start to emerge, at day 270, and increase still more rapidly. This is the driving force beneath the upturn of the rate of infections after day 400. Together with this, there is a massive increase in the number of new successful variants (mostly first and second order) simply because of the huge number of cases overall. Some strains with very high growth rate can be seen in Fig. 2b but as they do not reach high numbers, they do not substantively alter the overall trajectory.

The probability p of a successful mutation determines the output of this model. There are three types of outcome. If the probability of a successful mutation is very small (p < 10⁻⁶ per infected person), the overall dynamics of the pandemic are not noticeably affected, despite new strains appearing. If it is large (p > 10⁻³), there is a strong cascade effect, with a marked curvature of the number of infectious individuals, implying sequential accelerations and HEG. Finally, for intermediate values of p, we tend to see the pattern of Fig. 2b, i.e., a large number of highly infectious strains dominated by a few variants.

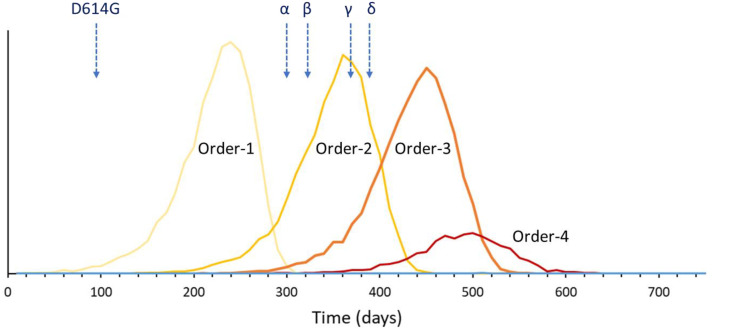
The distribution of times for the first emergence of an order-k variant, estimated using a Monte-Carlo approach, is shown in Fig. 3 . This figure is based on the results of 10,000 runs of the model. In general, order 1–3 variants always emerge, but order-4 variants have a low probability of developing because the epidemic burns out. The observed times of emergence of the four VOCs fall well within the pattern of order-2 emergence times. However, emergence of the variant of interest D614G was early compared with the average time of 217 days for order-1 variants in the model.

Fig. 3.

The probability distribution for the day of the first emergence for each of the higher-order variants within a two-year period. The figure shows the results of 10,000 runs of the simulations shown in Fig. 2b, for the same parameters. Note that the probability of emergence of an order-4 variant is low because the epidemic usually burns out first. The time of emergence of several important variants is indicated with an arrow (D614G: February 2020; Alpha (α) 9/2020; Beta (β) 9/2020; Gamma (γ) 12/2020; Delta (δ) 12/2020).

3. Discussion

Since SARS-CoV-2 is constantly evolving, as evidenced by the continuing emergence of novel variants, the future dynamics of the pandemic remain uncertain. This uncertainty is accentuated by the increasing but unevenly distributed vaccination coverage and by vaccination resistance. It is not clear how the virulence of SARS-CoV-2 will evolve. The prevailing dogma for most of the 20th century was that disease organisms would always evolve toward benign coexistence with their hosts [15]. This view dominated both the academic [16] and popular literature [17] and so it is often argued that SARS-CoV-2 will follow a trajectory of diminishing virulence. However, as argued by Ewald 2004 [15] and as shown by the variants of SARS-CoV-2, this need not be the case. From the original variant to the currently advancing Delta variant, there has not been any notable decline in the relative fatality rate. However, infectiousness has been increasing. For example, according to Ref. [18], the Alpha, Beta and Gamma variants are up to 50% more transmissible than the original (Wuhan), while the Delta variant may be twice as transmissible. Thus, through the course of the pandemic, a prevailing feature is the growth of transmission coefficient in the variants, as expected from our analysis. With the rise of the percentage of vaccinated humans, we expect the virus to shift its evolutionary preferences towards escape mutations. A major unanswered question is whether there is a limit in viral fitness [19].

The probability of a successful mutation, p, is crucial because it determines which of the possible outcomes (no change in the system, cascade effect or a few dominant variants) will happen. For a mutational cascade to develop, a probability greater than 10⁻³ per infected person is required. Such large values seem unlikely for SARS-CoV-2. A more likely outcome is that a single mutation increases the R ₀ but without developing into a cascade of increasing R ₀. This happens because there is enough time for the first variant to infect most of the susceptible population but not enough time for the faster strains to reach high numbers and spawn further successful new strains. The new strain D614G that went on to replace the original Wuhan variant globally was first identified in February 2020 [20], when the total cumulative number of infected individuals was below 100,000; this would be consistent with a value of p > 10⁻⁵, i.e., the value that we used.

The COVID-19 pandemic represents an inadvertent experiment involving viral infection and mutation. Similar dynamics would not have been seen in other pandemics either because their expansion happened prior to the age of scientific observation or because they have been limited in their expansion (SARS-CoV-1). Interestingly, all the previously recognized RNA viral epidemic diseases with higher R ₀ concern viruses with smaller genomes than SARS-CoV-2. As SARS-CoV-2 has been established in the human population, in contrast to SARS-CoV-1 and MERS, the question then arises whether the accumulation of mutations associated with its larger genome might confer a greater potential for infectiousness compared to previous RNA viral diseases. Selection on the basis of growth rate alone can happen in the expansion phase of any invasive organism; this type of selection may be very different to that in an established population. For example, in the expansion of the cane toad (Rhinella marina), individuals tend to have longer legs on the invasion front [21], but once the population is established, short legs return [22]. Likewise, once the “frontier” closes for SARS-CoV-2, its evolution may join the more familiar pattern in other epidemics, optimizing for long-term coexistence with its hosts.

Hyper-exponential growth, which can be understood as an accelerating exponential curve, is of interest for a number of reasons. In addition to the current concern, HEG does not arise in most biological systems but in systems involving some sort of innovation and adaptation [23]. In contrast to exponential-type processes, such explosions reach a population singularity in finite time [11,23]. This model follows, as a single pair of differential equations, from the modified SEIR or related SIR (Susceptible, Infected, Removed) system, if mutation is included.

Our model is by necessity a simple one. We have not included spatial effects in it, nor the effects of age structure in the human population. These are factors that need to be incorporated when considering the worrying possibilities of uneven lockdown or non-homogenous vaccine coverage that might allow intense localized viral circulation. Our model of evolution is simplified and linear: while we consider different values for mutation probability, in any simulation, the probability of successful mutation (per infected person) is constant. We have assumed that mutations of viral traits are all independent, although, in reality, they may include trade-offs. We further have not considered the potential future effects of non-linear, epistatic mutations, as well as the effect of multiple sequential nucleotide mutations. In presenting our model, we have focused on the basic patterns we are likely to see when successful mutations arise in an expanding pandemic.

Following the emergence of D614G from the original Wuhan variant in February, the arrival of the three VOCs that emerged in late 2020 may be seen as the evolution of order-2 variants from an order-1 variant. Assuming there is no maximal viral advantage embodied in that configuration, our model predicts the timing of emergence of even more problematic higher-order variants (Fig. 3). This does not take into account the increased infectiousness of Delta variant, which also seems to be order-2, since Delta essentially appeared in late 2020 but was slower in its eventual successful introduction and dominance. In all runs of this model, large numbers of new strains emerged. The probability that the events will unfold similarly to Fig. 2b is hard to predict because these depend on factors not included in the model, such as spatial configuration and human responses. Our findings underline the need to minimize inhomogeneous vaccine coverage, since failure to do so along with other factors, like “social distancing fatigue” [14] and vaccination resistance, could contribute to pandemic resurgence and the possibility of HEG developing.

4. Materials and methods

Several authors have modeled the current pandemic in various places by a system of SEIR equations [13,14]. We use this model without age or spatial structure. We assume individuals who get infected spend on average D’ = 5.2 days in an asymptomatic pre-infectious phase and then D = 14 days upon becoming infectious before death or recovery [13,14], although the actual infectious period may be far shorter. In 2020, the global pandemic increased from a weekly average of 26 cases day⁻¹ (20th January) to one of 579,000 day⁻¹ (5th December), equivalent to an exponential growth rate of 0.031 day⁻¹, which we take as the basic growth rate. With each new infection, there is a fixed probability of a mutation causing a significantly higher growth rate (Fig. 2a). Such successful mutations happen according to a Poisson process, with fixed rate per infected person. We assume that this enters through the transmission parameter β in the equations, so that only the growth rate is affected. A virus with a transmission parameter β ₀ evolves into one with a parameter β ₀+Δβ and an associated reproductive number R ₀ ⁽¹⁾ (order-1). Further successful mutations (order-2, order-3, etc.), with transmission rates β ₀+2Δβ, β ₀+3Δβ, and so on, lead to still higher reproductive numbers R ₀ ⁽²⁾, R ₀ ⁽³⁾ …, respectively. This is typical for RNA viruses that are causative agents of major diseases throughout human history and which are transmitted via respiratory droplets or aerosols, including the measles virus with a R ₀ about 12–18, mumps (R ₀ ≈ 10–12) and rubella (R ₀ ≈ 6–7) [24]. We assume a limit for R ₀ to be 20, close to the highest known R ₀ (measles) for such viruses. We can associate these additive increments with successively adapting traits (spike protein, infectious period [25], heat resistance, etc). Our model follows each new strain that emerges from a significant mutation. We ignore strains that mutate to the same or lower R ₀, we do not include in the model complex mutations like blooms or super-spreader variants, and we do not make specific provisions for immuno-compromised populations that may harbor viral persistence, potentially initiating a novel variant.

In order to obtain results from our model, via simulation, we set up a series of difference equations to approximate the differential equations and solved it recursively, using the Euler method, for each time-step, following the standard approach [13,14]. Model time covers two years beginning with the start of the pandemic. We used the parameters above. In simulations, we kept track of all state variables for each of the strains created representing populations of cases for each of the strains in the pandemic. The only random element is the time of emergence of each new mutation. All calculations were performed in R [26].

4.1. Simulation model: the SEIR with evolving transmission rate

We begin with the standard SEIR model for a single strain [24] that contains equations for the number of susceptible people (S), the infected hosts (I ₀) and the number recovered or dead (R), plus an equation for the number of pre-infectious people (E ₀), so we have:

$$\begin{array}{l}\frac{dS}{dt}=-\beta SI\\ \frac{d{E}_0}{dt}=+\beta S{I}_0-f{E}_0\\ \frac{d{I}_0}{dt}=+f{E}_0-\gamma I_0\\ \frac{dR}{dt}=+\gamma I_0\end{array}$$ (1)

Here, f=1/D′, where D′ is the latency period, β is the per capita transmission rate and γ is the recovery rate. In Eq. (1), the infected stages have a subscript ‘0’ because they refer to the original strain. There may be several strains but the susceptible and recovered/removed sub-populations are common to all strains.

In our model, each subsequent strain, k, has its own subpopulation of pre-infectious and infectious individuals (E _k and I _k, respectively). Thus, if the total number of strains is K+1, we have K+1 pre-infectious {E ₀, E ₁, E ₂, …, E _K} and K+1 infectious {I ₀, I ₁, I ₂, …, I _K} subpopulations. Thus, we now have 2K + 4 equations in the system:

$$\begin{array}{l}\frac{dS}{dt}=-S\sum _{k=0}^K{\beta }_k{I}_k\\ \frac{d{E}_k}{dt}=+S{\beta }_k{I}_k-f{E}_k+{\delta }_k\text{for}k=\mathrm{0,1,2},\mathrm{....},K\\ \frac{d{I}_k}{dt}=+f{E}_k-\gamma I_k\text{for}k=\mathrm{0,1,2},\mathrm{....},K\\ \frac{dR}{dt}=+\gamma \sum _{k=0}^K{I}_k\end{array}$$ (2)

We assume that the latency time and the recovery rate are the same for all K+1 variants, but the transmission coefficient is assumed to change for each strain. This system of equations is solved by the Euler method using a time step of Δt.

The term δ _k is a random variable associated with the creation of strain k from strain k-1. For a system with strains 0,1,2, …,k-1 already in circulation, the creation of the new strain “k” proceeds as follows: For each host-pathogen interaction, we assume a probability p of a successful mutation establishing a new strain. There are β _k-1 I _k-1(t)S(t)Δt such interactions in the time step of length Δt, based on Eq. (1). Thus, for a successful new mutation (one for which the infectiousness is at least as high), the probability of emergence is p _k = pβ _k-1 I _k-1(t)S(t)Δt (for all k > 0). In the simulations, the creation of a new strain is thus decided by the random variable δ _k, which is unity with probability p _k and zero with probability 1-p _k. If δ _k = 1, the new strain is created and the population of E _k jumps from zero to unity in the time interval [t, t+Δt] so that E _k(t+Δt) = 1. Then, the new strain has a transmission coefficient of

$${\beta }_{K+1}={\beta }_K+\Delta \beta$$ (3)

Suppose Δβ = 0.9β ₀ and four variants existing, variant-0 with transmission coefficient β ₀ and three others, variant-1, variant-2 and variant-3, each with transmission coefficient 1.9β ₀. If a mutation happens in variant-0, the result is the creation of a new strain, variant-4, again with 1.9β ₀. If, however, the mutation happens in one of the other strains, we have a new strain with transmission coefficient β ₄ = 2.8β ₀.

We assume that an important mutation, one that increases transmission rate by at least Δβ, has a probability p, which is typically very small for an individual. For such a mutation to happen somewhere in the population, when R individuals have had the disease after a time Δt ₁, then pR should have reached at least unity. R is found by integrating Eq. (1d) for a variant that initially grows exponentially from a single infection:

$$R\left(t_1\right)=\gamma \underset{0}{\overset{t_1}{\int }}I\left(t\right)dt\approx \frac{e^{\lambda t_1}}{\lambda D}=\frac{I\left(t_1\right)}{\lambda D}$$ (4)

Using the requirement that R(t ₁)≈1/p, we can invert this to get the time-interval for the appearance of the new variant,

$$t_1\approx \frac{1}{\lambda }\ln \left[D\lambda /p\right]$$ (5)

Thus, if D = 14 days, and we assume a doubling time of 3 weeks (λ = 0.031), using these numbers in Eq. (5), we get the first successful mutation appearing after t ₁ = 270 days if p = 10⁻⁴, or after t ₁ = 493 days if p = 10⁻⁷. Subsequent variants of the same order will occur more quickly because of the higher abundance, given the exponential growth (see Fig. 2b). However, the time for these new strains to reach sufficient abundance and start generating their own mutations may be substantial. For achieving parity with an exponentially growing variant of initial abundance I ₀, the new mutant with Δλ greater growth rate still needs time:

$$t_2=\frac{\ln (I\left(t_1\right))}{\Delta \lambda }$$ (6)

For example, the D614G variant, appearing around 20^th February 2020 (very early, according to Eq. (5)), took three months to attain dominance over the D614C form [20]. If we use a figure of 52,000 (the sum of new cases over the previous 14 days) as an estimate of the number of infected people I(t ₁), then a difference of Δλ = 0.12 per day would bring about parity within 90 days.

4.2. The differential equations of hyper-exponential growth

The SIR equations, based on a simpler model that assumes that the latency period is small, may be written as follows [27]:

$$\begin{array}{l}\frac{dI}{dt}=-\beta SI\\ \frac{dI}{dt}=+\beta SI-\gamma I\\ \frac{dR}{dt}=+\gamma I\end{array}$$ (7)

In the earliest stages of the epidemic, the number of infections is small relative to the total population, so S ≈ N. We can then solve Eq. (7b) by solving the equation dI/dt≈(βN−γ)Ι ≈ λI. Since λ is constant, the solution of this is exponential growth with rate λ. Note that, in the SIR model, λ is related to the reproductive number by λ=(R ₀-1)γ.

We assume that the per capita transmission coefficient, β, can be altered by successful mutations. If these are plentiful, we assume that there is a large number of successful or neutral mutations independent of each other and each leading to the same increase in β, and, correspondingly, in growth rate, λ. We refer to the incremental increase in λ as Δλ. If the number of people who have had the disease is R, using Eq. (7c) and the fact that the probability of a successful mutation is p, then the change in the number of successful mutations is proportional to R, i.e. Δλ∝pΔR, so we can submit this into the third equation to get:

$$\begin{array}{l}\frac{dI}{dt}=\lambda \left(t\right)\cdot I\left(t\right)\\ \frac{d\lambda }{dt}=\rho \cdot I\left(t\right)\end{array}$$ (8)

where the constant ρ ∝ p/D.

Author contributions

John Halley: Conceptualization, Formal analysis, Visualization, Writing-Original draft preparation, Writing-Reviewing and Editing; Despoina Vokou: Investigation; Writing-Reviewing and Editing; Georgios Pappas: Investigation, Visualization, Writing-Original draft preparation, Writing-Reviewing and Editing; Ioannis Sainis: Investigation, Writing-Reviewing and Editing

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following are the Supplementary data to this article: