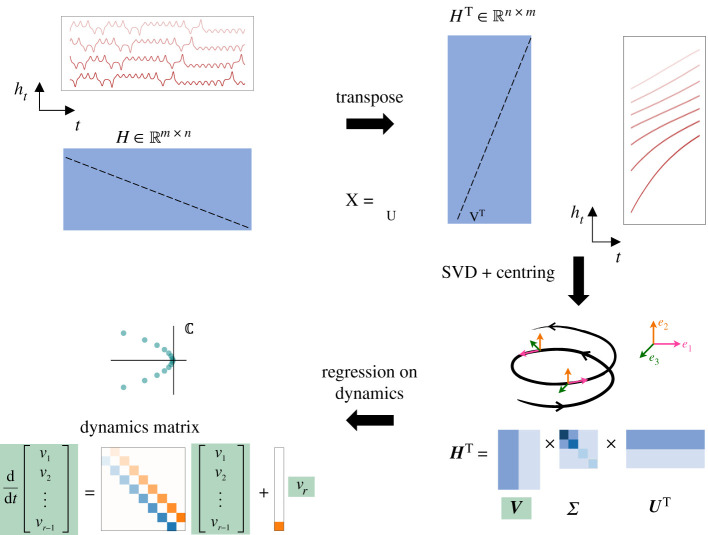
Figure 3.

An illustration of how a highly structured, antisymmetric linear model arises from time-delay data. Starting with a one-dimensional time series, we construct a $m\times n$ Hankel matrix using time-shifted copies of the data. Assume that $n\gg m$, in which case $\mathit{H}$ can be thought of as an $m$ dimensional trajectory over a long period ($n$ snapshots in time). Similarly, the transpose of $\mathit{H}$ may be thought of as a high dimensional ($n$ dimensional) trajectory over a short period ($m$ snapshots) in time. With this interpretation, by the results of [33], the singular vectors of $\mathit{H}$ after applying centring yield the Frenet–Serret frame. Regression on the dynamics in the Frenet–Serret frame yields the tridiagonal antisymmetric linear model with an additional forcing term, which is non-zero only in the last component.