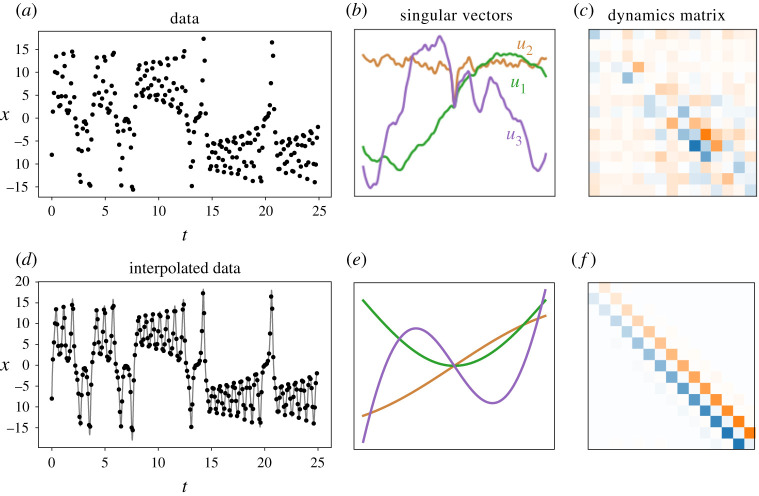
Figure 6.

In the case where a dynamical system is sparsely sampled, interpolation can be used to recover a more tridiagonal and antisymmetric matrix for the linear model in HAVOK. First, we simulate the Lorenz system, measuring $x(t)$ with a sampling period of $\mathrm{\Delta }t=0.1$. The resulting dynamics model $\mathit{A}$ and corresponding singular vectors of $\mathit{U}$ are plotted. Due to the low sampling frequency, these values do not satisfy the requirements in (4.1). Consequently, the dynamics matrix is not antisymmetric and the singular vectors do not correspond to the orthogonal polynomials in §3c. Next, the data are interpolated using cubic splines and subsequently sampled using a sampling period of $\mathrm{\Delta }t=0.001$. In this case, the data satisfy the assumptions in (4.1), which yields the tridiagonal antisymmetric structure for $\mathit{A}$ and orthogonal polynomials for $\mathit{U}$ as predicted. (Online versionin colour.)