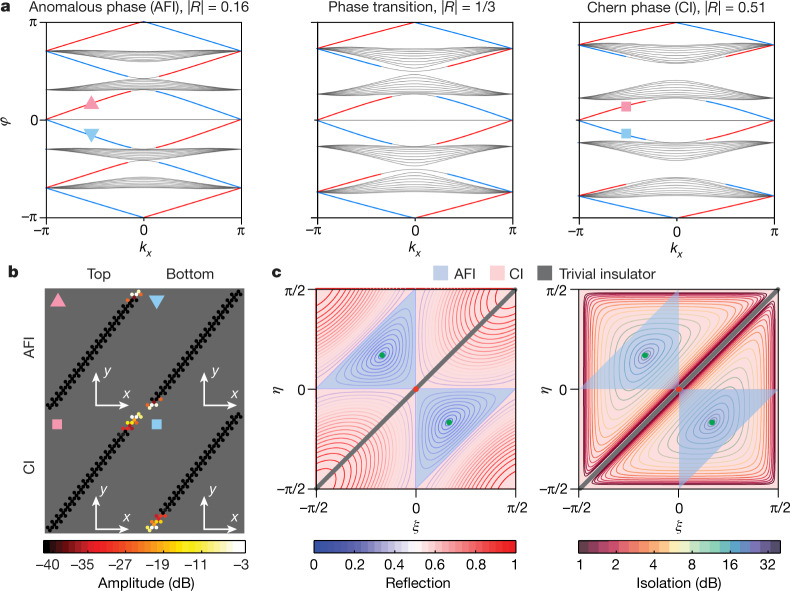
Fig. 2. Anomalous and Chern topological phases in non-reciprocal wave networks.

a, Band structure of a supercell with periodic boundary conditions along x and unitary reflection at the top and bottom. The parameters are the same as in Fig. 1c. The low-reflection case is the anomalous topological phase (an anomalous Floquet insulator, AFI), which features an edge mode in every quasi-energy gap. Conversely, the high-reflection case supports edge modes only inside the type 1 bandgaps, consistent with the Chern insulator (CI) phase. Edge modes localized to the top and bottom are shown in red and blue, respectively. The phase transition is depicted in the middle panel. b, Supercell with examples of the profiles of Chern and anomalous topological edge modes, corresponding to the markers in a. c, Topological phase diagrams in the (ξ, η) plane. The blue-shaded areas correspond to the anomalous phase, and the red-shaded areas to the Chern phase. Left, comparison with the iso-reflection contours of the individual scatterers, demonstrating the coincidence between the topological phase transition and the |R| = 1/3 contour. Right, comparison with the non-reciprocal isolation level of the individual scatterers |S₂₁/S₁₂|. On the thick grey diagonals in panel c, the scatterers are reciprocal and the type 1 bandgaps close. At the centre red point, all bandgaps close. The two green points represents the perfect circulator cases, either with right-handed circulation (upper-left point) or left-handed circulation (lower-right point).