Bubble Cloud Behavior and Ablation Capacity for Histotripsy Generated from Intrinsic or Artificial Cavitation Nuclei

Abstract

This study examines the effects of cavitation nuclei characteristics on histotripsy. High-speed optical imaging was used to compare bubble cloud behavior and ablation capacity for histotripsy generated from intrinsic and artificial cavitation nuclei (gas-filled microbubbles, fluid-filled nanocones). Results showed a significant decrease in the cavitation threshold for microbubbles and nanocones compared to intrinsic nuclei controls, with predictable and well-defined bubble clouds generated in all cases. Red blood cell experiments showed complete ablations for intrinsic and nanocone phantoms, but only partial ablation in microbubble phantoms. Results also showed a lower rate of ablation in artificial nuclei phantoms due to reduced bubble expansion (and corresponding decreases in stress and strain). Overall, this study demonstrates the potential of using artificial nuclei to reduce the histotripsy cavitation threshold while highlighting differences in the bubble cloud behavior and ablation capacity that need to be considered in the future development of these approaches.

Introduction

Histotripsy is a focused ultrasound therapy currently being developed for non-invasive tissue ablation. Unlike thermal High-Intensity Focused Ultrasound (HIFU) that ablates targeted tissue via thermal necrosis (Elhelf, et al. 2018), histotripsy is a form of a non-thermal ablation that uses precisely controlled acoustic cavitation to produce the mechanical disintegration of target tissues (Xu, et al. 2004, Parsons, et al. 2006a, Bader, et al. 2019). Histotripsy is typically generated using high pressure (>10 MPa) and short duration (<20 μs) focused ultrasound pulses applied at very low duty cycles (<1%) to generate a characteristic cavitation “bubble cloud” at the focus (Xu, et al. 2004, Xu, et al. 2007, Maxwell, et al. 2013, Vlaisavljevich, et al. 2014b). Cavitation bubble clouds induce high stress and strain in the target tissue at the subcellular level, resulting in complete tissue disintegration into an acellular homogenate with no remaining cellular structures (Vlaisavljevich, et al. 2013b, Vlaisavljevich, et al. 2016c). Due to these features, histotripsy is being developed as a potential non-invasive ablation method for multiple applications including the treatment of benign prostatic hyperplasia (Hempel, et al. 2011, Roberts, et al. 2014, Schuster, et al. 2018), thrombus obstruction (Maxwell, et al. 2011a, Bader, et al. 2016, Gerhardson, et al. 2017, Zhang, et al. 2017) , and cancer (Styn, et al. 2010, Vlaisavljevich, et al. 2013b, Smolock, et al. 2018, Worlikar, et al. 2018, Longo, et al. 2019, Qu, et al. 2020).

Prior work studying histotripsy has shown that cavitation bubble clouds can be generated from multi-cycle pulses (shock scattering histotripsy, boiling histotripsy) (Maxwell, et al. 2011b, Vlaisavljevich, et al. 2014b, Khokhlova, et al. 2017, Maxwell, et al. 2017) or from 1–2 cycle pulses with a single tensile phase (intrinsic threshold histotripsy) (Maxwell, et al. 2013, Vlaisavljevich, et al. 2015b, Vlaisavljevich, et al. 2017). In intrinsic threshold histotripsy, bubble clouds are generated from de novo cavitation nuclei that are intrinsic to the medium (i.e. nuclei that are intrinsic to the water inside the tissue) when the tissue is exposed to histotripsy pulses with a single dominant negative pressure phase (Maxwell, et al. 2013, Lin, et al. 2014, Vlaisavljevich, et al. 2015b). Cavitation initiation depends on the amplitude and duration of the applied negative pressure (p-) as well as the properties of the media, with the intrinsic threshold measured to be ~25–30 MPa for water-based soft tissues when tested at ultrasound frequencies ranging from 345 kHz to 3 MHz (Maxwell, et al. 2013, Lin, et al. 2014, Vlaisavljevich, et al. 2015b). Using this approach, intrinsic threshold histotripsy results in characteristic “Microtripsy” bubble clouds that are capable of generating well-defined ablation zones that precisely and predictably match the region of the beam profile above the intrinsic threshold (Maxwell, et al. 2013, Lin, et al. 2014, Vlaisavljevich, et al. 2017). Prior work has suggested that the high reliability, high accuracy, ability to treat near interfaces without pre-focal cavitation, and ability to manipulate bubble behavior by changing transducer and pulsing parameters make intrinsic threshold histotripsy the preferred treatment modality for most applications in which sufficiently high negative pressures can be achieved (Maxwell, et al. 2013, Lin, et al. 2014, Vlaisavljevich, et al. 2015c, Vlaisavljevich, et al. 2017).

In addition to conventional histotripsy, which generates bubble clouds directly from de novo cavitation nuclei that are intrinsic to the medium, it is also possible to utilize artificially introduced exogenous cavitation nuclei to reduce the cavitation threshold for histotripsy. For instance, gas-filled microbubbles (MBs, ~1–10 μm) have long been used to artificially lower the cavitation threshold and enhance cavitation activity (Hynynen, et al. 2003, Tran, et al. 2003, Mcdannold, et al. 2006, Bader, et al. 2016). More recently, nanoparticle-mediated histotripsy (NMH) has been developed as a targeted ablation method that combines fluid-filled nanoparticles with histotripsy pulsing modalities (Vlaisavljevich, et al. 2013a, Yuksel Durmaz, et al. 2014, Aydin, et al. 2016, Khirallah, et al. 2019). Nanoparticles used in NMH can consist of perfluorocarbon (PFC) nanodroplets (NDs, ~200–400 nm) (Yuksel Durmaz, et al. 2014, Vlaisavljevich, et al. 2015a, Vlaisavljevich, et al. 2016a) or recently developed PFC nanocones (NCs, ~30–50 nm) (Rehman, et al. 2019). Unlike MBs, which lower the cavitation threshold by directly providing gas nuclei for seeding cavitation, NDs and NCs reduce the cavitation threshold for histotripsy due to the lower nucleation threshold of the PFC fluid inside the particles, matching the predictions of classical nucleation theory (CNT) (Arvengas, et al. 2011, Vlaisavljevich, et al. 2016b, Miles, et al. 2018). The smaller size of the nanoparticles allows for penetration through the tumor vasculature, potentially enabling the targeted ablation of a wide range of cancerous tissues commonly targeted with histotripsy. Although the clinical applications for microbubble-mediated histotripsy (MMH) are more limited due to tissue penetration, recent work has demonstrated the improved contrast imaging of cancerous tumors through selective accumulation of cationic MBs in the tumor vasculature (Diakova, et al. 2020). In addition, other work has developed MBs for enhanced thrombolysis and targeted non-invasive surgery in which MBs are directly delivered into the tissue have shown the potential for applying histotripsy at significantly reduced pressures (Tran, et al. 2003, Bader, et al. 2016), with a potential advantage of MMH over NMH being the possible use of FDA approved ultrasound imaging contrast agents.

While these prior studies demonstrate the potential of improving histotripsy for certain clinical applications by using artificial cavitation nuclei to reduce the histotripsy cavitation threshold, the bubble cloud dynamics and ablation produced under these particle-mediated histotripsy conditions have not been thoroughly compared. It remains an open question whether or not histotripsy bubble clouds generated from artificial cavitation nuclei can replicate the characteristic predictable and well-defined Microtripsy bubble clouds. Furthermore, recent studies suggest that histotripsy bubbles generated from exogenous nuclei will be less efficient at ablating tissue due to a reduced maximum radius (R_max) for bubbles generated at the lower applied pressures, which corresponds to a decrease in the stress and strain exerted on the tissue (Vlaisavljevich, et al. 2013a, Vlaisavljevich, et al. 2015c, Bader and Holland 2016, Mancia, et al. 2017, Mancia, et al. 2019). This hypothesis appears to be supported by previous NMH studies that showed NMH achieved complete ablation of red blood cell (RBC) phantoms after ~2,000 pulses (Vlaisavljevich, et al. 2013a, Vlaisavljevich, et al. 2016a), which was significantly more pulses than what has previously been shown to ablate RBC phantoms in prior Microtripsy studies (Lin, et al. 2014, Vlaisavljevich, et al. 2017).

In this study, we investigated the bubble cloud behavior and ablation capacity of histotripsy generated from intrinsic and artificial cavitation nuclei using 1–2 cycle acoustic pulses typically used for generating Microtripsy bubble clouds. Experiments utilized high-speed optical imaging to characterize the histotripsy cavitation threshold, bubble cloud dimensions, cloud sustainability over multiple pulses, and ablation capacity in tissue phantoms containing decafluorobutane (DFB) gas-filled MBs, perfluorohexane (PFH) NCs, or control phantoms with no artificial nuclei (i.e. intrinsic threshold histotripsy). We hypothesized that both MBs and NCs would significantly reduce the histotripsy cavitation threshold compared to intrinsic threshold histotripsy, with a significantly lower threshold for phantoms containing MBs than for phantoms containing NCs. Furthermore, it was expected that the bubble clouds generated from NMH and intrinsic threshold histotripsy would demonstrate Microtripsy characteristics (i.e. predictable, well-defined bubble clouds matching the focal region above the respective cavitation thresholds). Finally, we hypothesized that the ablation efficiency would decrease for histotripsy bubble clouds generated from artificial nuclei compared to intrinsic threshold histotripsy due to reduced bubble expansion (expected for both MBs and NCs) and decreased cloud sustainability (expected for MBs only). Overall, the results of this study can provide insight into the histotripsy ablation process for particle-mediated histotripsy, which is essential to the development of these emerging ablation methods.

Materials and Methods

Histotripsy Pulse Generation and Experimental Set-Up

A thirty-two element 500 kHz array transducer with a geometric focus of 75 mm, an aperture size of 120.5 mm, and an f-number of 0.62 was used for all experiments in this study. The transducer was composed of three concentric circles of six, twelve, and fourteen elements, each with a 20 mm diameter. The transducer was driven via a custom high-voltage pulser designed to generate short therapy pulses of <2 cycles. The pulser was connected to a field-programmable gate array (FPGA) board (Altera DE0-Nano Terasic Technology, Dover, DE, USA) specifically programmed for histotripsy therapy pulsing. The transducer was fixed horizontally in a tank of degassed water, and a computer-guided 3D-positioning system was used to orient the tissue phantoms to the focus of the transducer in all experiments (Fig. 1A). MATLAB (The MathWorks, Natick, MA, USA) simultaneously controlled the positioning system and the transducer to ensure accurate positioning, pulsing, and hydrophone measurements.

Figure 1.

Histotripsy Experimental Schematic. High-speed optical imaging was used to capture cavitation behavior and red blood cell (RBC) ablation inside agarose tissue phantoms exposed to histotripsy pulses applied by a 500 kHz transducer.

Hydrophone Focal Pressure Calibration

Focal pressure waveforms for the 500 kHz transducer were measured with a custom-built fiber optic probe hydrophone (FOPH) (Parsons, et al. 2006b). The FOPH was cross-calibrated at low-pressure values with a high-sensitivity reference hydrophone (HNR-0500, Onda Corporation, Sunnyvale, CA, USA) to ensure accurate pressures were measured from the FOPH. The reference hydrophone was also used to measure the focal beam profile of the transducer, where the transverse and axial full width half maximum (FWHM) dimensions at a geometric focus of the transducer were measured to be 2.2 mm and 6.5 mm, respectively. The 1-D beam profiles in the lateral, elevational, and axial directions were measured by scanning the hydrophone over a range of 16 mm in the axial directions and 8 mm in the transverse and elevational directions with steps of 0.1 mm. The measured peak negative focal pressure from these scans was ~1.8 MPa. The acoustic pressures used for all experiments were measured by the FOPH in degassed water (~26% dissolved O₂) at the focal point of the transducer, which was identified using a 3-D beam scan. Focal pressures were directly measured with the FOPH up to a peak negative pressure (p-) of 20 MPa and estimated for higher pressure levels (p- > 20 MPa) by summating measurements from subsets of eight and sixteen elements. A Tektronix TBS2000 series oscilloscope measured all waveforms at a sample rate of 500MS/s, and the waveform data was averaged over 512 pulses and recorded in MATLAB. A sample acoustic waveform measured by the FOPH is shown in Figure 2 along with representative 1-D beam profiles from the 500 kHz transducer.

Figure 2.

Acoustic Waveform and Beam Profiles. A) Example 500 kHz histotripsy waveform measured by the FOPH along with the 1-D beam profiles in the B) axial and C) transverse directions measured by the HNR-0500 hydrophone.

Formulation of Gas-filled Microbubbles

Cationic lipid-shelled MBs (Fig. 3A) were synthesized following recently published methods (Gorick, et al. 2020). Briefly, a micellar aqueous mixture of 2 mg/ml 1,2- distearoyl-sn-glycero-3-phosphocholine (DSPC; Avanti Polar Lipids, Alabastar, Alabama), 2 mg/ml polyethylene glycol 6000 monostearate (PEG 6000 MS; Stepan Kessco, Northfield, Illinois), and 0.8 mg/ml 1,2-distearoyl-3-trimethylammonium-propane (DSTAP; Avanti Polar Lipids, Alabastar, Alabama) in 0.9% NaCl (Baxter, Deerfield, Illinois) was prepared by probe-type sonication (20 kHz, 3 min, 50% power, XL2020 instrument, Misonix Inc., Farmingdale, New York). The sonicated medium was filtered through a 0.2 μm Nylon sterile filter, sparged with decafluorobutane gas (DFB, F2 Chemicals Ltd; Preston, United Kingdom), and then sonicated at the highest power (20 kHz, 30 s) with the same sonicator to generate the MBs. The average mean and median diameters of the microbubbles for all samples were between 1.5–2.5 μm with >95.5% of MBs having a diameter less than 5 μm as measured by Coulter Multisizer 3 (Beckman Coulter, Inc., Hialeah, FL) with a 50 μm orifice. MBs were then aliquoted into 13 mm glass vials, which were stoppered for refrigerated storage after filling the headspace with DFB gas. MBs were counted prior to each set of experiments, with the concentration of the vials confirmed using an auto cell counter (TC10™, Bio-Rad Laboratories, Inc., Hercules, CA, USA).

Figure 3.

Microbubble and Nanocone Schematics. Artistic renderings of the (A) gas-filled microbubbles and (B) fluid-filled nanocones that were used as artificial nuclei in this study.

Formulation of PFH Nanocones

PFH-NCs (Fig. 3B) were prepared via host-guest interaction between β-cyclodextrin (BCD) and PFH with an optimized method similar to the recently published work (Rehman, et al. 2019). Briefly, BCD (100 mg, 8.8 × 10⁻² mmol) was completely dissolved in double-distilled water (6 mL) at room temperature followed by the addition of PFH at the optimized molar ratio of 1:5 (BCD:PFH). After overnight stirring, precipitates, which are the NC aggregates that include the inclusion complex of PFH and BCD as building blocks, can be separated by simple filtration or centrifugation and then dried in vacuum to get solid white powder. The PFH content of the obtained powder was calculated using Gas Chromatography through a calibration curve containing different concentrations of free PFH. Further evidence for the presence of the PFH was confirmed using SEM-EDAX analysis.

Agarose Phantom Preparation

Tissue phantoms containing 1% (w/v) agarose were used in this study to provide a viscoelastic medium replicating the mechanical and viscoelastic properties of soft human tissue. Prior studies have shown the Young’s modulus of 1% (w/v) agarose to be 21.7 kPa, which is within the range of ~6–25 kPa that characterizes liver, kidney, muscle, and other relevant tissues that are principle targets for histotripsy (Vlaisavljevich, et al. 2015c). The gel was made by mixing 0.5 % agarose powder (Type VII-A, Sigma Aldrich Corporation, St. Louis, MO, USA) with 99.5% of a 0.45% saline solution at room temperature. The mixture was heated in a microwave until boiling and then stirred to ensure the agarose was fully dissolved. Next, the sample was repeatedly heated to boiling and stirred to produce flash boiling to release dissolved gas from the mixture until it was fully degassed and 50% of the volume remained to obtain a degassed 1% (w/v) agarose with 0.9% saline content gel mixture. The mixture was placed under a partial vacuum (~33.62 kPa, absolute) for 30 minutes to remove the remaining gas at a low boil and minimize re-gassing as the agarose solution cooled. For the final 5 minutes, the pressure was decreased to ~16.75 kPa to force any remaining gas from solution. Once the temperature of the agarose dropped to 40°C, a serological pipette was used to inject 50 mL of the gel into a custom-designed PLA frame inside a rectangular silicone mold. The agarose gel was slowly pipetted down the wall of the silicone mold onto the phantom holder frame to avoiding introducing any gas during the process. The silicone mold containing the gel was then stored in a refrigerator for one hour to solidify. Each test was performed within two hours of the gel creation to ensure the agarose concentration and degassed state of the gel remained consistent during testing.

The agarose phantoms with embedded NCs were prepared by first combining desiccated NC powders with 10 mL of degassed saline, forming a solution with an NC concentration of 10⁻³ mL PFH/mL water. The degassed saline and NC solution was then stirred at 600 rpm for 30 min to allow all of the NC particles to become well-dispersed in the solution. Once the temperature of the degassing agarose was <38°C, 0.5 mL of NCs in degassed saline were added by a 1 mL syringe to the 1% agarose gel phantom and incorporated by gentle stirring with a glass stir rod. The resulting agarose became a 1% (w/v) phantom containing NCs with a final concentration of 10⁻⁵ mL PFH/mL water, matching prior work showing this concentration generated desirable cavitation results (Khirallah, et al. 2019). The phantom holders were placed in a refrigerator to allow the solution to solidify, forming tissue phantoms with embedded NCs. For agarose phantoms with embedded MBs, a 4 mL gasket-sealed vial of MBs was first removed from the 4°C refrigerator, and the MB were resuspended by manual gentle inversion. A 1 mL syringe with a 25-gauge needle was used to remove 0.1 mL of the MB solution from the sealed vial which was combined with 0.9 mL of 0.9% saline in a small beaker. Before use, MB concentration was confirmed using an auto cell counter (TC10™, Bio-Rad Laboratories, Inc., Hercules, CA, USA). Once the 1% agarose mixture had cooled to ~38°C, a 1 mL syringe with a 25-gauge needle was used to remove a small volume (<2mL) containing 10⁷ or 10⁸ microbubbles. The MBs volume was added to the agarose solution and stirred by the syringe to produce a 1% agarose gel with a microbubble concentration of 10⁵ (multi-pulse sustainability and red blood cell ablation testing) or 10⁶ MBs/mL (cavitation threshold and bubble cloud dimensions testing), which is within the range of concentrations seen in prior work proposing MBs for enhanced surgery and thrombolysis (Tran, et al. 2003, Bader, et al. 2016). The holders were placed in a refrigerator to allow the solution to solidify, forming tissue phantoms with embedded MBs. It should be noted that the reported MB concentrations were measured prior to gel formation, and small changes in the final concentration could be possible due to the gel polymerization processes during refrigeration.

For ablation experiments, red blood cell (RBC) phantoms were created consisting of three layers of agarose, with the middle layer containing 5% (v/v) red blood cells (Maxwell, et al. 2010, Vlaisavljevich, et al. 2013a). Fresh porcine blood was obtained from subjects in an unrelated study and added to an anticoagulant solution of Citrate Phosphate Dextrose Anticoagulant (CPD, Sigma Aldrich Corporation, St. Louis, MO, USA), with a CPD-to-blood ratio of 1:9 mL. Whole blood was separated by centrifugation at 3,000 rpm for 10 min. The plasma and white buffy coat were removed, and the RBCs were saved for addition to the phantom. The RBC phantom was created using an initial layer of 1% agarose mixture (containing artificial or intrinsic nuclei) that was poured into the tissue phantoms holders at 40°C. The housing was placed in a refrigerator at 4°C to allow the agarose to cool and solidify. For our intrinsic control phantoms, the remaining solution was kept at 38°C. For MB and NC phantoms, a second solution of agarose was produced and lowered to <38°C before the respective nuclei were added. 9.5 mL of the respective agarose solutions were combined with the RBCs (5% v/v) by gentle inversion and poured on top of the chilled solidified agarose layer in the phantom. The liquid RBC-agarose solution was poured into the set agarose layer and allowed to coat the entire surface before the excess solution was poured out leaving behind a thin layer of the RBC-agarose solution and the whole phantom placed in the refrigerator. After 5 minutes, the RBC-agarose layer was solidified, and the remaining agarose solution without RBCs was poured to fill the frame. This procedure created a thin layer of RBCs suspended in the center of the agarose phantom (Fig. 1C).

Cavitation Detection using Optical Imaging

High-speed optical imaging was used to capture images of the focal zone after propagation of each pulse (Fig. 1A). Optical imaging was performed using a high-speed camera (FLIR Blackfly S monochrome, BFS-U3–32S4M-C 3.2 MP, 118 FPS, Sony IMX252, Mono, FLIR Integrated Imaging Solutions, Richmond, BC, Canada) and a 100 mm F2.8 Macro lens (Tokina AT-X Pro, Kenko Tokina Co., LTD, Tokyo, Japan). This setup resulted in captured images with a resolution of 3.25 μm per pixel, with the camera triggered to record one image for each applied pulse during cavitation experiments and two images for each pulse for RBC ablation experiments. The tissue phantom was backlit by a custom-built pulsed white-light LED strobe light capable of high-speed triggering with 1 μs exposures. Strobe duration was kept as low as possible (3–5 μs) to ensure minimal motion blur of the expanding bubbles. All exposures were centered at a delay of 8.5 μs after the pulse reached the focus as this was determined to be the optimum delay for visualizing the complete bubble clouds at a time point before substantial bubble coalescence or overlap of the expanding bubbles. A program using image processing software (MATLAB, The MathWorks, Natick, MA, USA) was created to perform the analysis on each image collected. The acquired images were converted from grayscale to binary by an intensity threshold determined by the background intensity as described in a previous study (Maxwell, et al. 2013). Bubbles were indicated by any black regions >5 pixels. By this criterion, the minimum resolvable bubble diameter was ~16 μm.

Cavitation Threshold Calculation and Comparison

For cavitation threshold experiments, 100 pulses were applied at a range of p- levels to a single point inside MB, NC, and intrinsic nuclei tissue phantoms submerged inside a water tank (Fig. 1A). Pulses were applied to the tissue phantoms at a pulse repetition frequency (PRF) of 0.5 Hz to minimize the possibility that cavitation from one pulse would change the probability of cavitation on a subsequent pulse (e.g. sufficient time between pulses allows for bubbles to dissolve before the subsequent pulse arrives) (Maxwell, et al. 2013, Vlaisavljevich, et al. 2015a). For each experimental condition, experiments were conducted at incremental p- levels ranging from 0.15 MPa to a maximum p- of 45 MPa. This pressure range was chosen to cover the full range of pressures needed to calculate the cavitation threshold and compare the bubble cloud behavior for all experimental conditions. For each pulse, cavitation was monitored using high-speed imaging, as described in the previous section, and the fraction of total pulses (out of 100) for which cavitation was detected was determined as the cavitation probability, p_cav, for each pressure level tested.

The resulting images were used to calculate the cavitation threshold for each experimental condition using a method described previously (Maxwell, et al. 2013, Vlaisavljevich, et al. 2015b). For each experimental condition, the probability of observing cavitation followed a sigmoid function, given by

$$P\left(p_{\_}\right)=\frac{1}{2}+erf\left(\frac{p\_-p_t}{\sqrt{2{\sigma }^2}}\right)$$ (E1)

where erf is the error function, p_t is the negative pressure at which the probability p_cav=0.5, σ is a variable related to the width of the transition between p_cav=0 and p_cav=1, with ± σ giving the difference in pressure from about p_cav=0.15 to p_cav=0.85 for the fit (Maxwell, et al. 2013). The cavitation threshold for each sample, p_t, is defined as the p- corresponding to p_cav=0.5 as calculated by the curve fit. Curve fitting for all data sets was performed using MATLAB software. The cavitation thresholds for MB, NC, and control phantoms were determined as p-_MB, p-_NC, and p-_HIT, respectively.

Bubble Cloud Dimensions: Prediction vs. Measurement

The predicted bubble cloud dimensions for each experimental condition were estimated following a previously published method (Lin, et al. 2014, Vlaisavljevich, et al. 2017) to determine if predictable and reproducible bubble clouds could be generated from both artificial and intrinsic cavitation nuclei. Cloud dimensions were estimated using the 1-D beam profiles measured in the transverse, elevational, and axial directions of the transducer (Fig. 2B/C). The 1-D beam profiles were normalized to the p- at the focus for each pressure level tested experimentally, and an estimated beam profile was obtained by multiplying the normalized 1-D beam profiles with each specific p-. The predicted bubble cloud dimensions were estimated by measuring the region of the beam profiles above the experimentally measured cavitation thresholds for MB (p-_MB), NC (p-_NC), and histotripsy intrinsic threshold (p-_HIT) conditions (Fig. 4). The predicted bubble cloud size was calculated in the axial and lateral directions for all experimental conditions and compared to the cloud dimensions measured experimentally using optical imaging, as shown in Figure 4. A sample size of 100 bubble clouds was used to measure the cloud dimensions at each pressure level for each set of experimental conditions, with the results reported as the average ± the standard deviation. Measured bubble cloud dimensions within 20% of the predicted cloud measurements were considered to be in close agreement.

Figure 4.

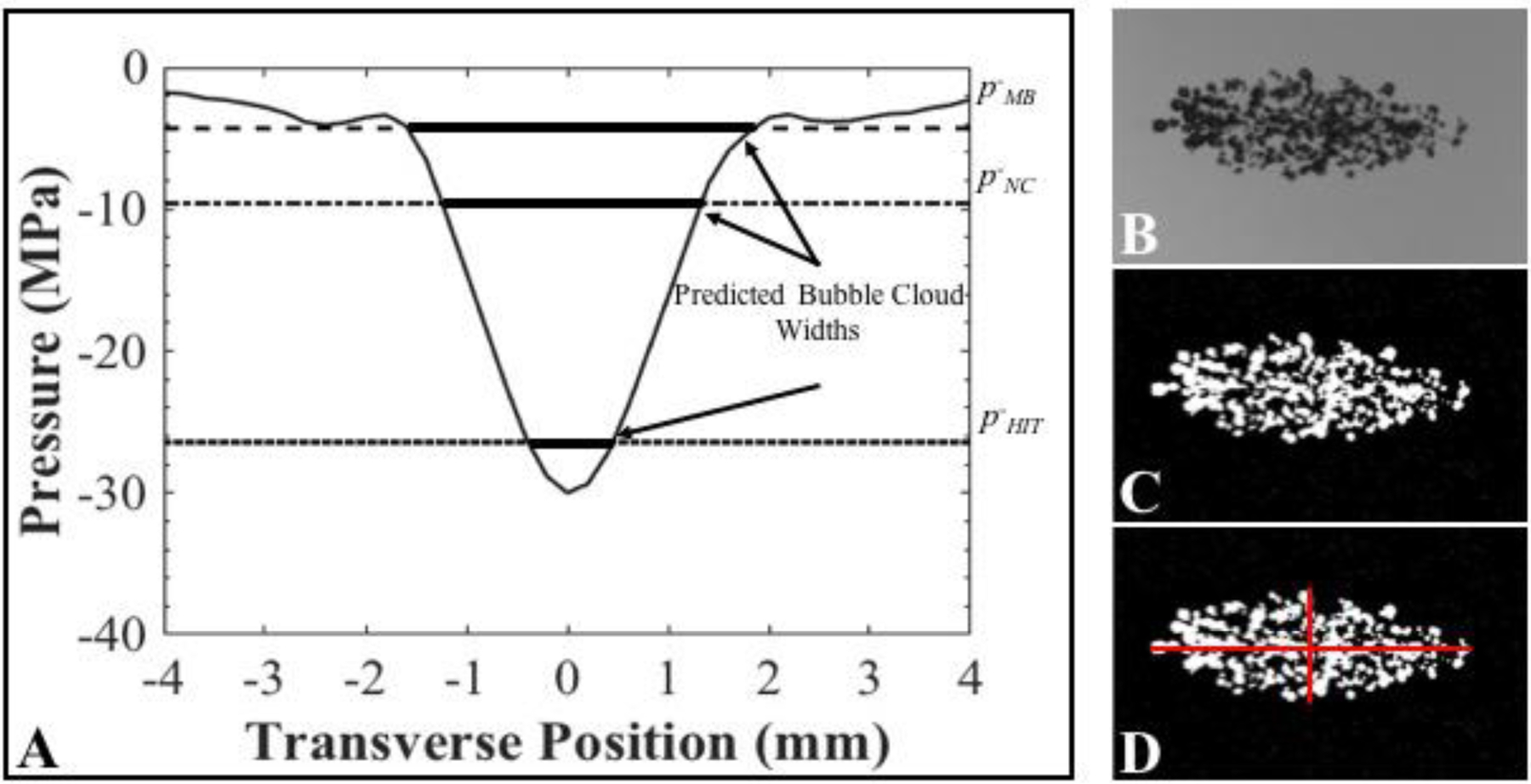
Bubble Cloud Size: Predicted vs. Measured Methods. (A) Scaled 1-D beam profiles were used to predict the bubble cloud dimensions (plot shows example profile scaled to p- = 30 MPa). Optical images were processed to measure the bubble cloud dimensions. Images show original cloud image (B), converted binary image (C) and dimensional measurements (D). Results were compared to predicted cloud widths.

Multi-pulse Sustainability

The sustainability of cavitation over the course of multiple pulses was investigated in agarose tissue phantoms containing MBs, NCs, and control phantoms (intrinsic nuclei). 2,000 histotripsy pulses were applied to a single focal region in tissue phantoms containing the respective artificial or intrinsic nuclei. Two separate tests were conducted with pulses applied at PRFs of 0.5 Hz and 100 Hz to investigate the sustainability of cavitation at a very low pulsing rate in which no cavitation memory effects were present as well as a higher pulsing rate in which residual bubbles could be utilized to maintain cavitation on subsequent pulses. The p- for the applied histotripsy pulses were 10.0 MPa, 20.4 MPa, and 42.0 MPa for MB, NC, and intrinsic threshold histotripsy, respectively. These pressure levels were selected to compare the multi-pulse cloud behavior for bubble clouds with similar dimensions for each experimental condition. For the first set of experiments at 0.5 Hz PRF, the low pulsing rate minimized the potential re-stimulation of residual nuclei remaining from bubbles formed on previous pulses to determine if MBs and NCs were destroyed over successive pulses or if they continued to act as viable sources of nucleation over the course for 2,000 pulses. In the second set of experiments at 100 Hz PRF, the higher pulsing rate allowed for the assessment of cavitation sustainability at a more clinically relevant pulsing rate to determine if cavitation could be maintained over the entire 2,000 pulses either by re-nucleating the cavitation bubble cloud or re-stimulating residual bubbles remaining from the prior pulses. Cavitation after each pulse was captured by high-speed optical imaging for 2,000 histotripsy pulses in each sample, and the number of bubbles present after each pulse was compared along with the bubble cloud dimensions, as described above.

Single Bubble Simulation

The bubble behavior (expansion and collapse) and the resulting stress and strain exerted by the bubbles generated from MBs, NCs, and intrinsic nuclei were investigated theoretically using a single bubble numerical model of histotripsy bubbles in a viscoelastic medium (Vlaisavljevich, et al. 2015c, Vlaisavljevich, et al. 2016c, Mancia, et al. 2017, Mancia, et al. 2019). Based on prior work showing that histotripsy bubbles within a bubble cloud appear to remain at a similar size to the bubbles observed just above the cavitation threshold (Vlaisavljevich, et al. 2015c), we compared single bubbles generated from a MB, NC, and intrinsic nucleus at p- levels directly above their respective cavitation thresholds. Our model assumes bubbles arise from free stabilized gas nuclei in all cases, and therefore, we neglect the lipid shell of the MBs as well as the initial nucleation process (i.e. phase change) required to form the initial gas bubbles from NCs and intrinsic nuclei. The initial bubble radii, R₀, were set to representative values for MBs (R₀ = 2,000 nm), NCs (R₀ = 40 nm), and intrinsic nuclei (R₀ = 3 nm) to correlate with experiments. The respective values of 40 nm and 3 nm for the NCs and intrinsic nuclei are inferred based on the maximum radii and collapse times achieved experimentally. Our assumption of a 3 nm intrinsic nucleus was further supported by our previous studies modeling intrinsic threshold histotripsy cavitation (Vlaisavljevich, et al. 2015b, Mancia, et al. 2017, Alavi Tamaddoni, et al. 2018, Mancia, et al. 2019, Wilson, et al. 2019).

Numerical bubble dynamics simulations were performed for three cases representative of experimental conditions for intrinsic and artificial nuclei. For each case, we modeled a free single spherical bubble in a homogeneous viscoelastic medium simulating a 1% agarose phantom. Previous studies describe the theoretical model and numerical methods in greater detail (Warnez and Johnsen 2014). Radial dynamics are governed by the Keller-Miksis equation:

$$\left(1-\frac{\dot{R}}{c}\right)R\ddot{R}+\frac{3}{2}\left(1-\frac{\dot{R}}{3c}\right){\dot{R}}^2=\frac{1}{\rho }\left(1+\frac{\dot{R}}{c}+\frac{R}{c}\frac{d}{dt}\right)\left[p_B-\left[p_{\infty }+p_a\left(t\right)\right]-\frac{2S}{R}+J\right]$$ (E2)

where R is the bubble radius and overdots (^·) denote derivatives with respect to time, t. Physical constants for all simulations include medium density, ρ = 1000 kg/m³, sound speed, c = 1497 m/s, far-field ambient pressure, p_∞ = 101325 Pa, and surface tension, S = 72 mN/m. Given the significant water content of the gel medium, these constants are equal to their values for water at 25°C. Time-dependent terms including the internal bubble pressure, p_B, the acoustic forcing, p_a(t), and the integral of deviatoric stresses in the surroundings, J, are defined subsequently.

The Keller-Miksis equation (E2) is coupled to the energy equation for air inside the bubble by the internal bubble pressure, p_B:

$${\dot{p}}_B=\frac{3}{R}\left(\left(\kappa -1\right)K{\frac{\partial T}{\partial r}|}_R-\kappa p_B\dot{R}\right)$$ (E3)

$$\frac{\kappa }{\kappa -1}\frac{p_B}{T}\left[\frac{\partial T}{\partial t}+\frac{1}{\kappa p_B}\left(\left(\kappa -1\right)K\frac{\partial T}{\partial r}-\frac{r{\dot{p}}_B}{3}\right)\frac{\partial T}{\partial r}\right]={\dot{p}}_B+\frac{1}{r^2}\frac{\partial }{\partial r}\left(r^{2}K\frac{\partial T}{\partial r}\right)$$ (E4)

In the above expressions, T(r, t) is the temperature of the air inside the bubble which has a ratio of specific heats κ = 1.4. The thermal conductivity of air is given by K = K_AT + K_B, where K_A and K_B are empirically determined constants (Prosperetti, et al. 1988, Kamath and Prosperetti 1989). The bubble is assumed to be at equilibrium initially, with an internal bubble pressure equal to p_∞ + 2S/R₀, where R₀ is the initial radius or nucleus size. As discussed previously, the representative intrinsic nucleus, NC, and MB sizes are R₀ = 3 nm, 40 nm, and 2,000 nm, respectively. Boundary conditions were as given in recent work (Mancia, et al. 2019, Wilson, et al. 2019) with ∇T = 0 at the bubble center and T(R) = 25 °C.

In each simulation, the initial gas nucleus was exposed to a time-varying incident pulse, p_a(t):

$$p_a\left(t\right)=\{\begin{array}{ll}-p_{-}{\left(\frac{1+\cos \left[\omega \left(t-\delta \right)\right]}{2}\right)}^n\hfill & ,\left|t-\delta \right|\le \frac{\pi }{\omega }\hfill \\ \hspace{0.17em}0,\hfill & \left|t-\delta \right|>\frac{\pi }{\omega }\hfill \end{array},$$ (E5)

where f = 1 MHz (ω = 2πf) is the frequency of the experimental ultrasound wave. The time delay is δ = 5 μsec and n = 3.7 is a curve-fitting parameter chosen to closely match the shape of experimental waveforms. The peak negative pressure p- was set to 5 MPa, 10 MPa, and 28 MPa for MB, NC, and intrinsic histotripsy conditions, respectively.

The surrounding medium was assumed to behave as a finite-deformation Kelvin-Voigt material (Gaudron, et al. 2014) as previously assumed for histotripsy bubble simulations (Vlaisavljevich, et al. 2016c). The resulting stress integral is given by:

$$J=\frac{E}{6}\left(5-4\left(\frac{R_0}{R}\right)-{\left(\frac{R_0}{R}\right)}^4\right)-\frac{4\mu \dot{R}}{R}$$ (E6)

where E is the Young’s modulus, μ is the medium viscosity, and R₀ is the undeformed or stress-free bubble radius. The Young’s modulus for all simulations was fixed at E = 21.7 kPa, which was the value measured in a previous study for 1% agarose gel under quasistatic conditions (Vlaisavljevich, et al. 2015c). Simulations assumed a viscosity of μ = 0.115 Pa.s, as inferred from single-bubble experiments in agarose gels (Wilson, et al. 2019). The stress-free bubble radius was equivalent to the initial radius, R₀, defined previously for each nucleation condition. After nondimensionalization, the system of ODEs and PDE were solved numerically using previously described numerical methods (Barajas and Johnsen 2017).

We compared the calculated magnitude and spatial extent of stress and strain fields generated by representative cases of MB, NC, and intrinsic histotripsy cavitation. Deviatoric stress, τ, and strain, E, tensors were computed in model agarose following the approach of (Estrada, et al. 2018, Mancia, et al. 2019). In brief, radial and hoop stress fields are given by:

$${\tau }_{rr}=-4\mu \frac{R^2\dot{R}}{r^3}+\frac{2G}{3}\left[{\left(\frac{r_0}{r}\right)}^4-{\left(\frac{r}{r_0}\right)}^2\right]=-2{\tau }_{\theta \theta }$$ (E7)

where $r_0\left(r,t\right)=\sqrt[3]{r^3-R^3+R_0^3}$ relates the radial coordinates before and after deformation.

Strain fields are calculated using the Hencky strain definition:

$$E_{rr}=-2\ln \left(\frac{r}{r_0}\right)=-2E_{\theta \theta }$$ (E8)

Contour plots showing medium deformation and the radial deviatoric stress and strain surrounding bubbles from each nucleation condition were created to visualize the relative spatial extent of these potential tissue damage mechanisms. To quantify the maximum stress and strain as a function of distance from the site of bubble nucleation, we converted stresses and strains into their von Mises invariant equivalents:

$$\overline{\tau }=\sqrt{\frac{3}{2}{\tau }_{ij}{\tau }_{ij}}=\sqrt{\frac{3}{2}\left[{\tau }_{rr}^2+2{\left(-\frac{1}{2}{\tau }_{rr}\right)}^2\right]}=\frac{3}{2}\left|{\tau }_{rr}\right|$$ (E9)

$$\overline{E}=\sqrt{\frac{2}{3}{E}_{ij}{E}_{ij}}=\sqrt{\frac{2}{3}\left[E_{rr}^2+2{\left(-\frac{1}{2}{E}_{rr}\right)}^2\right]}=\left|E_{rr}\right|$$ (E10)

The von Mises equivalents were considered a preferable metric for material damage considerations (Mancia, et al. 2019).

Red Blood Cell Ablation

RBC Phantoms were used to characterize the tissue ablation for histotripsy bubble clouds generated from artificial and intrinsic nuclei. Ablation of the RBCs can be directly visualized as successive pulses turn the embedded cell layer from opaque to translucent as the RBCs are lysed (Maxwell, et al. 2010, Wang, et al. 2012, Lin, et al. 2014, Vlaisavljevich, et al. 2017). Previous studies have also shown that the lesion visualized in RBC phantoms is similar to the lesion generated in tissue identified by histology (Maxwell, et al. 2010, Wang, et al. 2012, Lin, et al. 2014). The RBC phantom was oriented parallel to the direction of sound propagation with the RBC layer centered on the focus (Fig. 1B). The bubble cloud and resulting ablation were recorded by high-speed optical imaging after each pulse (Fig. 1A). For all experiments, 2,000 histotripsy pulses were applied to the RBC phantom, and the camera was triggered twice per pulse to capture the bubble cloud formation (8.5 μs after the pulse arrived), as well as a second image of the resulting RBC lesion formed after each pulse. The first set of RBC ablations was conducted at 0.5 Hz PRF and the second set of experiments was conducted at 100 Hz PRF. At 100 Hz PRF, bubble cloud images were only captured for every twentieth pulse and lesions images were captured following the tenth pulse thereafter, due to the limited triggering rate of our camera set-up. At 0.5 Hz PRF, bubble cloud and lesion images were collected after every pulse. To evaluate the ablation generated from a fully formed bubble cloud with similar cloud dimensions for the three experimental conditions, experiments were performed at p- values of 10.0 MPa, 20.4 MPa, and 42.0 MPa, for MB, NC, and intrinsic threshold histotripsy phantoms, respectively. Three separate samples were tested for each experimental condition, the ablation area after each recorded pulse was measured using MATLAB, as described previously, to create a plot of ablated area vs. pulse number for each experimental condition. The resulting ablation areas were normalized to the area of the respective bubble clouds formed in each case to allow for a comparison of the relative ablative capacity and ablation efficiency of each condition.

Results

Histotripsy Bubble Clouds Generated from Artificial or Intrinsic Nuclei

High-speed optical imaging was used to visualize histotripsy bubble clouds generated at p- ranging from 0.15 to 45 MPa at 0.5 PRF inside agarose tissue phantoms containing gas-filled DFB-MBs, fluid-filled PFH-NCs, or control phantoms without artificial nuclei (Fig. 5). For all phantoms, cavitation bubbles were only observed for conditions above a certain negative pressure, which was ~5 MPa, ~10 MPa, and ~26 MPa for the MB, NC, and intrinsic nuclei phantoms, respectively. As the negative pressure was increased above these minimal values, the number of bubbles and the area covered by the cavitation cloud was significantly increased (Fig. 5). For pressure levels immediately above these threshold values, results for all nuclei conditions showed that the bubble clouds appeared to be well-defined, sharply demarcated clouds that increase in size with larger p-, characteristic of Microtripsy bubble clouds that have been observed in previous studies of intrinsic threshold histotripsy (Maxwell, et al. 2013, Lin, et al. 2014, Vlaisavljevich, et al. 2015b, Vlaisavljevich, et al. 2017) (Fig. 5). However, although well-defined bubble clouds were observed for all cases, a substantial number of peripheral cavitation bubbles were also observed outside of the main bubble cloud for tissue phantoms containing MBs compared to minimal or no peripheral bubbles observed in the peripheral regions for NC and intrinsic nuclei phantoms. For example, the top row of images in Figure 5 shows optical images of bubble clouds formed from MBs with large regions of sparse peripheral cavitation visible outside of the central, densely packed histotripsy bubble cloud. These regions of peripheral cavitation were not observed for NC or intrinsic nuclei phantoms (Fig. 5). Additionally, it was observed that the bubble clouds formed inside the artificial nuclei phantoms for both MBs and NCs appeared to no longer exhibit the well-defined, sharply demarcated boundaries once the pressures were sufficiently large. These effects were observed at pressures above ~16 MPa for MBs and ~30 MPa for NCs. Under these conditions, it became more difficult to differentiate between the primary bubble cloud and any peripherally generated cavitation events, especially for MB phantoms at p- > 16 MPa. This effect was not observed inside any of the intrinsic nuclei phantoms, with all of the resulting bubble clouds showing sharply demarcated boundaries with minimal or no peripheral cavitation up to the maximum p- tested (45 MPa). However, similar behaviors may have been observed for bubble clouds generated in intrinsic nuclei phantoms if higher pressures, beyond those tested in this study, had been investigated (i.e. p- > 50–70 MPa).

Figure 5.

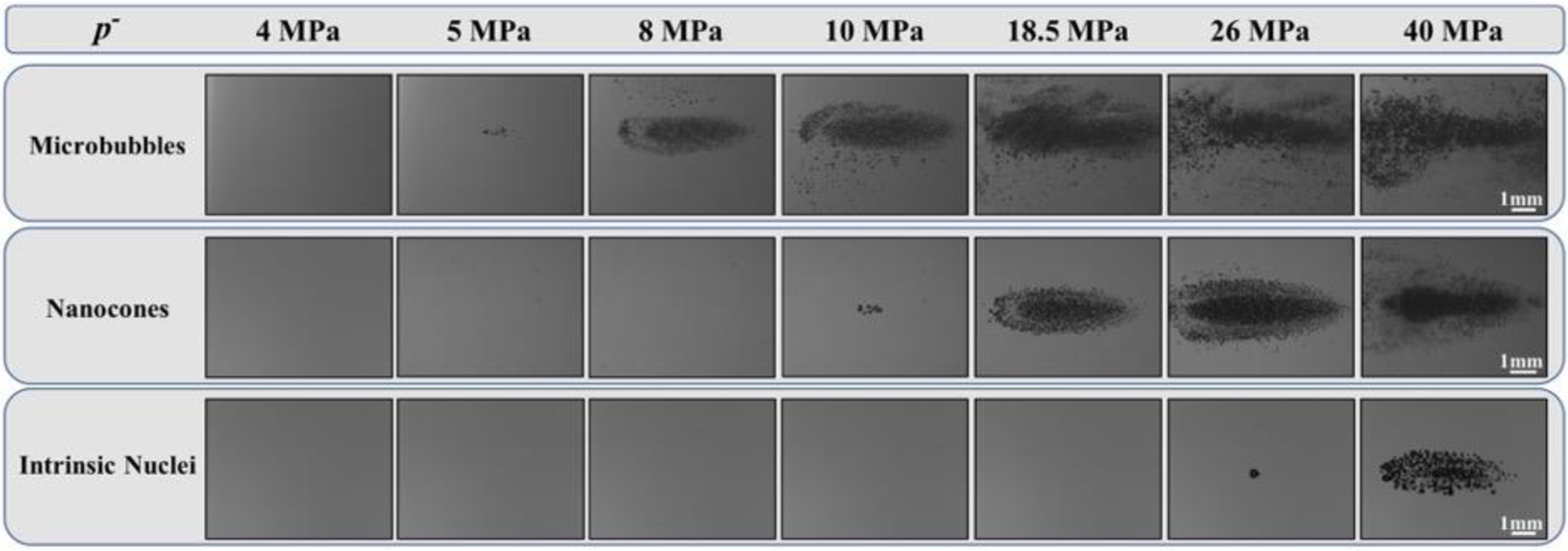
Histotripsy Bubble Cloud Images. Optical images of cavitation bubble clouds generated inside agarose phantoms containing MBs, NCs, and intrinsic nuclei captured by a high-speed camera. Ultrasound propagating left to right.

In addition to the cloud analysis described above, results also showed that individual bubbles within the bubble clouds were smaller in the phantoms containing artificial nuclei (Fig. 5). More specifically, results showed the smallest sized bubbles inside MB phantoms, intermediately sized bubbles inside NC phantoms, and the largest bubbles inside the intrinsic nuclei phantoms. This observation was seen at all pressure levels tested and can be most clearly visualized at pressures directly above the respective cavitation thresholds since the very dense bubble clouds formed at higher pressures made it more difficult to separately visualize individual bubbles within the clouds (Fig. 5). Quantifying the bubble size at pressures directly above the respective cavitation threshold showed average bubble radius values of R_MB = 41.1±6.0 μm, R_NC = 102.9±10.7 μm, and R_HIT = 142.5±12.2 μm (n=20). It is worth noting that the images shown in Figure 5 were taken at a time point when the bubbles were still expanding (8.5μs after the pulse arrival) and thus these measurements do not represent the maximum bubble radius, R_max. However, although not a measure of R_max, the bubble sizes measured at these earlier time points are expected to be representative of the relative changes in bubble expansion for the various conditions. Supplementary Figure 1 shows bubble cloud images at higher magnification in order to better visualize the differences in bubble size for MB, NC, and intrinsic phantoms near their respective thresholds.

Histotripsy Cavitation Threshold Comparison

The histotripsy cavitation threshold was compared for tissue phantoms containing DFB MBs, PFH NCs, or control phantoms with no artificial nuclei. Figure 6 shows the cavitation probability as a function of p- for the three experimental conditions. The cavitation threshold, which was defined as the negative pressure at which p_cav = 0.5, was determined using the curve fitting and statistical analysis described in the Methods section. The measured cavitation threshold for the various experimental conditions was p-_MB = 4.29 MPa, p-_NC = 9.57 MPa, and p-_HIT = 26.5 MPa for MB, NC, and control phantoms, respectively. A distinct threshold behavior was observed for all experimental conditions with σ_mean values of σ_MB = 0.2, σ_NC = 0.2, and σ_HIT = 0.7, demonstrating a similar function of cavitation probability versus pressure, but with lower cavitation thresholds observed for the phantoms containing the respective artificial nuclei.

Figure 6.

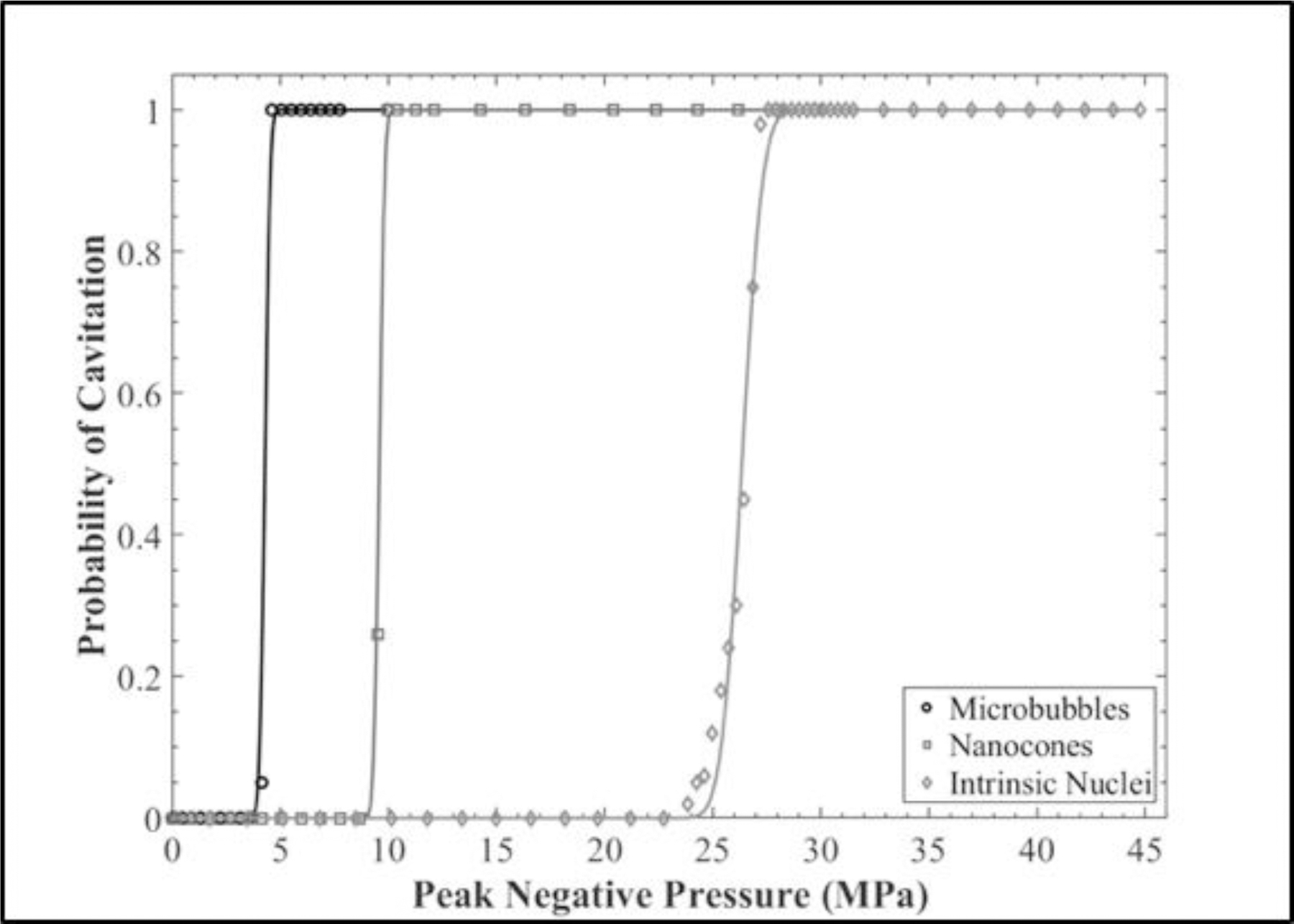
Cavitation Threshold Comparison. Cavitation threshold curves showing the probability of cavitation for each set of experimental conditions plotted as a function of applied p-. The respective cavitation thresholds were found to be p-_MB = 4.29 MPa, p-_NC = 9.57 MPa, and p-_HIT = 26.5 MPa.

Bubble Cloud Dimensions: Predicted vs. Measured

For all experimental conditions, the bubble cloud dimensions in the axial and transverse directions were measured and compared to the cloud dimensions predicted from the 1-D beam profiles, as described in the Methods (Fig. 4). In all cases, the predicted and measured bubble cloud sizes in the transverse and axial directions increased as the p- was increased above the respective cavitation thresholds. The measured axial cloud dimensions shown in Figure 7 ranged from 0.03±0.41 mm (p- = 4.1 MPa) to 6.47±0.23 mm (p- = 10.0 MPa) for MB phantoms, 0.07±0.13 mm (p- = 9.5 MPa) to 8.15±0.11 mm (p- = 28.0 MPa) for NC phantoms, and 0.35±0.41 mm (p- = 26.0 MPa) to 5.71±0.38 mm (p- = 45.0 MPa) for intrinsic phantoms. The measured transverse cloud dimensions shown in Figure 7 showed similar trends, with cloud widths ranging from 0.02±.15 mm (p- = 4.1 MPa) to 2.28±.09 mm (p- = 10.0 MPa) in MB phantoms, 0.06±0.10 mm (p-=9.5 MPa) to 3.64±0.16 mm (p- = 28.0 MPa) in NC phantoms, and 0.05±0.18 mm (p- = 26.0 MPa) to 2.27±0.38 mm (p- = 45.0 MPa) in intrinsic phantoms. A comparison of the predicted and measured bubble cloud sizes showed close agreement (<20% deviation) in both the axial and transverse directions for the majority of experimental conditions (Fig. 7) with larger deviations (>20% ) occurring for intrinsic nuclei in both axial and transverse directions at p- values close to their cavitation threshold where the variation in the size and location of the individual bubbles was large compared to the size of the predicted bubble cloud. Larger deviations were also seen in the transverse direction for intrinsic and NC phantoms at elevated p-. At these very high p- values, it became more difficult to differentiate the areas of peripheral cavitation from the primary bubble cloud, which contributed to the observed deviations. Overall, the results indicated that bubble clouds formed from both artificial and intrinsic nuclei closely matched the region of the focus above their respective cavitation thresholds, allowing for predictable and reproducible bubble cloud formation. It is worth noting that beyond a certain pressure level, the entire pressure field of the transducer surpassed the cavitation thresholds for MB and NC phantoms where the entire field of view became filled with cavitation, and thus no comparison between the predicted and measured bubble clouds was calculated for these p- values.

Figure 7.

Bubble Cloud Size Comparison: Predicted vs. Measured. Plots show the bubble cloud size in the transverse and axial directions compared with the predicted bubble cloud width and length measured using scaled 1-D beam profiles. Results show close agreement between the predicted (dotted line) and measured bubble cloud size (open circles) for both artificial and intrinsic nuclei.

Multi-pulse Cloud Sustainability

To determine the ability of artificial and intrinsic nuclei to produce sustainable cavitation over multiple histotripsy pulses, a set of experiments was conducted in which 2,000 histotripsy pulses were applied to a single focal region in phantoms at PRFs of 0.5 Hz (Fig. 8) or 100 Hz (Fig. 9). Results indicated that well-defined bubble clouds were produced upon the first pulse for all experimental conditions, as observed in the previous experiments shown in Figure 5. For both PRFs tested, the bubble cloud generated inside NC and intrinsic nuclei phantoms showed consistent cavitation behavior sustained for all 2,000 pulses. In contrast, results showed a significant decrease in the number of cavitation bubbles and the size of the bubble cloud generated inside the MB phantoms over the course of multiple pulses, with only a few remaining bubbles generated after 2,000 pulses. This finding, which was observed for both the lower PRF (0.5 Hz) (Fig. 8) and higher PRF (100 Hz) (Fig. 9) conditions, was likely due to MBs being destroyed by the histotripsy process. In addition, the results from the 100 Hz PRF experiments suggest that the “cavitation memory” effect, which has previously been reported (Wang, et al. 2012, Duryea, et al. 2015), was not sufficient for maintaining sustained bubble cloud activity in the MB phantoms.

Figure 8.

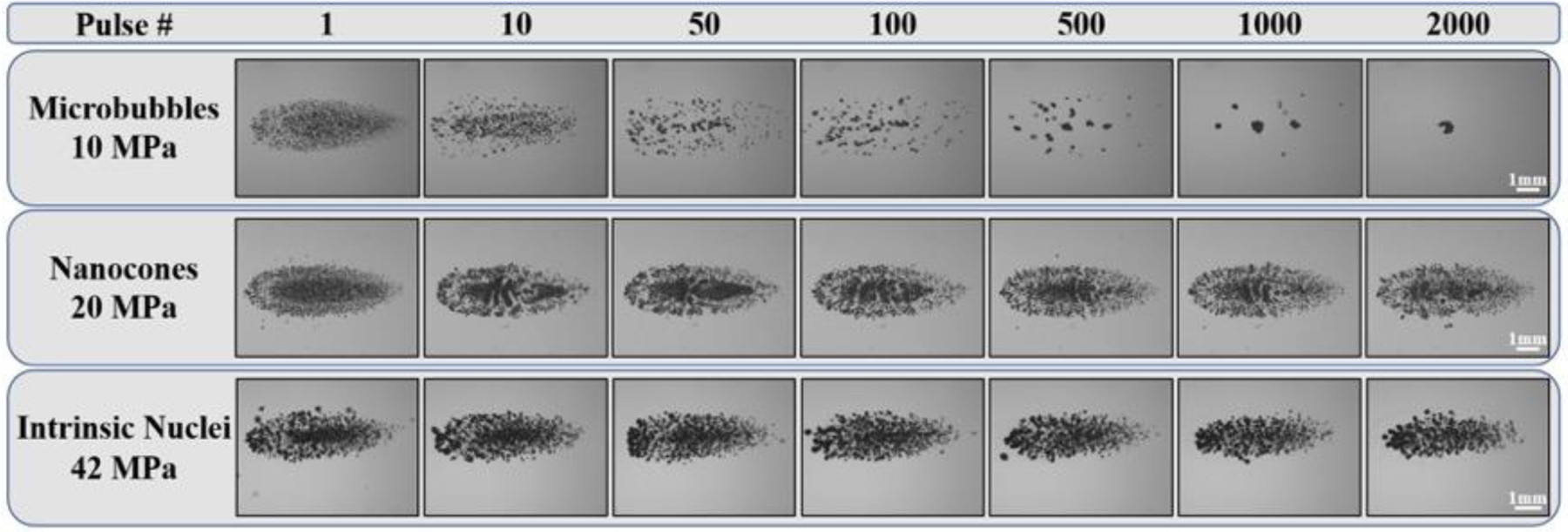
Multi-pulse Cloud Sustainability: 0.5 Hz PRF. Optical images of bubble clouds produced at a single focal point in tissue phantoms at a PRF of 0.5 Hz for 2,000 applied histotripsy pulses. Ultrasound propagating left to right.

Figure 9:

Multi-pulse Cloud Sustainability: 100 Hz PRF. Optical images of bubble clouds produced at a single focal point in tissue phantoms at a PRF of 100 Hz for 2,000 applied histotripsy pulses. Ultrasound propagating left to right.

In addition to the reduction in the number of cavitation bubbles inside the MB phantoms with increasing pulse number, the results from the multi-pulse experiments in NC and intrinsic nuclei phantoms also showed changes in the bubble cloud appearance over the course of 2,000 applied pulses. At the lower PRF (0.5 Hz), the bubble clouds generated in both NC and intrinsic nuclei phantoms appeared to maintain the same well-defined cloud dimensions characteristic of Microtripsy bubble clouds (Fig. 8). However, at the higher PRF (100 Hz), there was an observable change in the dimensions of the bubble clouds generated inside the NC and intrinsic phantoms, which were observed as smaller, less dense, and less well-defined bubble clouds after the first pulse (Fig. 9). This change in bubble cloud behavior appeared to be due to cavitation memory effects in which residual bubbles from one pulse were reignited on the following pulse, resulting in clouds with significantly different features than the cloud observed on the first pulse. Results further showed that the cavitation memory effects did not merely result in the formation of bubbles in similar locations as the prior pulse, as has previously been reported, but these residual nuclei also appeared to have the added effect of preventing the formation of newly nucleated bubbles throughout the focal region on subsequent pulses. By preventing the nucleation of new bubbles, the cavitation memory effects were observed to prevent the formation of the dense, well-defined bubble clouds covering the entire focal region, which were observed on the first pulse (and for all pulses in the 0.5 Hz PRF experiments). In addition to these effects of cavitation memory on the cloud behavior, deviations from the predicted bubble cloud dimensions beyond the initial pulses at 100 Hz PRF seemed to be an indication of “focal sharpening” effects that have previously been reported to alter the cavitation pattern in histotripsy (Wang, et al. 2011). A similar focal sharpening effect was observed for the first ~500 pulses in control phantoms treated at 100 Hz, with the bubble cloud returning to the predicted dimensions after ~1,000 pulses, which likely corresponded to a point at which the agarose tissue phantom was sufficiently ablated into a fluid-like homogenate.

Single Bubble Behavior and Stress-Strain Simulation

The radial deviatoric stress (E7) and radial strain (E8) exerted on the surrounding tissue by histotripsy bubbles generated from a representative MB, NC, and intrinsic nucleus are shown (top to bottom) in Figure 10. Although only radial components are shown in Figure 10, we note that hoop stresses and strains act simultaneously and at half the magnitude (Mancia, et al. 2017). In these contour plots, medium deformation by the growing bubble is shown in white while colors correspond to the magnitudes of compressive (negative) and tensile (positive) radial stress and strain. Results demonstrated reduced histotripsy bubble expansion from artificial nuclei at lower p-. Specifically, bubbles nucleated under each condition achieved maximum radii of 193 μm, 71 μm, and 58 μm for intrinsic, NC, and MB cases, respectively. In addition, results showed that this reduced bubble expansion corresponded to a decrease in the stress and strain exerted on the surrounding tissue during both bubble expansion and collapse. For all conditions, the bubbles show similar qualitative behavior, inducing large transient stresses and strains on the medium with the largest stresses and strains occurring at the maximum bubble radius and closest to the bubble wall. Radial deviatoric stress is compressive during bubble growth and early collapse but becomes increasingly tensile as the bubble reaches its minimum radius. The absolute maximum radial stresses are compressive (negative) and occur at the maximum bubble radius, but a significant relative maximum in compressive stress occurs at the onset of bubble growth in each case. Although our model assuming continuous tissue deformation risks overestimating the stress and strain developed closest to the site of nucleation, this possibility does not affect stress and strain developed within the length scale of a single cell and consequently does not affect predicted damage radii (Mancia, et al. 2019). At a distance of 10 microns from the site of nucleation, the magnitude of maximum radial stress was 1.8 MPa for the intrinsic nucleus, 0.25 MPa for the NC, and 0.16 MPa for the MB. Radial strains were also compressive and maximized at maximum bubble radius. Respective maximum strain magnitudes of approximately 6 μm/μm, 4 μm/μm, and 3.5 μm/μm were developed in that tissue at locations 10 microns from the initial intrinsic, NC, and MB nuclei. With increasing distance from the site of nucleation, these stresses and strains attenuated significantly.

Figure 10.

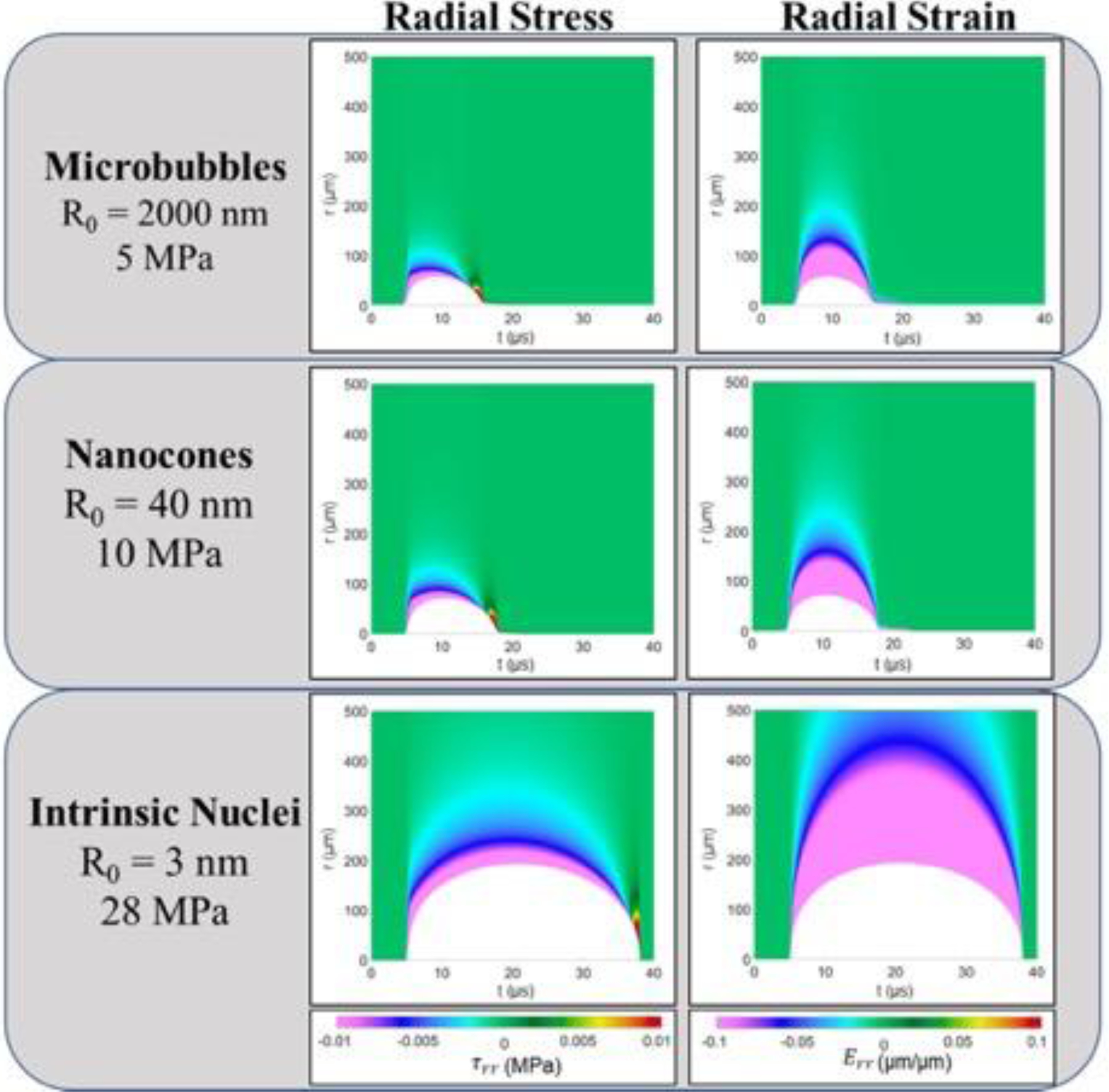
Single Bubble Simulations. Radial deviatoric stress (left column) and radial strain (right column) surrounding a bubble for the three representative nucleation conditions. Contour plots show field quantities at material coordinate, r, as a function of time. White portions of each plot show the extent of material deformation by the bubble as a function of time under each condition.

The maximum von Mises stress and strain (E9 – E10) induced in the surrounding media was also plotted as a function of distance from the bubble, with results showing decreases in the maximum stress and strain with increasing distance from the initial bubble for all nucleation conditions (Fig. 11). This rapid attenuation of stress and strain has also been observed in previous studies of histotripsy bubble dynamics (Vlaisavljevich, et al. 2016c). Comparing histotripsy bubbles generated from MBs, NCs, and intrinsic nuclei showed that bubbles arising from intrinsic nuclei generated larger stresses and strains on the surrounding tissue than what was observed for artificial nuclei at all distances from the bubble, with the smallest values seen in the MB case. Maximum von Mises strain traces for each nucleation condition also showed greater distinction than corresponding maximum stress traces, supporting the proposed use of von Mises strain as a metric for ablation extent (Mancia, et al. 2019). Together, these results support the hypothesis that histotripsy bubbles formed from artificial nuclei at lower p- will exert less stress and strain on the surrounding tissue and will thus result in a smaller region of damage surrounding the bubble compared to histotripsy bubbles formed from intrinsic nuclei at higher p-.

Figure 11.

Single Bubble Simulation: Max Stress and Strain Comparison. Plots show the maximum von Mises (A) stress and (B) strain plotted as a function of distance from the nucleus for the three representative nucleation conditions. Results showed a significant decrease in the maximum stress and strain exerted on the surrounding tissue for artificial nuclei compared to intrinsic nuclei simulations.

Histotripsy Ablation in RBC Phantoms

Agarose tissue phantoms embedded with RBC layers were used to compare the histotripsy ablation capacity for bubble clouds generated from MBs, NCs, and intrinsic nuclei. For all phantoms, histotripsy (2,000 pulses) was applied to a single point in the RBC layer at 0.5 Hz or 100 Hz PRF. Optical imaging captured the bubble cloud on the pulse and lesion area in between pulses, with the extent of the damaged area increasing with increasing pulse number (Fig. 12, Fig. 13). For all cases, the ablated area was confined to the regions of the focus in which cavitation was observed. For the lower PRF (0.5 Hz) experiments, histotripsy generated well-defined lesions in intrinsic phantoms, with near-complete ablation of the focal volume observed within ~500–1000 pulses (Fig. 12). These results matched previous studies showing histotripsy can predictably and reproducibly produce completely ablated lesions with sharply demarcated boundaries between the treated region and the remaining undisturbed RBCs (Fig. 12). Results for 0.5 Hz PRF experiments inside NC phantoms demonstrated a similar degree of focal adherence to what was observed in the intrinsic nuclei phantoms (Fig. 12). However, NMH did not remove the entirety of the focal region within 2,000 pulses and showed a decrease in the efficiency of ablation compared to control treatments, with more pulses required to ablate the RBCs in the region exposed to the bubble cloud (Fig. 12). Results for MB phantoms at 0.5 Hz showed a significant reduction in the extent of RBC ablation achieved after 2,000 pulses compared to both NC and intrinsic nuclei phantoms, with only the periphery of the focal region and small regions within the focal zone ablated after 2,000 pulses (Fig. 12).

Figure 12.

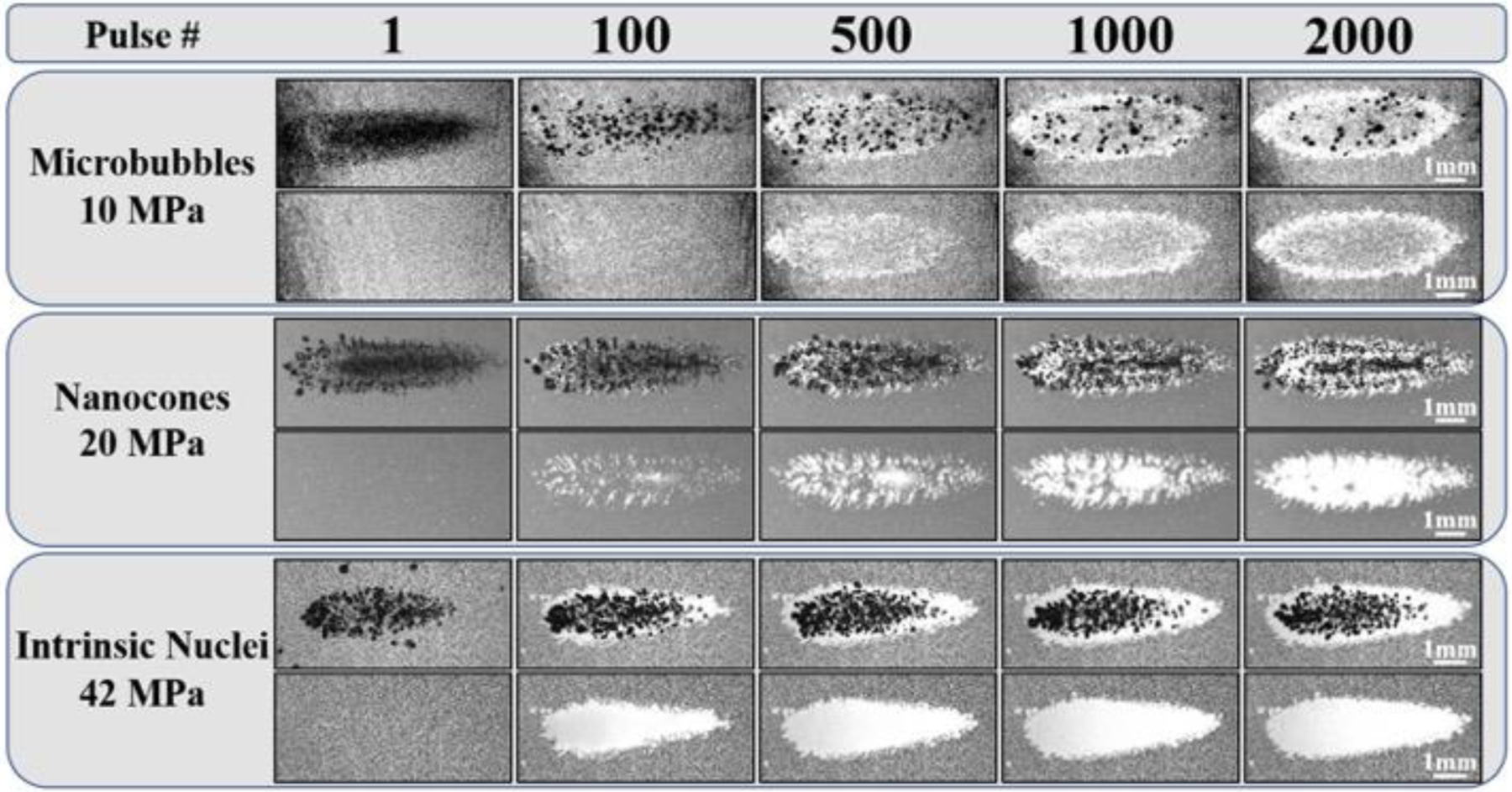
RBC Ablation: 0.5 Hz. Images show the cavitation bubble cloud (dark) and immediately resulting histotripsy lesions (white) generated in RBC phantoms (grey) containing MBs, NCs, and intrinsic nuclei at 0.5Hz PRF. Ultrasound propagating left to right.

Figure 13.

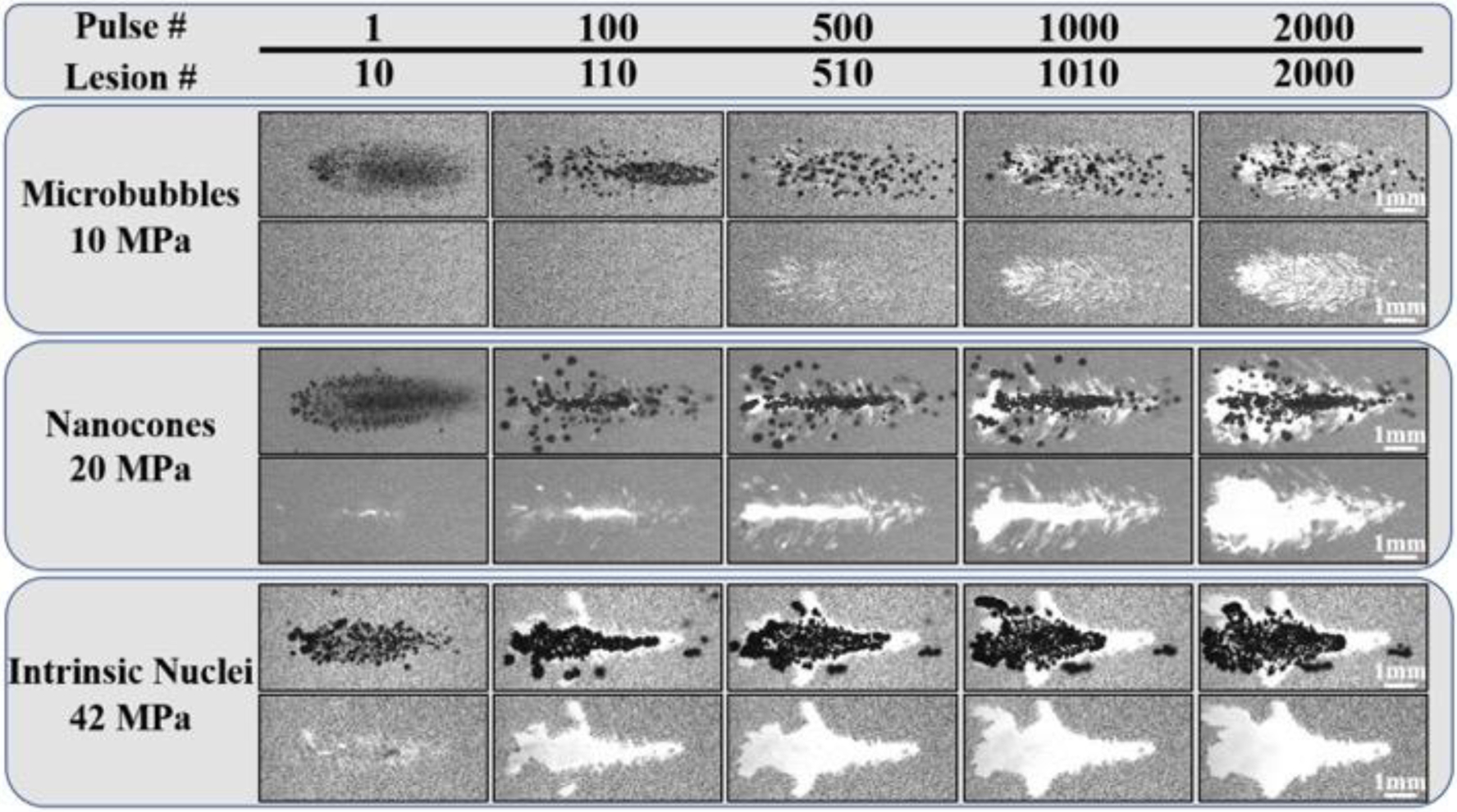
RBC Ablation: 100 Hz. Images show the cavitation bubble cloud (dark) and histotripsy lesions (white) generated in RBC phantoms (grey) containing MBs, NCs, and intrinsic nuclei at 100 Hz PRF. Ultrasound propagating left to right.

Results for RBC ablation experiments at 100 Hz PRF (Fig. 13) showed similar trends to the lower PRF treatments (Fig. 12), with more rapid and complete RBC ablation generated in the intrinsic nuclei and NC phantoms compared to the MB phantoms. Results also showed less well-defined ablation zones generated for both intrinsic nuclei and NC phantoms exposed to histotripsy at 100 Hz PRF compared to 0.5 Hz PRF, due to the less well-defined bubble clouds that were observed over multiple pulses at 100 Hz (Fig. 13). Results for MB phantoms treated at 100 Hz showed a similar ablated area to MB phantoms treated at 0.5 Hz. However, the ablation zone generated in MB phantoms at the higher PRF was more uniformly distributed throughout the focal region (Fig. 13) compared to the lower PRF case in which the ablation was primarily observed on the periphery of the focal zone (Fig. 12).

The ablation efficiencies observed in the RBC experiments were quantitatively compared by plotting the ablation area as a function of pulse number. Figure 14 shows a quantitative comparison of the normalized lesion area as a function of pulse number for MB, NC, and intrinsic nuclei RBC phantoms (n=3) at 0.5 PRF (Fig. 14A) and 100 PRF (Fig. 14B). The normalized lesion areas increased rapidly with pulse number in the intrinsic nuclei phantoms, achieving >75% ablation of the focal region within <250 pulses and resulting in 99.6±5.9% of the focal zone after 2,000 pulses at 0.5 PRF (Fig. 14A). At 100 Hz, histotripsy in intrinsic phantoms showed a slightly reduced efficiency with 75% of the ablation zone being ablated after ~1,000 pulses and a final ablation zone of 89.2±8.3% of the focal region. RBC ablation in NC and MB phantoms showed a significant decrease in the efficiency of ablation compared to intrinsic nuclei phantoms, as can be observed by the respective slopes of the ablation curves (Fig. 14). In addition, the final ablation zones were also measured to be 70.4±10.9% and 20.7±10.7% of the focal region at 0.5 PRF NC and MB phantoms, respectively (Fig. 14A). Unlike the intrinsic nuclei phantoms, ablation efficiency in NC phantoms did not show a decrease at 100 PRF and resulted in a final ablation zone of 71.8±9.1% of the focal region after 2,000 pulses (Fig. 14B). For the MB phantoms treated at 100 Hz, the final ablation zone (31.7±4.0%) was slightly larger than what was observed at the lower PRF, with no clear trend in the ablation efficiency observed between these two PRFs (Fig. 14). Based on these results, it is expected that NCs would have eventually achieved a complete ablation of the focal region for both PRFs if more pulses had been applied beyond the 2,000 pulses tested in these studies, matching the final ablation zones in intrinsic nuclei phantoms. Alternatively, it is hypothesized that a complete ablation would never have been achieved in the MB phantoms even with additional pulses since the bubble clouds were not sustained over the course of multiple pulses (Fig. 8, Fig. 9).

Figure 14.

RBC Ablation Plots. Plots show the ablation area formed in the RBC agarose gel phantoms containing MBs, NCs, and intrinsic nuclei for A) 0.5 Hz and B) 100 Hz PRF histotripsy conditions. The applied p- was 10.0 MPa, 20.4 MPa, and 42.0 MPa for the MB, NC, and intrinsic nuclei conditions, respectively.

Discussion

In this study, the bubble cloud behavior and ablative capacity of histotripsy generated from artificial nuclei (gas-filled MBs or fluid-filled NCs) were evaluated in comparison to intrinsic threshold histotripsy. Overall, results supported our hypothesis that artificial nuclei are capable of generating histotripsy cavitation bubble clouds at a significantly lower p- compared to intrinsic histotripsy. Results further supported our hypothesis that bubble clouds generated from artificial nuclei at lower pressures would consist of smaller bubbles that exert less stress and strain on the surrounding tissue, thereby reducing the ablative capacity of histotripsy under these conditions. Finally, results showed that NCs could be utilized for sustained cavitation nucleation over multiple pulses, whereas MBs would be destroyed during the cavitation process, further reducing the ablative capacity of histotripsy bubble clouds generated from MBs. The overall findings of this study expand upon previous work developing particle-seeded histotripsy methods, resulting in important insights that will be useful to the future development of these methods for specific clinical applications.

In the first part of this study, the effects of artificial nuclei on the cavitation threshold and bubble cloud behavior were investigated. For both MB and NC phantoms, the cavitation threshold was significantly lower than the histotripsy intrinsic threshold and maintained a distinct threshold behavior. With increasing pressure, the bubble clouds’ dimensions were observed to increase in size as predicted, with a close correlation between the predicted and measured bubble clouds. The physical characterization of the bubble clouds generated from artificial nuclei showed dense bubble clouds with distinct boundaries. Together, these findings demonstrate that characteristic Microtripsy bubble clouds can also be achieved for bubble clouds generated from artificial nuclei, which is a promising finding for performing particle-mediated histotripsy treatments with the high predictability that has previously been shown for intrinsic threshold histotripsy (Lin, et al. 2014). However, it is worth noting that significantly more peripheral cavitation was observed in MB phantoms compared to NC and intrinsic nuclei phantoms, suggesting the potential for more off-target effects for histotripsy treatments generated from gas-filled nuclei. Furthermore, results from experiments at very high p- values showed that the bubble clouds generated from both types of artificial nuclei became less confined and were accompanied by a significant amount of peripheral cavitation, suggesting that an upper limit on the in-situ pressure levels used in particle-mediated histotripsy should be considered to limit potential off-target cavitation injury. Additionally, at these higher pressures, the bubble clouds appeared to show two distinct regions that included a darker center region and a sparser peripheral region. Although both of these regions proved capable of ablation in the RBC phantoms, additional studies will be necessary to investigate the cause of this apparent spatial difference in cloud density.

In addition to the cloud characteristics, results from this work also showed that individual bubbles within the clouds generated from artificial nuclei were significantly smaller than individual bubbles inside the clouds generated from intrinsic nuclei. This finding, which was observed in both the single bubble simulations as well as experiments, matched our hypothesis that bubble expansion is reduced in particle-mediated histotripsy due to the lower p-. Results showed the smallest bubble size in MB phantoms, intermediate size for NC phantoms, and the largest bubbles for intrinsic nuclei, with the single bubble simulations showing that these differences directly correlated with the magnitude of the stress and strain that was exerted on the surrounding tissue as well as the area around each bubble exposed to high stress and strain. Results from the single bubble simulations showed a significant decrease in the maximum stress and strain exerted on the surrounding tissue for the artificial nuclei conditions due to the reduced bubble expansion. These findings suggest that particle-mediated histotripsy treatments may require higher doses (more pulses) to ablate a target tissue and may have difficulty ablating tissues with higher mechanical strength. By the same reasoning, this finding may also suggest that particle-mediated histotripsy approaches may enhance the tissue-selective features of histotripsy (Vlaisavljevich, et al. 2014a), potentially allowing for safer and more effective treatment strategies for soft tissues located near critical structures with high mechanical strength such as blood vessels, nerves, and bile ducts. Future work is planned to explore this possibility by comparing histotripsy generated from artificial and intrinsic nuclei in tissues with a range of mechanical properties. These studies will be aided by a more complete understanding of the physics of cavitation damage, including the consideration of strain-rate-dependent tissue properties (Estrada, et al. 2018, Mancia, et al. 2019)

In the second part of this study, the effects of artificial and intrinsic nucleation on histotripsy bubble cloud dynamics were investigated over multiple pulses to determine if the various nuclei types could be used to sustain cavitation activity. The results indicated that NCs and intrinsic cavitation nuclei were capable of sustaining bubble cloud activity, whereas MBs failed to sustain a dense cavitation cloud beyond tens of pulses, suggesting that MBs are destroyed by the histotripsy process and therefore function as cavitation nuclei only for the initial pulses. Histotripsy bubbles within the focal region beyond a few hundred pulses in MB-seeded histotripsy seemed to be growing in the same location as previous pulses, suggesting that they were formed from the re-expansion of dissolved gas rather than being the result of new cavitation bubbles formed from intact MBs. This effect was observed to be slightly more prevalent for 100 Hz PRF, but this PRF was still insufficient to maintain a bubble cloud over the course of 2,000 pulses. It is possible that more sustained cavitation, and thus more complete ablation, could be maintained at very high PRFs above the 100 Hz tested in this study, which is a possibility that should be explored in future studies of MB-seeded histotripsy.

Another interesting observation from multi-pulse experiments was that, although sustained bubble clouds were formed in NC and intrinsic nuclei phantoms at both PRFs, significant deviations in the bubble cloud characteristics were observed after a few pulses at 100 Hz. More specifically, the bubble clouds at 100 Hz PRF became less well-defined, less dense, and covered a smaller portion of the focal region. These changes were likely due to cavitation memory and focal sharpening effects that have been reported in previous histotripsy studies (Wang, et al. 2011, Wang, et al. 2012, Duryea, et al. 2015). Although the bubble clouds became more well-defined within the focal region after a sufficient number of pulses, likely due to the tissue phantom being broken down, this finding highlights the need for improved strategies capable of maintaining Microtripsy bubble clouds during histotripsy procedures at clinically relevant PRFs. Future work should explore these potential strategies, such as utilizing the residual bubble removal strategies previously developed by Duryea et al. (2015).

Overall, the results from the multi-pulse experiments show that the type of artificial nuclei used in particle-mediated histotripsy procedures should be considered when planning treatments. Fluid-filled particles can provide consistent and reproducible nucleation of cavitation clouds over the course of a histotripsy treatment while gas-filled particles showed only limited cavitation nucleation potential beyond the first pulses, at least within the PRF range explored in this study. This result indicates that the application of MBs for generating histotripsy bubble clouds is likely only preferred in applications where temporary, limited cavitation capacity is desirable, such as for the partial ablation of tumors for enhanced tissue permeability, drug delivery, or immune activation. Alternatively, histotripsy generated from MBs may also be feasible for applications in which MBs are circulated or replenished at the focus throughout the treatment, such as in particle-mediated histotripsy thrombolysis (Bader, et al. 2015, Bader, et al. 2016). In contrast, results show that fluid-filled cavitation nuclei can provide more consistent and sustained nucleation, similar to conventional intrinsic threshold histotripsy, allowing for a wider range of applications in which complete ablation of a targeted tissue volume is desired.

In the final part of this study, we tested the hypothesis that the extent and rate of ablation would be significantly decreased for histotripsy produced from artificial cavitation nuclei due to the decreased bubble expansion (both NCs and MBs) and decreased cloud sustainability of multiple pulses (MBs only). Results from the ablation experiments supported our hypotheses by demonstrating that, although well-defined and densely populated bubble clouds were initially generated from MBs and NCs, the ablation zones formed over 2,000 pulses were less complete compared to intrinsic threshold histotripsy. This effect was most pronounced in the MB phantoms, which showed only ~20–30% of the focal region ablated after 2,000 pulses. Treatments in NC phantoms showed nearly complete ablation after 2,000 pulses that more closely matched the intrinsic threshold histotripsy control phantoms. However, the rate of ablation was still reduced for NC phantoms compared to the histotripsy controls. The observed decrease in ablation efficiency for histotripsy clouds generated from artificial nuclei supports our hypothesis that the smaller bubbles exert less stress and strain on the surrounding tissue and also expose a smaller region surrounding each bubble to the high strain needed to rupture the targeted cells. Additionally, MB instability over multiple pulses resulted in incomplete ablation of the targeted region, as predicted by the multi-pulse cavitation experiments. Of note, it may be possible to circumvent this limitation and maintain the concentration of MBs at a treatment location through sustained delivery of MBs to the treatment location to improve ablation capacity for specific applications, which is worth exploring in future studies of MB-mediated histotripsy. In addition, although solid, gas stabilizing nanoparticles (i.e. nanocups) (Kwan, et al. 2015, Thomas, et al. 2019) were not tested as part of this study, we would hypothesize that these nuclei would eventually result in complete ablation of the target volume since prior work with these types of solid nanoparticles has shown they can provide stable cavitation nucleation over multiple pulses.

Conclusion

This work investigated the bubble cloud behavior and ablative capacity of histotripsy bubble clouds generated from artificial cavitation nuclei compared to bubble clouds generated from intrinsic nuclei. The results of this study show the potential of artificial nuclei to seed precise Microtripsy-like bubble clouds at pressures significantly below the histotripsy intrinsic threshold while also highlighting key differences in the bubble behavior, multi-pulse sustainability, and ablative abilities for these respective histotripsy conditions. Results demonstrated both types of artificial nuclei significantly reduced the histotripsy cavitation threshold and resulted in dense bubble clouds with dimensional fidelity to the region of the focus above the respective cavitation thresholds. Multi-pulse experiments showed that NCs repeatedly produced cavitation similar to histotripsy from intrinsic nuclei, whereas MBs failed to sustain a dense, populous bubble cloud beyond tens of pulses. Lastly, the RBC ablation testing demonstrated that cavitation clouds from artificial nuclei were capable of ablating the tissue phantoms but had a reduced ablation efficiency compared to intrinsic threshold histotripsy. Overall, this study demonstrates that artificial nuclei can offer a means to generate cavitation below the intrinsic threshold, but the differences in the behavior of the cavitation bubble clouds and ablative capacity should be considered when developing particle-mediated histotripsy strategies for specific clinical applications.