Abstract
The determination of the optical properties of a turbid medium is a major topic in the field of optics. Generally, they comprise the parameters µa, µs, g and n. There is, however, a lack of techniques for the direct determination of the scattering coefficient µs. This study, therefore, proposes the random laser (RL) as a tool to directly measure µs - and not . Evidence is found that it is possible to determine µs in the diffusive regime by means of the RL. Based on these findings, a local model of the RL is developed and presented in this study.
1. Introduction
The optical properties of a turbid medium are generally understood to comprise the parameters (absorption coefficient), (scattering coefficient), (anisotropy factor) and . The determination of the first three is a major topic in the field of optics and, therefore, a multitude of different techniques to measure them have so far been presented. [1]
By introducing the reduced scattering coefficient , this parameter set can be reduced by one dimension: . This is an approximation that is usually valid, but can lead to errors if the source-detector separation in e.g. diffuse reflectance spectroscopy or the size of the objects to be measured, respectively, are smaller or similar to as approximations of the phase function may be wrong. [2,3] It is crucial in this context that most of the reliable techniques for the determination of optical properties only provide this reduced parameter set - consequently, they cannot be used for applications targeting the capillary network or other similarly small structures. For such cases, a direct determination of the scattering coefficient is essential.
It is also worth noting at this point that latest research results show that it is even a great challenge to precisely determine and . [4,5]. Hence, the measurement of all three optical properties mentioned is expected to be even more defiant.
At present, there are essentially two ways to separately estimate both and . Among them, inverse techniques form the gold standard: Total reflection as well as total and collimated transmission are measured, and from these values the three parameters of the optical properties are derived using either inverse adding doubling [6,7] or an inverse Monte Carlo simulation. [8] Since the measurement of the collimated transmission is, however, still afflicted with errors [9], only scarce data on and can be found in the literature compared to that of . [10]
The second approach, the employment of optical coherence tomography (OCT) to separately measure the two parameters mentioned [11], also has - besides the advantage that data can be acquired spatially resolved [12] - significant disadvantages. First, as an OCT is only capable of measuring the transport coefficient , this technique can only be applied in wavelength regimes for which the absorption coefficient is significantly smaller than the scattering coefficient (so that ). This limits the spectral window. Second, this method only works for the wavelength region of the OCT itself, which limits the spectral range of the scattering coefficient. Third, the high spectral bandwidth of the OCT leads to systematic errors in the measurements as a single value is provided for the whole spectral range of the OCT.
From the two preceding paragraphs, it becomes apparent that there is a lack of techniques for the direct determination of the scattering coefficient . Even though we were able to show in a previous study that can be measured with a high precision in the presence of absorbers, this approach has the downside of working only with lasers and, thus, with a limited available wavelength range. [13]
The aim of this study is, therefore, to investigate whether it is possible to use a random laser (RL) as a tool to measure this scattering coefficient . This distinguishes the present investigation from an already existing study which was only able to use the RL to determine the reduced scattering coefficient . [14,15] Furthermore in this study, a setup is introduced that is further simplifying the measurement.
The working principle of a RL is quite similar to that of a conventional laser: When the total gain by stimulated emission is larger than the losses within that setup, the laser system reaches a threshold and lases. However, RLs are distinguished from conventional lasers because of their unique feedback mechanism: In a conventional laser, the feedback is provided by an optical cavity built of mirrors, while the feedback in a RL is realized through multiple scattering by scattering particles. This multiple scattering increases the path length (or dwell time) of light in the gain medium and, thus, enhances the light amplification by stimulated emission. [16]
In the perspective of constructions, there are two classes of RLs. [17] One consists of active scatterers such as rare earth doped powder [18], semiconductor powder [19] or polymer films [20] which provide both gain and multiple scattering at the same time.
The second class, in contrast, is characterised by the fact that the scatterers are added separately to the gain media. In this case, organic fluorescence dyes are widely used as laser gain media, while the feedback in such a dye-based RL comes from either active scatterers like ZnO powder [21] or passive scatterers like powder. [22] Besides, dye-doped nematic liquid crystals [23] provide another approach to generate a RL since the variation of the external electric field gives rise to the disorder in the previously homogenously oriented liquid crystal. In the last two decades, finally, biological tissues as another new type of scatterers are employed together with gain media for the RL emission. [24–27]
Summing up what has been mentioned so far, it becomes evident that while in a conventional laser scattering would remove the photons from the trajectory within the optical cavity, it essentially determines the properties of the RL. This fact, not least, gave rise to the idea of a new type of optical sensor in which a change in the RL emission allows to draw conclusions about variations within the RL system. [14,28–31] In this context, relevant parameters are a change in the emission light intensity, the spectral line-width and the RL emission modes as well as a wavelength shift of the emission light (either a redshift or a blueshift, depending on the concentration of the laser dyes or scatterers and, thus, on the RL regime). [32]
There is evidence, to give a few examples, that it is possible to differentiate between cancerous and healthy tissue [24], among different malignant grades of cancerous tissue [33] or between skin, fat, muscle and nerve tissue [31] based on the number of laser modes. Likewise, a wavelength shift of 0.55 nm in the emission peaks could be observed when applying strain to bone (as partially disordered biological nanostructure that provides multiple scattering) immersed in dye solution and pumped with a pulsed laser. [28]
The latter approach is based on the fact that the spectral emission wavelength can be tuned, either by external parameters such as pumping, temperature and electricity, or by internal ones such as a change in the scattering coefficient. [17] In the authors’ particular RL system based on dye, the peak wavelength is shifting further to longer wavelengths when increasing the scattering concentration. [14,15,22] This phenomenon was attributed to dye reabsorption which occurs because the emission spectrum of the laser radiation overlaps with the dye absorption spectrum: As the scattering concentration influences the dwell time of the light in the medium, an increased scattering coefficient leads to an enhanced wavelength redshift in their case. [34]
The above could indicate that there seems to be a correlation between variations within the RL system and its emission. So far, however, it has not yet been investigated whether macroscopic measurements of the spectra of the RL allow to draw conclusions about its intrinsic optical properties, especially about the scattering coefficient.
This is the starting point for the present study, which examines the behaviour of the RL as a function of the scattering coefficient and the concentration of the fluorescence dye. With this, parameters within the RL emission should be identified that only depend on the scattering coefficient of the RL. In doing so, it is the aim of this study to relate macroscopic measurements of the RL spectra to the associated scattering coefficients and to explain the effects by which this is mediated.
2. Materials and methods
This section consists of four parts. In the first part, the setup is presented. Afterwards, the method for measuring the peak shift of the fluorescence is explained. The third part shows the parameters of the RL experiment. The last part describes the theoretical considerations.
2.1. RL experimental setup
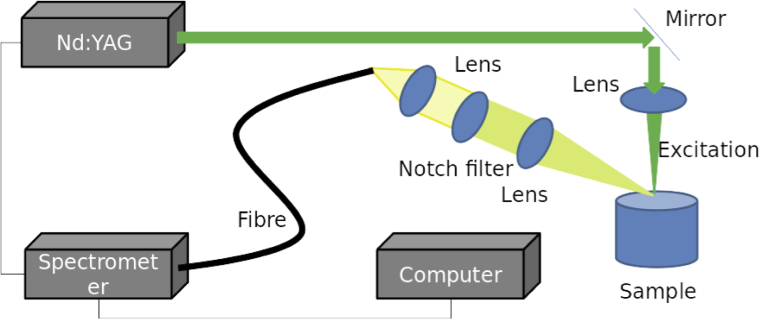
The experimental setup for the generation of the RL is schematically shown in Fig. 1. It mainly consists of a light source for excitation, optics to collect the light emission from the surface of the phantom and devices to measure the spectra.
Fig. 1.
Experimental setup for the generation of the RL. The Nd:YAG laser is focussed on the sample and from there the emitted light is collected by the collection optics and coupled into a fibre, guiding the light to the spectrometer for the analysis.
The light source used for the excitation is a frequency-doubled pulsed Nd:YAG laser (Quantel Q-smart 450, France; , 5 ns). Its output intensity is adjusted by varying the Q-switching delay; pulse intensities in the range from 18 mJ to 40 mJ are realised. A mirror and a lens are used to guide and focus the laser beam to the surface of the sample.
The collecting optics consist of two convex lenses and a notch filter working at the working wavelength of . The emission signal is coupled into a fibre and detected by a spectrometer (Andor Mechelle ME5000 Echelle, UK) equipped with an ICCD camera (Andor A-DH334T-18F-03 USB iStar ICCD detector, UK). The beginning of the spectrometer acquisitions is triggered by the output signal of the laser without delay. The measuring time is 2000 ns which is enough to cover the duration of the emission pulse. The emission spectra are extracted from the spectrometer and further evaluated with Python scripts.
The sample is measured in a beaker and both excited and emitted light are guided and collected from the top. This configuration is chosen to eliminate the influence of any container walls on the emission intensity. The sample is filled in a beaker with a diameter of 50 mm and it is filled with 75 ml solution leading to a filling height of about 38 mm. The size of the focal spot is 0.25 mm in diameter. Furthermore, the focal spot is not completely focused.
2.2. Flourescence peak shift and path length
As already mentioned in the introduction of this paper, the peak shift in the RL spectra is attributed to reabsorption. In order to investigate the relationship between that peak shift and the length of the path that the light travels in the dye solution, a further experiment is carried out.
In this case, a Rhodamine 6G (R6G; Sigma Alderich, Germany) water solution with a R6G concentration of 2×10-4 g ml−1 is used. The experiments are performed in a cuvette with the dimension of in width, length and height. The experimental setup is the same as shown in Fig. 1 (cuvette sample) with the exception that the spectra are measured from the bottom of the sample. Thus, a transmission measurement is performed: By varying the volume of the R6G solution inside the cuvette, the light path for the transmission can be altered which influences the reabsorption effect as well as the resulting peak shift of the fluorescence. Therefore, the relationship between peak shift and the total path length of the light in pure dye solution can be quantitatively described and will later serve as a reference for the relationship between the peak shift and the total path length of the light caused by the complicated multiple scattering in RL media.
2.3. Effect of scattering
This study uses Intralipid 20 % (IL; Fresenius Kabi, Germany) as scatterer. To be able to properly investigate the relationship between the RL emission spectra and the scattering properties of this substance, it is necessary to determine its scattering coefficient and anisotropy factor .
IL has already been extensively characterised in this respect, it is thus possible to rely on values from literature. [35–37] Generally, a distinction is made between dependent and independent scattering. For very low scatterer concentrations, dependent scattering may be neglected. However, as the scatterer concentrations in this study are in the low to high range, both types of scattering will be considered in order to minimise possible errors. Thus, Eq. (3) from Aernouts et al. [35] is applied to obtain values for the scattering coefficient of IL. In this Eq., the unit of is and the unit of is , is the concentration of IL and for an undiluted IL solution. In contrast, in the present study the concentration describes the fat concentration and the IL has a stock concentration of 22.67 % as volume concentration of scattering particles (soybean oil + egg lecithin). It should be noted that this difference is just a different definition of the concentration of IL, describing the same thing.
With the same reasoning, the anisotropy factor can be taken from literature as it also takes into account the dependent scattering. The g-factor is taken from Eq. (6) from Aernouts et al. [35]. For the wavelength range relevant in this study, this results in a value of . This value is provided approximately as it depends on the wavelength as well as on the concentration of IL. Nevertheless, this value shows that the scattering coefficient is four times higher than the reduced scattering coefficient. Hence, the difference is clear and high enough to see if an effect depends on the scattering coefficient or the reduced scattering coefficient.
In this study, the sample is a diffusive phantom consisting of distilled water, R6G as fluorescent dye and IL as a scatterer. The concentration of R6G is evaluated at 2×10-4 g ml−1. The used scatterer concentrations () are shown in Table 1 with the associated scattering coefficients . The scattering coefficients are taken from the study from Aernouts et al. [35]. As the wavelength of the RL varies, the central wavelengths for high pump energies are averaged and the scattering coefficients are then deduced from these means. For each scatterer concentration and each pump energy, five measurements are conducted.
Table 1. Concentrations of IL and the scattering coefficient according to Aernouts et al. [35] calculated for the averaged peak wavelength () of the RL.
| in % | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| in | 60 | 113 | 163 | 209 | 251 | 288 | 326 | 359 | 390 | 416 | 443 | 469 | 487 | 507 | 522 |
| in nm | 565 | 569 | 572 | 574 | 576 | 579 | 579 | 580 | 581 | 582 | 582 | 581 | 582 | 583 | 584 |
As the wavelength of the RL varies, these values are not exact - nevertheless, this error is less than a few percent and thus acceptable.
2.4. Theoretical considerations on the RL spectrum
In general, the spectrum of a laser can be described by a Gaussian or a Lorentzian function. The RL in this study can be described by the latter one.
The Lorentz distribution is defined as
| (1) |
where is the a parameter relating to the peak intensity, is a scale parameter with being equal to the full width at half maximum (FWHM) of the spectrum and is the central wavelength. For low concentrations of scatterers, the peak of the RL emission spectra is expected to be close to due to the fact that R6G has its fluorescence peak in water at around for the used concentrations of R6G. [38].
The RL is pumped by a large spot with a diameter of with a nanosecond laser in liquid media. Thus, most of the RL emission is incoherent or at least the RL emission is described as the sum of such large amount of coherent modes that they appear incoherent. Thus, the previous description is valid. From the fact that the RL will be mostly incoherent, it can be concluded that the three parameters in Eq. (1) describe the RL completely: peak wavelength, FWHM and maximum intensity. In this study, these three parameters are evaluated as a function of the scatterer concentration and the pump energy.
For further considerations, it is necessary to write the Lorentz distribution as a function of the wavenumber with . In this case, it reads as
| (2) |
where is a scale parameter with being equal to the FWHM of the spectrum and is the central wavenumber.
In the introduction of this study, it was already pointed out that human tissue can be used as RL. In the corresponding publications, a Fourier transformation (FT) of the RL emission spectrum was carried out and it was shown that peaks in the FT spectrum could be associated with characteristic quantities (i.e. the size of the cells) of the human material. It was thus found that these peaks in the FT spectrum represent the RL cavity sizes. [24,39]
As a square-integrable function, it is possible to Fourier transform the Lorentz distribution as
| (3) |
where is the cavity size. For further considerations, only the absolute value of Eq. (3) is important, being
| (4) |
As described above, the peaks of the FT function have already been taken into account - however, the general course of this exponential function, i.e. the course without the peaks, has not been considered. So far in the literature, it was only investigated if certain feature sizes are represented in the FT. In this study, it is assumed that the FT represents the complete cavity size distribution of the RL.
In this study, it is now hypothesised that the coefficient () of the Fourier transformed function reflects the distribution of the RL cavity sizes which is named the cavity size distribution. While the FT provides the cavity size distribution, the use of R6G complicates the matter. On the one hand, it allows the measurement of the total path length due to reabsorption of the RL light. On the other hand, the reabsorption effect of the lasing light might also influence the cavity size of the RL. Namely, this means that it is assumed that the coefficient for the cavity size distribution is influenced by the scattering lengths of the medium and reabsorption of the RL light.
This explanation allows to characterize if the presented method measures the scattering or the reduced scattering coefficient: It is necessary to examine under which of the following conditions the RL changes. Is it
| (5) |
or
| (6) |
3. Results
First, calibration results are shown that make it possible to relate the peak position of the RL to the path total length that the light has travelled in the dye solution. Afterwards, the results regarding the parameters , and are presented.
3.1. Relationship between RL peak position and total path length
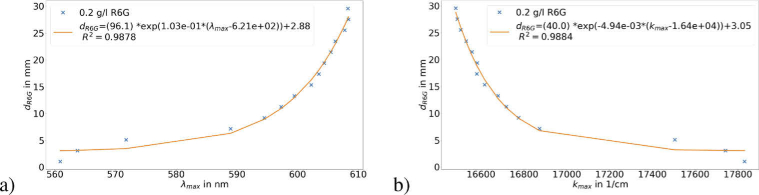
Figure 2 shows the shift of the peak wavelength () and the peak wavenumber (), respectively, as a function of the thickness of the R6G dye solution in the cuvette (). In general, the larger the thickness, the larger the shift is. For higher thicknesses, the change in the shift becomes smaller. From the fitting equations, the total path length (in mm) in the RL media can be directly calculated for a given RL peak wavelength (in ) or for a given RL peak wavenumber (in ).
Fig. 2.
Peak shift of the fluorescence of R6G in transmission measurement for different sample thicknesses. For this study, it is essential to know the thickness for a given peak shift. The x-axis is given in wavelength representation (a) or wavenumber representation (b); in both cases, the y-axis shows the thickness of the fluorescing media.
3.2. Effect of the scattering coefficient on the incoherent RL
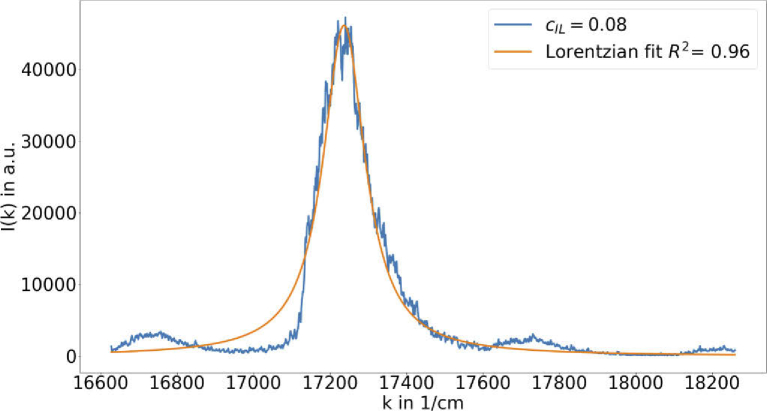
This section describes the experimental results based on the three fitting parameters from the Lorentzian function in Eq. (2) and how they are effected by the alteration of the scattering coefficient of the substrate. Figure 3 shows a typical RL spectrum with its related fit. The following three parameters are presented and discussed: Peak intensity (), width of the RL () and peak shift ().
Fig. 3.
Example of a RL spectrum with a pulse energy of 40.9 mJ for an scatterer concentration of 8 %. The orange spectrum is the fitted Lorentzian according to Eq. (2).
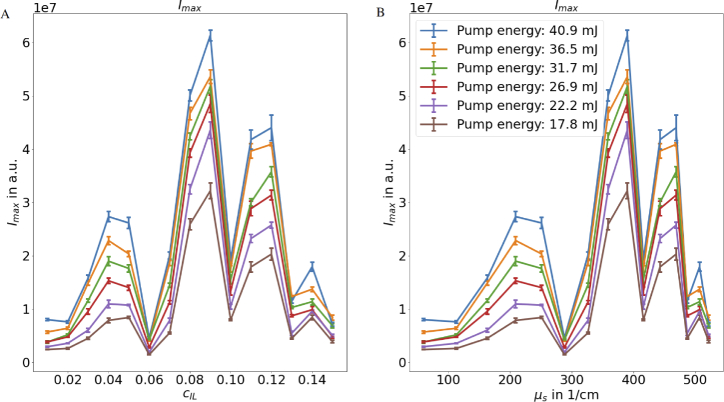
Peak intensity (): Figure 4 shows the maximum intensity () in for different scatterer concentrations. It can be seen that there is no monotonous behaviour. There are dips at scatterer concentrations of around , and corresponding to a scattering coefficient of , and , respectively. This clearly pinpoints that there are different RL regimes depending on the scatterer concentration. A similar finding could be described by Beckering et al. [22]: For a specific scatterer concentration the intensity of their RL peaked. However in their study, Beckering et al. [22] only did a coarse parameter scan. Hence, the intensity structure as a function of the scattering found in this study was most likely missed.
Fig. 4.
Maximum intensity () in for different scatterer concentrations (A) and scattering coefficients (B). The error bars represent the uncertainty of the mean value.
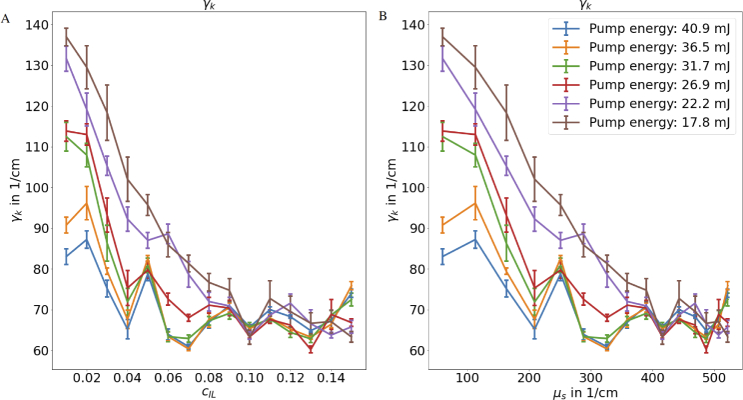
Width of the RL (): Figure 5 shows the width of the RL () in cm−1 for different scatterer concentrations. When looking at the corresponding graphs in the results section of this study and taking the pump energy into account, two phenomena become apparent: First, is significantly larger for low concentrations of the scatterer than for high concentrations of the same one. Second, seems to plateau around and .
Fig. 5.
Width of the RL () in cm−1 for different scatterer concentrations (A) and scattering coefficients (B). The error bars represent the uncertainty of the mean value.
The first effect can be explained by the stability of the RL, which increases with higher concentrations of scatterers. A higher concentration leads to a lower lasing threshold of the RL, meaning that a RL with the same pump energy is, depending on the scatterer concentration, differently far above the threshold. Thus, the lasing is stronger and, therefore, is smaller. Furthermore, the standard error decreases as well for higher scatterer concentrations. According to the Lévy distribution, a pump energy well above the threshold results in a less fluctuating stable lasing behaviour. Therefore, also the standard error of the mean is lower for higher scatterer concentrations and higher pump energies.
The parameter has a minimum between and for most IL concentrations at high enough pump energies. This corresponds to a resonator size distribution of of to according to Eq. (4). This can be compared to Eq. (5) and (6). Thereby, Eq. (5) does not play a role as is too small to be of importance due to the fact that as mentioned above. Again, a similar behaviour was found by Beckering et al. [22] without the fine resolution as in this study.
At the same time, the peak intensity reaches its maximum at a scattering coefficient of the substrate of around . Thus, it is likely that the resonator size distribution matches perfectly to the scattering size distribution. Hence, the RL is much stronger. Moreover at a scattering coefficient around , there is another maximum of the intensity. This corresponds to half the scattering coefficient of the previous maximum. Hence, it might be a harmonic as the resonator size distribution is half the size of the scattering size distribution. Therefore, it can be seen that the RL seems to interact mainly with the scattering length and not with the reduced scattering length. Thus, in conclusion, it is likely that the RL is usable to measure the scattering coefficient. However, it should be noted that this results is in contrast to the result from Tommasi et al. [15]. Nevertheless in their study, they separated the scattering from the gain medium. Furthermore, they derive their scattering information by measuring the peak intensity. In the study from Tommasi et al. [15], the scattering media seems to act more as a mirror due to the separation of the active medium and the scattering medium: The higher the scattering, the more light is back reflected into the probe. Hence, the peak intensity becomes higher. Thus, their setup measures the reduced scattering coefficient (). In this study, the scattering size distribution plays a major role as well as the RL modes. For this reason, the effect of the scattering coefficient () should dominate.
Again, there are some effects at scatterer concentrations of around , and corresponding to a scattering coefficient of , and , respectively. Thus, it is likely that this effect describes different RL regimes.
Peak shift (): Figure 6 shows the peak shift () in cm−1 for different scatterer concentrations. Examining the peak wavelength change of the RL emission spectrum as a function of the concentration of the scatterer, it is noticeable that this peak initially shifts towards longer wavelengths (lower wavenumbers) as the concentration increases, until from a certain concentration on the shift plateaus. This redshift in wavelength is in accordance with literature and happens due to the longer propagation path length of the light within the phantom. [22,32,34] It is also important that the peak shift is barely influenced by the pump energy. Especially for the higher pump energies, there is no influence on the peak shift. Hence, the peak shift is a parameter suited for the measurement of the scattering coefficient. Especially for IL concentrations up to 10 %, the effect of the pump power saturates for stronger pump powers. For these IL concentrations, the effect of the pump power is within the range of the measurement noise. That is why the effect of the pump power can be neglected in this region.
Fig. 6.
Peak shift () in cm−1 for different scatterer concentrations (A) and scattering coefficients (B). The error bars represent the uncertainty of the mean value.
Moreover, the same three regimes of the RL can be seen as for the other two parameters. Again, there are some effects at scatterer concentrations of around , and corresponding to a scattering coefficient of , and , respectively.
For the first two regimes, estimating the scattering coefficient is possible. For the third regime, the change is too small and not consistent. Furthermore, it can be concluded that the total path length () of the light increases up to the point where the scattering size distribution is identical to the resonator size distribution.
4. Discussion
The present study raises two main findings that need to be discussed. There is, first, the behaviour of the RL with its clear regimes and, second, the ability of the RL to measure the scattering coefficient.
In general, the resonator size distribution is nearly constant for high pump energies above a scattering coefficient of . At the same time, the total path length increases further which can be seen by the persistent red shift of the peak wavelength. This effect can have three possible consequences: First, the light can travel around the cavity more often. This is seen as unlikely, since the population inversion in a region should be depleted after a certain amount of round trips. Second, the overall cavity can become larger. Thus, there are more scattering events within the same cavity size distribution. This might be possible. However as this is a nano second RL in a liquid, Brownian motion most likely plays a role. This might prevent larger cavities. Third, the number of cavities may increase while the size of a single cavity remains constant. This case is the most likely one because the path generated by an average cavity size of only a few micrometres is not sufficient to produce the redshift obtained. Thus, the number of cavities is likely to increase. In short: The cavity of a RL is very small. If the concentration of the scatterer is increased, the number of available path lengths with an optimal size seems to rise in the medium. As a consequence, the light remains in the medium for a longer time.
Moreover, there seems to be an optimal resonator size distribution to which of the RL plateaus. This resonator size distribution happens at around to according to Eq. (4). A harmonics seems to appear at a resonator size distribution of around , while at a resonator size distribution of around , there is a minimum of the peak intensity. Furthermore, a higher scattering coefficient can lead to a weaker RL as a level is reached at which the light begins to less frequently reach those particles that contribute to optimal cavity sizes as other particles are interfering. This effect can be seen due to the reduction of the maximum intensity of the RL for scattering coefficients above . In other words, the cavity length is larger than the scattering mean free path. Thus, the emerging cavities are smaller than the optimal cavities of the RL. Hence, fewer appropriate cavities are available as a result, and the redshift stops. Interestingly, this effect reduces for even higher scattering. However, this cannot be explained currently.
In terms of the RL model introduced, it is useful to take the cavity size of the RL, the total path length and the scattering length of the medium into account. Since the RL is strongest when the cavity length is on the order of and not , this is a potent evidence that it is possible to directly determine the scattering coefficient with the RL. This works for scatterer concentrations up to that point where the scattering length is similar to the resonator size.
However, it should be noted that all experiments are done with one concentration of R6G of . Therefore, this R6G concentration has to be chosen for the for the application of the results. The reconstruction of the scattering coefficient would not work with other R6G concentrations as different R6G concentrations lead to different peak shifts. Hence, this is a drawback for the presented method if it is used for unknown samples. In this case, the R6G concentration has to be measured. Another factor which might influence the result is the spot size of the laser. However, experiments show that larger spot sizes of a factor of up to five only lead to a maximal change of the peak wavelength of 1 . Hence, this does not strongly influence the results. The last factor which influences the results is the size of the sample due to potential boundary effects. For high concentrations of IL, the total path length is up to around 0.7 . With the effect that the mode might not be generated in the centre of the sample, the maximal distance from the centre where lasing might be present is estimated to be around 1 . Except for the surface, there is no further boundary in range. Thus, smaller samples might alter the peak shift. Thus, the condition of a semi-infinite medium is of importance and it is fulfilled in this study; smaller samples might alter the peak shift.
Moreover there is one limitation of the interpretation of the results: The model ignores the effects from stimulated Raman scattering (SRS) which might be present when R6G is used as a fluorescence dye [40]. This point is essential to be considered as other publications mistook the SRS for coherent RL feedback [41]. When the pump wavelength is 532 nm, the Raman peaks appear at 573.8 nm, 578.7 nm, 580.8 nm and 583.4 nm [41,42]. These lines appear for different solvents and scattering materials such as vesicular polymer films [40], Ag nanowires dispersed ethanol [41,43] or methanol [42] and nanoparticles dispersed ethanol or ethylene glycol colloids [44]. The SRS-peaks appear in this study also for the given wavelengths. However for the IL concentrations below 9 %, the peaks are fairly small, except for the concentration of 3 %. However, the SRS peaks have a much smaller area than the Lorentzian shaped spectrum. Thus, it is assumed that the SRS is not dominating. Furthermore, the process of fitting a Lorentzian reduces the effect of small peaks. Nevertheless, SRS might still have a significant influence and it might be underestimated in this study.
5. Conclusion
In summary, this study shows that it seems to be possible to measure the scattering coefficient with the help of the RL. For this, a new model of the RL is presented in which the resonator size distribution derived by the Fourier transformation of the spectra in wavenumbers is essential as it allows the description of the cavity size distribution of the coherent RL. Thereby, it can be shown that this model explains the RL behaviour correctly. To our understanding, this model provides novel key insights into the comprehension of the RL. However, this model is not yet complete as for example the effect of different R6G concentrations is not studied. Moreover, effects from SRS might play a role and they have to be studied more carefully in future when R6G is used as fluorescence dye for random lasing.
Funding
Deutsche Forschungsgemeinschaft10.13039/501100001659 (German Research Founbdation - DFG) (414732368); Erlangen Graduate School of Advanced Optical Technologies10.13039/501100007216 (SAOT) by the Bavarian State Ministry for Science and Art10.13039/501100004563.
Disclosures
The authors declare no conflicts of interest.
Data availability
Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.
References
- 1.Kim A., Wilson B. C., “Measurement of ex vivo and in vivo tissue optical properties: methods and theories,” in Optical-Thermal Response of Laser-Irradiated Tissue, (Springer, 2010), pp. 267–319. [Google Scholar]
- 2.Sharma S., Banerjee S., “Role of approximate phase functions in Monte Carlo simulation of light propagation in tissues,” J. Opt. A: Pure Appl. Opt. 5(3), 294–302 (2003). 10.1088/1464-4258/5/3/324 [DOI] [Google Scholar]
- 3.Mourant B., Hielscher B., “Influence of the scattering phase function on light transport measurements in turbid media performed with small source-detector separations,” Opt. Lett. 21(7), 546–548 (1996). 10.1364/OL.21.000546 [DOI] [PubMed] [Google Scholar]
- 4.Foschum F., Bergmann F., Kienle A., “Precise determination of the optical properties of turbid media using an optimized integrating sphere and advanced Monte Carlo simulations. part 1: theory,” Appl. Opt. 59(10), 3203–3215 (2020). 10.1364/AO.386011 [DOI] [PubMed] [Google Scholar]
- 5.Bergmann F., Foschum F., Zuber R., Kienle A., “Precise determination of the optical properties of turbid media using an optimized integrating sphere and advanced Monte Carlo simulations. part 2: experiments,” Appl. Opt. 59(10), 3216–3226 (2020). 10.1364/AO.385939 [DOI] [PubMed] [Google Scholar]
- 6.Prahl S. A., van Gemert M. J. C., Welch A. J., “Determining the optical properties of turbid media by using the adding-doubling method,” Appl. Opt. 32(4), 559–568 (1993). 10.1364/AO.32.000559 [DOI] [PubMed] [Google Scholar]
- 7.Prahl S. A., “Everything I think you should know about inverse adding-doubling,” (2011), https://omlc.org/software/iad/manual.pdf
- 8.Hammer M., Roggan A., Schweitzer D., Muller G., “Optical properties of ocular fundus tissues-an in vitro study using the double-integrating-sphere technique and inverse Monte Carlo simulation,” Phys. Med. Biol. 40(6), 963–978 (1995). 10.1088/0031-9155/40/6/001 [DOI] [PubMed] [Google Scholar]
- 9.Hohmann M., Lengenfelder B., Kanawade R., Klämpfl F., Douplik A., Albrecht H., “Measurement of optical properties of pig esophagus by using a modified spectrometer set-up,” J. Biophotonics 11(1), e201600187 (2018). 10.1002/jbio.201600187 [DOI] [PubMed] [Google Scholar]
- 10.Jacques S., “Optical properties of biological tissues: a review,” Phys. Med. Biol. 58(11), R37–R61 (2013). 10.1088/0031-9155/58/11/R37 [DOI] [PubMed] [Google Scholar]
- 11.Faber D. J., Van Der Meer F. J., Aalders M. C., van Leeuwen T. G., “Quantitative measurement of attenuation coefficients of weakly scattering media using optical coherence tomography,” Opt. Express 12(19), 4353–4365 (2004). 10.1364/OPEX.12.004353 [DOI] [PubMed] [Google Scholar]
- 12.Vermeer K., Mo J., Weda J., Lemij H., De Boer J., “Depth-resolved model-based reconstruction of attenuation coefficients in optical coherence tomography,” Biomed. Opt. Express 5(1), 322–337 (2014). 10.1364/BOE.5.000322 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Hohmann M., Lengenfelder B., Muhr D., Späth M., Hauptkorn M., Klämpfl F., Schmidt M., “Direct measurement of the scattering coefficient,” Biomed. Opt. Express 12(1), 320–335 (2021). 10.1364/BOE.410248 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ignesti E., Tommasi F., Fini L., Martelli F., Azzali N., Cavalieri S., “A new class of optical sensors: a random laser based device,” Sci. Rep. 6(1), 35225–6 (2016). 10.1038/srep35225 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Tommasi F., Ignesti E., Fini L., Martelli F., Cavalieri S., “Random laser based method for direct measurement of scattering properties,” Opt. Express 26(21), 27615–27627 (2018). 10.1364/OE.26.027615 [DOI] [PubMed] [Google Scholar]
- 16.Cao H., “Review on latest developments in random lasers with coherent feedback,” J. Phys. A: Math. Gen. 38(49), 10497–10535 (2005). 10.1088/0305-4470/38/49/004 [DOI] [Google Scholar]
- 17.Luan F., Gu B., Gomes A. S., Yong K.-T., Wen S., Prasad P. N., “Lasing in nanocomposite random media,” Nano Today 10(2), 168–192 (2015). 10.1016/j.nantod.2015.02.006 [DOI] [Google Scholar]
- 18.Williams G., Bayram S., Rand S., Hinklin T., Laine R., “Laser action in strongly scattering rare-earth-metal-doped dielectric nanophosphors,” Phys. Rev. A 65(1), 013807 (2001). 10.1103/PhysRevA.65.013807 [DOI] [Google Scholar]
- 19.Cao H., Zhao Y., Ho S., Seelig E., Wang Q., Chang R. P., “Random laser action in semiconductor powder,” Phys. Rev. Lett. 82(11), 2278–2281 (1999). 10.1103/PhysRevLett.82.2278 [DOI] [Google Scholar]
- 20.Tulek A., Polson R., Vardeny Z., “Naturally occurring resonators in random lasing of π-conjugated polymer films,” Nat. Phys. 6(4), 303–310 (2010). 10.1038/nphys1509 [DOI] [Google Scholar]
- 21.Firdaus K., Nakamura T., Adachi S., “Improved lasing characteristics of zno/organic-dye random laser,” Appl. Phys. Lett. 100(17), 171101 (2012). 10.1063/1.4705471 [DOI] [Google Scholar]
- 22.Beckering G., Zilker S., Haarer D., “Spectral measurements of the emission from highly scattering gain media,” Opt. Lett. 22(18), 1427–1429 (1997). 10.1364/OL.22.001427 [DOI] [PubMed] [Google Scholar]
- 23.Ferjani S., Barna V., De Luca A., Versace C., Strangi G., “Random lasing in freely suspended dye-doped nematic liquid crystals,” Opt. Lett. 33(6), 557–559 (2008). 10.1364/OL.33.000557 [DOI] [PubMed] [Google Scholar]
- 24.Polson R. C., Vardeny Z. V., “Random lasing in human tissues,” Appl. Phys. Lett. 85(7), 1289–1291 (2004). 10.1063/1.1782259 [DOI] [Google Scholar]
- 25.Siddique M., Yang L., Wang Q., Alfano R., “Mirrorless laser action from optically pumped dye-treated animal tissues,” Opt. Commun. 117(5-6), 475–479 (1995). 10.1016/0030-4018(95)00176-9 [DOI] [Google Scholar]
- 26.Wang C.-S., Chang T.-Y., Lin T.-Y., Chen Y.-F., “Biologically inspired flexible quasi-single-mode random laser: an integration of Pieris canidia butterfly wing and semiconductors,” Sci. Rep. 4(1), 6736 (2015). 10.1038/srep06736 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Zhang D., Kostovski G., Karnutsch C., Mitchell A., “Random lasing from dye doped polymer within biological source scatters: the Pomponia imperatorial cicada wing random nanostructures,” Org. Electron. 13(11), 2342–2345 (2012). 10.1016/j.orgel.2012.06.029 [DOI] [Google Scholar]
- 28.Song Q., Xu Z., Choi S. H., Sun X., Xiao S., Akkus O., Kim Y. L., “Detection of nanoscale structural changes in bone using random lasers,” Biomed. Opt. Express 1(5), 1401–1407 (2010). 10.1364/BOE.1.001401 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.El-Dardiry R. G., Lagendijk A., “Tuning random lasers by engineered absorption,” Appl. Phys. Lett. 98(16), 161106 (2011). 10.1063/1.3571452 [DOI] [Google Scholar]
- 30.Yi J., Feng G., Yang L., Yao K., Yang C., Song Y., Zhou S., “Behaviors of the rh6g random laser comprising solvents and scatterers with different refractive indices,” Opt. Commun. 285(24), 5276–5282 (2012). 10.1016/j.optcom.2012.06.094 [DOI] [Google Scholar]
- 31.Hohmann M., Dörner D., Mehari F., Chen C., Späth M., Müller S., Albrecht H., Klämpfl F., Schmidt M., “Investigation of random lasing as a feedback mechanism for tissue differentiation during laser surgery,” Biomed. Opt. Express 10(2), 807–816 (2019). 10.1364/BOE.10.000807 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Cao H., Xu J. Y., Ling Y., Burin A. L., Seeling E. W., Liu X., Chang R. P., “Random lasers with coherent feedback,” IEEE J. Sel. Top. Quantum Electron. 9(1), 111–119 (2003). 10.1109/JSTQE.2002.807975 [DOI] [Google Scholar]
- 33.Wang Y., Duan Z., Qiu Z., Zhang P., Wu J., Zhang D., Xiang T., “Random lasing in human tissues embedded with organic dyes for cancer diagnosis,” Sci. Rep. 7(1), 8385 (2017). 10.1038/s41598-017-08625-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Ahmed S. A., Zang Z.-W., Yoo K. M., Ali M., Alfano R., “Effect of multiple light scattering and self-absorption on the fluorescence and excitation spectra of dyes in random media,” Appl. Opt. 33(13), 2746–2750 (1994). 10.1364/AO.33.002746 [DOI] [PubMed] [Google Scholar]
- 35.Aernouts B., Van Beers R., Watté R., Lammertyn J., Saeys W., “Dependent scattering in intralipid® phantoms in the 600-1850 nm range,” Opt. Express 22(5), 6086–6098 (2014). 10.1364/OE.22.006086 [DOI] [PubMed] [Google Scholar]
- 36.Aernouts B., Zamora-Rojas E., Van Beers R., Watté R., Wang L., Tsuta M., Lammertyn J., Saeys W., “Supercontinuum laser based optical characterization of intralipid® phantoms in the 500-2250 nm range,” Opt. Express 21(26), 32450–32467 (2013). 10.1364/OE.21.032450 [DOI] [PubMed] [Google Scholar]
- 37.Di Ninni P., Martelli F., Zaccanti G., “Intralipid: towards a diffusive reference standard for optical tissue phantoms,” Phys. Med. Biol. 56(2), N21–N28 (2011). 10.1088/0031-9155/56/2/N01 [DOI] [PubMed] [Google Scholar]
- 38.Zehentbauer F. M., Moretto C., Stephen R., Thevar T., Gilchrist J. R., Pokrajac D., Richard K. L., Kiefer J., “Fluorescence spectroscopy of rhodamine 6g: concentration and solvent effects,” Spectrochim. Acta, Part A 121, 147–151 (2014). 10.1016/j.saa.2013.10.062 [DOI] [PubMed] [Google Scholar]
- 39.Polson R., Levina G., Vardeny Z., “Spectral analysis of polymer microring lasers,” Appl. Phys. Lett. 76(26), 3858–3860 (2000). 10.1063/1.126801 [DOI] [Google Scholar]
- 40.Yashchuk V. P., “Coupled effect of stimulated raman scattering and random lasing of dyes in multiple scattering medium,” Laser Phys. 25(7), 075702 (2015). 10.1088/1054-660X/25/7/075702 [DOI] [Google Scholar]
- 41.Sun Y., Wang Z., Shi X., Wang Y., Zhao X., Chen S., Shi J., Zhou J., Liu D., “Coherent plasmonic random laser pumped by nanosecond pulses far from the resonance peak of silver nanowires,” J. Opt. Soc. Am. B 30(9), 2523–2528 (2013). 10.1364/JOSAB.30.002523 [DOI] [Google Scholar]
- 42.Vieira A. M., Oliveira N. T. C., de Araújo C. B., Martins W. S., de Oliveira R. A., Reyna A. S., “Influence of the excitation light disorder on the spatial coherence in the stimulated raman scattering and random lasing coupled regime,” J. Phys. Chem. C 125(10), 5919–5926 (2021). 10.1021/acs.jpcc.1c00266 [DOI] [Google Scholar]
- 43.Shi X., Chang Q., Bian Y., Cui H., Wang Z., “Line width-tunable random laser based on manipulating plasmonic scattering,” ACS Photonics 6(9), 2245–2251 (2019). 10.1021/acsphotonics.9b00508 [DOI] [Google Scholar]
- 44.de Oliveira P. C., Santos W. Q., Oliveira I. N., Jacinto C., “Random laser and stimulated Raman scattering in liquid solutions of rhodamine dyes,” Laser Phys. Lett. 16(5), 055002 (2019). 10.1088/1612-202X/ab1269 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.