Estimates of locus coeruleus function with functional magnetic resonance imaging are influenced by localization approaches and the use of multi-echo data

Abstract

The locus coeruleus (LC) plays a central role in regulating human cognition, arousal, and autonomic states. Efforts to characterize the LC’s function in humans using functional magnetic resonance imaging have been hampered by its small size and location near a large source of noise, the fourth ventricle. We tested whether the ability to characterize LC function is improved by employing neuromelanin-T1 weighted images (nmT1) for LC localization and multi-echo functional magnetic resonance imaging (ME-fMRI) for estimating intrinsic functional connectivity (iFC). Analyses indicated that, relative to a probabilistic atlas, utilizing nmT1 images to individually localize the LC increases the specificity of seed time series and clusters in the iFC maps. When combined with independent components analysis (ME-ICA), ME-fMRI data provided significant improvements in the temporal signal to noise ratio and DVARS relative to denoised single echo data (1E-fMRI). The effects of acquiring nmT1 images and ME-fMRI data did not appear to only reflect increases in power: iFC maps for each approach overlapped only moderately. This is consistent with findings that ME-fMRI offers substantial advantages over 1E-fMRI acquisition and denoising. It also suggests that individually identifying LC with nmT1 scans is likely to reduce the influence of other nearby brainstem regions on estimates of LC function.

1. Introduction

The locus coeruleus (LC) is a pair of small, cylindrical nuclei located in the brainstem near the fourth ventricle (4V). As the main site for the synthesis of the neuromodulator norepinephrine (NE), the LC influences many aspects of cognition and autonomic regulation (e.g., Aston-Jones, Gonzalez, & Doran, 2007; Berridge & Waterhouse, 2003). Because of its small size and location, however, investigations of LC function in humans using functional magnetic resonance imaging (fMRI) face a unique set of challenges in confidently localizing and isolating signals associated with neural activity in the LC. This paper investigates the effectiveness of two data acquisition and processing approaches in mitigating those problems: neuromelanin-weighted T1 (nmT1) imaging to localize the LC in each individual (Sasaki et al., 2006) as well as multi-echo functional magnetic resonance imaging (ME-fMRI) to increase blood oxygen level dependent (BOLD) contrast and reduce non-BOLD artifacts (Kundu, Inati, Evans, Luh, & Bandettini, 2012). To do so, we characterize differences in estimates of the intrinsic functional connectivity (iFC) of the LC when these approaches are and are not used.

Accurately characterizing LC function is important because it has implications for our understanding of a wide range of cognitive processes and neuropsychological disorders. Despite its small size, the LC projects to most of the central nervous system, excluding the striatum (Jones & Moore, 1977; Jones & Yang, 1985; Samuels & Szabadi, 2008). It also contains sub-populations of cells that project to different regions of the brain, such as the brainstem, spinal cord, medial prefrontal cortex, hippocampus, septum, and amygdala (Chandler, Gao, & Waterhouse, 2014; Schwarz & Luo, 2015), and has particularly dense projections to sensory and motor regions (Loughlin, Foote, & Bloom, 1986; Schwarz & Luo, 2015). LC projections also show large amounts of branching along the anterior-posterior axis in the neocortex that may be driven by the shared function of target regions (Loughlin, Foote, & Fallon, 1982; Aston-Jones & Waterhouse, 2016). In turn, the LC receives input from the brainstem, hypothalamus, central nucleus of the amygdala, anterior cingulate cortex, and orbitofrontal cortex (Aston-Jones et al., 1991; Luppi, Aston-Jones, Akaoka, Chouvet, & Jouvet, 1995). This circuitry allows the LC to regulate autonomic states and task engagement to influence how neural systems respond to behaviorally relevant events (Aston-Jones, Rajkowski, & Cohen, 1999; Glennon et al., 2019; Greene, Bellgrove, Gill, & Robertson, 2009; Nieuwenhuis et al., 2007; Mohanty, Gitelman, Small, & Mesulam, 2008). Its activity may be reflected in pupil dilation (Larsen & Waters, 2018; Swallow, Jiang, & Riley, 2019).

Although the precise mechanisms by which LC activity accomplishes all this are still being investigated (Mather, Clewett, Sakaki, & Harley, 2016; Uematsu, Tan, & Johansen, 2015; Schwarz & Luo, 2015), NE modulates the signal-to-noise ratio in brain regions involved in perceptual processing, including ventral visual cortex (Berridge & Waterhouse, 2003; Foote, Freedman, & Oliver, 1975; Warren et al., 2016), promotes memory consolidation and retrieval (Sara, 2009; Grella et al., 2019; Swallow, Jiang, & Riley, 2019), and may influence the integration of networks across brain regions (Shine et al., 2016). The importance of the LC for basic cognitive processing has been further reinforced by findings that pathology in the LC is accompanied by a decline in cognitive performance (Mather & Harley, 2016).

1.1. Localizing human LC and measuring its neuromelanin content using MRI

Given the importance of the LC for cognitive and neural processing across the lifespan, a growing number of studies have begun to investigate its structure and function using MRI. However, the size and location of the LC nuclei pose unique challenges to identifying them in these scans. LC nuclei are located in the upper portion of the pons, have between 22,000 and 51,000 neurons depending on one’s age (Mann, Yates, & Hawkes, 1983; Mather & Harley, 2016), and range in size between 31,000 and 60,000 μm³ (Mouton, Pakkenberg, Gundersen, & Price, 1994), with a within-plane diameter of around 2.5 mm (Fernandes, Regala, Correia, Gonçalves-Ferreira, 2012). In standard T1-weighted images, the LC and surrounding regions appear relatively homogenous, making identification of voxels that contain the LC difficult. This is further exacerbated by its small size and variability in location (Keren, Lozar, Harris, Morgan, & Eckert, 2009).

To help address the localization problem, neuroimaging sequences have been developed that increase the contrast for regions containing neuromelanin (nmT1 imaging), a pigment found in the LC (Sasaki et al., 2006). Neuromelanin is an iron containing product of catecholamine synthesis that causes paramagnetic T1 shortening (Enochs et al., 1997; Sulzer et al., 2018; Wakamatsu, Tabuchi, Ojika, Zucca, Zecca, & Ito, 2015). These paramagnetic effects can be leveraged by nmT1 imaging to increase the contrast of neuromelanin containing voxels to allow for the visualization and localization of the LC in structural MRI scans (Keren et al., 2009). Because regions that contain more neuromelanin appear brighter in nmT1 images, it also provides an in vivo measure of the amount of neuromelanin in the LC (and the other neuromelanin containing region in the brainstem: substantia nigra) (e.g., Keren et al., 2009; Keren et al., 2015; Liu et al., 2019).

However, the majority of studies on LC function do not make use of nmT1 imaging to localize the LC. Instead, they rely either on previously published coordinates, probabilistic atlases (such as developed by Keren et al., 2009), or use exploratory whole-brain analyses (for a review, see Liu, Marijatta, Hämmerer, Acosta-Cabronero, Düzel, & Howard, 2017). But because the precise location and shape of a brain region can vary across individuals, defining regions of interest (ROIs) at the group level risks missing the region in a given individual and capturing signal from surrounding areas. This can result in group level ROIs producing less reliable findings than individually defined ROIs (e.g., Swallow, Braver, Snyder, Speer, & Zacks, 2003). Therefore, coordinates from other studies or probabilistic LC ROIs, while likely to capture the LC, may also capture other nearby brainstem structures such as the inferior colliculus, the nucleus incertus, or other parts of the ascending reticular activating system that also play a role in arousal, orienting, and learning (e.g., Ryan, Ma, Olucha-Bordonau, & Gundlach, 2011). Another method of localization at the individual level is fully-automated or semi-automated segmentation (e.g., Morris et al., 2020). These often involve custom, in-house algorithms, with no single algorithm in widespread use. In the current study, we therefore contrast manual identification of the LC at the individual level guided by established protocols (Tona et al., 2017) with a widely employed probabilistic atlas that characterizes LC at the group level.

Concerns about an ROI capturing activity of nearby anatomical regions or cerebrospinal fluid (CSF) signal are further exacerbated by a commonly employed data preprocessing step: spatial blurring. Though EPI data are inherently blurry due to voxel size, spatial correlation, and motion (Scheinost, Papademetris, & Constable, 2014), pre-processing often employs additional blurring to reduce the effects of noise by averaging over nearby voxels. It also increases the likelihood that the ROI includes the signal of interest (Mikl et al., 2008). However, for small regions like the LC, blurring with a typical kernel may inadvertently reduce one’s ability to detect its activity. This is particularly problematic for regions, like the LC, that are close to large sources of physiological noise or changes in tissue. In these cases, blurring may introduce additional physiological noise into the signal unless measures are taken to preclude this possibility (e.g., by removing voxels from the fourth ventricle prior to blurring). When it comes to investigations of the LC, data blurring has also varied widely across studies (Liu et al., 2017) and there has been no systematic investigation of whether blurring, even by modest amounts, alters estimates of LC function and connectivity.

1.2. Estimating LC activity: multi-echo versus single-echo functional MRI

Previous investigations of LC function have used single-echo functional magnetic resonance imaging (1E-fMRI), which measures the MR signal in each voxel once per volume acquisition. By measuring the MR signal two or more times per acquisition, multi-echo (ME) fMRI offers two potential advantages over 1E-fMRI that could be particularly effective at reducing the impacts of non-BOLD noise and signal drop-out on estimates of LC function: maximization of BOLD contrast through the optimal combination of echoes during data analysis and independent components analysis (ICA) denoising.

With 1E-fMRI, the time at which the signal is measured (echo time; TE) is selected to maximize BOLD contrast for the brain as a whole, balancing variability in the susceptibility-weighted transverse relaxation (T2*) signal decay rates across the brain that arise from regional differences in tissue composition and signal drop-out (e.g., Cho & Ro, 1992; Park, Ro, & Cho, 1988). Because ME-fMRI measures the MR signal at multiple points during each acquisition, it can be used to estimate initial signal intensity and the rate at which the T2* signal decays at every voxel in the volume. This information can be used to create volumes that optimally weigh and combine the TEs for each individual voxel. Rather than choosing one TE for the entire brain, ME-fMRI can be used to effectively estimate the signal at the optimal TE for a given voxel and brain region after the data have been acquired (Kundu, Voon, Balchandani, Lombardo, Poser, & Bandettini, 2017). This approach has been used to improve BOLD contrast in regions of the brain that are subject to signal-dropout in typical 1E-fMRI, such as the ventromedial prefrontal cortex and nucleus basalis, without sacrificing contrast in other brain regions (Markello, Spreng, Luh, Anderson, & De Rosa, 2018).

Estimation of initial signal intensity and T2* decay also affords ME-fMRI data with a theoretically motivated approach to denoising BOLD data. Changes in BOLD activity are dependent on the TE, while artifactual effects on MR signal are TE-independent, and these can be algorithmically distinguished from each other (Kundu et al., 2012; Kundu et al., 2013). ME independent components analysis (ME-ICA) leverages these differences in order to identify and remove the contributions of non-BOLD signal components, such as head motion and physiological noise, from the data. Advantages of this process are that it is fully automated and requires no physiological measures, temporal noise models, or anatomical templates. It has been shown to significantly reduce the effects of head motion and other noise sources on BOLD data (Power et al., 2018). In contrast, denoising of 1E-fMRI data often requires removing observations that are likely to be contaminated by motion (e.g., by scrubbing) or by estimating and regressing out noise from motion and physiology (e.g., Dipasquale et al., 2017). For example, with RETROICOR, variance associated with cardiac phase and respiration is removed from the data using regression (Glover, Li, & Ress, 2000). Other approaches (e.g., ANATICOR; Jo, Saad, Simmons, Milbury, & Cox, 2010) estimate non-neural contributions to the BOLD signal by regressing out signal captured in nearby white matter voxels or CSF. Principle components and independent components analysis can also be used, for example, to identify and remove motion related components (e.g., ICA-AROMA; Pruim, Mennes, Van Rooij, Llera, Buitelaar, & Beckmann, 2015). These methods are sometimes employed in conjunction with the inclusion of first- and second-order motion regressors in the statistical analyses. However, when directly compared to ME-ICA, these methods have been shown to be less effective at reducing noise, reflected in ME-ICA’s greater temporal signal to noise ratio (tSNR) and lower spatial standard deviation of successive difference images (DVARS; Lombardo et al., 2016; Markello et al., 2018; Dipasquale et al., 2017). Nevertheless, they may offer good alternatives to ME-fMRI if only 1E-fMRI acquisition is possible.

Previous studies investigating the iFC of the LC have not consistently accounted for cardiac and respiratory effects, and few have reported correcting for motion (Liu et al., 2017). For example, Murphy, O’Connell, O’Sullivan, Robertson, & Balsters (2014) explicitly report applying RETROICOR. Krebs, Park, Bombeke, & Boehler (2018) did not have physiological recordings for denoising. Instead, they compared activity in the LC to neighboring regions and concluded that LC activity in their data was not primarily driven by physiological noise. Because physiological and motion-related noise can cause spurious correlations in iFC maps (Power et al., 2012), steps to reduce their impact on the data are needed to gain a better understanding of LC function. This is particularly important for the LC because of its size and location near the 4V and increased likelihood that it will contain signals from CSF. In fact, previous neuroimaging studies showing task-related activity in the vicinity of the LC have been called into question precisely because of this problem (Astafiev, Snyder, Shulman, & Corbetta, 2010).

A previous investigation of the use of ME-ICA with a pair of small brain regions in the human basal forebrain, the nucleus basalis of Meynert and the medial septum (Markello et al., 2018), suggest that ME-ICA may also provide significant advantages over 1E-fMRI approaches when investigating the iFC of the LC. Like the nucleus basalis of Meynert and the medial septum, the small size and location of the LC near the boundary between tissue and CSF make it particularly important to account for signal dropout from local field inhomogeneities and to remove noise from non-neural sources. Therefore, to investigate whether ME-fMRI offers a benefit above and beyond traditional single-echo scans, this study examines differences in the estimated functional characteristics of the LC when using ME-fMRI relative to 1E-fMRI.

1.3. The current study

Human neuroimaging of the LC has been hampered by several related issues: localizing the LC, isolating LC activity from other nearby regions, and removing the effects of noise from motion and physiology. In this study, we investigate whether using nmT1 images, ME-fMRI, and conservative amounts of data blurring can offer appreciable advantages to one’s efforts to characterize LC function.

Previous work on ME-ICA and small brain regions like the nucleus basalis of Meynert suggests we should also see appreciable gains in signal-to-noise ratio of imaging data of the LC. To investigate those effects of ME-fMRI, our main analyses compared a pipeline that utilized all three echoes from an ME-fMRI acquisition to a pipeline that utilized only the second echo (E2) from the same acquisition. Because both pipelines utilized data from the same run, this approach held state dependent brain activity constant and minimized concerns about inter-run reliability (Birn et al., 2013). Additional data and analyses comparing data acquired in a 1E-fMRI scan to data from a second ME-fMRI scan are presented in the Supplemental Materials. These include a brief analysis of pupillometry data acquired in the same participants.

Although nmT1-based localization could result in better specificity of the extracted LC timeseries, it is unclear to what extent this would affect subsequent characterization of LC function compared to more time efficient atlas-based approaches. To help answer this question, we also briefly describe a method for standardizing nmT1 signal intensity using the whole brainstem, as previously reported approaches are inconsistent in their use of a reference region. Intrinsic functional connectivity analyses of resting state data formed the basis for comparing these different approaches (Biswal, Yetkin, Haughton, & Hyde, 1995; Van den Heuvel & Hulshoff Pol, 2010). Although previous studies have characterized iFC of the LC using resting state data (e.g. Murphy et al., 2014; Song et al., 2017; Zhang, Hu, Chao, & Li, 2016), there is little published data investigating the impact of different methodological and analytical approaches on estimates of LC function (but for a review of approaches used, see Liu et al., 2017). The current paper meets this need and suggests that different localization, data acquisition, and denoising approaches can lead to substantially different characterizations of LC function and connectivity.

2. Methods

2.1. Participants

A total of 20 right-handed participants (14 female, 6 male; 19–40 years old, M = 21.05, SD = 4.57) completed one multi-echo resting state run. Participants were screened for non-MRI compatible medical devices or body modifications (e.g., piercings, implants), claustrophobia, movement disorders, pregnancy, mental illness, use of medication affecting cognition, and color blindness. All participants provided consent at the start of the session, were debriefed at the end, and all procedures were approved by the Cornell University Institutional Review Board.

2.2. MRI Acquisition

Magnetic resonance imaging was performed with a 3T GE Discovery MR750 MRI scanner and a 32-channel head coil at the Cornell Magnetic Resonance Imaging Facility in Ithaca, NY. Participants laid supine on the scanner bed with their head supported and immobilized. Ear plugs, headphones, and a microphone were used to reduce scanner noise, allow the participant to communicate with the experimenters, and to present auditory stimuli during the tasks. Visual stimuli were presented with a 32” Nordic Neuro Lab liquid crystal display (1920 × 1080 pixels, 60 Hz, 6.5 ms g to g) located at the back of the scanner bore and viewed through a mirror attached to the head coil. Pulse oximetry and respiration were recorded throughout all scans.

Anatomical data were acquired with a T1-weighted MPRAGE sequence (TR = 7.7 ms; TE = 3.42 ms; 7° flip angle; 1.0 mm isotropic voxels, 176 slices). A second anatomical scan utilized a neuromelanin sensitive T1-weighted partial volume turbo spin echo (nmT1) sequence (TR = 700 ms; TE = 13 ms; 120° flip angle; 0.43 × 0.43 mm in-plane voxels, 10 interleaved 3.0 mm thick axial slices, 0 mm spacing; adapted from Keren et al., 2009). Slices for the nmT1 volume were oriented per-pendicular to the brain stem to provide high resolution data in the axial plane, where the dimensions of the LC are smallest, and positioned to cover the most rostral portion of the pons.

Participants completed one resting state scan with eyes open and the lights on during multi-echo echo planar imaging (612s; TR = 3.0 s; TEs = 13, 30, 47 ms; 83° flip angle; 3.0 mm isotropic voxels; 46 interleaved slices). The display was set to a uniform light grey background throughout the scan. Participants were told to keep their eyes open and remain awake throughout the scan, but were free to move their eyes and blink as needed. Eye movements, blinks, and pupil size were recorded with an Eyelink 1000 Plus MRI Compatible eye tracker (SR-Research, Ottawa, Ontario, Canada). However, because participants were free to blink and move their eyes as needed, the recordings were too noisy to analyze with confidence. A second set of data with higher quality pupillometric measures is reported in the Supplemental Materials for those interested. Participants subsequently completed additional scans that will be reported separately.

2.3. Region of Interest Identification

2.3.1. Anatomically Defined Regions

Anatomical data were submitted to FreeSurfer’s segmentation and surface-based reconstruction software (recon-all; v 5.3; http://surfer.nmr.mgh.harvard.edu/; Dale, Fischl, & Sereno, 1999; Fischl, Sereno, & Dale, 1999) to label each individual’s anatomy. Labels for cortical gray matter (GM), ventral medial prefrontal cortex (vmPFC), fourth ventricle (4V), hippocampus (HPC), primary visual cortex (V1), brainstem, precentral gyrus (motor cortex, MC), and transverse temporal gyrus (auditory cortex, AC) were extracted and converted to volumetric ROIs using FreeSurfer and AFNI (Cox, 1996) tools. A white matter (WM) ROI was similarly created, but eroded using AFNI’s 3dmask_tool (dilate_input −2) to ensure that the ROI did not extend into nearby regions.

2.3.2. Locus Coeruleus

Voxels that were likely to include the locus coeruleus were identified in two ways: using the probabilistic Keren atlas and using individual nmT1 images. ROIs that were based on the Keren atlas were defined using the binary 1 SD and 2 SD masks, provided by those authors (referred to here as K1 and K2 ROIs, respectively; Keren et al., 2009) in the MNI152 atlas (T1 MNI-152 0.5 mm iso-voxel). To provide the most conservative comparison between the Keren atlas and the nmT1-based LC ROIs, analyses focused primarily on the K1 ROI. The Keren atlas is based on nmT1 images (3 × 0.4 × 0.4 mm axial slices) of 44, righthanded, healthy adults, aged 19–79. Their final probabilistic atlas was based on the group means and standard deviations of the highest intensity voxels on the left and right in each axial slice (for more details, see Keren et al., 2009).

Individual, hand-traced LC ROIs (referred to as LC ROI from here on) for each participant were defined using the nmT1 image, with the same scanning parameters as used for the Keren atlas. Tracing was performed on the un-transformed nmT1 image to take advantage of its high in-plane resolution and to avoid blurring the data when aligning and resampling to the participant’s native MPRAGE. Prior to tracing the ROIs, the individual MPRAGE (with skull, for additional landmarks) and anatomical parcellation from Freesurfer were aligned to the nmT1 image using a 6 parameter affine transformation (AFNI’s align_epi_anat.py; Cox & Jesmanowicz, 1999; Saad, Glen, Beauchamp, Desai, & Cox, 2009). All non-brainstem and non-4V voxels were then masked from the nmT1 images. Each slice was mean centered by subtracting the mean signal intensity of voxels within the brainstem from all voxels in the slice (corrected nmT1 image).

The LC was manually defined in FreeView (https://surfer.nmr.mgh.harvard.edu) on the corrected nmT1 images by two independent raters (authors HBT and ER) using the following criteria (adapted from Tona et al., 2017; see Figure 1):

1. The corrected nmT1 image was viewed in false color and overlaid on the aligned MPRAGE image. Brush size was 1 voxel.

2. Visual contrast was equated across participants using a predefined range for the false color palette (Jet - minimum: 10, maximum: 80). Pixel intensity threshold for inclusion in the LC (only green, yellow, orange and red pixels could be included; values roughly ≥ 40) was agreed upon prior to drawing the ROIs.

3. Two landmarks were used to locate the most rostral portion of the LC: the lower boundary of the inferior colliculus (seen in sagittal view) and the upper boundary of the 4V (seen in axial view). The rostral end of the LC was in the first axial slice caudal to the inferior colliculus in which two distinct hyperintensities on the edge of the 4V were visible in the nmT1 image.

4. The LC was defined starting on this slice and moving caudally through the pons. Hyperintensities in more caudal slices were included in the LC only if they were both sufficiently bright and connected to hyperintensities in the next most rostral slice, verified in sagittal and coronal views.

5. Tracing was informed by the assumption that each LC nucleus would appear as a roughly circular shape within each axial slice, resulting in bilateral, roughly cylindrical regions. In addition, the LC was assumed to be solid and contain no holes. If a voxel was surrounded in-plane by voxels included in the LC, then that voxel was also included.

6. In some cases, a second, more medial hyperintensity was found near the rostral part of the LC. This region was taken to be part of the trochlear nerve and was not included in the LC ROI. Avoiding this secondary hyperintensity prevented the LC ROI from having a very oblong shape or extending to the midline at any point.

Fig. 1.

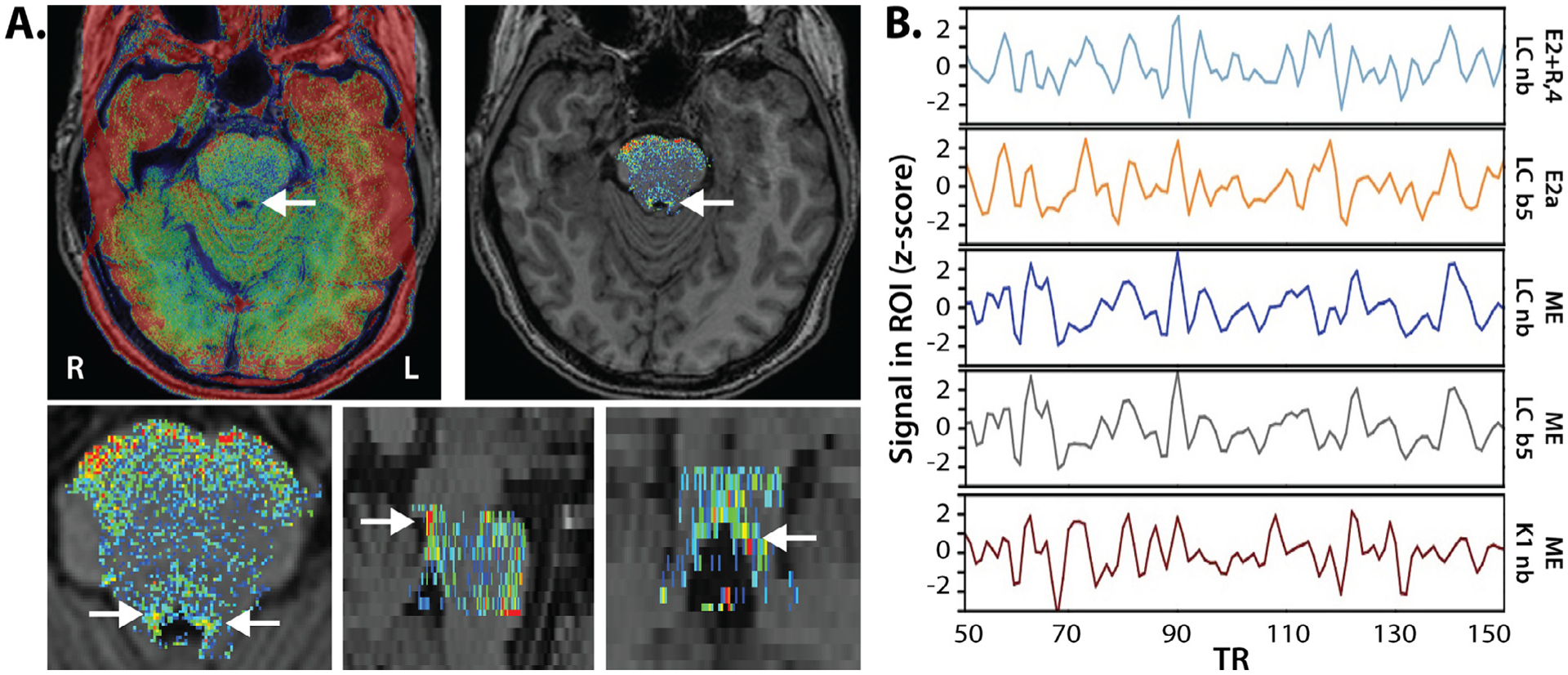
Visualization of the ROI creation and seed extraction process. A) Individual MPRAGE scans (including skull) were aligned to the normalized nmT1 image (arrow is pointing to LC; top left) to preserve the higher in-plane spatial resolution of the nmT1 images. After extracting the brainstem from the nmT1, correcting image intensity, and setting the false color palette to the predefined range (low values in blue, high values in red, range = 10–80), potential LC voxels can now be visually distinguished from nearby regions (top right). Two researchers independently traced the LC according to the protocol described in the methods, by selecting voxels that appeared yellow or redder (corresponding roughly to intensity values ≥ 40). Candidate voxels are visible in the axial, sagittal, and coronal plane (bottom row). B) Excerpts from one individual’s seed time series (acquisition numbers 50 to 150; z-scored) following different denoising pipelines. LC, K1, and K2 seeds were always extracted in native space. ME = multi-echo, ME-ICA denoised data; E2 + R,4 = second echo with RETROICOR and 4V regression; E2a = E2 pipeline including ICA-AROMA; LC = hand-traced LC ROI; K1 = 1 SD Keren ROI; nb = native blur data; b5 = data blurred to 5 mm FWHM.

An individual’s final LC ROI consisted of voxels included in both raters’ ROIs, after removing any voxels that overlapped with 4V. The 4V was defined starting from the most rostral axial slice in which the cerebral aqueduct began to widen, until the most caudal axial slice in which the ventricle appeared dark and had an inverted-U shape.

A probabilistic map illustrating the location and distribution of the LC ROIs in all participants was created by registering each person’s LC ROI to MNI152 space. To do so, alignment parameters were calculated for each individual by combining the inverse of the transformation that aligned the native MPRAGE and nmT1 images and the nonlinear transformation from the individual’s native MPRAGE to MNI152 standard calculated by 3dQwarp and then applied using 3dNwarpApply. Successful alignment of the brainstem to the individual MPRAGE and the MNI152 template was visually confirmed. Similar to previous findings (e.g., Tona et al., 2017), linear transformations were inadequate for registering a small brainstem ROI to the MNI152 space: with affine registration only, many LC ROIs overlapped the 4V or other parts of the pons. LC ROIs in MNI152 space were thresholded to remove scattered non-zero voxels introduced by the nonlinear warping process, by removing any voxels with values of 0.1 and below. Finally, each voxel value was divided by the number of participants to create the probabilistic map (Fig. 2).

Fig. 2.

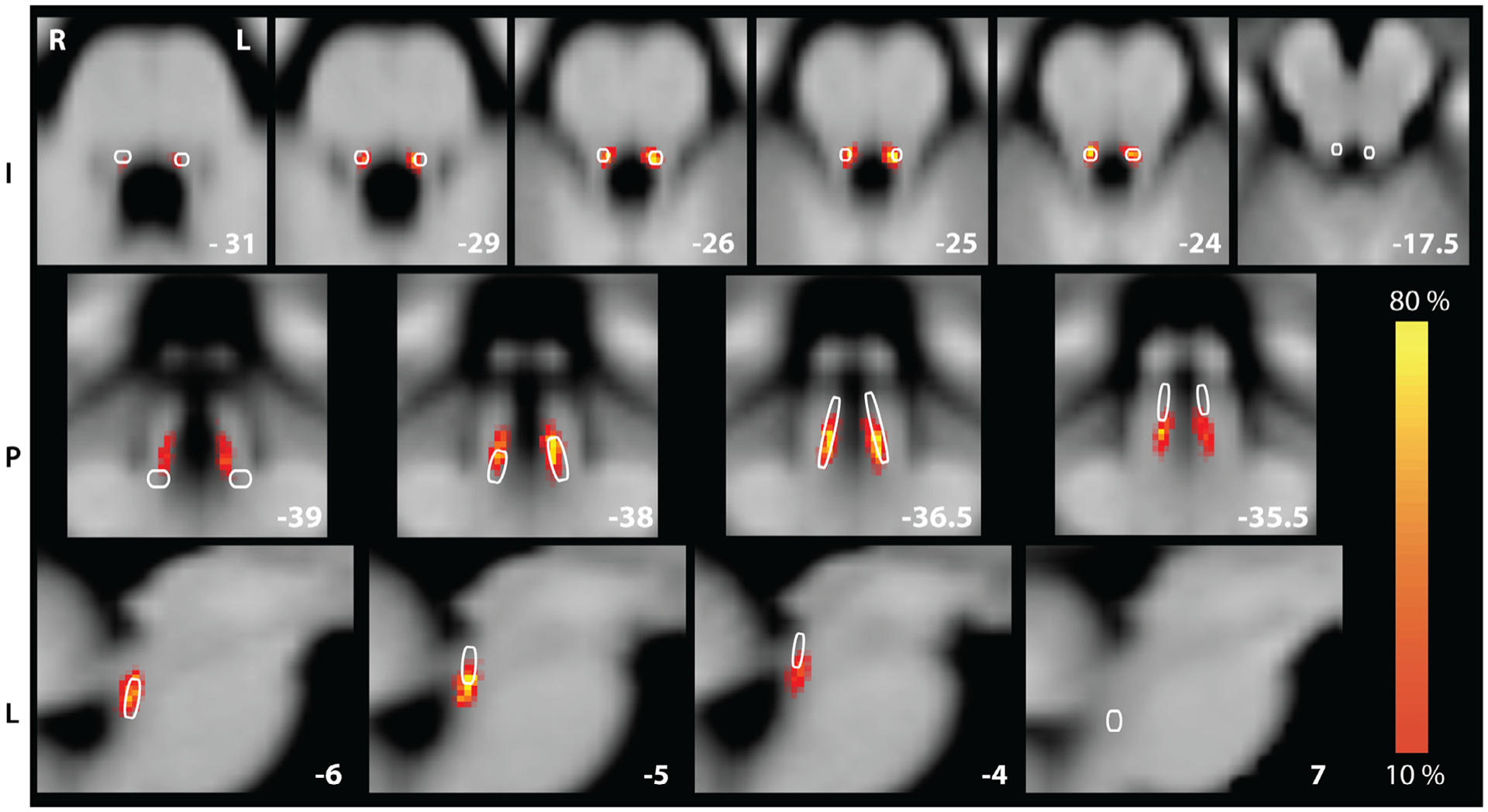
Hand-traced LC atlas (heat; percentage of participants in the long-TR dataset) and binary K1 atlas (white outline) in MNI152. Slices were selected to best visualize similarities and differences between the LC heat map and K1 ROI. This figure is for illustrative purposes only: each LC, K1, and K2 ROI was applied to functional data aligned to the individual’s native anatomy, but is being shown here aligned to MNI152 for aggregation and comparison to the Keren atlas as shown in Keren et al. (2009). Coordinates in LPI.

2.3.3. Pontine Tegmentum

Within axial slices of the participant’s MPRAGE (as aligned to the nmT1), the pontine tegmentum (PT) ROI was defined as a circular ROI 10 voxels in diameter centered at the midline of the brainstem, ventral to the fourth ventricle, and approximately equidistant from the left and right LC ROIs, to define the vertex of an equilateral triangle. The PT ROI was defined only in slices that also contained an LC ROI (see also Clewett, Lee, Greening, Ponzio, Margalit, & Mather, 2016).

2.3.4. Alignment of ROIs to Native Space

ROI statistics and seeds for time series and iFC analyses were acquired in native space after aligning the LC and PT ROIs (acquired in nmT1 space), the K1 and K2 ROIs (originally in MNI152 space), and functional data to the native MPRAGE for each individual. The LC and PT ROIs were aligned to native space by using the inverse of the transformation used to align the individual MPRAGE and nmT1 images. The K1 and K2 ROIs were transformed to each participant’s native space using the inverse of the 3dQwarp transformation between MNI152 and the participant’s native MPRAGE. They were then thresholded at 0.1 and resampled to the 3 mm isotropic grid. This approach minimized transformation of the EPI data and equated the number of transformations computed and applied to each of the ROIs.

2.4. LC Neuromelanin Intensity

To compare neuromelanin intensity across individuals, rescaling parameters were obtained from the corrected nmT1 image: the mean, standard deviation, a minimum value (min = M-3* SD), and a maximum value (max = M + 3*SD) were calculated using non-LC voxels from axial slices in which LC was defined. The minimum and maximum values were defined as M +/− 3 * SD from the mean to reduce the effects of extreme outliers that were present for all participants. Using these non-LC voxels, all voxels in the corrected nmT1 image were then rescaled using the equation $\frac{(x-min)}{(max-min)}$, resulting in an image with values that were referenced to the minimum intensity and unit scale equal to 6 standard deviations of the non-LC voxel signal intensities. The rescaled intensity values within the LC ROIs were then averaged to obtain the mean intensity for each participant. With this approach, LC intensity can be interpreted in terms of the range of non-LC nmT1 intensity values (e.g., a value of 2 indicates that the LC was twice as intense as the maximum of the non-LC values, relative to the minimum).

2.5. MRI Data Pre-processing

To evaluate the effects of different denoising procedures on data quality and the resulting iFC maps, five single-echo pre-processing pipelines and one multi-echo pre-processing pipeline were used. Pre-processing of ME data were modeled after the procedures outlined in Jo et al. (2013) and Markello et al. (2018). The E2 pipelines differed in amount and method of noise removal, but were otherwise matched as closely as possible to the ME pipeline. See Supplemental Materials for a flowchart illustrating all pipelines. We first describe the pipeline used for ME-ICA denoising, followed by the various E2 pipelines.

For the ME pipeline with ME-ICA-denoising, the standard ME-ICA pipeline (meica.py, Version 2.5, beta 9; tedana.py, Version 2.5 beta 9; t2smap.py, Version 2.5 beta 6; Kundu et al., 2012; Kundu et al., 2013) was implemented using the following steps. First, the MPRAGE volume was skull stripped using FSL BET (b = 0.25). Second, the obliquity of the anatomical volume was matched to the EPI time series. Third, motion was estimated using the first echo time series using 3dvolreg with the third volume as the target. The parameters for deobliqueing the data and calculating motion were saved for use during motion correction and volume registration in Step 7. Fourth, all EPI data were despiked and slice time acquisition differences were corrected using 3dTshift. Fifth, for each echo time series, the first two volumes were dropped and the remaining EPI data were registered to the third volume. Sixth, the three echoes were concatenated and processed by t2smap.py to generate the baseline intensity volume (s0), the T2* relaxation map, and the optimal combination volume time series (OCV). Seventh, the OCV was used to calculate coregistration parameters to the anatomical image. These coregistration parameters and the previously calculated deobliqueing parameters were then applied to the EPI data in one step to align the data with the individual anatomical volume in its original acquisition space. Eighth, EPI data were denoised using ME-ICA to identify and separate BOLD components from non-BOLD components (tedana.py; Kundu et al., 2012; Kundu et al., 2013). This approach identifies BOLD components based on quantifying the T2* portion of the BOLD fMRI signal (see Kundu et al., 2013 for a complete description). BOLD components were selected automatically by identifying components that showed TE-dependent decay. These components were then recombined with thermal noise, to create the denoised EPI data. Ninth, because global signal regression was not used, nuisance regressors capturing unaccounted for physiological and motion related noise (Power et al., 2018) (demeaned motion) were then obtained by averaging the time series of each voxel within the WM and 4V ROIs. All regressors were obtained prior to blurring the data (native blur; nb), to avoid further contaminating the regressor with signal from neighboring areas (Jo et al., 2013). Tenth, to examine the effects of blurring on the analyses, a second data set was created in which the data were incrementally blurred until the observed smoothness was 5mm FWHM and was uniform throughout the brain (b5; 3dBlurtoFWHM). Voxels from the 4V were masked during blurring. Eleventh, the nb and b5 data were bandpass filtered (0.01 < f < 0.1) and nuisance regressors were removed, in one step, with 3dTproject (cenmode NTRP). Bandpass filter thresholds were selected to reflect conventional values used in resting state analyses (e.g., Yan et al., 2013; Wu, Gu, Lu, Stein, Chen, & Yang, 2008; cf., Chen & Glover, 2015). Finally, alignment parameters to MNIa were computed using AFNI’s @auto_tlrc on the MPRAGE and then applied to the cleaned b5 data. Once in MNIa space, the cleaned and blurred EPI data were used as the target volume for iFC. The target volume was always a blurred dataset. A copy of the nb and b5 EPI was kept in native space to extract the LC, K1, and other ROI seeds.

E2 data were denoised in five different ways: four pipelines that were based on commonly used regression approaches (referred to collectively as regression-based denoising) and one that used ICA-AROMA (collectively referred to with ME-ICA as components-based denoising). Except where noted, these pipelines were matched to the ME pipeline described in the previous paragraph. For the E2 + basic pipeline, pre-processing skipped Steps 6 and 8, coregistration parameters were calculated using the E2 EPI data, and nuisance regressors included only WM signal, demeaned motion, and the first derivatives of the motion regressors. The E2 + R pipeline was the same as the E2 + basic pipeline with the addition of RETROICOR denoising between Steps 3 and 4: respiration and pulse oximetry data were used to generate per slice regressors using AFNI’s retroTS.py (Glover et al., 2000) and these were removed from the EPI data using 3dREMLfit. The E2 + 4 pipeline also was the same as the E2 + basic pipeline, but included the 4V time series as a nuisance regressor. The fourth pipeline, E2 + R,4, included RETROICOR and 4V regression, resulting in a typical regression-based denoising approach.

A final pipeline, E2a, introduced ICA-AROMA into the E2 + R,4 pipeline and used ICA to identify noise components, similar to ME-ICA, although for motion. For this pipeline, we adapted the procedure from Pruim et al. (2015) into the E2 + R,4 pipeline: linear registration parameters were computed with FSL-FLIRT and boundary-based registration (Jenkinson, Bannister, Brady, & Smith, 2002; Jenkinson & Smith, 2001; Greve & Fischl, 2009) and non-linear registration parameters with FSL-FNIRT (Andersson, Jenkinson, & Smith, 2007). Motion parameters were estimated with MCFLIRT (Jenkinson et al., 2002). This pipeline utilized blurred (b5) data exclusively, to keep it in line with the methods outlined in Pruim et al. (2015). Results with blurring at levels typically used with ICA-AROMA (6mm) can be found in the Supplemental Materials. After blurring, ICA-AROMA was performed with automatic component selection through MELODIC (Beckmann & Smith, 2004) and non-aggressive denoising. Because ICA-AROMA removes noise related to motion, motion parameters and their derivatives were not included as nuisance regressors in Step 11.

To examine the effects of blurring prior to seed extraction, we extracted the time series within the LC, K1, K2 and PT ROIs both before (nb) and after (b5) the data were blurred up to 5 mm FWHM for all pipelines except E2a. Thus, the blur indicator in all pipeline labels always refers to the blurring of the seed, not the target volume. Because blurring was performed using AFNI’s 3dBlurToFWHM, the smoothness of the data was increased until it was estimated to be 5 mm FWHM throughout the brain, rather than adding a specific amount of blurring on top of the existing native blur.

2.6. Intrinsic Functional Connectivity Analyses

For first level functional connectivity analyses, seeds were created by averaging the time series of voxels within the ROIs in native space. The seed time series were then correlated with the timeseries of each voxel in the blurred data set (b5) in MNIa space for visualization (note that nb or b5 in the pipeline name always refers to the seed, as the target volume for the iFC was always blurred to 5mm FWHM). The Fisher r-to-z transform was then applied to the correlation maps to produce z-maps for the second level analysis. In the second level analysis, voxel-wise t-tests (3dTtest ++) were performed to test each pipeline against zero and the statistical maps were controlled for multiple comparisons using the false discovery rate (FDR; Genovese, Lazar, & Nichols, 2002). First and second level analyses were performed for each of the denoised data sets to produce functional connectivity maps that varied along several factors: E2 vs. ME (data type), LC vs K1 seeds (ROI), and nb vs. b5 prior to seed extraction (blur).

2.7. Data and Code Availability Statement

Data from the studies reported in the main manuscript and the supplemental materials can be made available upon reasonable request and with proper approval from relevant research and ethics entities. Most analyses used publicly available software (AFNI, FSL, meica.py). Annotated analysis scripts for AFNI, FSL, MATLAB, Python, and R can be found on the GitHub of author HBT (https://github.com/HamidTurker).

3. Results

3.1. Summary of Comparisons and Analyses

The aforementioned procedures allowed us to examine the effects of several data acquisition or pre-processing choices on data quality and functional connectivity maps of putative LC regions. Analyses were carried out in several phases. First, we focused on assessing changes to tSNR and DVARS following various forms of E2 denoising and ME-ICA on ME-fMRI data. These analyses indicated that among the E2 pipelines, E2 + R,4 performed best in terms of tSNR and E2a performed best in terms of DVARS. ME-ICA was superior to both of these. We then assessed the specificity of the various seed time series that result from these three pipelines. Finally, we characterized the connectivity maps that result from those time series.

3.2. Locus coeruleus localization and intensity measurement

To characterize the location and reliability of the LC ROIs defined on the nmT1 images (indicated with the white arrow in Figure 1 A), we measured inter-rater agreement and inter-individual differences in LC size and location. The average Dice similarity coefficient between the raters’ ROIs was 0.81 (range 0.44–1.00). In MNI152 space, the average location of the center of mass of the right and left LC were (neurological coordinates Left-Posterior-Inferior) [LPI]: −5.26, 37.15, −25.91 and 3.67, 37.30, −26.36, respectively. The LC had an average total volume of 37.5 ± 11.8 mm ³, with an average length of 9.28 ± 2.28 mm. The volume of the left ROI was significantly larger than the right ROI (left volume 21.90 ± 7.14 mm ³, right volume 15.56 ± 5.43 mm ³, paired t-test, t(20) = 6.35, p < 0.001). The length did not differ significantly between the right and left ROIs. These values show good agreement with those of postmortem studies on “core” LC volume (German et al., 1998; Fernandes et al., 2012). In addition, the group-level heat map visually overlapped with the K1 ROI (Fig. 2), though the average Dice coefficient between the individual LC ROIs and the K1 ROI was low (M = .143, SD = .063, range = .011–255). Accordingly, the K1 ROI consisted of different, and more, voxels than the individual LC ROIs. LC intensity was standardized across participants using the mean and standard deviation of non-LC voxels within the brainstem (see Methods). The average intensity within the left and right LC respectively were 0.81 (SD = 0.05) and 0.80 (SD = 0.06). The difference between them was not significant, paired t-test, t(20) = 1.91, p = 0.071.

3.3. Quality assessment of denoising procedures

To assess the effectiveness of the different denoising procedures we calculated tSNR and DVARS. Both measures were calculated for the whole brain as well as GM, HPC, V1, vmPFC, MC, AC, and LC (Fig. 3). As a first step, analyses focused on comparing the four regression-based pipelines to investigate the effects of including or excluding RETROICOR and 4V regression. The best regression-based pipeline was then pitted against the two ICA-based approaches. Analyses utilized repeated-measures analysis of variance (ANOVA; R Core Team, 2020) with participant as a random effect.

Fig. 3.

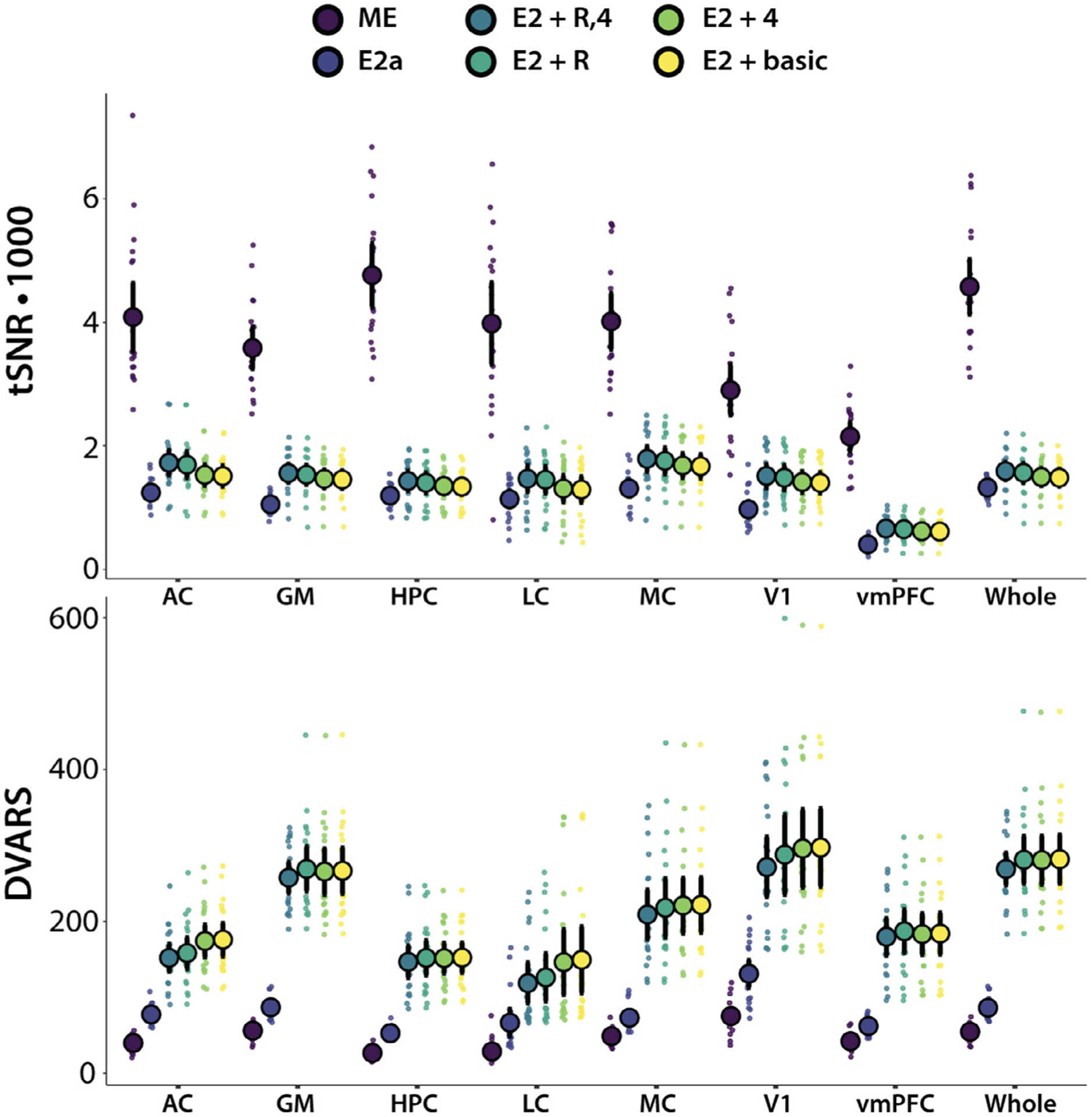
tSNR and DVARS across pipelines in select ROIs. AC = auditory cortex; GM = grey matter; HPC = hippocampus; LC = nmT1-traced locus coeruleus; MC = motor cortex; V1 = primary visual cortex; vmPFC = ventromedial prefrontal cortex; and whole brain

An ANOVA on tSNR following regression-based denoising of the E2 data included three fixed factors: ROI (7 ROI levels: GM, HPC, LC, MC, V1, vmPFC, AC), application of RETROICOR (included/excluded), and inclusion of 4V regression (included/excluded). tSNR varied across ROIs: it was greatest in MC and AC, and lowest in vmPFC, F(6,114) = 52.76, p < .001, η_p² = .735 (95% CI: .638–.779). Both RETROICOR and 4V regression significantly increased tSNR: main effect of RETROICOR, F(1,19) = 33.71, p < .001, η_p² = .634 (.311–.773), main effect of 4V regression, F(1,19) = 32.97, p = < .001, η_p² = .634 (.304–.769). The interaction between RETROICOR and 4V regression was not significant, F(1,19) = 3.509, p = .077, η_p² = .156 (0–.420). The effects of RETROICOR and 4V regression on tSNR varied across ROIs and were largest in the MC and AC, but smallest in the vmPFC, resulting in interactions between ROI and RETROICOR, F(6,114) = 5.806, p < .001, η_p² = .234 (.078–.325), and also ROI and 4V regression, F(6,114) = 4.59, p < .001, η_p² = .195 (.048–.283). Therefore, both denoising procedures removed significant sources of noise from the E2 data. Consequently, E2 + R,4 is the superior regression-based denoising approach.

The second tSNR analysis contrasted the ME denoising with two E2 pipelines: E2a, which included ICA-AROMA, and E2 + R,4. An ANOVA with denoising procedure and ROI as factors revealed a main effect of denoising, F(2,38) = 245.3, p < .001, η_p² = .933 (.878–.953), and of ROI, F(6,114) = 46.27, p < .001, η_p² = .709 (.603–.757). The effect of denoising procedure varied by ROI, F(12,228) = 22.31, p < .001, η_p² = .540 (.431–.587). Post-hoc, Holm-adjusted pairwise t-tests revealed significant differences between all pipelines, such that tSNR was highest for ME-ICA, second highest for E2 + R,4, and lowest for E2a (all p’s < .001). Relative to the best denoising procedure for E2 analyses, ME denoising increased tSNR by a factor of about 2.5, on average, with its largest benefits in regions susceptible to signal dropout due to field inhomogeneities, such as HPC.

We investigated the same effects on DVARS averaged over time. An ANOVA on DVARS following regression based denoising indicated that there were significant main effects of applying RETROICOR, F(1,19) = 6.868, p = .017, η_p² = .263 (.008–.515), and of using 4V regression, F(1,19) = 4.372, p = .050, η_p² = .187 (0–.449). DVARS also varied across ROIs, F(6,114) = 25.27, p < .001, η_p² = .571 (.429–.639): it was lowest in LC and HPC, and highest in V1. The effect of RETROICOR on DVARS varied by ROI, resulting in an interaction, F(6,114) = 4.473, p < .001, η_p² = .191 (.045–.278). However, all interactions involving 4V regression did not reach not significance, largest F(1,19) 2.413, p = .137, η_p² = .113 (0–.376).

A second analysis examined the effects of ICA-based denoising approaches by comparing E2 + R,4 against E2a and ME denoising in an ANOVA. This revealed a main effect of pipeline, F(2,38) = 304.4, p < .001, η_p² = .941 (.896–.957), as well as ROI, F(6,114) = 44.21, η_p² = .699 (.590–.749). The impact of pipeline varied by ROI, as evidenced by an interaction, F(12,228)–16.66, p < .001, η_p² = .467 (.348–.519). Post-hoc, Holm-adjusted pairwise t-tests showed that ME reduced DVARS most, followed by E2a, and then E2 + R,4 (all p’s < .001).

Because E2 + R,4 and E2a were the best performing pipelines for either tSNR or DVARS, all subsequent analyses considered both those E2 pipelines against the ME pipeline. Recall that for all the pipelines in this dataset, the underlying neural activity is the same because they come from the same scan. Analyses comparing a 1E-fMRI acquisition (with TR optimized for our scanner and given certain scan parameters) to an ME-fMRI acquisition acquired in separate scans are reported in the Supplemental Materials.

3.4. T2* relaxation estimates

ME-fMRI can be used to estimate T2* decay rates within each voxel to optimally combine the echoes for each voxel of the brain (Kundu et al., 2017). Variance in T2* decay rates across the brain and across individuals was examined by calculating the mean and the standard deviation of the individual T2* values generated by meica.py in native space (Fig. 4). As expected, these maps illustrate that T2* values vary across regions: values were relatively low in vmPFC (M = 19.899 ms, SD = 2.608), more moderate in medial occipital cortex (e.g., V1, M = 39.691 ms, SD = 4.317), and high in both auditory (M = 51.812 ms, SD = 2.756) and motor cortex (M = 52.208 ms, SD = 6.131). Echo times were moderate and similar for the LC (M = 47.385 ms, SD = 8.801) and K1 (M = 48.211 ms, SD = 6.697). Regions more susceptible to signal dropout due to field inhomogeneities, such as ventral temporal cortex, also showed greater variance across individuals. Therefore, at least part of the tSNR and DVARS advantage for ME-ICA denoising should reflect the optimal combination of echoes using the T2* values for each individual and voxel (Kundu et al., 2017).

Fig. 4.

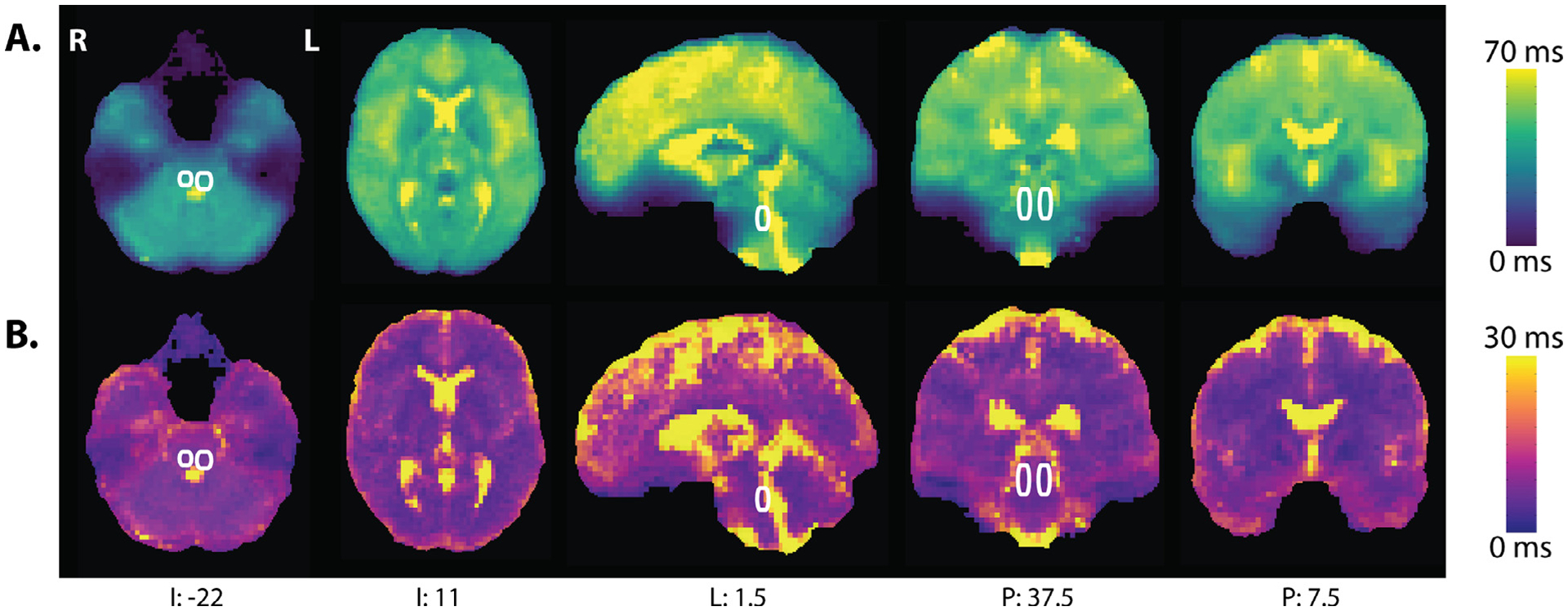
T2* map computed with t2smap.py as part of the meica.py pipeline. A) Mean observed T2* relaxation across participants. B) Standard deviation of observed T2* relaxation. The location of the LC, outlined in white, is based on the heat map of LC ROIs as illustrated in Figure 2. Data in MNIa, with coordinates in LPI. Descriptive statistics for various ROIs were calculated in native space.

3.5. Intrinsic Functional Connectivity Analysis

3.5.1. Specificity of Seeds

To examine whether estimates of LC function differ across ROI definitions, data acquisition approaches, and blurring we computed the correlation coefficients between time series of multiple brainstem regions (Table 1). Because the K1 and K2 time series ROIs were highly correlated (r = .850–.955), analyses focused on the more conservative K1 ROI.

Table 1.

Means and standard deviations (in parentheses) of correlations among the brainstem ROI time series for E2 + R,4, E2 with ICA-AROMA, and ME-ICA

		rK1, K2	rK1, PT	rK1,PT • LC	rK2, PT	rK2,PT • LC	rK1, LC	rK2, LC	rLC, PT
E2 + R,4	nb	.850 (.317)	.233 (.175)	.189 (.174)	.254 (.175)	.222 (.171)	.388 (.265)	.475 (.278)	.161 (.171)
	b5	.948 (.292)	.366 (.216)	.271 (.214)	.390 (.108)	.310 (.223)	.662 (.297)	.693 (.296)	.268 (.197)
E2a	b5	.947 (.261)	.379 (.205)	.239 (.175)	.403 (.213)	.282 (.181)	.684 (.312)	.703 (.280)	.315 (.205)
ME	nb	.934 (.302)	.430 (.191)	.278 (.225)	.446 (.172)	.311 (.245)	.658 (.274)	.666 (.332)	.353 (.283)
	b5	.955 (.303)	.459 (.203)	.302 (.236)	.473 (.179)	.330 (.260)	.717 (.282)	.717 (.333)	.372 (.284)

Note: Pearson’s r values were Fisher transformed to compute the mean and standard deviation and then transformed back. Values are presented for blurred and native blur data for the E2 + R,4 pipeline and ME pipeline. The E2 ICA-AROMA pipeline (E2a) was only performed with 5 mm FWHM blur.

Correlations for PT with LC and K1 ROIs were used to evaluate whether each ROI captured patterns of activity that were present in other parts of the brainstem. Because it did not include a native blur condition, the E2a pipeline was not directly compared to E2 + R,4 and ME seeds. Values for the blurred E2a data are included in Table 1 for reference, however.

Correlations with PT were greater for K1 than LC ROIs, ME than E2 + R,4 data, and when the data were blurred to 5 mm FWHM. However, the effects of blurring were greater for E2 + R,4 than for the ME data and for K1 than for LC. These differences were significant in an ANOVA on the Fisher-transformed correlations with PT: correlations with the PT time series significantly differed across K1 and LC ROIs, F(1,19) = 6.452, p = .02, η_p² = .253 (95% CI: .004–.505), denoising pipeline, F(1,19) = 8.271, p = .010, η_p² = .303 (.021–.544), and blur, F(1,19) = 42.89, p < .001, η_p² = .693 (.389–.807). Blurring increased the correlation with PT more for LC than it did for K1, as evidenced by an interaction between blur and ROI, F(1,19) = 6.509, p = .020, η_p² = .255 (.005–.506). It also increased correlations more under E2 + R,4 than ME, interaction between blur and pipeline, F(1,19) = 47.69, p < .001, η_p² = .715 (.424–.820). Not surprisingly, methods that reduced noise in the data (ME-ICA denoising and blurring) increased the correlations among regions. The benefits of blurring were smaller for ME, relative to E2 + R,4, perhaps reflecting the improved tSNR and DVARS.

The moderate correlations between PT and K1 or K2 combined with the weaker correlations between LC and the PT, suggest that the LC ROI was less likely to capture activity from the surrounding pons than were K1 and K2. To confirm this, we regressed out the LC signal from the K1, K2, and PT ROIs and correlated their residuals to produce partial correlations between K1 and PT as well as K2 and PT. These partial correlations remained relatively high, indicating that the atlas-based signal that correlates with the PT reflects substantial activity outside the individually defined LC ROIs.

3.5.2. Correlations among functional connectivity maps

Differences in the iFC maps generated by each method should lead to weaker correlations among maps, particularly if those maps have already been thresholded. Therefore, the effects of seed ROI, denoising approach, and blur on estimates of functional connectivity between the LC and the rest of the brain were characterized by determining the correlation and mutual information (Hausser, Strimmer, & Strimmer, 2012) of the resulting maps. For these analyses, only those voxels that were in the top 15% of either map and that were not in the K1 and LC ROIs were considered because differences in high correlation voxels other than in those ROIs would be of more interest to researchers. Because voxels that survived thresholding in either iFC map were used, correlations will decrease as differences in voxel values increase and as the number of voxels that survive thresholding in one map do not survive thresholding in the other (overlap in thresholded maps is analyzed in the next section).

Voxel-to-voxel correlations across maps generated with E2 pipelines and ME data were small and often negative, and mutual information was low (Table 2; see also Fig. 5). Keeping pipeline and blurring constant and only differing in use of LC or K1, the correlations remain moderate, with mutual information in the same low range as for comparisons between E2 and ME (Table 3; Fig. 5). Thresholded functional connectivity maps generated from E2 rather than ME data, or from K1 rather than LC ROIs, therefore contained different information, despite all coming from the same scan and aiming to characterize connectivity with (putative) locus coeruleus. The differences between the E2 and ME maps could have resulted from the presence of spurious correlations in the data (Yarkoni, 2009), which may survive thresholding of one map but not the other. Spurious correlations are less likely for the ME data than the E2 data, as higher tSNR should reduce their likelihood (Yarkoni, 2009).

Table 2.

Relationships between thresholded maps that differed in preprocessing

Map X	Map Y	Pearson’s rxy	Mutual Information
E2 + R,4 K1 nb	ME K1 nb	−.164	0.107
E2 + R,4 K1 b5	ME K1 b5	.080	0.096
E2 + R,4 LC nb	ME LC nb	−.288	0.085
E2 + R,4 LC b5	ME LC b5	−.222	0.114
E2a K1 b5	ME K1 b5	.057	0.102
E2a LC b5	ME LC b5	−.128	0.040
E2a K1 b5	E2 + R,4 K1 b5	.430	0.212
E2a LC b5	E2 + R,4 LC b5	.139	0.117

Fig. 5.

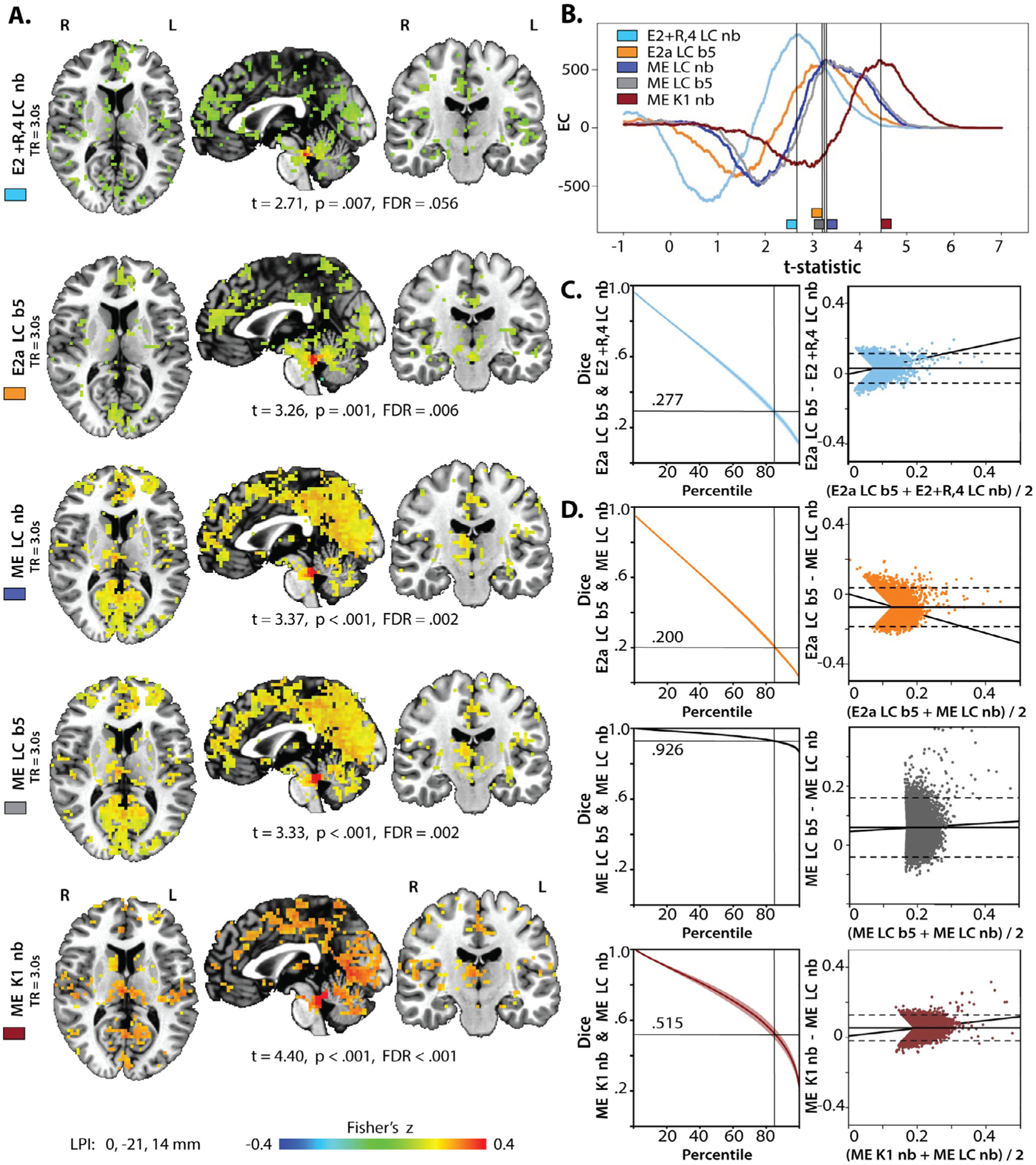
Intrinsic functional connectivity maps generated with five preprocessing pipelines. A) iFC maps for the different LC seeds with various ME and E2 pipelines. Maps were thresholded at the t-statistic with the maximum EC. B) EC for all iFC maps as a function of the t-statistic. C) Dice coefficients across percentiles and Bland-Altman plots comparing the E2 + R,4 pipeline to the E2a pipeline. Horizontal line indicates the 85th percentile. This served as the threshold for analyses reported in Tables 2–4 and for the Bland-Altman plots in the right column. Solid line: mean difference, dashed lines: +/−1.96 of the standard deviation of the differences. D) Dice coefficients and Bland-Altman plots to compare the ME LC nb iFC map against other preprocessing approaches. Note the smaller range on the ordinate axis for the comparison against ME LC b5.

Table 3.

Relationships between thresholded maps that differed in seed ROI

Map X	Map Y	Pearson’s rxy	Mutual Information
ME LC nb	ME K1 nb	.347	0.100
ME LC b5	ME K1 b5	.439	0.139
E2 + R,4 LC nb	E2 + R,4 K1 nb	.117	0.097
E2 + R,4 LC b5	E2 + R,4 K1 b5	.607	0.164
E2a LC b5	E2a K1 b5	.548	0.113

A small amount of blurring before extracting the seed had little effect on the resulting functional connectivity maps, as indicated by the strong correlations and higher mutual information (Table 4; Fig. 4). The effects of blurring were greater for E2 data and when the LC seed was used. Thus, blurring may not produce large differences in functional connectivity maps generated from the K1 ROI, but may impact maps generated from the smaller LC ROIs and with single-echo data.

Table 4.

Relationships between thresholded maps that differed in blur

Map X	Map Y	Pearson’s rxy	Mutual Information
ME K1 nb	ME K1 b5	.990	0.736
E2 + R,4 K1 nb	E2 + R,4 K1 b5	.904	0.339
ME LC nb	ME LC b5	.976	0.625
E2 + R,4 LC nb	E2 + R,4 LC b5	.783	0.213

3.5.3. Characterizing the effects of seed ROI, data type, and blur on functional connectivity maps

To better characterize the extent to which different methods and pre-processing steps result in different LC connectivity maps, we visualized and quantified differences in map topography and correlation values for four central comparisons (Fig. 5): (i) ME LC vs E2a LC to evaluate the effects of data type, (ii) ME LC vs ME K1 to evaluate the effects of ROI type, and (iii) ME LC nb vs ME LC b5 to evaluate the effects of blurring. We also compared (iv) E2a LC b5 to E2 + R,4V b5 to examine maps generated by regression-based versus ICA-based denoising approaches to single-echo data.

To quantitatively compare the topography of the functional correlation maps, the Euler characteristic (EC) was calculated with SPM12 (rev. 7487; Penny et al., 2011) for maps thresholded across a range of t-statistics (Fig. 5 B). Negative ECs occur when voxels that survive the threshold form largely connected topographies with holes rather than disconnected clusters. EC increases and becomes positive as voxels that survive the threshold form disconnected clusters (Bowring et al., 2019; Brett, Penny, & Kiebel, 2003; Worsley, Marrett, Neelin, Vandal, Friston, & Evans, 1996). Therefore, each map was thresholded to the t-statistic that corresponded to the maximum EC to maximize the number of disconnected clusters in a map. ECs were highest for the E2 + R,4 LC nb map (805). They were lower and similar for the E2a LC b5, ME K1 nb, ME LC nb, and ME LC b5 (589, 581, 578, and 573 respectively). However, the maximum ECs occurred at lowest t-statistics for the two E2 maps and at the highest t-statistic for the ME K1 nb map. The EC for ME K1 nb was negative around the peak ECs used for three other maps (E2a LC nb, ME LC nb, and ME LC b5), capturing widespread, nonspecific activation (particularly along the midline).

Agreement in which voxels survive increasingly conservative thresholds was evaluated by calculating the Dice coefficient across thresholded maps. Percentile thresholds were used to equate the number of surviving voxels in each map. Consistent with the correlation analyses, Dice coefficients decreased rapidly when the E2a LC maps and ME LC nb map were compared (Fig. 5C–D). Decreases in the Dice coefficient for the ME LC nb and ME K1 nb comparison were less steep, but still indicated only modest overlap at high thresholds. Dice coefficients for the ME LC nb and ME LC b5 maps remained above .9 at high thresholds.

To investigate whether differences in the maps are systematic or reflect random variation across methods, Bland-Altman plots (Bland & Altman, 1999; Bowring et al., 2019) were created. These visualize differences in the estimated correlation coefficient in the two maps as a function of their mean values. Visual inspection of these plots indicates that values in the E2a LC b5 map were higher than the E2 + R,4 LC nb map (Fig. 5C), suggesting that ICA-AROMA can boost statistical power of single echo data analyses. However, ME-fMRI remains advantageous as ME LC nb had systematically higher values than did E2a LC b5 (Fig. 5D), despite no additional blurring. Small differences between the ME LC b5 and ME LC nb maps further suggest that blurring did not result in large shifts in the mean estimated correlations. In contrast, utilizing the K1 ROI rather than the LC ROI did produce large differences in the maps: the mean of the difference in estimated correlations was nearly 1.96 standard deviations above 0, with larger differences at more extreme mean values.

3.5.4. Characterization of LC functional connectivity

To further characterize differences in the iFC maps, we investigated the proximity of the peaks in the ME LC nb map to peaks in each of the three other maps. Twenty-five peaks were extracted from each map using AFNI’s 3dmaxima with a minimal distance of 18 mm (6 voxels) between a given ranked peak and the next. This approach first finds the top peak in the map and then excludes any other peaks within 18 mm before searching for the next highest peak. Table 5 lists the top 25 peaks for the ME LC nb map as well as the rank of the nearest peak in several comparison maps (also see additional tables in Supplemental Materials for top peaks in other maps). Some caution is warranted in interpreting these data, since peaks that do not make it into the top 25 of one map may nevertheless fall close to a peak that did make it into the top peaks of another map.

Table 5.

Ranked peaks in ME LC nb and their proximity to peaks in the other iFC maps

Rank	Area	Coordinates	Fisher’s Z (%-tile)	Rank of nearest peak in E2a LC b5 (mm distance)	Rank of nearest peak in ME LC b5 (mm distance)	Rank of nearest peak in ME K1 nb (mm distance)
1	R. Locus coeruleus	4–41–19	0.562 (99.99)	1 (3)*	1 (11.2)*	1 (9)*
2	R. Thalamus	4–23 14	0.301 (99.95)	18 (13.4)*	2 (0)*	3 (0)*
3	L. Precuneus	−2–41 53	0.294 (99.95)	22 (13.4)*	3 (0)*	20 (15)*
4	R. Visual cortex / BA 18	19–77–7	0.287 (99.94)	24 (9.9)*	4 (0)*	4 (0)*
5	R. Anterior Cingulate	10 34 20	0.285 (99.94)	3 (8.5)*	5 (0)*	25 (3)*
6	R. Hippocampus / Parahipp. gyrus	16–38–1	0.282 (99.93)	17 (12.4)*	6 (9)*	7 (6.7)*
7	L. Anterior Cingulate	−11 37 14	0.275 (99.93)	7 (17.2)*	11 (0)*	25 (19.2)
8	L. Precuneus	−2–65 20	0.275 (99.90)	11 (19.4)	8 (0)*	2 (16.4)*
9	L. Retrosplenial Cortex / BA 30	−5–50 8	0.274 (99.89)	10 (11.2)*	7 (0)*	21 (0)*
10	L. Hippocampus / Parahipp. gyrus	−29–41–10	0.273 (99.89)	2 (12.7)*	16 (13.4)*	18 (9)*
11	R. Precuneus	16–65 26	0.272 (99.89)	11 (7.3)*	10 (7.3)*	2 (26.5)
12	L. Angular gyrus	−44–59 41	0.271 (99.88)	4 (29.1)	15 (0)*	5 (42.5)
13	L. Visual cortex / BA 17–18	−26–89–10	0.235 (99.85)	12 (13.1)*	12 (0)*	12 (6)*
14	L. Precuneus	−2 −74 62	0.267 (99.84)	22 (21.2)	19 (9)*	11 (21.2)
15	L. Hippocampus / Parahipp. gyrus	−11–32–1	0.266 (99.84)	2 (14.7)*	13 (0)*	18 (15.6)*
16	L. Visual cortex / BA 19	−44–77–1	0.265 (99.84)	12 (23.6)	20 (0)*	14 (7.3)*
17	R. Visual cortex / BA 17–18	1–83–4	0.265 (99.83)	9 (9)*	17 (0)*	2 (15)*
18	R. Parieto-occip. fissure	10–83 47	0.265 (99.83)	11 (21.4)	9 (0)*	11 (0)*
19	L. Precuneus	−2–59 47	0.263 (99.81)	22 (13.4)*	3 (19.0)	20 (20.1)
20	L. Posterior Cingulate	−23–62 11	0.262 (99.80)	4 (23.6)	21 (3)*	21 (21.8)
21	L. Precuneus	−5–53 68	0.261 (99.79)	22 (9.5)*	19 (15)*	20 (5.2)*
22	R. Dorsomedial Prefrontal Cortex / BA 9	28 43 20	0.260 (99.78)	3 (26.3)	18 (0)*	25 (22.8)
23	R. Transverse gyrus / BA 42	46–29 11	0.258 (99.75)	21 (17.5)*	14 (0)*	16 (10.8)*
24	L. Medial Superior Frontal gyrus	−2 25 41	0.257 (99.73)	20 (15)*	23 (0)*	25 (24.6)
25	Subcallosal (parolfactory) area / BA 25	1 10–1	0.256 (99.72)	18 (27.3)	25 (0)*	8 (25.8)

Note: Coordinates are in LPI.

^{* =}peaks that were less than 18 mm apart and would be considered part of the same cluster by our peak finding algorithm. Labels for the area are based on the peak coordinates, center of mass for the peak’s cluster, and anatomical plausibility.

Consistent with the previous analyses, the percentage of peaks in the ME LC nb map that fell within 18 mm of a peak on another map was highest for the ME LC b5 map (24 of 25 peaks, or 96%), second highest for the E2a LC b5 map (17 peaks, 68%), third for ME K1 nb map (16 peaks, 68%), and lowest for E2 + R,4 LC nb (13 peaks, 52%).

4. General Discussion

A growing body of research on the functional and anatomical properties of the LC suggests that it plays a central role in a variety of cognitive processes and in neurodegenerative disease (Mather & Harley, 2016). However, characterizing LC function and anatomy in human fMRI has multiple challenges that have not been systematically investigated in the literature (Liu et al., 2017). This study addressed several of these challenges by comparing LC localization approaches, BOLD data acquisition and denoising approaches, and the use of conservative blurring on estimates of LC activity and functional connectivity. The analyses suggest that, while modest blurring may have limited effect on estimates of LC function, alternatives in LC localization method, data acquisition, and denoising approaches are likely to lead to different interpretations of the same data. These results are especially important and timely given the broader conversation in fMRI literature on the effects of pipeline variability (Botvinik-Nezer et al., 2020).

4.1. Localization of LC with a probabilistic atlas or nmT1 imaging

One purpose of this study was to investigate whether individually defining LC ROIs using nmT1 imaging produces substantially different results from using a probabilistic atlas. Probabilistic ROIs may not adequately account for variability in individual brainstem anatomy and LC shape and location (German et al., 1988; Keren et al., 2015). In addition, studies report a wide range of bilateral LC coordinates that sometimes go beyond the dimensions of the Keren atlas (Liu et al., 2017). The use of an ROI defined by coordinates or a group atlas, like the K1 ROIs used here, could therefore partially miss the LC, if not entirely, and capture activity from neighboring brainstem areas (e.g., the pontine tegmentum, medial cerebral peduncle, cranial nerve nuclei, and inferior colliculus; Neary, 2008). These neighboring areas play critical roles in processing motor and sensory information, which would confound analyses. Thus, despite the practical advantages of probabilistic atlases, the best way to isolate activity from the LC could still be to individually define ROIs using nmT1 imaging.

The results support this recommendation: the K1 ROIs were larger and tended to extend further rostrally and caudally than the individual LC ROIs, and there was only low to moderate overlap between the individually defined LC ROIs and K1 ROIs. Activity in the K1 ROIs was also more strongly correlated with activity and in the pontine tegmentum than was activity in the LC ROIs. These differences had consequences for estimates of LC connectivity: overlap between thresholded iFC maps generated by LC and K1 ROIs was moderate (.515 for the top 15% of voxels). The Keren atlas also produced stronger correlations overall, which caused less specific activity at thresholds used for the other maps, and the need for higher thresholds to isolate network clusters. In addition, although the LC and K1 ROIs produced maps with peaks that were near each other (i.e., thalamus, HPC, midline regions, and auditory and visual areas), the K1 iFC maps also included highly ranked peaks in primary and supplementary motor areas. Thus, the final iFC maps produced by K1 showed more widespread associations that also differed in their spatial topography from those produced by the nmT1-based LC ROIs.

4.2. Use of ME-fMRI versus 1E-fMRI

Because ME-ICA denoising may be particularly effective at reducing noise from motion and improving BOLD contrast (Power et al., 2018), another goal of this study was to characterize whether the resting state iFC maps differed between ME-fMRI and 1E-fMRI. Results suggested that ME and E2 data from the same run, thus reflecting the same brain activity, can result in different iFC maps. Overlap between ME and E2a iFC maps decreased rapidly as thresholds increased, correlations between the thresholded group level iFC maps were low, and only 68% of peaks in the ME LC nb map fell within 18 mm of the top peaks on the E2a LC b5 map. Though our results suggest that ICA-AROMA should be used with single echo data, they nevertheless demonstrate that the maps that resulted from the ICA-AROMA and ME-ICA pipelines differed both quantitatively (Fig. 5) and qualitatively (Tables 5; see also Supplemental Materials). These differences could reflect the ability to accommodate different optimal echo times across the brain and to remove components of the signal with non-BOLD-like characteristics when using ME-fMRI (Kundu et al., 2012). Indeed, ME-fMRI with ME-ICA was superior to 1E-fMRI in both tSNR and DVARS in every region examined, including the LC ROIs. Importantly, these differences are unlikely to be mitigated by using shorter TRs that are possible in a 1E-fMRI scan. Nearly identical patterns were observed when comparing ME-fMRI data to 1E-fMRI data acquired in a separate resting state scan and with a shorter TR (1.9 s; see Supplemental Materials). Thus, the use of ME-fMRI is advantageous, particularly with small regions like the LC.

ME-ICA is a relatively effective way to remove some sources of noise from fMRI data. It would be valuable for future research to systematically investigate how these gains in tSNR influence iFC patterns. Furthermore, it may be necessary to employ additional denoising methods to remove respiratory and cardiac noise in the BOLD signal itself (Power et al., 2018). Our ME-fMRI pipeline therefore included both WM and 4V regression (Dagli, Ingeholm, & Haxby, 1999; Windischberger et al., 2002). However, analyses that did not include the WM nuisance regressor resulted in similar outcomes, with correlations that were somewhat larger (Supplemental Materials).

4.3. Effects of blurring on the data

Because of the LCs size and proximity to the fourth ventricle, this study also addressed the effects of blurring prior to extracting the seed from the ROIs. The results suggest that this had only a small effect on the resulting iFC maps: correlations among the maps were strong, ECs for the two maps were similar, Dice coefficients were high, and Bland-Altman plots suggested small differences in the absolute magnitude of voxel correlations. This resulted in 96% of the peaks in the nb map falling within 18 mm of a cluster in the map with the blurred seed. Peaks that were further away were also in relatively similar brain regions. This suggests that blurring by a small amount before the LC seed is extracted may not have an appreciable effect on the conclusions of a study. These results do not undermine the importance of precisely localizing the LC, as both the nb and b5 maps were generated by ROIs that were centered on the manually defined ROIs. As the K1 ROI analyses demonstrate, imprecise localization could lead to differential outcomes in the data. In addition, blurring by larger amounts could increase the similarity between the LC and surrounding pontine areas (see also Supplemental Materials for iFC maps with more blurring).

4.4. Measuring neuromelanin content with nmT1 imaging

Although not the focus of the current study, many studies of the LC are concerned with individual differences in neuromelanin content. Liu et al. (2017) identified substantial methodological differences in how neuromelanin content is estimated using nmT1 images. Studies that use nmT1 signal intensity to estimate LC neuromelanin content have not always normalized signal intensity and those studies that did often used different reference regions. Among the studies that normalized signal intensity, the most common reference region was the PT, a large region with vague boundaries. Because the PT displays age-related signal decline, including in non-clinical populations (Clewett et al., 2016), it may not be an optimal choice for a reference. Studies also differ in the algorithms used to normalize signal intensity, differing in their use of peak or average LC signal. One consequence of these methodological differences may be greater variability in estimates of LC volume, which vary widely in reported studies and are different than what one would expect from post-mortem specimens (Liu et al., 2017). Despite these problems, nmT1 imaging remains the best avenue to measure in vivo individual differences in signal intensity. To mitigate some of these issues in our preprocessing of the nmT1 images, we applied a novel normalization approach that does not rely on only one of the specific regions commonly used in the LC literature, but instead relies on variance in the entire brainstem. This should reduce the influence of age-related changes in intensity to specific brainstem nuclei, although it remains possible that the brainstem as a whole shows age-related changes in average contrast. This possibility warrants future investigation with a sample of a wider age range.

4.5. Functional connectivity of the LC in typical young adults

Previous functional studies on the LC have exclusively been performed using 1E-fMRI and frequently used the Keren 2 SD atlas. Across those studies, regions that typically emerge in iFC analyses are the prefrontal cortex, cerebellum, right supplementary motor area, cingulate cortex, thalamus, visual cortex, lingual and fusiform gyrus, insula, amygdala, and the hippocampus (e.g., Bär et al., 2016; Köhler, Wagner, & Bär, 2019); Kline et al., 2016; Murphy et al., 2014; Sterpenich et al., 2006). Nearly all these regions were ranked highly in our ME K1 nb map. The amygdala did not rank in the top of any of our maps, possibly because it was too close to peaks in the hippocampus to survive our peak selection procedure.

Other studies on LC iFC have not always identified the same regions. For example, Song et al. (2017) showed connectivity to the reticular formation, ventral tegmental area, and caudate. None of our pipelines ranked peaks in the reticular formation highly (other than peaks in the LC), although these (or nearby) regions may have survived our Euler characteristic-based thresholding procedure. The ventral tegmental area was ranked 6th in the E2a LC b5 and ME K1 nb map, however. Zhang, Hu, Chao, & Li (2016) found positive connectivity to inferior temporal cortex, anterior parahippocampal gyrus, posterior insula, ventrolateral thalamus, and a large region in the cerebellum. Intriguingly, they found negative connectivity to several regions that were positively correlated with the LC in our maps (similar to others), including the bilateral visual cortex, middle and superior temporal cortex, precuneus, retrosplenial cortex, posterior parahippocampal cortex, frontopolar cortex, caudate, and dorsal and medial thalamus. An important methodological difference between our study and theirs, however, was the use of whole brain (global) signal regression, which can introduce negative correlations (Fox, Zhang, Snyder, & Raichle, 2009). We will return to this point below.

One intriguing peak found in our maps was a cluster in the basal forebrain (subcallosal area in Table 5). This cluster has not been widely reported in studies of LC iFC, perhaps because it is located in a part of the brain that is susceptible to field inhomogeneities and difficult to measure using 1E-fMRI. Previous work has demonstrated that ME-fMRI can effectively recover signal from this region during pre-processing (Markello et al., 2018). Relative to our 1E-fMRI maps, the clearer presence of this region in our ME maps is particularly important: studies on the basal forebrain’s physiology and function suggest an important anatomical and functional relationship between these regions and the LC in the regulation of attention and memory (e.g., Mesulam, 2013; Ljubojevic, Luu, & De Rosa, 2014; Sarter, Hasselmo, Bruno, & Givens, 2005; Yu & Dayan, 2005)

4.6. Pupillometry as a means of investigating LC function

Pupillometry is increasingly used as an indirect, non-invasive measure of LC activity (e.g., Einhäuser, Stout, Koch, & Carter, 2008; Eldar, Niv, & Cohen 2016; Gilzenrat, Nieuwenhuis, Jepma, & Cohen, 2010; Jepma and Nieuwenhuis, 2010; Murphy et al., 2014). Recent neuroimaging and electrophysiological work has shown a strong, positive relationship between activity in the LC and increases in pupil size (Breton-Provencher & Sur, 2019; Joshi, Li, Kalwani, & Gold, 2016; Murphy et al., 2014). However, they also demonstrate that pupil diameter is associated with activity in other brainstem areas, including those that are near the LC (e.g., inferior colliculus, superior colliculus, nucleus incertus; e.g., Costa & Rudebeck, 2016; Joshi et al., 2016; Szőnyi et al., 2019). Efforts to use pupillometry to verify that certain voxels are within the LC have found activations throughout the brainstem, particularly in dorsal areas (near the colliculi) and in oddball tasks (Murphy et al., 2014). This, combined with our data, indicates that caution is warranted when using pupillometry to isolate LC activity: larger ROIs from probabilistic atlases (like the K1 ROI) produce appreciably different iFC maps than individual LC ROIs.

The need for caution is corroborated by the pupillometry data acquired in a second dataset (Supplemental Materials). Consistent with the results reported in this paper, denoising procedure influenced iFC maps generated using a seed reflecting pupil size. Pupil based iFC maps also differed from those generated from the LC seed, and overlapped little when thresholded at the 85^th percentile. A systematic investigation of these issues is outside the scope of the current paper, but it is evident that a similar systematic investigation is warranted into the effects of pupillometry procedures and preprocessing approaches on the extent to which pupil size can offer noninvasive investigation of LC activity.

4.7. Limitations and further considerations

There are several limitations to the results presented here. First, we did not explore several other denoising approaches for 1E or ME data (e.g., ANATICOR) and it is possible that these would have led to different outcomes (e.g., Dipasquale et al., 2017; Jo et al., 2010; for a review of several common denoising procedures, see Caballero-Gaudes & Reynolds, 2017). Second, a common denoising strategy in resting state iFC analyses is to regress out the mean signal across the brain (global signal) to reduce the contributions of physiological and motion related artifacts (Liu, Nalci, & Falahpour, 2017). Although some argue that global signal regression is the most effective way to remove physiological noise (e.g. Power et al., 2018), it does contain functional signals (e.g., Schölvinck, Maier, Frank, Duyn, & Leopold, 2010), including those related to vigilance (e.g., Liu et al., 2017). This is of particular concern for studies of the LC because it is involved in regulating vigilance both on and off-task (e.g., Aston-Jones et al., 1994; Aston-Jones et al., 2007), and has widespread projections throughout the brain (e.g., Schwarz & Luo, 2015). To avoid removing LC related activity, we therefore utilized WM nuisance regression and bandpass filtering (with a commonly applied range) to reduce the contributions of respiration, heart rate, and movement to the EPI data (Power et al., 2018). While this approach also could remove meaningful LC-related signal as well as noise, it was less aggressive than global signal regression. In analyses that utilized global signal regression (Supplemental Materials), correlations were weaker, included negative values (a common consequence of global signal regression; Fox et al., 2009; Zhang et al., 2016), and included only pontine areas centered on the respective seed when thresholded at p = .05. New approaches, such as temporal ICA (Glasser et al., 2018), may offer other ways to address physiological noise captured by the global signal and their application will require future investigation.

There are also pragmatic concerns associated with ME-fMRI, which requires longer TRs than 1E-fMRI and greater computational resources. Shorter TRs are sometimes needed to characterize the hemodynamic response or when tasks include events that are closely spaced. Under these conditions, multi-echo multi-band techniques (MEMB; e.g., Olafsson, Kundu, Wong, Bandettini, & Liu, 2015) could be used. One systematic evaluation of ME-ICA with MEMB suggests that this approach may offer additional benefits by improving estimates of the hemodynamic response (Kundu et al., 2017). Although multi-band techniques were outside the scope of the current study, they certainly warrant separate investigation in combination with ME-fMRI. However, ME-fMRI also has higher computational costs than 1E-fMRI that would be exacerbated by combining it with multi-band imaging. Because acquiring three echoes triples the amount of data acquired during a scan, ME-fMRI requires more storage than 1E-fMRI. In addition, running ME-ICA adds substantial processing time to preprocessing. Depending on a given study’s experimental goals, timeframe, and budget, these factors may reduce the utility of ME-fMRI with ME-ICA, despite the clear and well-established boost to data quality and power. Nevertheless, our second dataset with shorter TRs and an optimized single-echo run (ME-fMRI, TR = 2.5 s; 1E-fMRI, TR = 1.9 s) reproduced and corroborated the main findings in the analyses presented in this paper.

The ability to use nmT1 imaging may also be limited to particular scanners and populations. Neuromelanin levels change over the lifespan (Halliday, Fedorow, Rickert, Gerlach, Riederer, & Double, 2006) and differ between clinical and non-clinical populations (Braak, Thal, Ghebremedhin, & Del Tredici, 2011; Marien, Colpaert, & Rosenquist, 2004). Researchers interested in the effects of neuromelanin on cognitive decline in the elderly, cognitive development in childhood, or the mediating role of neuromelanin on cognitive differences between clinical and non-clinical populations, may therefore have to consider alternative ways of localizing the LC. Furthermore, nmT1 scanning may work best with 3T scanners, as it has a better signal to noise ratio than 1.5T (Uğurbil et al., 1993) but none of the unique challenges that come with human imaging at 7T or higher (Ladd et al., 2018). However, the exact benefits and disadvantages that come with scanning pontine nuclei at different field strengths remain unexplored.

It will be important for future research to more extensively evaluate the contributions of different volume registration approaches for characterizing LC function. The small size of the LC (within-plane diameter of the LC is about 2.5 mm; Fernandes et al., 2012) and coarse spatial resolution of functional images (usually 2 or 3 mm isotropic voxels) also make it critically important to align the EPI data and the ROIs as accurately as possible. However, many registration algorithms are optimized for aligning the neocortex rather than the brainstem to an atlas. The brainstem may be best aligned to group data if it is separated from the rest of the brain and nonlinearly warped to the template (Tona et al., 2017). However, such algorithms are not widely used.

Finally, in-house algorithms that partially or fully automate LC segmentation are still in development, with no systematic comparison existing yet between manual and automated methods (e.g., Betts et al., 2019; Chen et al., 2014; Morris et al., 2020). As these algorithms become more widely adopted, it will be important for future research to compare their resultant LC characterization to those presented here.

5. Conclusion

fMRI studies of LC function and structure have been hampered by the difficulties involved in localizing the LC, isolating LC activity from other nearby regions, and removing the effects of noise from motion and physiology on BOLD data (Liu et al., 2017). By systematically investigating the benefits of using nmT1 images, ME-fMRI, and conservative amounts of blurring, this study has found that the methods used to localize the LC, acquire BOLD data, and denoise it may have significant effects on how LC function is characterized. Although using nmT1 images to localize the LC necessitates additional scan time and manual tracing, these efforts may lead to greater specificity in the iFC maps. In addition, ME-fMRI with ME-ICA denoising protocols increased the quality of the data and revealed a cluster in the basal forebrain, a region that is otherwise susceptible to signal drop out (Park et al., 1988). Although there is no ground truth for what the functional characterization of the LC must look like across various measures, our results do suggest that, when possible, the use of ME-fMRI data acquisition combined with nmT1-based localization should increase confidence in one’s characterization of LC connectivity. Whatever methods are chosen, however, future LC researchers must carefully consider these potential tradeoffs in their methodology and nuance findings accordingly.

Abbreviations:

LC

locus coeruleus

4V

4th ventricle

NE

norepinephrine

nmT1

neuromelanin-weighted T1

iFC

intrinsic functional connectivity

1E-fMRI

single-echo fMRI

ME-fMRI

multi-echo fMRI

K1, K2

binary atlas from Keren, Lozar, Harris, Morgan, & Eckert (2009), 1SD and 2SD 1E, datasets with optimized single echo (TR = 1.9 s)

ME

multi-echo dataset

E2

second echo of the multi-echo dataset

1E+basic

basic denoising pipeline, including WM and motion regression (6 parameters and first derivatives, 12 total) on the 1E-fMRI data

1E+4

basic denoising, with the addition of 4V denoising

1E+R

basic denoising, with the addition of RETROICOR

1E + R,4

basic denoising, with the addition of both 4V and RETROICOR denoising

1Ea, 1E+R,4

with the addition of ICA-AROMA in lieu of basic motion regression

E2+basic

basic denoising pipeline, including WM and motion regression (6 parameters and first derivatives, 12 total) on the second echo data (l-E2, s-E2)

E2+4

basic denoising, with the addition of 4V denoising

E2+R

basic denoising, with the addition of RETROICOR

E2+R,4

basic denoising, with the addition of both 4V and RETROICOR denoising

E2a, E2+R,4

with the addition of ICA-AROMA in lieu of basic motion regression

ME, ME-ICA pipeline

with RETROICOR, WM, 4V, and 6 motion parameters (no derivatives) on the multi-echo data (l-ME, s-ME)

nb

native blur (at least 3 mm with 3 mm isotropic voxels)

b5

blurring brought up to 5 mm FWHM (AFNI’s 3dBlurToFWHM)

LPI

Left-Posterior-Inferior reference frame

MNI152

T1 MNI-152 0.5 mm iso-voxel standard atlas

MNIa

MNIa_caez_N27 standard atlas

Data and Code Availability Statement

Data from the studies reported in the main manuscript and the supplemental materials can be made available upon reasonable request and with proper approval from relevant research and ethics entities. Most analyses used publicly available software (AFNI, FSL, meica.py). Annotated analysis scripts for AFNI, FSL, MATLAB, Python, and R can be found on the GitHub of author HBT (https://github.com/HamidTurker).