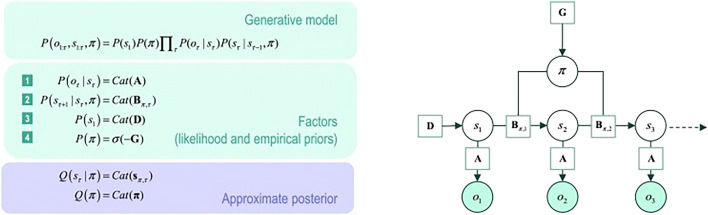
Fig. 1.

Example of a generative model in AI (Active Inference). A generative model is a probabilistic specification of how outcomes are caused. Usually, the model is expressed in terms of a likelihood (the probability of consequences given causes) and priors over causes. Examples of these probability distributions are provided in the green boxes. Bayesian model inversion refers to the inverse mapping from consequences to causes; i.e. estimating the hidden states that cause outcomes. In approximate Bayesian inference, one specifies the form of an approximate posterior distribution (blue box) with a specified functional form—that is chosen to make model inversion tractable. Left panel: these equations (in the green boxes) specify the generative model: the likelihood is specified by a matrix A. The elements of A encode the probability of each outcome for each hidden state. Cat means a categorical probability distribution. The priors include probabilistic transitions (in B matrices) among hidden states that can depend upon actions, which are determined by policies (i.e., sequences of actions denoted by π). The key aspect of this generative model is that policies are more probable a priori if they minimize the expected free energy G, which depends upon prior preferences about outcomes or costs (encoded by C). Finally, the vector D specifies prior beliefs about the initial state. This completes the specification of the model in terms of parameters that constitute A, B, C, and D. Right panel: the accompanying generative model shown as a Bayesian dependency graph: this Bayesian graph depicts the conditional dependencies among hidden states and how they cause outcomes. Open circles are random variables (hidden states and policies), while filled circles denote observable outcomes. Squares indicate fixed or known variables, such as the model parameters (See Friston, Parr, De Vries (2017) for a detailed explanation of the variables and mathematics).