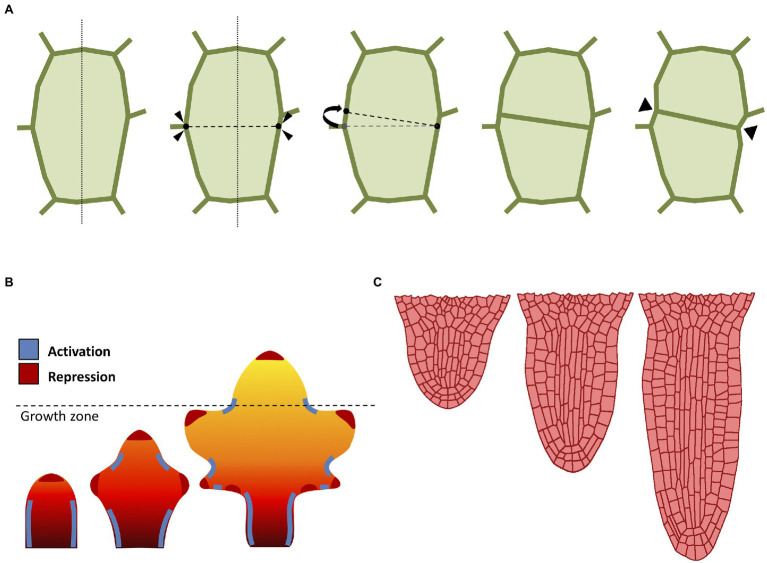
Figure 2.

Computational approaches to cell division and growth. (A) A popular implementation of cell division rule. The cell wall is represented as a polygon of vertices connected by edges. According to the shortest-distance rule (Errera, 1888), the cell is divided by identifying the shortest division plane cutting through the cell. To avoid conflict with existing vertices, the two ends of the division plane can be spread apart by a minimal threshold distance. Cell division splits the cell into two daughter cells yielding two new connected vertices in the cell wall. Often, the cell wall is “pinched” along the newly created vertices (Smith et al., 2006b). (B) Computational model of leaf shape development (adapted from Runions and Tsiantis, 2017). Mature leaf shape is achieved through the interaction between three components: a proximal-distal hypothetical morphogen and two master regulators. The basipetal red-orange-yellow gradient region defines the action of the growth morphogen (red: higher growth, yellow: lower growth), where the dashed line indicates the border between the actively growing region and the differentiation zone. The marginal patterning of the leaf blade is the result of the combined action of a local growth activator (red) and a growth suppressor (blue). (C) Computational model of radicle emergence (adapted from Marconi et al., 2021). This simulation reproduces the embryonic emergence of the root meristem of Arabidopsis. Organ growth follows the combined action of cell elongation, cell division, and tissue mechanics. Note that the organ maintains a distinct anisotropic form through the self-organization of cortical microtubules despite each single cell being expanded by uniform turgor pressure (see Marconi et al., 2021 for details).